2021-03-20 07:58:25 +00:00
|
|
|
|
## KMP算法(Knuth-Morris-Pratt)
|
|
|
|
|
|
|
2021-03-21 05:00:46 +00:00
|
|
|
|
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
|
|
|
|
|
>
|
|
|
|
|
|
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
|
|
|
|
|
>
|
|
|
|
|
|
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
|
|
|
|
|
|
2021-03-20 07:58:25 +00:00
|
|
|
|
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
|
|
|
|
|
|
|
|
|
|
|
|
我们先来看一个实例
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
|
|
|
|
|
|
|
|
|
|
|
|
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
|
|
|
|
|
|
|
|
|
|
|
|
在上面的例子中我们提到了一个名词,**最长公共前后缀**,这个是什么意思呢?下面我们通过一个较简单的例子进行描述。
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
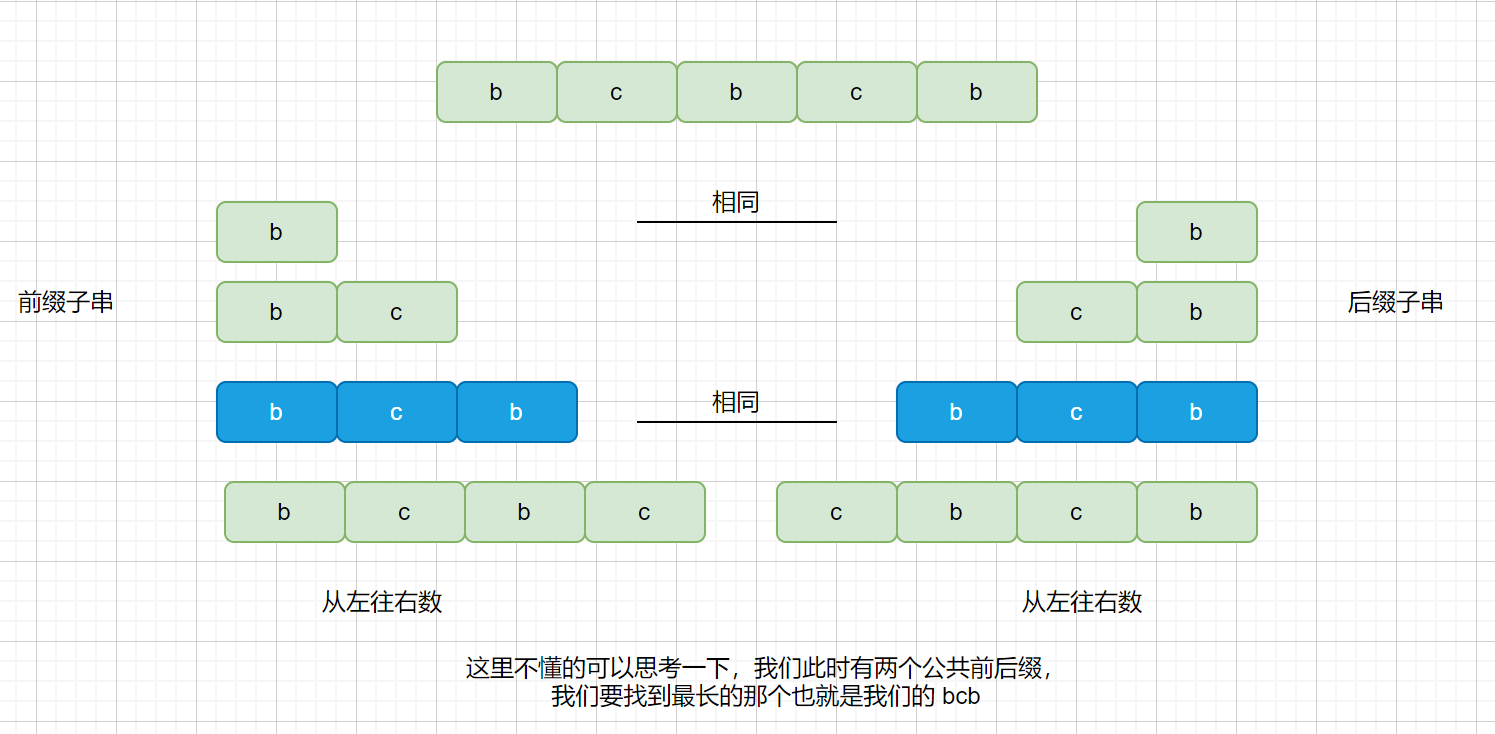
此时我们在红色阴影处匹配失败,绿色为匹配成功部分,则我们观察匹配成功的部分。
|
|
|
|
|
|
|
|
|
|
|
|
我们来看一下匹配成功部分的所有前缀
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
我们的最长公共前后缀如下图,则我们需要这样移动
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
|
|
|
|
|
|
|
|
|
|
|
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
|
|
|
|
|
|
|
|
|
|
|
|
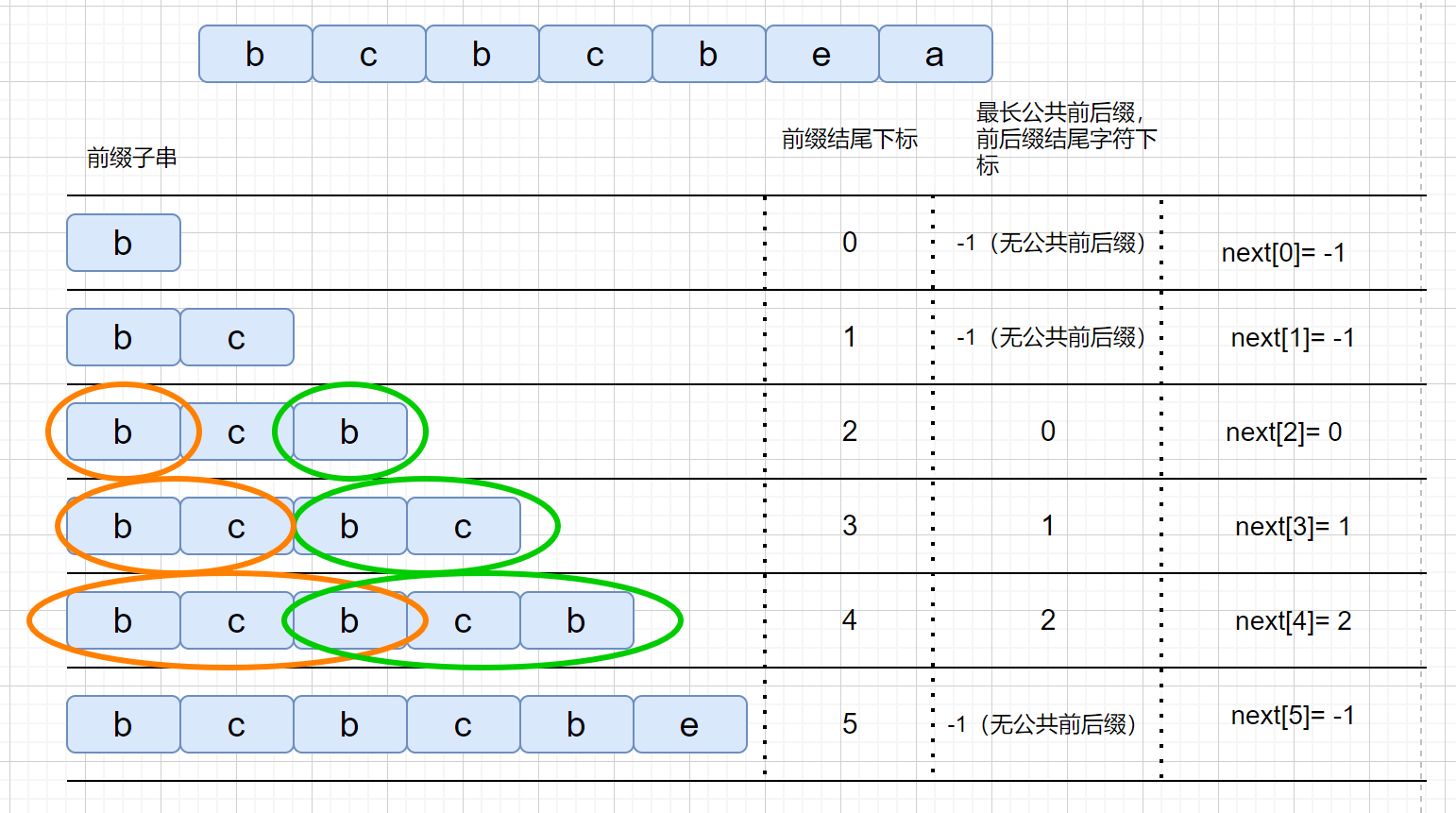
next 数组存的咱们最长公共前后缀中,前缀的结尾字符下标。是不是感觉有点别扭,我们通过一个例子进行说明。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
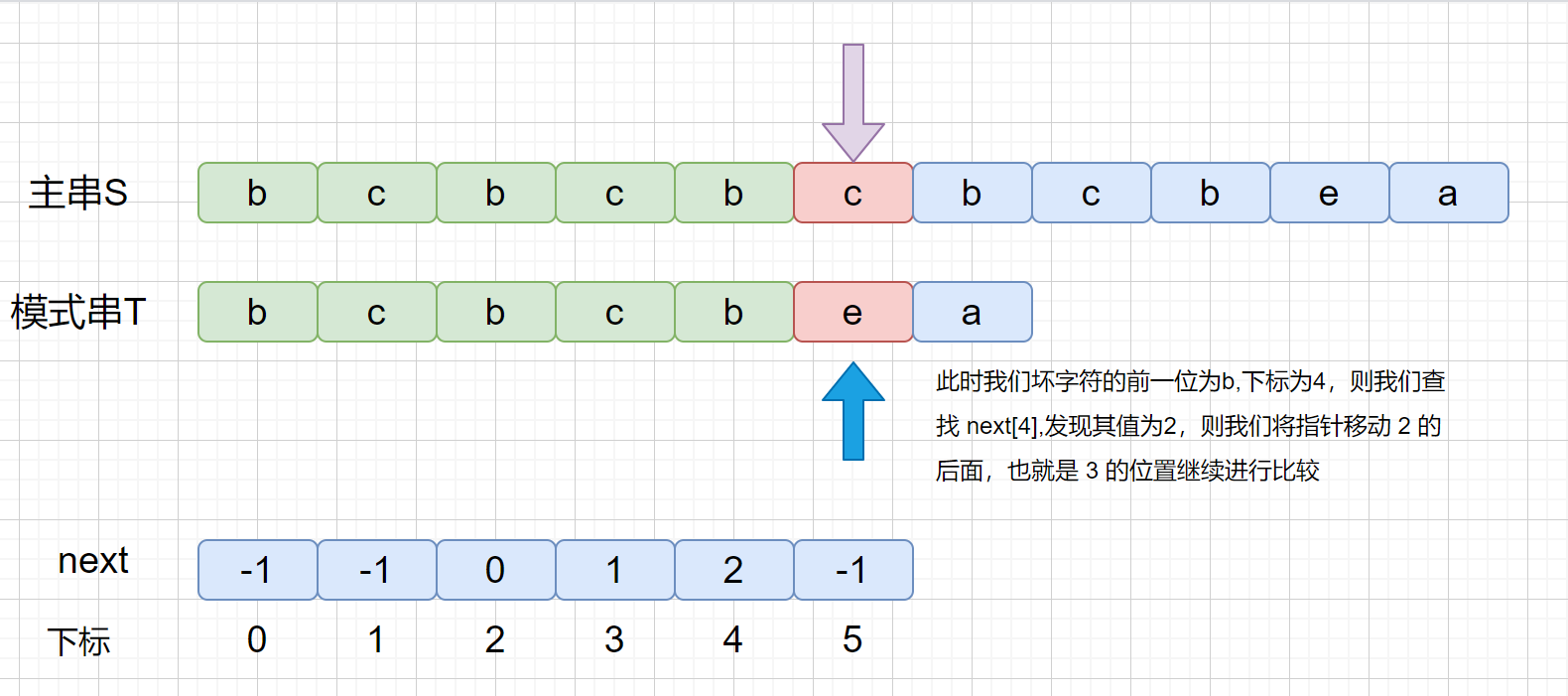
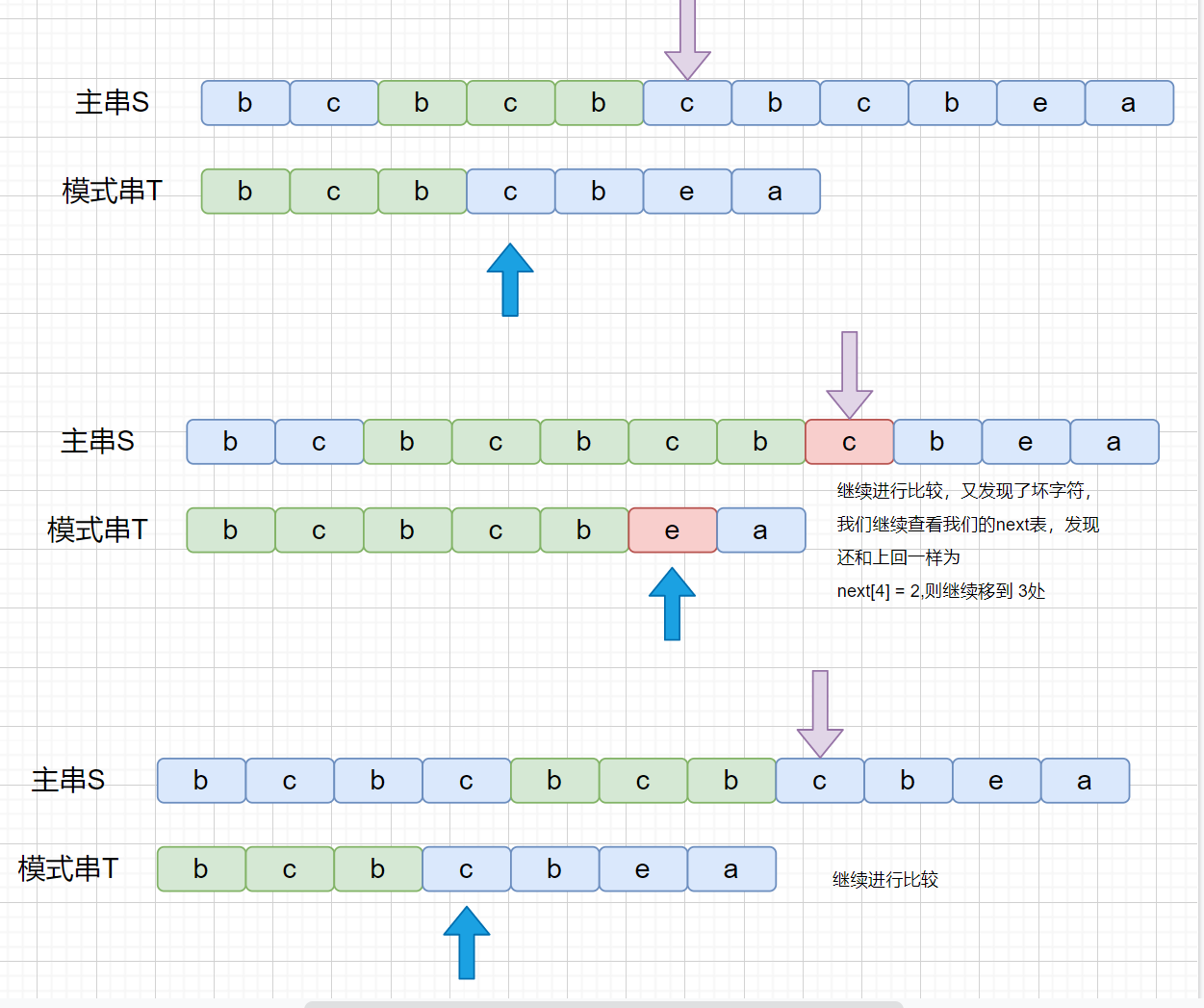
我们知道 next 数组之后,我们的 KMP 算法实现起来就很容易啦,另外我们看一下 next 数组到底是干什么用的。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
剩下的就不用说啦,完全一致啦,咱们将上面这个例子,翻译成和咱们开头对应的动画大家看一下。
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
下面我们看一下代码,标有详细注释,大家认真看呀。
|
|
|
|
|
|
|
|
|
|
|
|
**注:很多教科书的 next 数组表示方式不一致,理解即可**
|
|
|
|
|
|
|
|
|
|
|
|
```java
|
|
|
|
|
|
class Solution {
|
|
|
|
|
|
public int strStr(String haystack, String needle) {
|
|
|
|
|
|
//两种特殊情况
|
|
|
|
|
|
if (needle.length() == 0) {
|
|
|
|
|
|
return 0;
|
|
|
|
|
|
}
|
|
|
|
|
|
if (haystack.length() == 0) {
|
|
|
|
|
|
return -1;
|
|
|
|
|
|
}
|
|
|
|
|
|
// char 数组
|
|
|
|
|
|
char[] hasyarr = haystack.toCharArray();
|
|
|
|
|
|
char[] nearr = needle.toCharArray();
|
|
|
|
|
|
//长度
|
|
|
|
|
|
int halen = hasyarr.length;
|
|
|
|
|
|
int nelen = nearr.length;
|
|
|
|
|
|
//返回下标
|
|
|
|
|
|
return kmp(hasyarr,halen,nearr,nelen);
|
|
|
|
|
|
|
|
|
|
|
|
}
|
|
|
|
|
|
public int kmp (char[] hasyarr, int halen, char[] nearr, int nelen) {
|
|
|
|
|
|
//获取next 数组
|
|
|
|
|
|
int[] next = next(nearr,nelen);
|
|
|
|
|
|
int j = 0;
|
|
|
|
|
|
for (int i = 0; i < halen; ++i) {
|
|
|
|
|
|
//发现不匹配的字符,然后根据 next 数组移动指针,移动到最大公共前后缀的,
|
|
|
|
|
|
//前缀的后一位,和咱们移动模式串的含义相同
|
|
|
|
|
|
while (j > 0 && hasyarr[i] != nearr[j]) {
|
|
|
|
|
|
j = next[j - 1] + 1;
|
|
|
|
|
|
//超出长度时,可以直接返回不存在
|
|
|
|
|
|
if (nelen - j + i > halen) {
|
|
|
|
|
|
return -1;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
//如果相同就将指针同时后移一下,比较下个字符
|
|
|
|
|
|
if (hasyarr[i] == nearr[j]) {
|
|
|
|
|
|
++j;
|
|
|
|
|
|
}
|
|
|
|
|
|
//遍历完整个模式串,返回模式串的起点下标
|
|
|
|
|
|
if (j == nelen) {
|
|
|
|
|
|
return i - nelen + 1;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
return -1;
|
|
|
|
|
|
}
|
|
|
|
|
|
//这一块比较难懂,不想看的同学可以忽略,了解大致含义即可,或者自己调试一下,看看运行情况
|
|
|
|
|
|
//我会每一步都写上注释
|
|
|
|
|
|
public int[] next (char[] needle,int len) {
|
|
|
|
|
|
//定义 next 数组
|
|
|
|
|
|
int[] next = new int[len];
|
|
|
|
|
|
// 初始化
|
|
|
|
|
|
next[0] = -1;
|
|
|
|
|
|
int k = -1;
|
|
|
|
|
|
for (int i = 1; i < len; ++i) {
|
|
|
|
|
|
//我们此时知道了 [0,i-1]的最长前后缀,但是k+1的指向的值和i不相同时,我们则需要回溯
|
|
|
|
|
|
//因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标(即长度)
|
|
|
|
|
|
//就要找 k+1前一个元素在next数组里的值,即next[k+1]
|
|
|
|
|
|
while (k != -1 && needle[k + 1] != needle[i]) {
|
|
|
|
|
|
k = next[k];
|
|
|
|
|
|
}
|
|
|
|
|
|
// 相同情况,就是 k的下一位,和 i 相同时,此时我们已经知道 [0,i-1]的最长前后缀
|
|
|
|
|
|
//然后 k - 1 又和 i 相同,最长前后缀加1,即可
|
|
|
|
|
|
if (needle[k+1] == needle[i]) {
|
|
|
|
|
|
++k;
|
|
|
|
|
|
}
|
|
|
|
|
|
next[i] = k;
|
|
|
|
|
|
|
|
|
|
|
|
}
|
|
|
|
|
|
return next;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|