algorithm-base/animation-simulation/二叉树/二叉树中序遍历（迭代）.md

哈喽大家好，我是厨子，之前我们说了二叉树前序遍历的迭代法和 Morris，今天咱们写一下中序遍历的迭代法和 Morris。

> 注：数据结构掌握不熟练的同学，阅读该文章之前，可以先阅读这两篇文章，二叉树基础，前序遍历另外喜欢电脑阅读的同学，可以在小屋后台回复仓库地址，获取 Github 链接进行阅读。

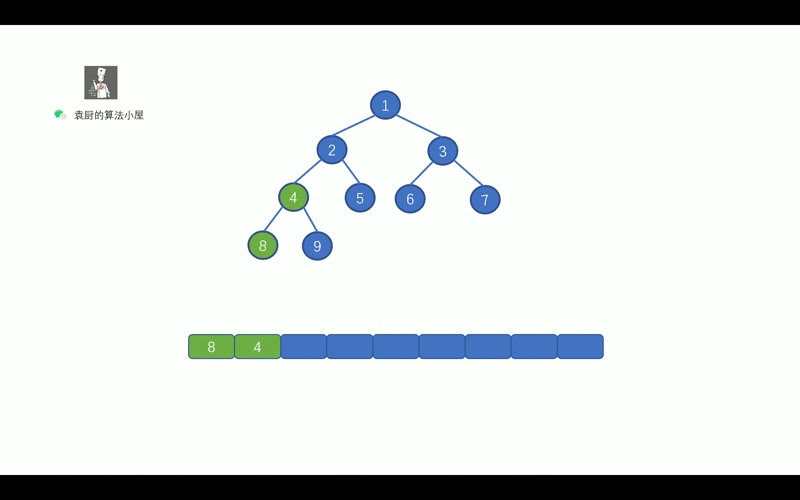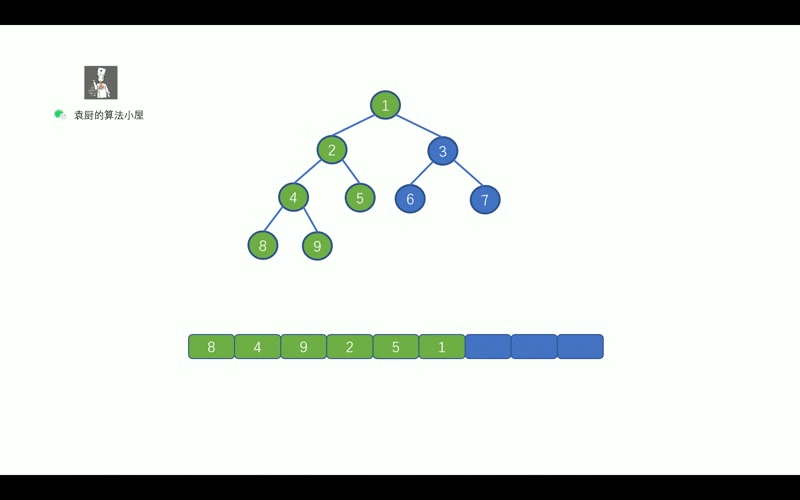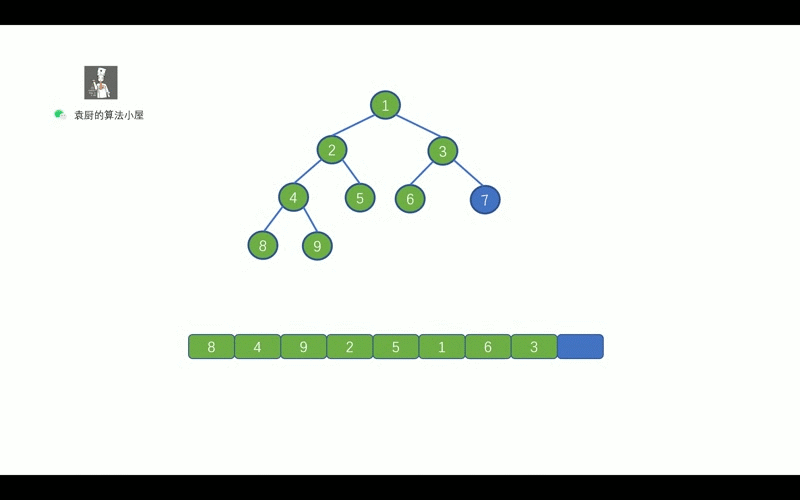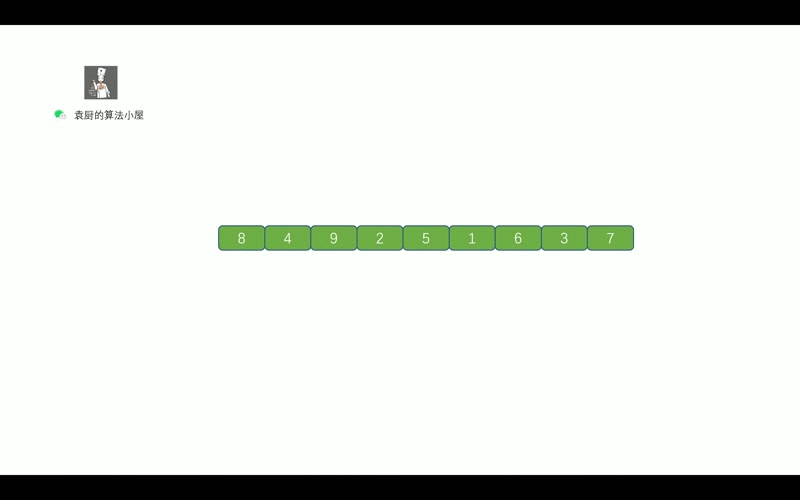
中序遍历的顺序是, `对于树中的某节点,先遍历该节点的左子树, 然后再遍历该节点, 最后遍历其右子树`。老规矩，上动画，我们先通过动画回忆一下二叉树的中序遍历。

![中序遍历](https://cdn.jsdelivr.net/gh/tan45du/test@master/photo/中序遍历.7gct7ztck8k0.gif)

注：二叉树基础总结大家可以阅读这篇文章，点我。

## 迭代法

我们二叉树的中序遍历迭代法和前序遍历是一样的，都是借助栈来帮助我们完成。

我们结合动画思考一下，该如何借助栈来实现呢？

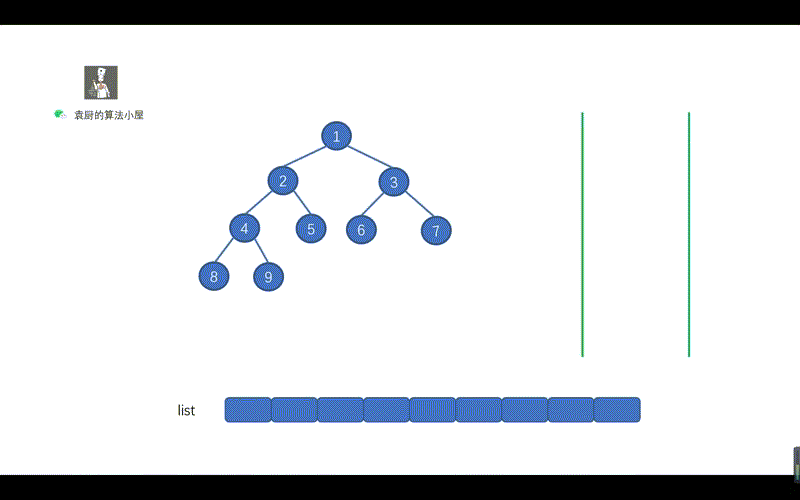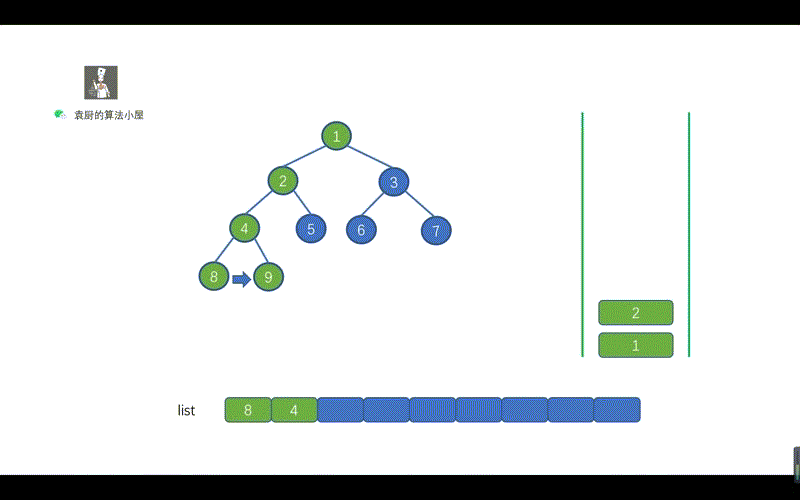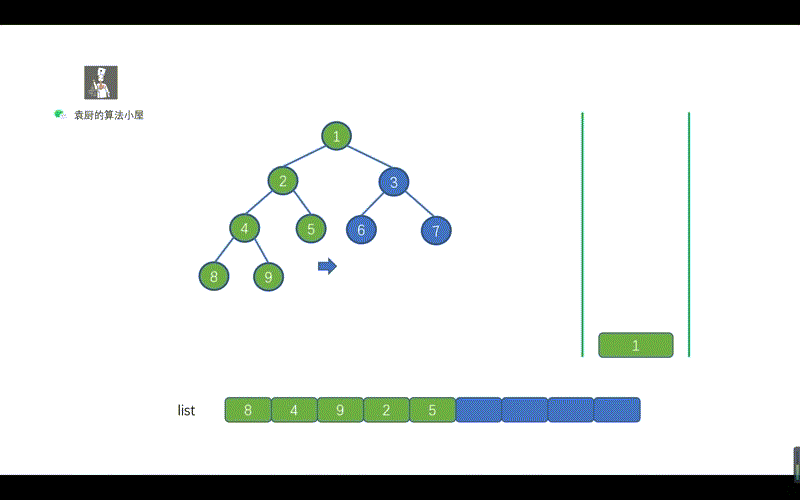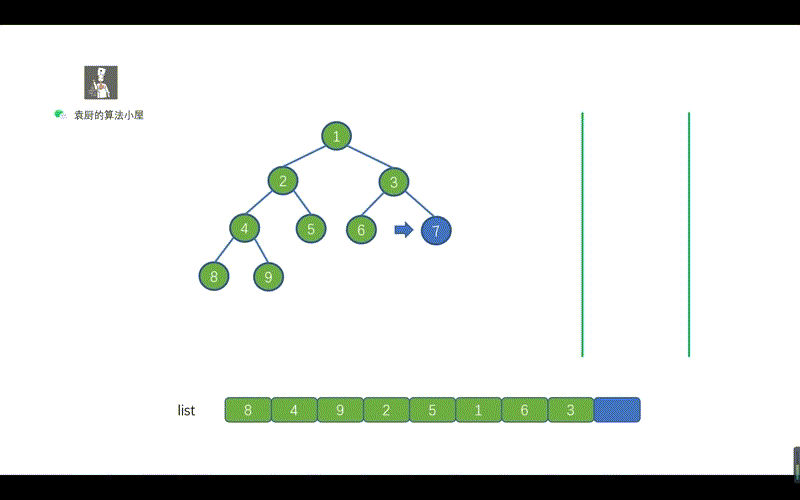
我们来看下面这个动画。

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210608010104232.gif)

用栈实现的二叉树的中序遍历有两个关键的地方。

- 指针不断向节点的左孩子移动，为了找到我们当前需要遍历的节点。途中不断执行入栈操作
- 当指针为空时，则开始出栈，并将指针指向出栈节点的右孩子。

这两个关键点也很容易理解，指针不断向左孩子移动，是为了找到我们此时需要节点。然后当指针指向空时，则说明我们此时已经找到该节点，执行出栈操作，并将其值存入 list 即可，另外我们需要将指针指向出栈节点的右孩子，迭代执行上诉操作。

大家是不是已经知道怎么写啦，下面我们看代码吧。

```java
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> arr = new ArrayList<>();
        TreeNode cur = new TreeNode(-1);
        cur = root;
        Stack<TreeNode> stack = new Stack<>();
        while (!stack.isEmpty() || cur != null) {   
               //找到当前应该遍历的那个节点
               while (cur != null) {
                 stack.push(cur);
                 cur = cur.left;
               }
               //此时指针指向空，也就是没有左子节点，则开始执行出栈操作
               TreeNode temp = stack.pop();
               arr.add(temp.val);
               //指向右子节点
               cur = temp.right;
        }
        return arr;
    } 
}
```

Swift Code：

```swift
class Solution {
    func inorderTraversal(_ root: TreeNode?) -> [Int] {
        var arr:[Int] = []
        var cur = root
        var stack:[TreeNode] = []

        while !stack.isEmpty || cur != nil {
            //找到当前应该遍历的那个节点
            while cur != nil {
                stack.append(cur!)
                cur = cur!.left
            }
            //此时指针指向空，也就是没有左子节点，则开始执行出栈操作
            if let temp = stack.popLast() {
                arr.append(temp.val)
                //指向右子节点
                cur = temp.right
            }
        }
        return arr
    }
}
```

Go Code:

```go
func inorderTraversal(root *TreeNode) []int {
    res := []int{}
    if root == nil {
        return res
    }
    stk := []*TreeNode{}
    cur := root
    for len(stk) != 0 || cur != nil {
        // 找到当前应该遍历的那个节点，并且把左子节点都入栈
        for cur != nil {
            stk = append(stk, cur)
            cur = cur.Left
        }
        // 没有左子节点，则开始执行出栈操作
        temp := stk[len(stk) - 1]
        stk = stk[: len(stk) - 1]
        res = append(res, temp.Val)
        cur = temp.Right
    }
    return res
}
```

###