mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-24 21:08:53 +00:00
204 lines
6.8 KiB
Markdown
204 lines
6.8 KiB
Markdown
|
|
之前我们说过了如何利用快速排序解决荷兰国旗问题,下面我们看下这两个题目
|
|||
|
|
|
|||
|
|
**剑指 Offer 45. 把数组排成最小的数**,**leetcode 179 最大数**
|
|||
|
|
|
|||
|
|
这两个问题根本上也是排序问题,下面我们一起来看一下题目描述
|
|||
|
|
|
|||
|
|
输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
|
|||
|
|
|
|||
|
|
示例 1:
|
|||
|
|
|
|||
|
|
> 输入: [10,2]
|
|||
|
|
> 输出: "102"
|
|||
|
|
|
|||
|
|
示例 2:
|
|||
|
|
|
|||
|
|
> 输入: [3,30,34,5,9]
|
|||
|
|
> 输出: "3033459"
|
|||
|
|
|
|||
|
|
题目很容易理解,就是让我们找出拼接的所有数字中最小的一个,但是我们需要注意的是,因为输出结果较大,所以我们不能返回 int 应该将数字转换成字符串,所以这类问题还是隐形的大数问题。
|
|||
|
|
|
|||
|
|
我们看到这个题目时,可能想到的是这种解题思路,我们首先求出数组中所有数字的全排列,然后将排列拼起来,最后再从中取出最小的值,但是我们共有 n 个数,则有 n !个排列,显然数目是十分庞大的,那么我们有没有其他更高效的方法呢?
|
|||
|
|
|
|||
|
|
大家先来思考一下这个问题。
|
|||
|
|
|
|||
|
|
我们假设两个数字 m , n 可以拼接成 mn 和 nm 那么我们怎么返回最小的那个数字呢?
|
|||
|
|
|
|||
|
|
我们需要比较 mn 和 nm ,假设 mn < nm 则此时我们求得的最小数字就是 mn
|
|||
|
|
|
|||
|
|
> 注:mn 代表 m 和 n 进行拼接,例如 m = 10, n = 1,mn = 101
|
|||
|
|
|
|||
|
|
当 mn < nm 时,得到最小数字 mn, 因为在最小数字 mn 中 ,m 排在 n 的前面,我们此时定义 m "小于" n。
|
|||
|
|
|
|||
|
|
**注意:此时的 "小于" ,并不是数值的 < 。是我们自己定义,因为 m 在最小数字 mn 中位于 n 的前面,所以我们定义 m 小于 n。**
|
|||
|
|
|
|||
|
|
下面我们通过一个例子来加深下理解。
|
|||
|
|
|
|||
|
|
假设 m = 10,n = 1 则有 mn = 101 和 nm = 110
|
|||
|
|
|
|||
|
|
我们比较 101 和 110 ,发现 101 < 110 所以此时我们的最小数字为 101 ,又因为在最小数字中 10 (m) 排在 1(n) 的前面,我们根据定义则是 10 “小于” 1,反之亦然。
|
|||
|
|
|
|||
|
|
这时我们自己定义了一种新的,比较两个数字大小的规则,但是我们怎么保证这种规则是有效的?
|
|||
|
|
|
|||
|
|
怎么能确保通过这种规则,拼接数组中**所有数字**(我们之前仅仅是通过两个数字进行举例),得到的数就是最小的数字呢?
|
|||
|
|
|
|||
|
|
下面我们先来证明下规则的有效性
|
|||
|
|
|
|||
|
|
注:为了便于分辨我们用 A,B,C 表示元素, a,b,c 表示元素用十进制表示时的位数
|
|||
|
|
|
|||
|
|
(1)自反性:AA = AA,所以 A 等于 A
|
|||
|
|
|
|||
|
|
(2)对称性:如果 A "小于" B 则 AB < BA,所以 BA > AB 则 B "大于" A
|
|||
|
|
|
|||
|
|
(3)传递性:传递性的证明稍微有点复杂,大家记得认真阅读。
|
|||
|
|
|
|||
|
|
如果 A“小于” B,则 AB < BA, 假设 A 和 B 用十进制表示时分别有 a 位和 b 位
|
|||
|
|
|
|||
|
|
则 AB = A * 10 ^ b + B , BA = B * 10 ^ a + A
|
|||
|
|
|
|||
|
|
> 例 A = 10, a = 2 (两位数) B = 1, b = 1 (一位数)
|
|||
|
|
>
|
|||
|
|
> AB = A * 10 ^ b + B = 10 * 10 ^ 1 + 1 = 101
|
|||
|
|
>
|
|||
|
|
> BA = B * 10 ^ a + A = 1 * 10 ^ 2 + 10 = 110
|
|||
|
|
|
|||
|
|
AB < BA 则 **A * 10 ^ b + B < BA = B * 10 ^ a + A** 整理得
|
|||
|
|
|
|||
|
|
A / (10^a - 1) < B / (10 ^ b - 1)
|
|||
|
|
|
|||
|
|
同理,如果 B “小于” C 则 BC < CB ,C 用十进制表示时有 c 位,和前面推导过程一样
|
|||
|
|
|
|||
|
|
BC = B * 10 ^ c + C
|
|||
|
|
|
|||
|
|
CB = C * 10 ^ b + B
|
|||
|
|
|
|||
|
|
BC < CB 整理得 B / (10 ^ b - 1) < C / (10 ^ c - 1);
|
|||
|
|
|
|||
|
|
我们通过 A / (10 ^ a - 1) < B / (10 ^ b - 1) ,B / (10 ^ b - 1) < C / (10 ^ c - 1);
|
|||
|
|
|
|||
|
|
可以得到 A / (10^a - 1) < C / (10 ^ c - 1)
|
|||
|
|
|
|||
|
|
则可以得到 AC < CA 即 A “小于” C
|
|||
|
|
|
|||
|
|
传递性证得。
|
|||
|
|
|
|||
|
|
我们通过上面的证明过程知道了我们定义的规则,满足自反性,对称性,传递性,则说明规则是有效的。
|
|||
|
|
|
|||
|
|
接下来我们证明,利用这种规则得到的数字,的确是最小的。我们利用反证法来进行证明
|
|||
|
|
|
|||
|
|
我们先来回顾一下我们之前定义的规则
|
|||
|
|
|
|||
|
|
> 当 mn < nm 时,得到最小数字 mn, 因为在最小数字 mn 中 ,m 排在 n 的前面,
|
|||
|
|
>
|
|||
|
|
> 我们此时定义 m "小于" n。
|
|||
|
|
|
|||
|
|
我们假设我们根据上诉规则得到的数字为 xxxxxxxx
|
|||
|
|
|
|||
|
|
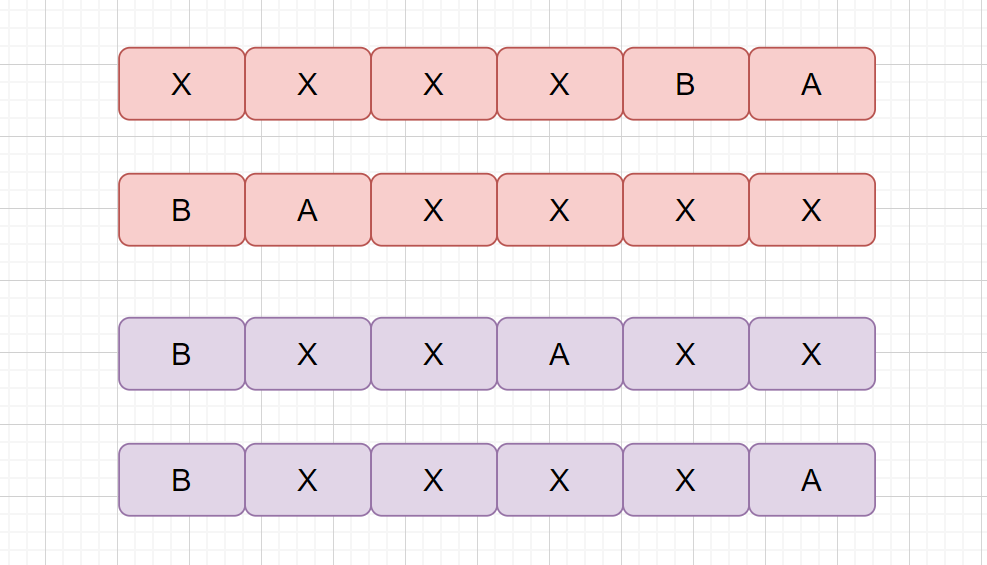
存在这么一对字符串 A B ,虽然 AB < BA, 按照规则 A 应该排在 B 的前面,但是在最后结果中 A 排在 B 的后面。则此时共有这么几种情况
|
|||
|
|
|
|||
|
|
见下图
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
其实我们可以归结为两大类, B 和 A 之间没有其他值, B 和 A 之间有其他值。
|
|||
|
|
|
|||
|
|
我们先来看**没有其他值**的情况
|
|||
|
|
|
|||
|
|
假设我们求得的最小值为 XXXXBA, 虽然 A "小于" B,但是在最后结果中 B 排在了 A 的前面,这和我们之前定义的规则是冲突的,大家思考一下这个值为最小值吗?
|
|||
|
|
|
|||
|
|
假设 XXXXBA为最小值,但是因为 A "小于" B ,则 AB < BA ,
|
|||
|
|
|
|||
|
|
所以 XXXXAB 一定小于 XXXXBA 。
|
|||
|
|
|
|||
|
|
和我们之前的假设矛盾。
|
|||
|
|
|
|||
|
|
当然 BAXXXX 也一样。
|
|||
|
|
|
|||
|
|
下面我们来看当 B 和 A 之间有其他值的情况
|
|||
|
|
|
|||
|
|
即 BXXXXA
|
|||
|
|
|
|||
|
|
我们可以将 XXXX 看成一个字符串 C,则为 BCA
|
|||
|
|
|
|||
|
|
因为求得的最小值为 BCA ,
|
|||
|
|
|
|||
|
|
在最小值 BCA 中 B 在 C 的前面,C 在 A 的前面,
|
|||
|
|
|
|||
|
|
则 BC < CB, CA < AC,B "小于 C", C “小于” A
|
|||
|
|
|
|||
|
|
根据我们之前证明的传递性
|
|||
|
|
|
|||
|
|
则 B "小于" A
|
|||
|
|
|
|||
|
|
但是我们假设是 A “小于” B ,与假设冲突,证得
|
|||
|
|
|
|||
|
|
综上所述,得出假设不成立,从而得出结论:对于排成的最小数字,不存在满足下述关系的一对字符串:虽然 A "小于" B , 但是在最后结果中 B 排在了 A 的前面.
|
|||
|
|
|
|||
|
|
好啦,我们证明我们定义的规则有效下面我们直接看代码吧。继续使用我们的三向切分来解决
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
class Solution {
|
|||
|
|
public String minNumber(int[] nums) {
|
|||
|
|
String[] arr = new String[nums.length];
|
|||
|
|
//解决大数问题,将数字转换为字符串
|
|||
|
|
for (int i = 0 ; i < nums.length; ++i) {
|
|||
|
|
arr[i] = String.valueOf(nums[i]);
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
quickSort(arr,0,arr.length-1);
|
|||
|
|
StringBuffer str = new StringBuffer();
|
|||
|
|
|
|||
|
|
for (String x : arr) {
|
|||
|
|
str.append(x);
|
|||
|
|
}
|
|||
|
|
return str.toString();
|
|||
|
|
}
|
|||
|
|
public void quickSort(String[] arr, int left, int right) {
|
|||
|
|
if (left >= right) {
|
|||
|
|
return;
|
|||
|
|
}
|
|||
|
|
int low = left;
|
|||
|
|
int hight = right;
|
|||
|
|
int i = low+1;
|
|||
|
|
String pivot = arr[low];
|
|||
|
|
|
|||
|
|
while (i <= hight) {
|
|||
|
|
//比较大小
|
|||
|
|
if ((pivot+arr[i]).compareTo(arr[i]+pivot) > 0 ) {
|
|||
|
|
swap(arr,i++,low++);
|
|||
|
|
} else if ((pivot+arr[i]).compareTo(arr[i]+pivot) < 0) {
|
|||
|
|
swap(arr,i,hight--);
|
|||
|
|
} else {
|
|||
|
|
i++;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
quickSort(arr,left,low-1);
|
|||
|
|
quickSort(arr,hight+1,right);
|
|||
|
|
|
|||
|
|
}
|
|||
|
|
public void swap(String[] arr, int i, int j) {
|
|||
|
|
String temp = arr[i];
|
|||
|
|
arr[i] = arr[j];
|
|||
|
|
arr[j] = temp;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|