mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-16 17:13:39 +00:00
179 lines
8.8 KiB
Markdown
179 lines
8.8 KiB
Markdown
|
|
### **归并排序**
|
|||
|
|
|
|||
|
|
归并排序是必须要掌握的排序算法,也算是面试高频考点,下面我们就一起来扒一扒归并排序吧,原理很简单,大家一下就能搞懂。
|
|||
|
|
|
|||
|
|
袁记菜馆内
|
|||
|
|
|
|||
|
|
第 23 届食神争霸赛开赛啦!
|
|||
|
|
|
|||
|
|
袁厨想在自己排名前4的分店中,挑选一个最优秀的厨师来参加食神争霸赛,选拔规则如下。
|
|||
|
|
|
|||
|
|
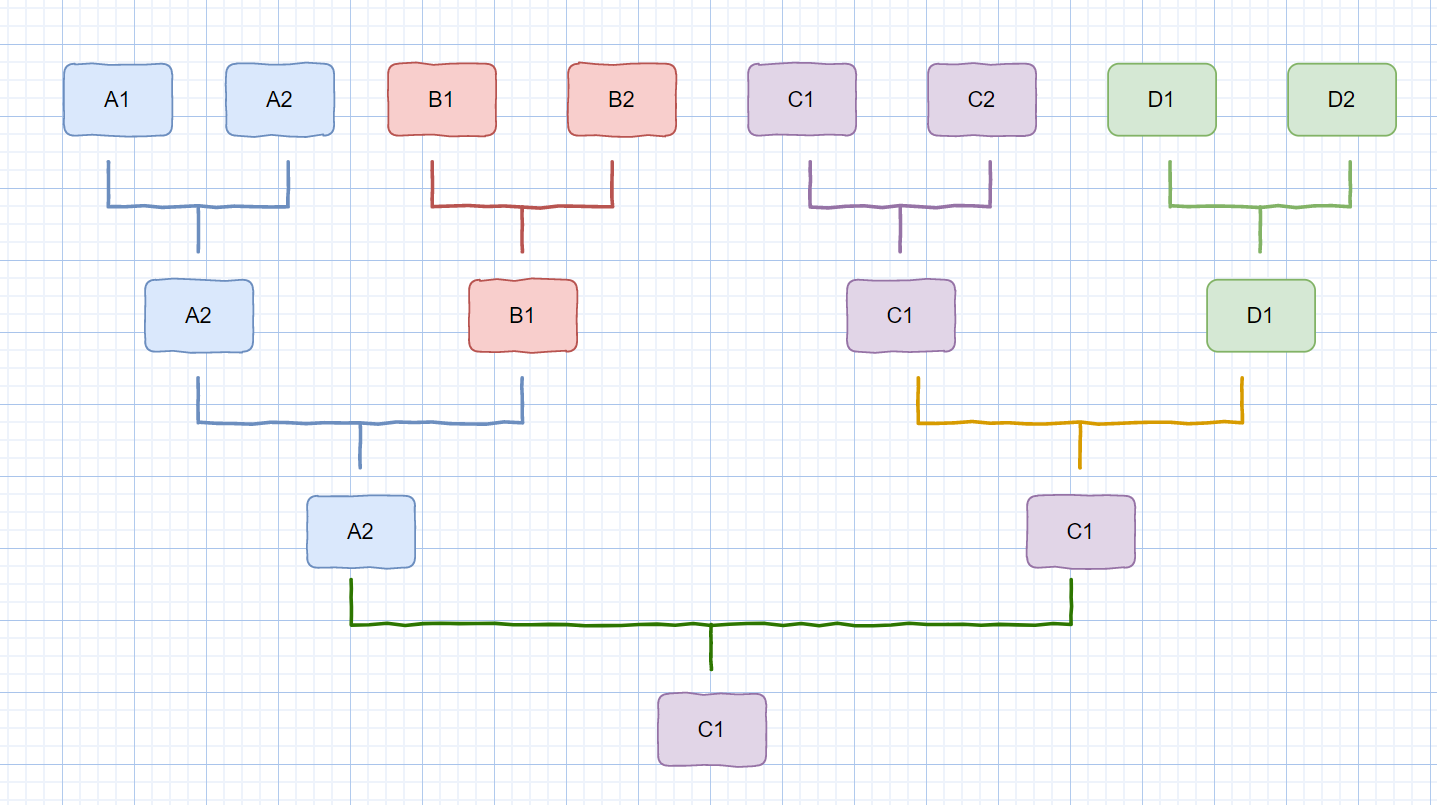
第一场 PK:每个分店选出两名厨师,首先进行店内 PK,选出店内里的胜者
|
|||
|
|
|
|||
|
|
第二场 PK: 然后店内的优胜者代表分店挑战其他某一分店的胜者(半决赛)
|
|||
|
|
|
|||
|
|
第三场 PK:最后剩下的两名胜者进行PK,选出最后的胜者。
|
|||
|
|
|
|||
|
|
示意图如下
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
上面的例子大家应该不会陌生吧,其实我们归并排序和食神选拔赛的流程是有些相似的,下面我们一起来看一下吧
|
|||
|
|
|
|||
|
|
归并这个词语的含义就是合并,并入的意思,而在我们的数据结构中的定义是将**两个或两个以上的有序表和成一个新的有序表**。而我们这里说的归并排序就是使用归并的思想实现的排序方法。
|
|||
|
|
|
|||
|
|
归并排序使用的就是分治思想。顾名思义就是分而治之,将一个大问题分解成若干个小的子问题来解决。小的子问题解决了,大问题也就解决了。分治后面会专门写一篇文章进行描述滴,这里先简单提一下。
|
|||
|
|
|
|||
|
|
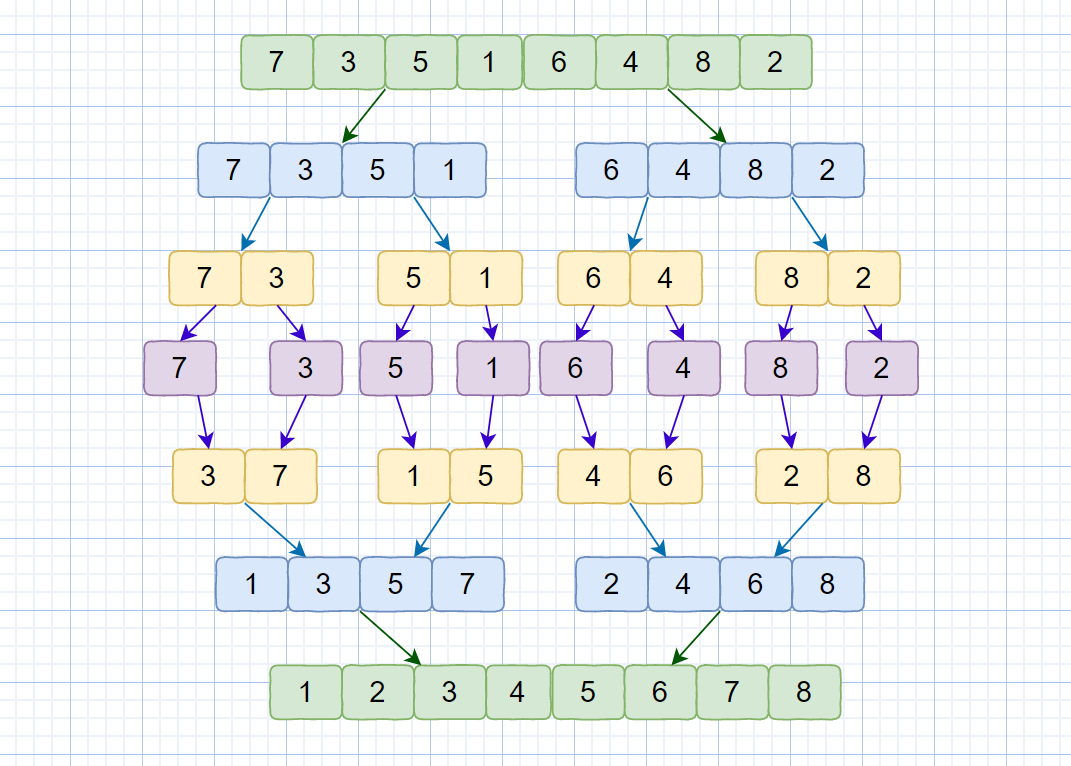
下面我们通过一个图片来描述一下归并排序的数据变换情况,见下图。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
我们简单了解了归并排序的思想,从上面的描述中,我们可以知道算法的归并过程是比较难实现的,这也是这个算法的重点,看完我们这个视频就能懂个大概啦。
|
|||
|
|
|
|||
|
|
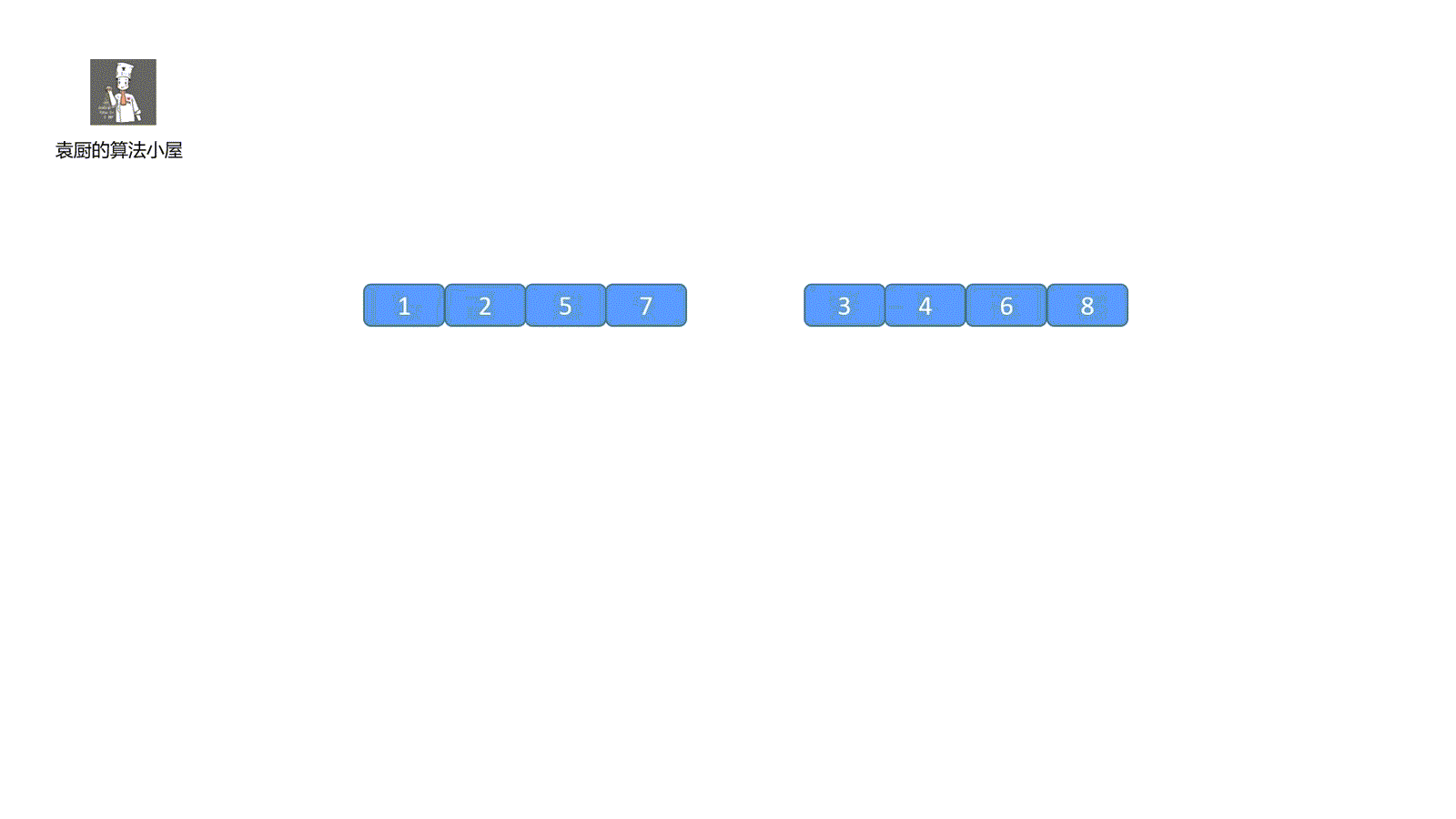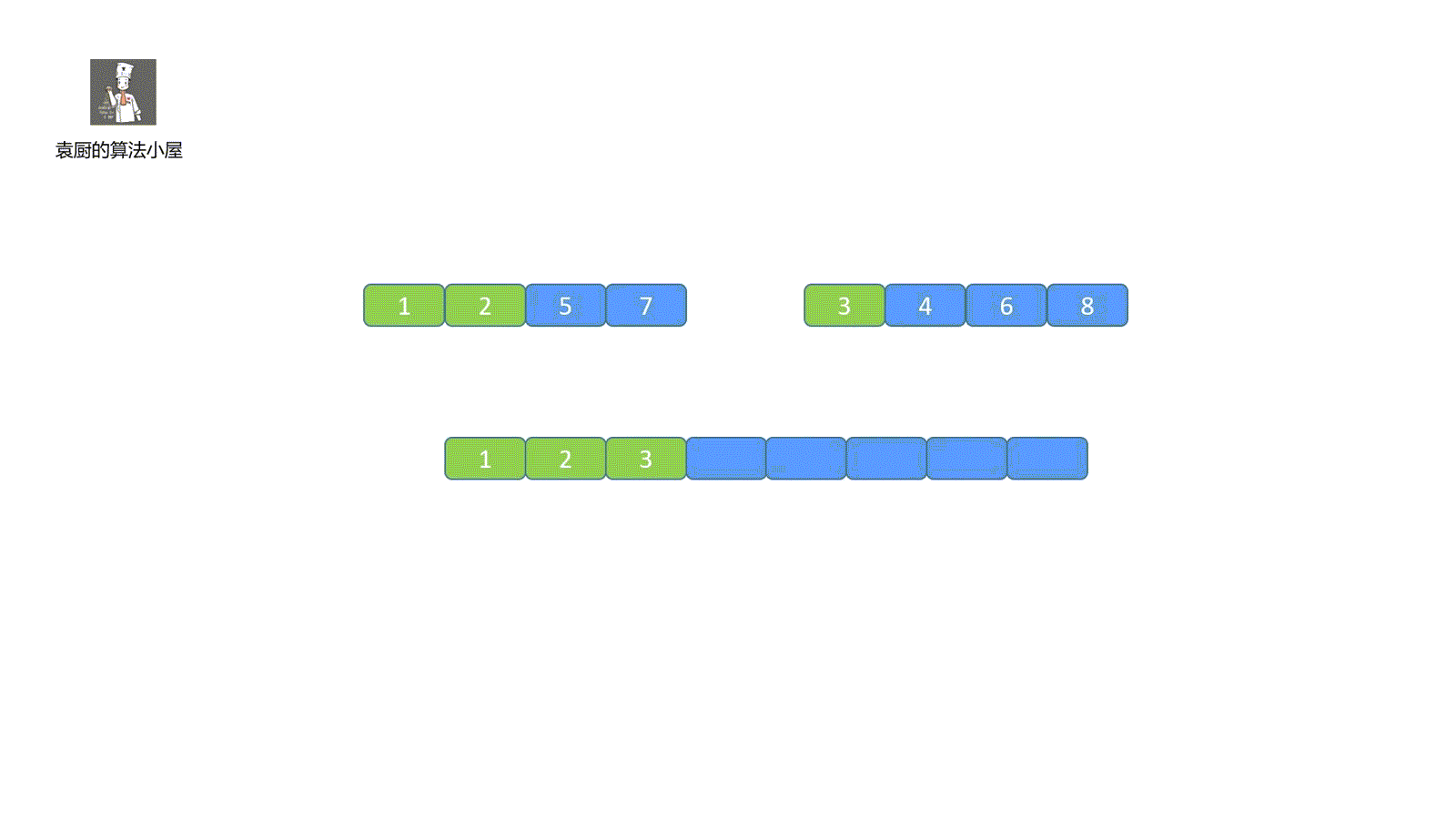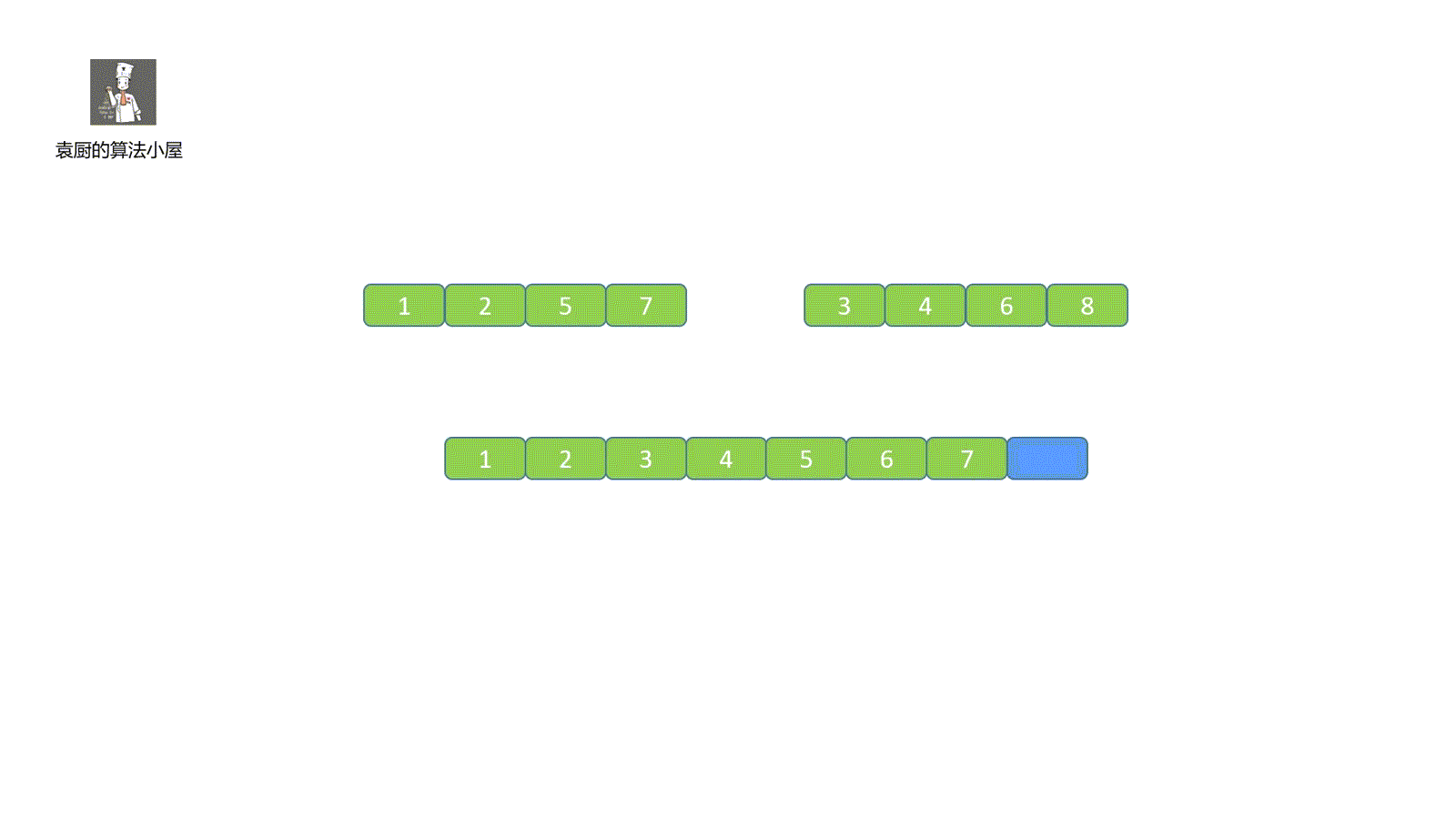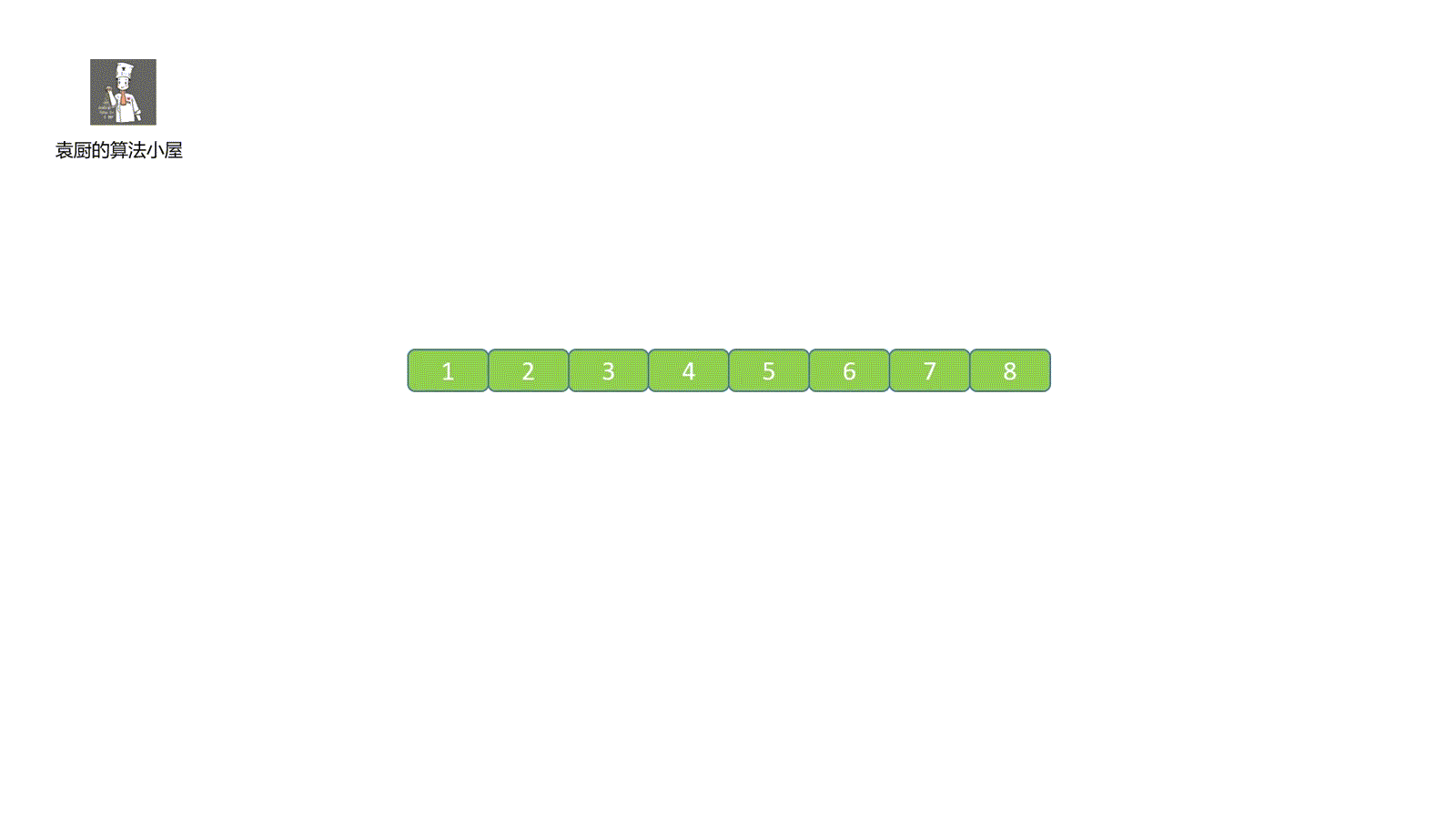
|
|||
|
|
|
|||
|
|
视频中归并步骤大家有没有看懂呀,没看懂也不用着急,下面我们一起来拆解一下,归并共有三步走。
|
|||
|
|
|
|||
|
|
第一步:创建一个额外大集合用于存储归并结果,长度则为那两个小集合的和,从视频中也可以看的出
|
|||
|
|
|
|||
|
|
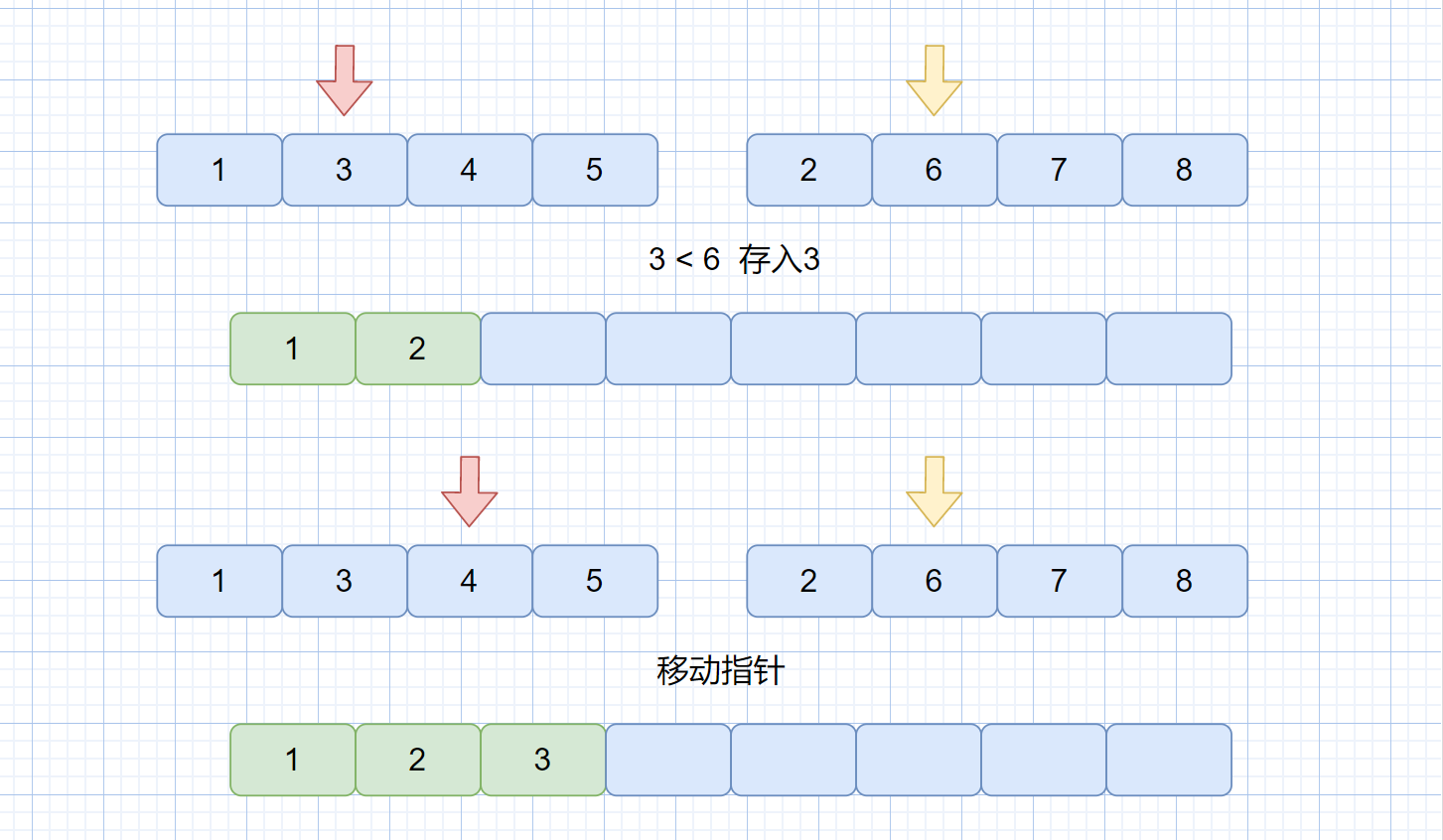
第二步:我们从左自右比较两个指针指向的值,将较小的那个存入大集合中,存入之后指针移动,并继续比较,直到某一小集合的元素全部都存到大集合中。见下图
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
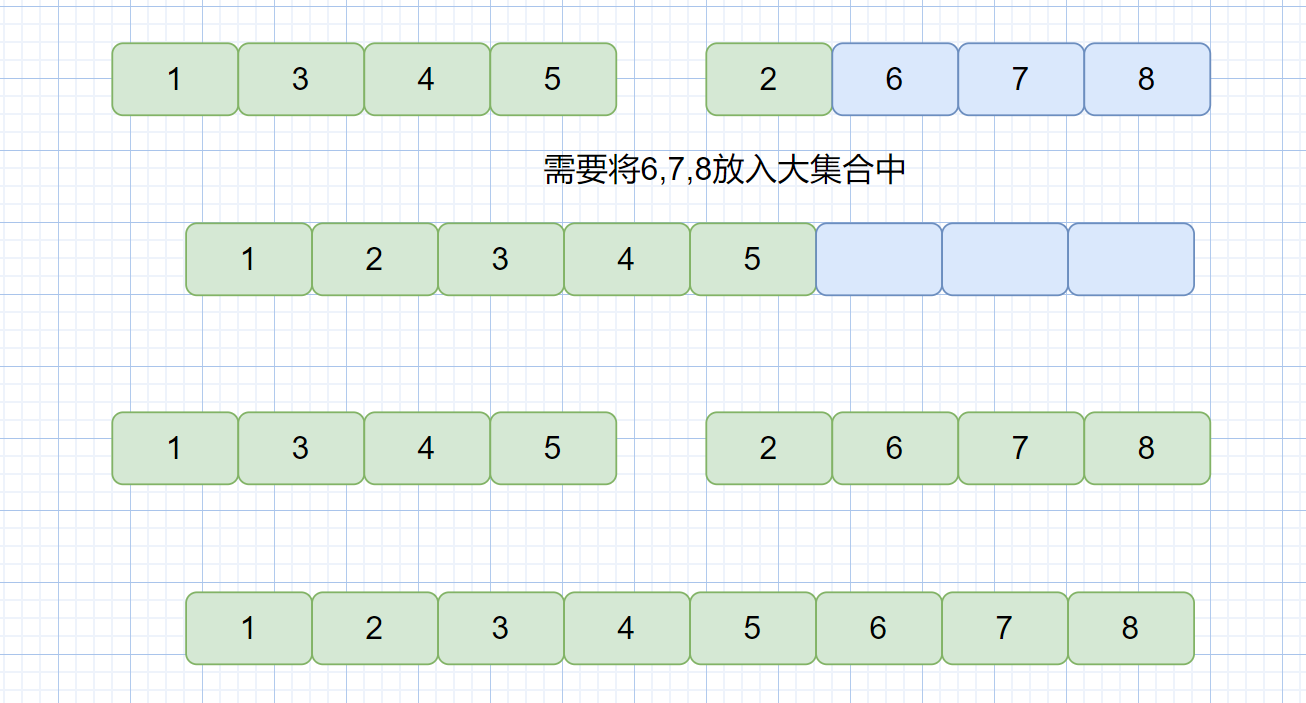
第三步:当某一小集合元素全部放入大集合中,则需将另一小集合中剩余的所有元素存到大集合中,见下图
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
好啦,看完视频和图解是不是能够写出个大概啦,了解了算法原理之后代码写起来就很简单啦,
|
|||
|
|
|
|||
|
|
下面我们看代码吧。
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
class Solution {
|
|||
|
|
public int[] sortArray(int[] nums) {
|
|||
|
|
mergeSort(nums,0,nums.length-1);
|
|||
|
|
return nums;
|
|||
|
|
}
|
|||
|
|
public void mergeSort(int[] arr, int left, int right) {
|
|||
|
|
if (left < right) {
|
|||
|
|
int mid = left + ((right - left) >> 1);
|
|||
|
|
mergeSort(arr,left,mid);
|
|||
|
|
mergeSort(arr,mid+1,right);
|
|||
|
|
merge(arr,left,mid,right);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
//归并
|
|||
|
|
public void merge(int[] arr,int left, int mid, int right) {
|
|||
|
|
//第一步,定义一个新的临时数组
|
|||
|
|
int[] temparr = new int[right -left + 1];
|
|||
|
|
int temp1 = left, temp2 = mid + 1;
|
|||
|
|
int index = 0;
|
|||
|
|
//对应第二步,比较每个指针指向的值,小的存入大集合
|
|||
|
|
while (temp1 <= mid && temp2 <= right) {
|
|||
|
|
if (arr[temp1] <= arr[temp2]) {
|
|||
|
|
temparr[index++] = arr[temp1++];
|
|||
|
|
} else {
|
|||
|
|
temparr[index++] = arr[temp2++];
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
//对应第三步,将某一小集合的剩余元素存到大集合中
|
|||
|
|
if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
|
|||
|
|
if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1); //将大集合的元素复制回原数组
|
|||
|
|
System.arraycopy(temparr,0,arr,0+left,right-left+1);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
**归并排序时间复杂度分析**
|
|||
|
|
|
|||
|
|
我们一趟归并,需要将两个小集合的长度放到大集合中,则需要将待排序序列中的所有记录扫描一遍所以时间复杂度为O(n)。归并排序把集合一层一层的折半分组,则由完全二叉树的深度可知,整个排序过程需要进行 logn(向上取整)次,则总的时间复杂度为 O(nlogn)。另外归并排序的执行效率与要排序的原始数组的有序程度无关,所以在最好,最坏,平均情况下时间复杂度均为 O(nlogn) 。虽然归并排序时间复杂度很稳定,但是他的应用范围却不如快速排序广泛,这是因为归并排序不是原地排序算法,空间复杂度不为 O(1),那么他的空间复杂度为多少呢?
|
|||
|
|
|
|||
|
|
**归并排序的空间复杂度分析**
|
|||
|
|
|
|||
|
|
归并排序所创建的临时结合都会在方法结束时释放,单次归并排序的最大空间是 n ,所以归并排序的空间复杂度为 O(n).
|
|||
|
|
|
|||
|
|
**归并排序的稳定性分析**
|
|||
|
|
|
|||
|
|
归并排序的稳定性,要看我们的 merge 函数,我们代码中设置了 arr[temp1] <= arr[temp2] ,当两个元素相同时,先放入arr[temp1] 的值到大集合中,所以两个相同元素的相对位置没有发生改变,所以归并排序是稳定的排序算法。
|
|||
|
|
|
|||
|
|
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|
|||
|
|
| -------- | -------------- | -------------- | -------------- | ---------- | -------- |
|
|||
|
|
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
|
|||
|
|
|
|||
|
|
等等还没完嘞,不要走。
|
|||
|
|
|
|||
|
|
归并排序的递归实现是比较常见的,也是比较容易理解的,下面我们一起来扒一下归并排序的迭代写法。看看他是怎么实现的。
|
|||
|
|
|
|||
|
|
我们通过一个视频来了解下迭代方法的思想,
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
是不是通过视频了解个大概啦,下面我们来对视频进行解析。
|
|||
|
|
|
|||
|
|
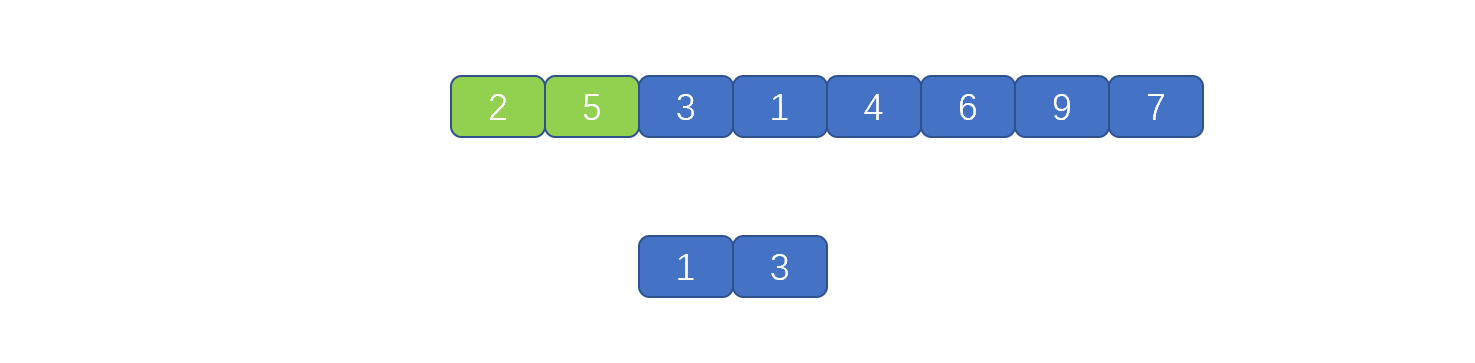
迭代实现的归并排序是将小集合合成大集合,小集合大小为 1,2,4,8,.....。依次迭代,见下图
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
比如此时小集合大小为 1 。两个小集合分别为 [3],[1]。然后我们根据合并规则,见第一个视频,将[3],[1]合并到临时数组中,则小的先进,则实现了排序,然后再将临时数组的元素复制到原来数组中。则实现了一次合并。
|
|||
|
|
|
|||
|
|
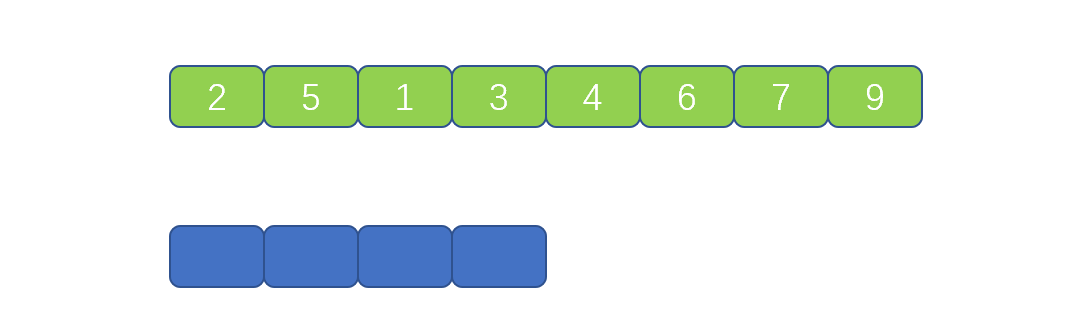
下面则继续合并[4],[6]。具体步骤一致。所有的小集合合并完成后,则小集合的大小变为 2,继续执行刚才步骤,见下图。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
此时子集合的大小为 2 ,则为 [2,5],[1,3] 继续按照上面的规则合并到临时数组中完成排序。 这就是迭代法的具体执行过程,
|
|||
|
|
|
|||
|
|
下面我们直接看代码吧。
|
|||
|
|
|
|||
|
|
注:递归法和迭代法的 merge函数代码一样。
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
class Solution {
|
|||
|
|
public int[] sortArray (int[] nums) {
|
|||
|
|
//代表子集合大小,1,2,4,8,16.....
|
|||
|
|
int k = 1;
|
|||
|
|
int len = nums.length;
|
|||
|
|
while (k < len) {
|
|||
|
|
mergePass(nums,k,len);
|
|||
|
|
k *= 2;
|
|||
|
|
}
|
|||
|
|
return nums;
|
|||
|
|
|
|||
|
|
}
|
|||
|
|
public void mergePass (int[] array, int k, int len) {
|
|||
|
|
|
|||
|
|
int i;
|
|||
|
|
for (i = 0; i < len-2*k; i += 2*k) {
|
|||
|
|
//归并
|
|||
|
|
merge(array,i,i+k-1,i+2*k-1);
|
|||
|
|
}
|
|||
|
|
//归并最后两个序列
|
|||
|
|
if (i + k < len) {
|
|||
|
|
merge(array,i,i+k-1,len-1);
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
}
|
|||
|
|
public void merge (int[] arr,int left, int mid, int right) {
|
|||
|
|
//第一步,定义一个新的临时数组
|
|||
|
|
int[] temparr = new int[right -left + 1];
|
|||
|
|
int temp1 = left, temp2 = mid + 1;
|
|||
|
|
int index = 0;
|
|||
|
|
//对应第二步,比较每个指针指向的值,小的存入大集合
|
|||
|
|
while (temp1 <= mid && temp2 <= right) {
|
|||
|
|
if (arr[temp1] <= arr[temp2]) {
|
|||
|
|
temparr[index++] = arr[temp1++];
|
|||
|
|
} else {
|
|||
|
|
temparr[index++] = arr[temp2++];
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
//对应第三步,将某一小集合的剩余元素存到大集合中
|
|||
|
|
if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
|
|||
|
|
if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);
|
|||
|
|
//将大集合的元素复制回原数组
|
|||
|
|
System.arraycopy(temparr,0,arr,0+left,right-left+1);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|