algorithm-base/gif-algorithm/二分查找及其变种/leetcode34查找第一个位置和最后一个位置.md

## 查找元素第一个位置和最后一个位置

上面我们说了如何使用二分查找在数组或区间里查出特定值的索引位置。但是我们刚才数组里面都没有重复值，查到返回即可，那么我们思考一下下面这种情况

![二分查找变种一](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/二分查找变种一.3axfe8rq0ei0.png)



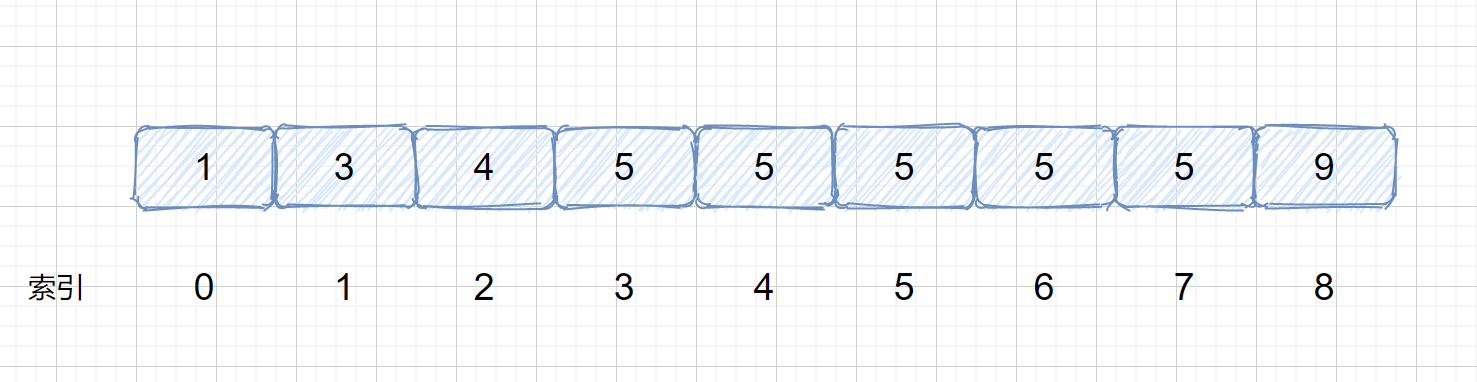
此时我们数组里含有多个 5 ，我们查询是否含有 5 可以很容易查到，但是我们想获取第一个 5 和 最后一个 5 的位置应该怎么实现呢？哦！我们可以使用遍历，当查询到第一个 5 时，我们设立一个指针进行定位，然后到达最后一个 5 时返回，这样我们就能求的第一个和最后一个五了？因为我们这个文章的主题就是二分查找，我们可不可以用二分查找来实现呢？当然是可以的。

### leetcode 34在排序数组中查找元素的第一个和最后一个位置

#### 题目描述

> 给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
>
> 如果数组中不存在目标值 target，返回 [-1, -1]。


示例 1：

> 输入：nums = [5,7,7,8,8,10], target = 8
> 输出：[3,4]

示例 2：

> 输入：nums = [5,7,7,8,8,10], target = 6
> 输出：[-1,-1]

示例 3：

> 输入：nums = [], target = 0
> 输出：[-1,-1]

#### 题目解析

这个题目很容易理解，我们在上面说了如何使用遍历解决该题，但是这个题目的目的就是让我们使用二分查找，我们来逐个分析，先找出目标元素的下边界，那么我们如何找到目标元素的下边界呢？

我们来重点分析一下刚才二分查找中的这段代码

```java
  if (nums[mid] == target) {
       return mid;
  }else if (nums[mid] < target) {
      //这里需要注意，移动左指针
      left  = mid + 1;
  }else if (nums[mid] > target) {
      //这里需要注意，移动右指针
      right = mid - 1;
  } 
```

我们只需在这段代码中修改即可，我们再来剖析一下这块代码，nums[mid] == target 时则返回，nums[mid] < target 时则移动左指针，在右区间进行查找， nums[mid]  >  target时则移动右指针，在左区间内进行查找。

那么我们思考一下，如果此时我们的 nums[mid] = target ,但是我们不能确定 mid 是否为该目标数的左边界，所以此时我们不可以返回下标。例如下面这种情况。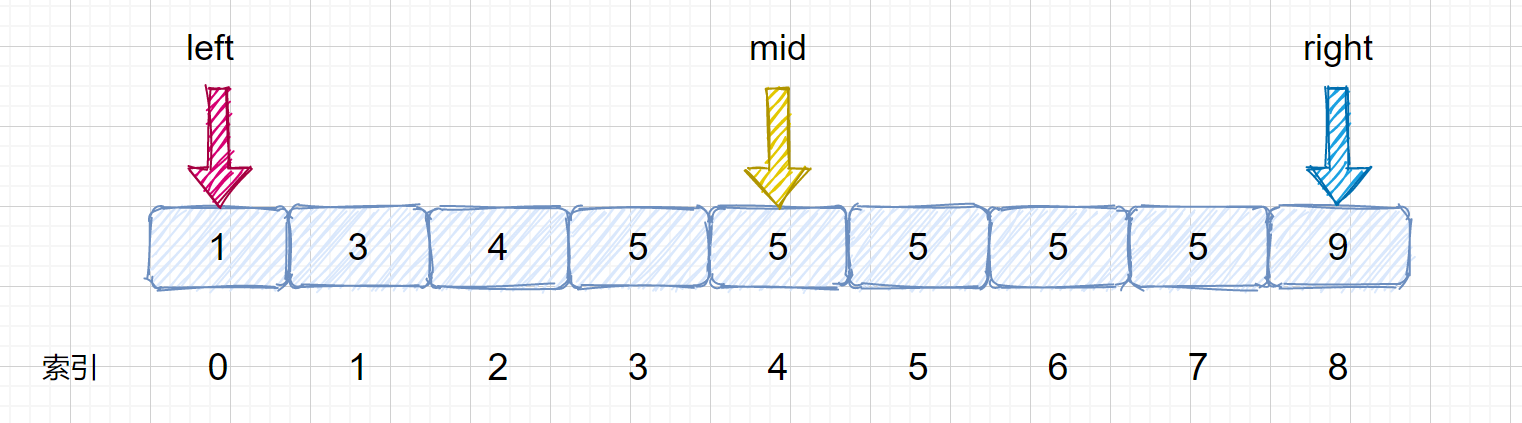![二分查找下边界](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/二分查找下边界.m9m083jempc.png)



此时 mid = 4 ，nums[mid] = 5,但是此时的 mid 指向的并不是第一个 5，所以我们需要继续查找 ，因为我们要找

的是数的下边界，所以我们需要在 mid 的值的左区间继续寻找 5 ，那我们应该怎么做呢？我们只需在 

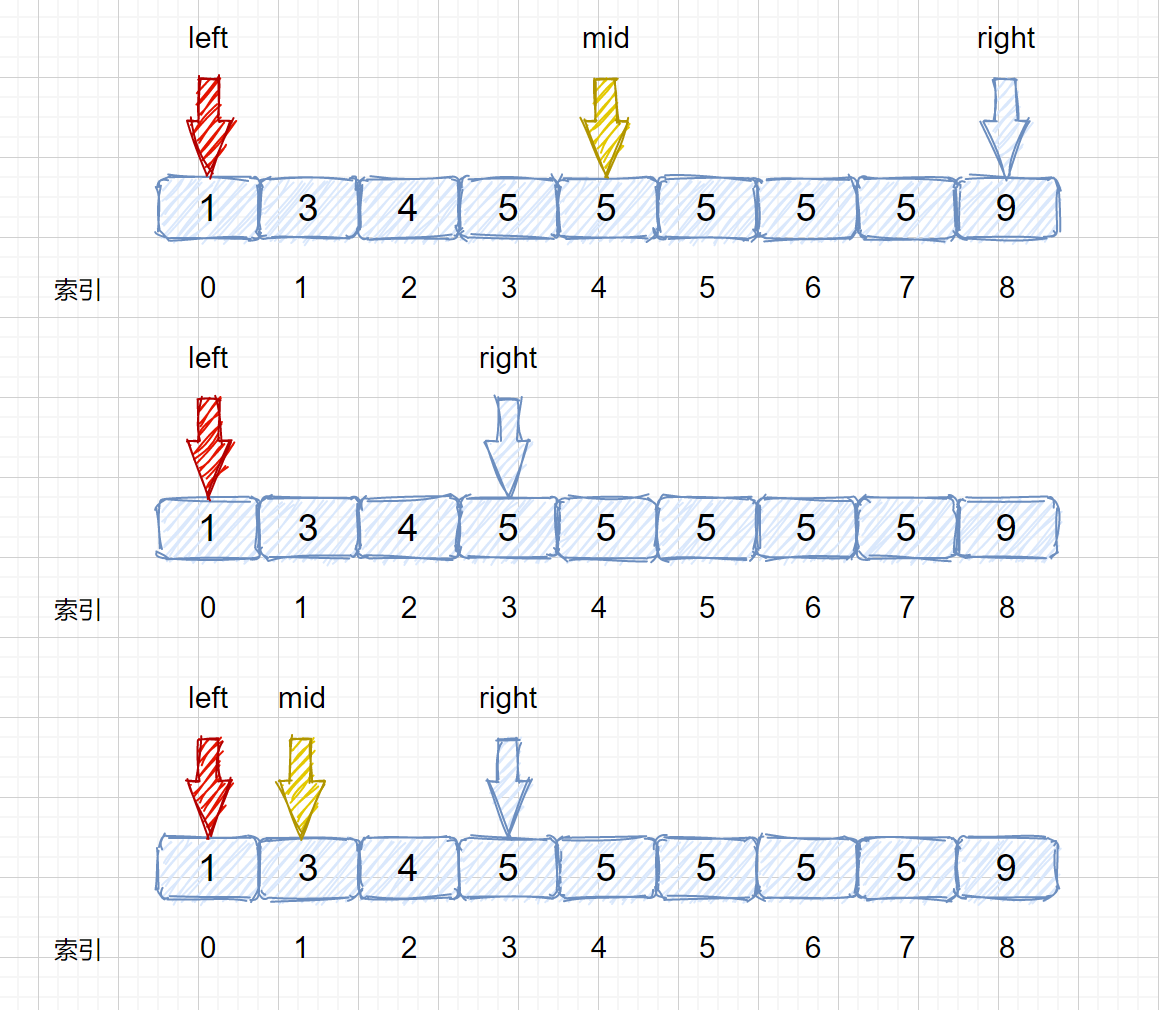
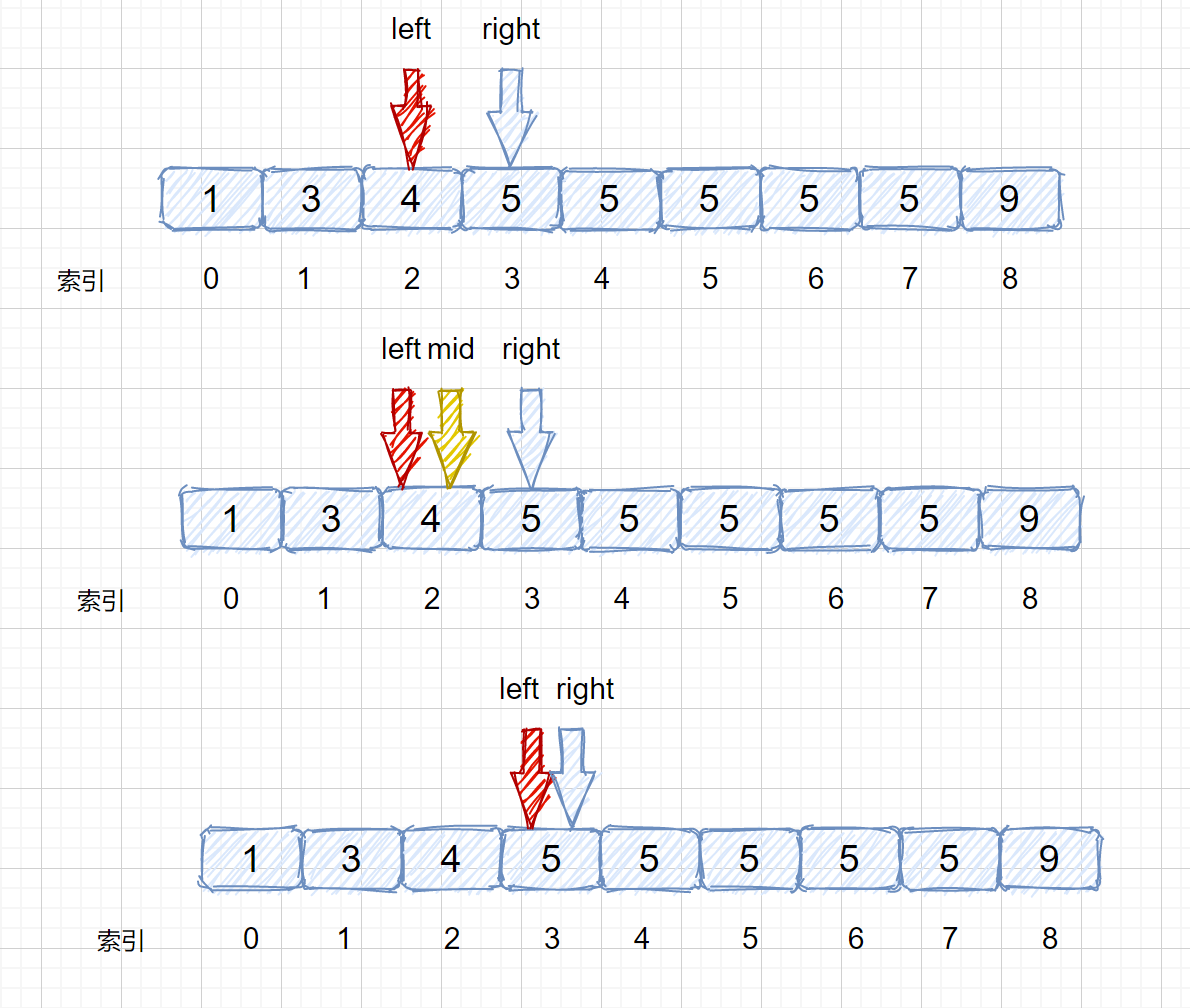
target <= nums[mid] 时，让 right = mid - 1即可，这样我们就可以继续在 mid 的左区间继续找 5 。是不是听着有点绕，我们通过下面这组图进行描述。

![左边界1](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/左边界1.5o2ihokjfg80.png)

![左边界2](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/左边界2.5wazlfm298s0.png)



其实原理很简单，就是我们将小于和等于合并在一起处理，当 target <= nums[mid] 时，我们都移动右指针，也就是 right  = mid -1，还有一个需要注意的就是，我们计算下边界时最后的返回值为 left ，当上图结束循环时，left = 3，right = 2，返回 left 刚好时我们的下边界。我们来看一下求下边界的具体执行过程。

**动图解析**

![二分查找下边界](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/二分查找下边界.u1cidx99yio.gif)

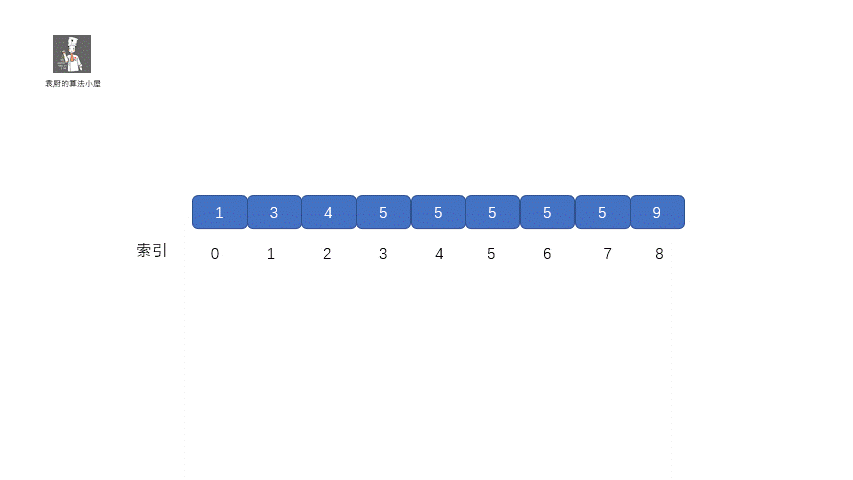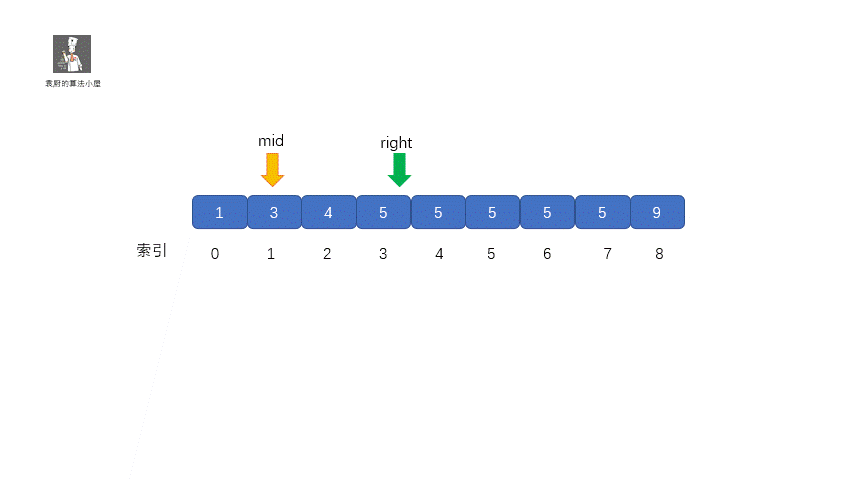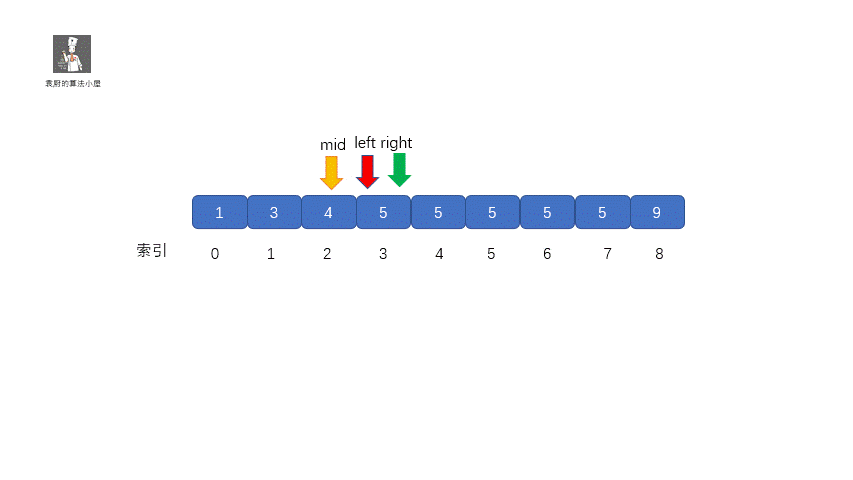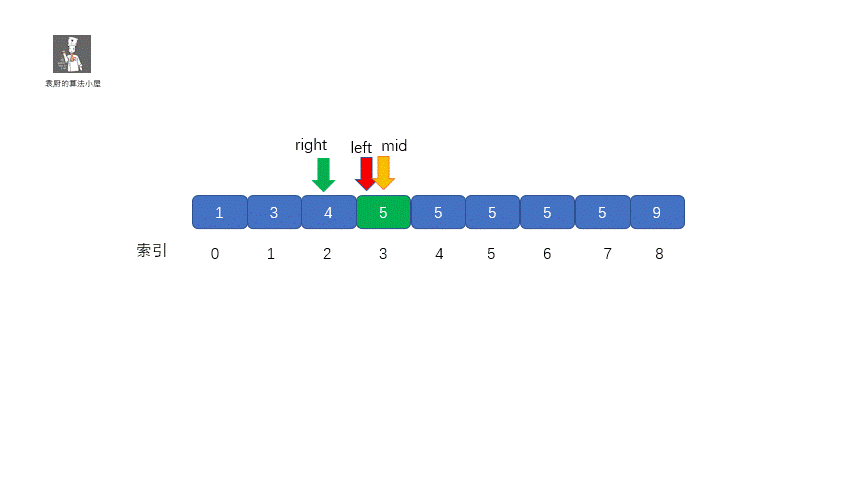
```java
int lowerBound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            //这里需要注意，计算mid
            int mid = left + ((right - left) >> 1);
            if (target <= nums[mid]) {
                //当目标值小于等于nums[mid]时，继续在左区间检索，找到第一个数
                right = mid - 1;

            }else if (target > nums[mid]) {
                //目标值大于nums[mid]时，则在右区间继续检索，找到第一个等于目标值的数
                left = mid + 1;

            }
        }
        return left;
    }
```



计算上边界时算是和计算上边界时条件相反，

计算下边界时，当  target <= nums[mid]  时，right = mid -1；target > nums[mid] 时，left = mid + 1；

计算上边界时，当  target < nums[mid] 时，right = mid -1; target >= nums[mid] 时 left = mid + 1;刚好和计算下边界时条件相反，返回right。

**计算上边界代码**

```java
int upperBound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            //求mid
            int mid = left + ((right - left) >> 1);
            //移动左指针情况
            if (target >= nums[mid]) {
                 left = mid + 1; 
            //移动右指针情况
            }else if (target < nums[mid]) {
                right = mid - 1;
            }
            
        }
        return left;
    }
```

#### **题目完整代码**

```java
class Solution {
    public int[] searchRange (int[] nums, int target) {
         int upper = upperBound(nums,target);
         int low = lowerBound(nums,target);  
         //不存在情况
         if (upper < low) {
             return new int[]{-1,-1};
         }
         return new int[]{low,upper};
    }
    //计算下边界
    int lowerBound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            //这里需要注意，计算mid
            int mid = left + ((right - left) >> 1);
            if (target <= nums[mid]) {
                //当目标值小于等于nums[mid]时，继续在左区间检索，找到第一个数
                right = mid - 1;

            }else if (target > nums[mid]) {
                //目标值大于nums[mid]时，则在右区间继续检索，找到第一个等于目标值的数
                left = mid + 1;

            }
        }
        return left;
    }
    //计算上边界
    int upperBound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {          
            int mid = left + ((right - left) >> 1);
            if (target >= nums[mid]) {
                 left = mid + 1;               
            }else if (target < nums[mid]) {
                right = mid - 1;
            }            
        }
        return right;
    }
}
```