mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-17 01:23:39 +00:00
150 lines
5.8 KiB
Markdown
150 lines
5.8 KiB
Markdown
|
|
#### leetcode 142. 环形链表 II
|
|||
|
|
|
|||
|
|
题目描述:
|
|||
|
|
|
|||
|
|
今天给大家介绍比较有特点的题目,也是一个特别经典的题目,判断链表中有没有环,并返回环的入口。
|
|||
|
|
|
|||
|
|
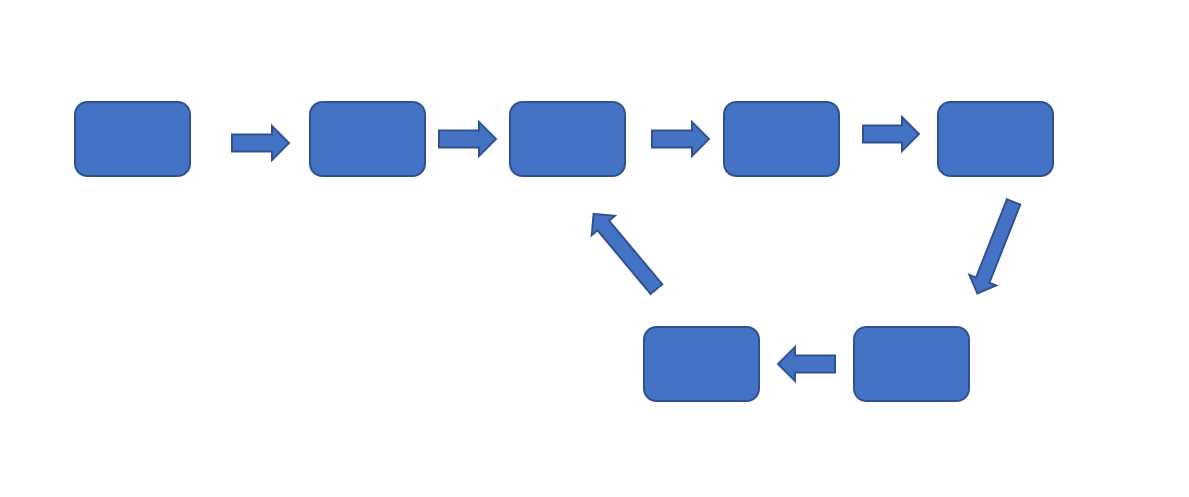
我们可以先做一下这个题目,就是如何判断链表中是否有环呢?下图则为链表存在环的情况。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
判断链表是否有环是很简单的一个问题,我们只需利用之前的快慢指针即可,大家想一下,指针只要进入环内就只能在环中循环,那么我们可以利用快慢指针,虽然慢指针的速度小于快指针但是,总会进入环中,当两个指针都处于环中时,因为移动速度不同,两个指针必会相遇。
|
|||
|
|
|
|||
|
|
我们可以这样假设,两个孩子在操场顺时针跑步,一个跑的快,一个跑的慢,跑的快的那个孩子总会追上跑的慢的孩子。
|
|||
|
|
|
|||
|
|
环形链表:
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
public class Solution {
|
|||
|
|
public boolean hasCycle(ListNode head) {
|
|||
|
|
//特殊情况,无节点或只有一个节点的情况
|
|||
|
|
if(head == null || head.next == null){
|
|||
|
|
return false;
|
|||
|
|
}
|
|||
|
|
//设置快慢指针
|
|||
|
|
ListNode pro = head.next;
|
|||
|
|
ListNode last = head;
|
|||
|
|
//循环条件
|
|||
|
|
while( pro != null && pro.next!=null){
|
|||
|
|
pro=pro.next.next;
|
|||
|
|
last=last.next;
|
|||
|
|
//两指针相遇
|
|||
|
|
if(pro == last){
|
|||
|
|
return true;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
//循环结束,指针没有相遇,说明没有环。相当于快指针遍历了一遍链表
|
|||
|
|
return false;
|
|||
|
|
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
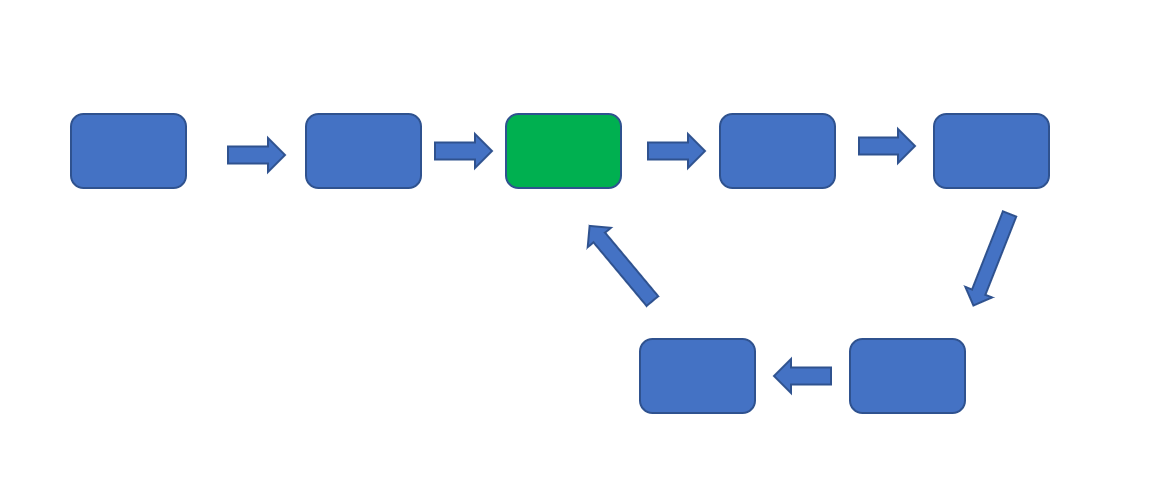
判断链表是不是含有环很简单,但是我们想找到环的入口可能就没有那么容易了。(入口则为下图绿色节点)
|
|||
|
|
|
|||
|
|
然后我们返回的则为绿色节点的索引,则返回2。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
### HashSet
|
|||
|
|
|
|||
|
|
我们可以利用HashSet来做,之前的文章说过HashSet是一个不允许有重复元素的集合。所以我们通过HashSet来保存链表节点,对链表进行遍历,如果链表不存在环则每个节点都会被存入环中,但是当链表中存在环时,则会发重复存储链表节点的情况,所以当我们发现HashSet中含有某节点时说明该节点为环的入口,返回即可。
|
|||
|
|
|
|||
|
|
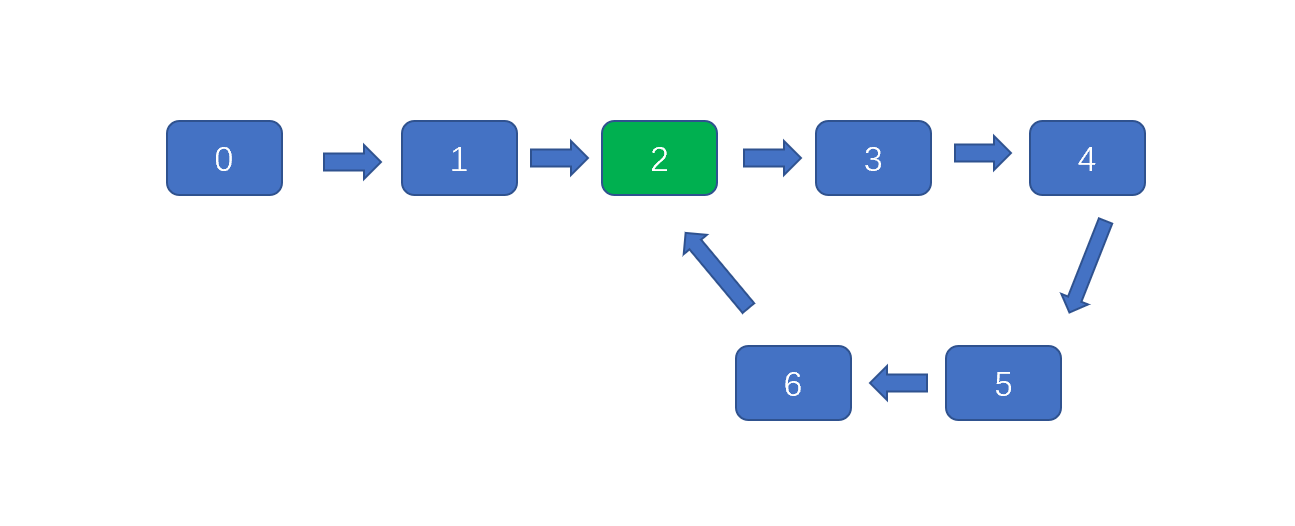
下图中,存储顺序为 0,1,2,3,4,5,6,**2 **因为2已经存在,则返回。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
public class Solution {
|
|||
|
|
public ListNode detectCycle(ListNode head) {
|
|||
|
|
|
|||
|
|
if (head == null) {
|
|||
|
|
return head;
|
|||
|
|
}
|
|||
|
|
if (head.next == null) {
|
|||
|
|
return head.next;
|
|||
|
|
}
|
|||
|
|
//创建新的HashSet,用于保存节点
|
|||
|
|
HashSet<ListNode> hash = new HashSet<ListNode>();
|
|||
|
|
//遍历链表
|
|||
|
|
while (head != null) {
|
|||
|
|
//判断哈希表中是否含有某节点,没有则保存,含有则返回该节点
|
|||
|
|
if (hash.contains(head)) {
|
|||
|
|
return head;
|
|||
|
|
}
|
|||
|
|
//不含有,则进行保存,并移动指针
|
|||
|
|
hash.add(head);
|
|||
|
|
head = head.next;
|
|||
|
|
}
|
|||
|
|
return head;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
### 快慢指针
|
|||
|
|
|
|||
|
|
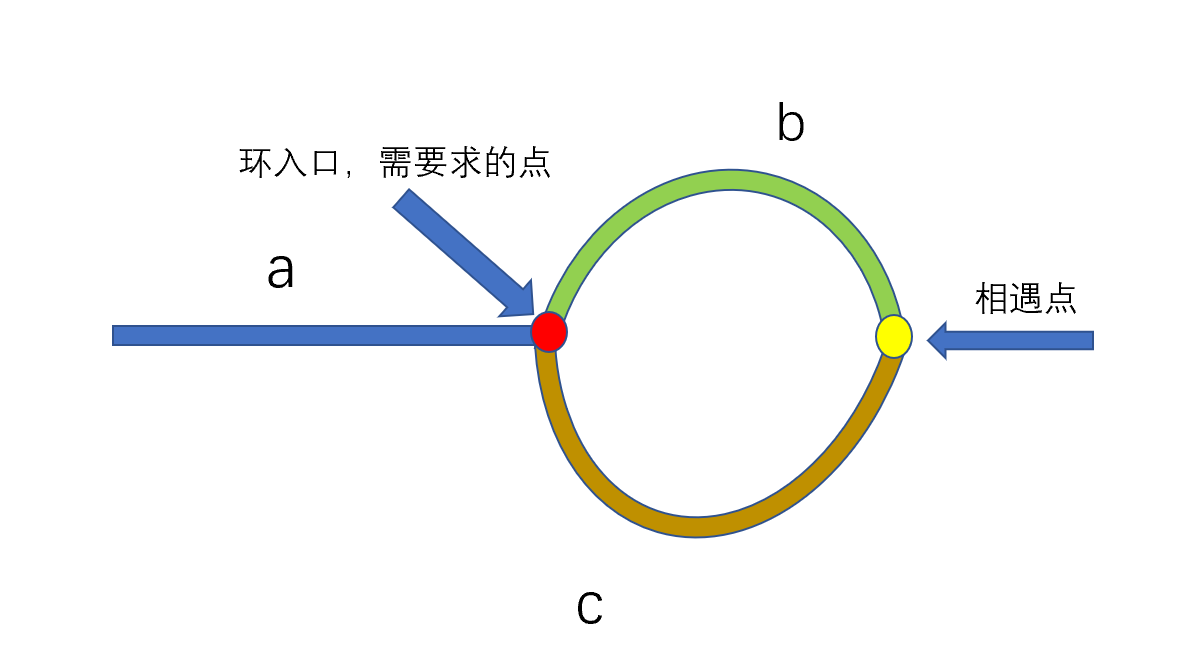
这个方法是比较巧妙的方法,但是不容易想到,也不太容易理解,利用快慢指针判断是否有环很容易,但是判断环的入口就没有那么容易,之前说过快慢指针肯定会在环内相遇,见下图。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
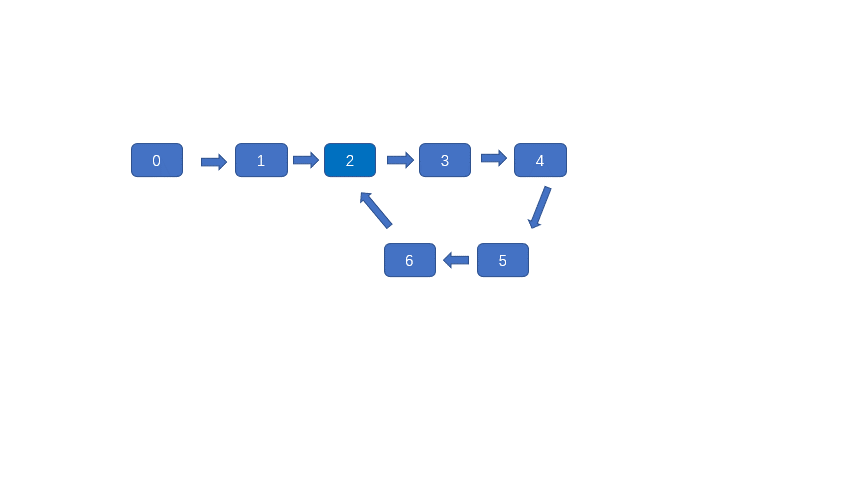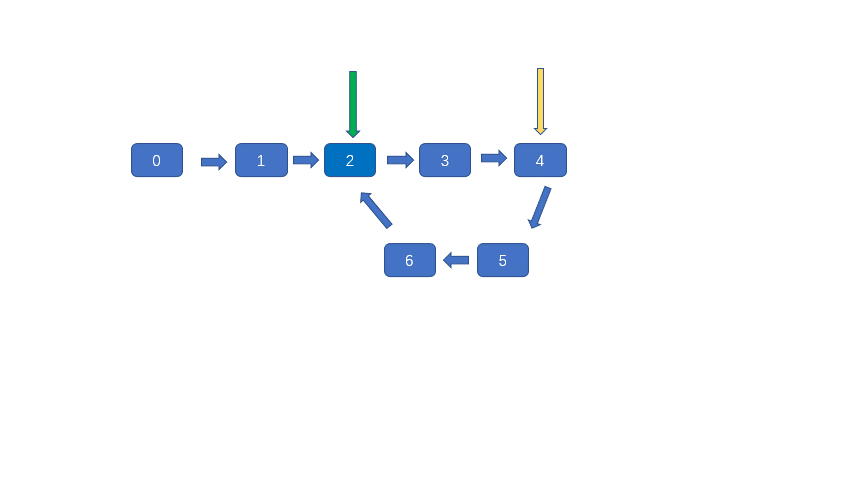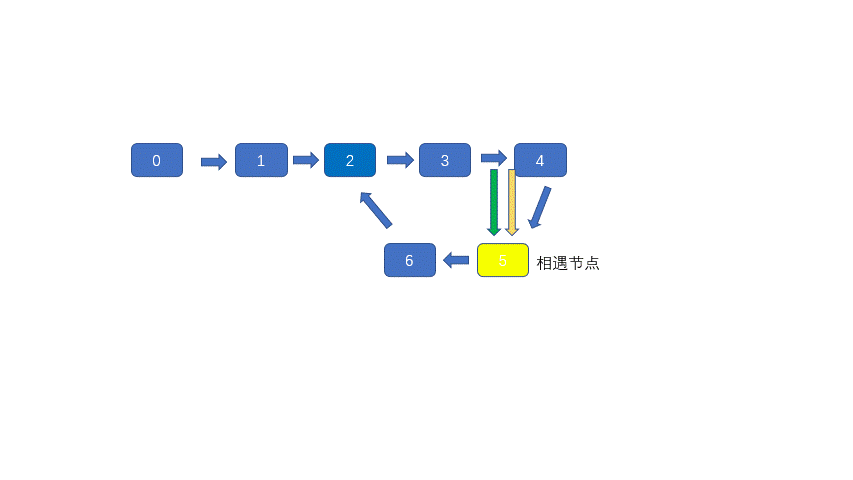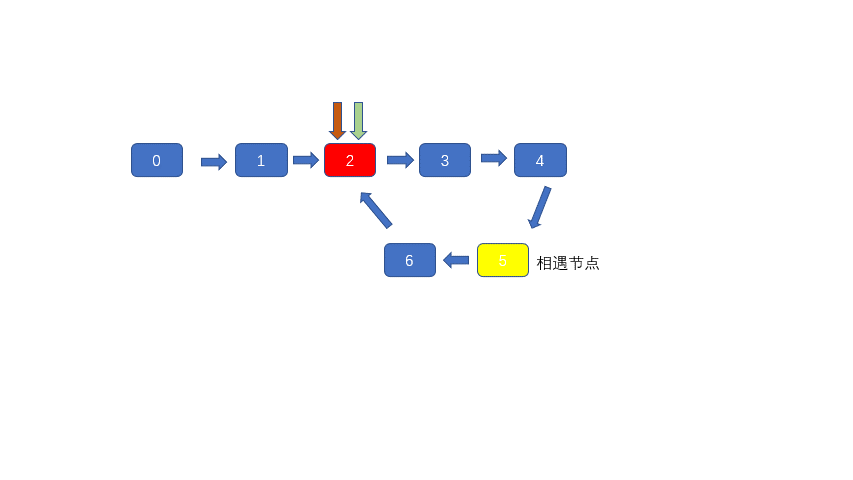
上图黄色节点为快慢指针相遇的节点,此时
|
|||
|
|
|
|||
|
|
快指针走的距离:**a+(b+c)n+b**
|
|||
|
|
|
|||
|
|
很容易理解b+c为环的长度,a为直线距离,b为绕了n圈之后又走了一段距离才相遇,所以相遇时走的总路程为a+(b+c)n+b,合并同类项得a+(n+1)b+nc。
|
|||
|
|
|
|||
|
|
慢指针走的距离:**a+(b+c)m+b**,m代表圈数。
|
|||
|
|
|
|||
|
|
然后我们设快指针得速度是慢指针的2倍,含义为相同时间内,快指针走过的距离是慢指针的2倍。
|
|||
|
|
|
|||
|
|
**a+(n+1)b+nc=2[a+(m+1)b+mc]**整理得**a+b=(n-2m)(b+c),**那么我们可以从这个等式上面发现什么呢?**b+c**
|
|||
|
|
|
|||
|
|
为一圈的长度。也就是说a+b等于n-2m个环的长度。为了便于理解我们看一种特殊情况,当n-2m等于1,那么a+b=b+c整理得,a=c此时我们只需重新释放两个指针,一个从head释放,一个从相遇点释放,速度相同,因为a=c所以他俩必会在环入口处相遇,则求得入口节点索引。
|
|||
|
|
|
|||
|
|
算法流程:
|
|||
|
|
|
|||
|
|
1.设置快慢指针,快指针速度为慢指针的2倍
|
|||
|
|
|
|||
|
|
2.找出相遇点
|
|||
|
|
|
|||
|
|
3.在head处和相遇点同时释放相同速度且速度为1的指针,两指针必会在环入口处相遇
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
```java
|
|||
|
|
public class Solution {
|
|||
|
|
public ListNode detectCycle(ListNode head) {
|
|||
|
|
//快慢指针
|
|||
|
|
ListNode fast = head;
|
|||
|
|
ListNode low = head;
|
|||
|
|
//设置循环条件
|
|||
|
|
while (fast != null && fast.next != null) {
|
|||
|
|
fast = fast.next.next;
|
|||
|
|
low = low.next;
|
|||
|
|
//相遇
|
|||
|
|
if (fast == low) {
|
|||
|
|
//设置一个新的指针,从头节点出发,慢指针速度为1,所以可以使用慢指针从相遇点出发
|
|||
|
|
ListNode newnode = head;
|
|||
|
|
while (newnode != low) {
|
|||
|
|
low = low.next;
|
|||
|
|
newnode = newnode.next;
|
|||
|
|
}
|
|||
|
|
//在环入口相遇
|
|||
|
|
return low;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
return null;
|
|||
|
|
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|