mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-12-26 20:36:18 +00:00
chefyuan
This commit is contained in:
parent
1fc9cabcf2
commit
4496ab0198
@ -52,6 +52,7 @@
|
|||||||
- [【绘图描述】leetcode 66 加一](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode66%E5%8A%A0%E4%B8%80.md)
|
- [【绘图描述】leetcode 66 加一](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode66%E5%8A%A0%E4%B8%80.md)
|
||||||
- [【动画模拟】leetcode 75 颜色分类](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode75%E9%A2%9C%E8%89%B2%E5%88%86%E7%B1%BB.md)
|
- [【动画模拟】leetcode 75 颜色分类](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode75%E9%A2%9C%E8%89%B2%E5%88%86%E7%B1%BB.md)
|
||||||
- [【动画模拟】leetcode 54 螺旋矩阵](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode54%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5.md)
|
- [【动画模拟】leetcode 54 螺旋矩阵](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode54%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5.md)
|
||||||
|
- [【动画模拟】leetcode 59 螺旋矩阵2](https://github.com/chefyuan/algorithm-base/blob/main/gif-algorithm/%E6%95%B0%E7%BB%84%E7%AF%87/leetcode59%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B52.md)
|
||||||
|
|
||||||
### 链表篇
|
### 链表篇
|
||||||
|
|
||||||
|
|||||||
1
animation-simulation/数据结构和算法
Submodule
1
animation-simulation/数据结构和算法
Submodule
@ -0,0 +1 @@
|
|||||||
|
Subproject commit e42a9602ab07502123c1faa023ce759693702a86
|
||||||
@ -1,128 +0,0 @@
|
|||||||
> 为保证代码严谨性,文中所有代码均在 leetcode 刷题网站 AC ,大家可以放心食用。
|
|
||||||
|
|
||||||
皇上生辰之际,举国同庆,袁记菜馆作为天下第一饭店,所以被选为这次庆典的菜品供应方,这次庆典对于袁记菜馆是一项前所未有的挑战,毕竟是第一次给皇上庆祝生辰,稍有不慎就是掉脑袋的大罪,整个袁记菜馆内都在紧张的布置着。此时突然有一个店小二慌慌张张跑到袁厨面前汇报,到底发生了什么事,让店小二如此慌张呢?
|
|
||||||
|
|
||||||
袁记菜馆内
|
|
||||||
|
|
||||||
店小二:不好了不好了,掌柜的,出大事了。
|
|
||||||
|
|
||||||
袁厨:发生什么事了,慢慢说,如此慌张,成何体统。(开店开久了,架子出来了哈)
|
|
||||||
|
|
||||||
店小二:皇上按照咱们菜单点了 666 道菜,但是咱们做西湖醋鱼的师傅请假回家结婚了,不知道皇上有没有点这道菜,如果点了这道菜,咱们做不出来,那咱们店可就完了啊。
|
|
||||||
|
|
||||||
(袁厨听了之后,吓得一屁股坐地上了,缓了半天说道)
|
|
||||||
|
|
||||||
袁厨:别说那么多了,快给我找找皇上点的菜里面,有没有这道菜!
|
|
||||||
|
|
||||||
找了很久,并且核对了很多遍,最后确认皇上没有点这道菜。菜馆内的人都松了一口气
|
|
||||||
|
|
||||||
通过上面的一个例子,让我们简单了解了字符串匹配。
|
|
||||||
|
|
||||||
字符串匹配:设 S 和 T 是给定的两个串,在主串 S 中找到模式串 T 的过程称为字符串匹配,如果在主串 S 中找到 模式串 T ,则称匹配成功,函数返回 T 在 S 中首次出现的位置,否则匹配不成功,返回 -1。
|
|
||||||
|
|
||||||
例:
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
在上图中,我们试图找到模式 T = baab,在主串 S = abcabaabcabac 中第一次出现的位置,即为红色阴影部分, T 第一次在 S 中出现的位置下标为 4 ( 字符串的首位下标是 0 ),所以返回 4。如果模式串 T 没有在主串 S 中出现,则返回 -1。
|
|
||||||
|
|
||||||
解决上面问题的算法我们称之为字符串匹配算法,今天我们来介绍三种字符串匹配算法,大家记得打卡呀,说不准面试的时候就问到啦。
|
|
||||||
|
|
||||||
## BF算法(Brute Force)
|
|
||||||
|
|
||||||
这个算法很容易理解,就是我们将模式串和主串进行比较,一致时则继续比较下一字符,直到比较完整个模式串。不一致时则将模式串后移一位,重新从模式串的首位开始对比,重复刚才的步骤下面我们看下这个方法的动图解析,看完肯定一下就能搞懂啦。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
通过上面的代码是不是一下就将这个算法搞懂啦,下面我们用这个算法来解决下面这个经典题目吧。
|
|
||||||
|
|
||||||
### leetcdoe 28. 实现 strStr()
|
|
||||||
|
|
||||||
#### 题目描述
|
|
||||||
|
|
||||||
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
|
|
||||||
|
|
||||||
示例 1:
|
|
||||||
|
|
||||||
> 输入: haystack = "hello", needle = "ll"
|
|
||||||
> 输出: 2
|
|
||||||
|
|
||||||
示例 2:
|
|
||||||
|
|
||||||
> 输入: haystack = "aaaaa", needle = "bba"
|
|
||||||
> 输出: -1
|
|
||||||
|
|
||||||
#### 题目解析
|
|
||||||
|
|
||||||
其实这个题目很容易理解,但是我们需要注意的是一下几点,比如我们的模式串为 0 时,应该返回什么,我们的模式串长度大于主串长度时,应该返回什么,也是我们需要注意的地方。下面我们来看一下题目代码吧。
|
|
||||||
|
|
||||||
#### 题目代码
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
int haylen = haystack.length();
|
|
||||||
int needlen = needle.length();
|
|
||||||
//特殊情况
|
|
||||||
if (haylen < needlen) {
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
if (needlen == 0) {
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
//主串
|
|
||||||
for (int i = 0; i < haylen - needlen + 1; ++i) {
|
|
||||||
int j;
|
|
||||||
//模式串
|
|
||||||
for (j = 0; j < needlen; j++) {
|
|
||||||
//不符合的情况,直接跳出,主串指针后移一位
|
|
||||||
if (haystack.charAt(i+j) != needle.charAt(j)) {
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//匹配成功
|
|
||||||
if (j == needlen) {
|
|
||||||
return i;
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们看一下BF算法的另一种算法(显示回退),其实原理一样,就是对代码进行了一下修改,只要是看完咱们的动图,这个也能够一下就能看懂,大家可以结合下面代码中的注释和动图进行理解。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
//i代表主串指针,j模式串
|
|
||||||
int i,j;
|
|
||||||
//主串长度和模式串长度
|
|
||||||
int halen = haystack.length();
|
|
||||||
int nelen = needle.length();
|
|
||||||
//循环条件,这里只有 i 增长
|
|
||||||
for (i = 0 , j = 0; i < halen && j < nelen; ++i) {
|
|
||||||
//相同时,则移动 j 指针
|
|
||||||
if (haystack.charAt(i) == needle.charAt(j)) {
|
|
||||||
++j;
|
|
||||||
} else {
|
|
||||||
//不匹配时,将 j 重新指向模式串的头部,将 i 本次匹配的开始位置的下一字符
|
|
||||||
i -= j;
|
|
||||||
j = 0;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//查询成功时返回索引,查询失败时返回 -1;
|
|
||||||
int renum = j == nelen ? i - nelen : -1;
|
|
||||||
return renum;
|
|
||||||
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
@ -1,214 +0,0 @@
|
|||||||
## BM算法(Boyer-Moore)
|
|
||||||
|
|
||||||
我们刚才说过了 BF 算法,但是 BF 算法是有缺陷的,比如我们下面这种情况
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如上图所示,如果我们利用 BF 算法,遇到不匹配字符时,每次右移一位模式串,再重新从头进行匹配,我们观察一下,我们的模式串 abcdex 中每个字符都不一样,但是我们第一次进行字符串匹配时,abcde 都匹配成功,到 x 时失败,又因为模式串每位都不相同,所以我们不需要再每次右移一位,再重新比较,我们可以直接跳过某些步骤。如下图
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们可以跳过其中某些步骤,直接到下面这个步骤。那我们是依据什么原则呢?
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
### 坏字符规则
|
|
||||||
|
|
||||||
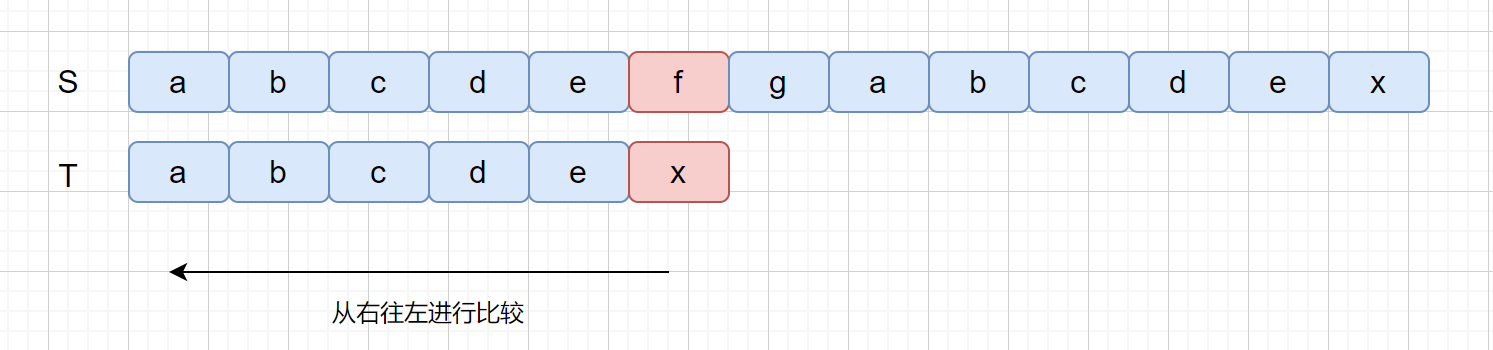
我们之前的 BF 算法是从前往后进行比较 ,BM 算法是从后往前进行比较,我们来看一下具体过程,我们还是利用上面的例子。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
BM 算法是从后往前进行比较,此时我们发现比较的第一个字符就不匹配,我们将**主串**这个字符称之为**坏字符**,也就是 f ,我们发现坏字符之后,模式串 T 中查找是否含有该字符(f),我们发现并不存在 f,此时我们只需将模式串右移到坏字符的后面一位即可。如下图
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
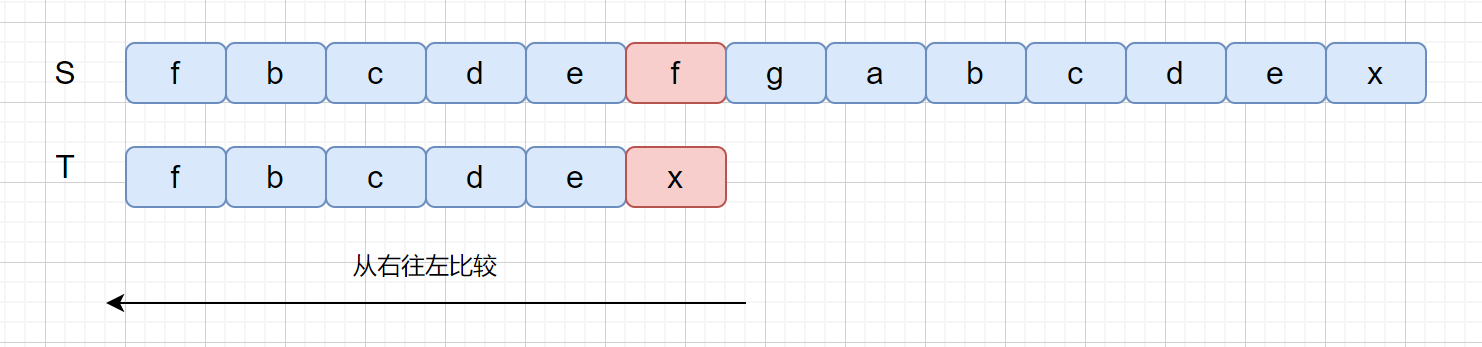
那我们在模式串中找到坏字符该怎么办呢?
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时我们的坏字符为 f ,我们在模式串中,查找发现含有坏字符 f,我们则需要移动模式串 T ,将模式串中的 f 和坏字符对齐。见下图。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
然后我们继续从右往左进行比较,发现 d 为坏字符,则需要将模式串中的 d 和坏字符对齐。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
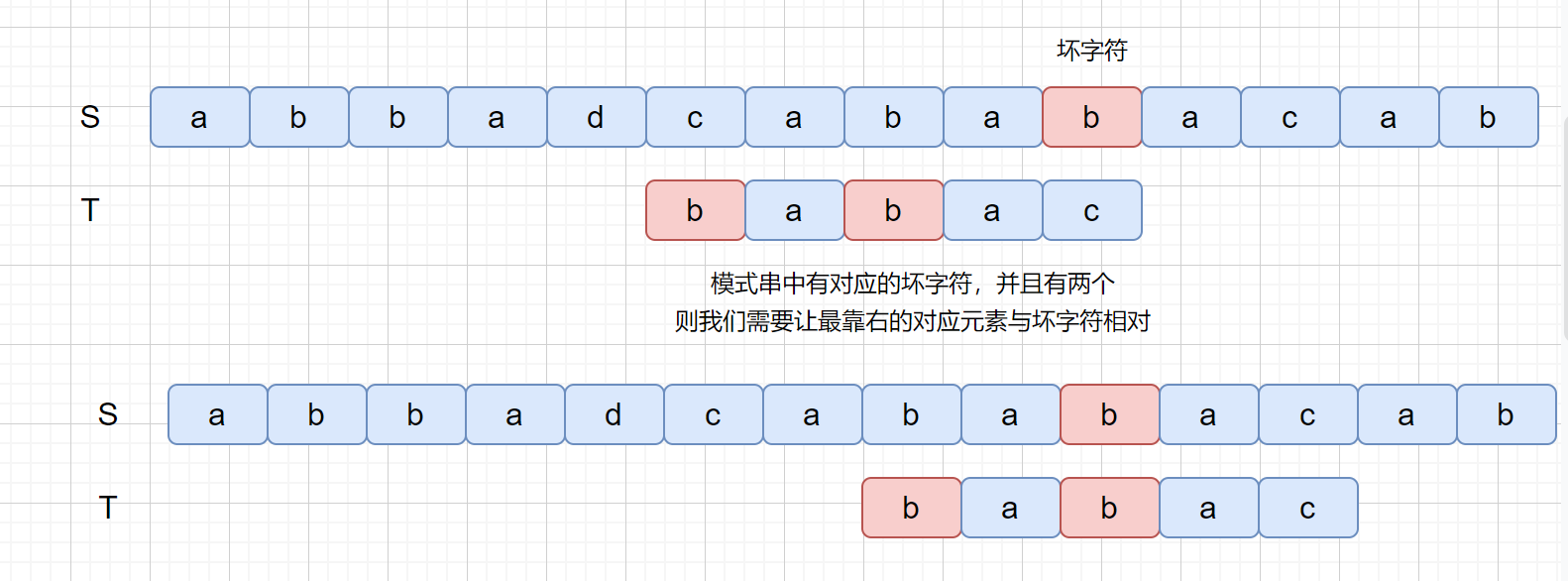
那么我们在来思考一下这种情况,那就是模式串中含有多个坏字符怎么办呢?
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
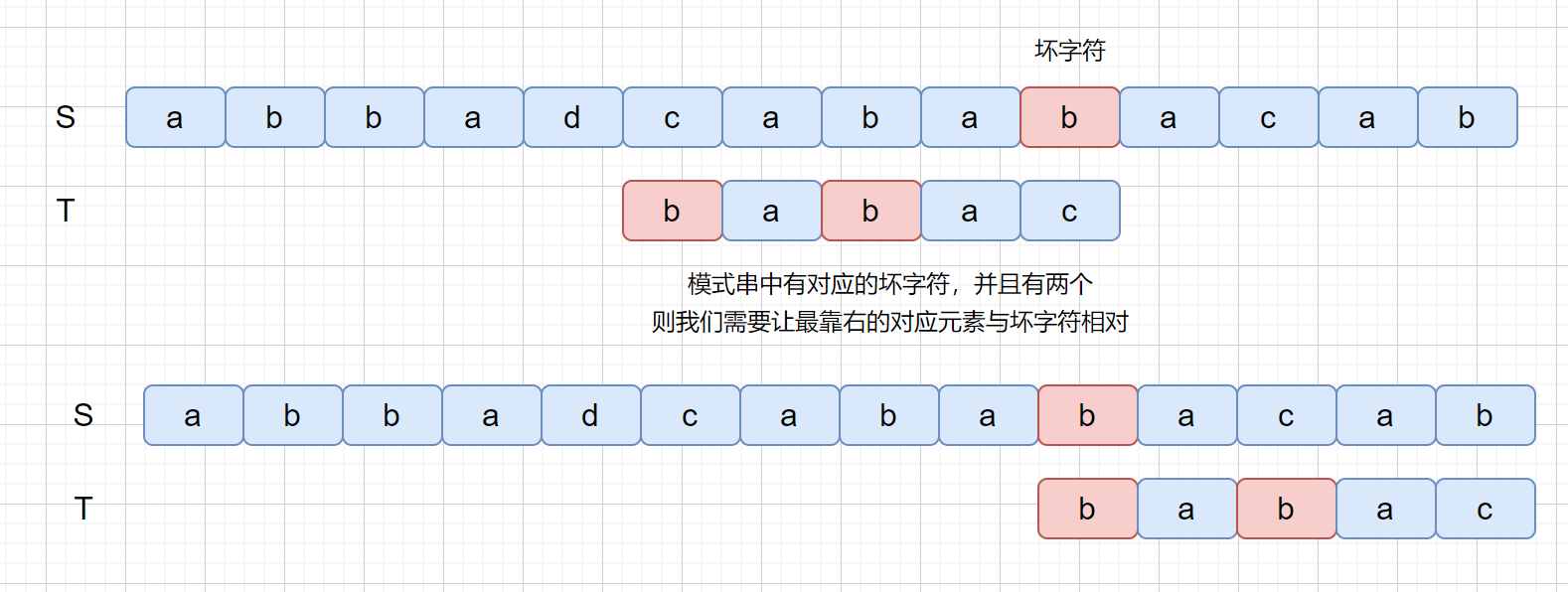
那么我们为什么要让**最靠右的对应元素与坏字符匹配**呢?如果上面的例子我们没有按照这条规则看下会产生什么问题。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如果没有按照我们上述规则,则会**漏掉我们的真正匹配**。我们的主串中是**含有 babac** 的,但是却**没有匹配成功**,所以应该遵守**最靠右的对应字符与坏字符相对**的规则。
|
|
||||||
|
|
||||||
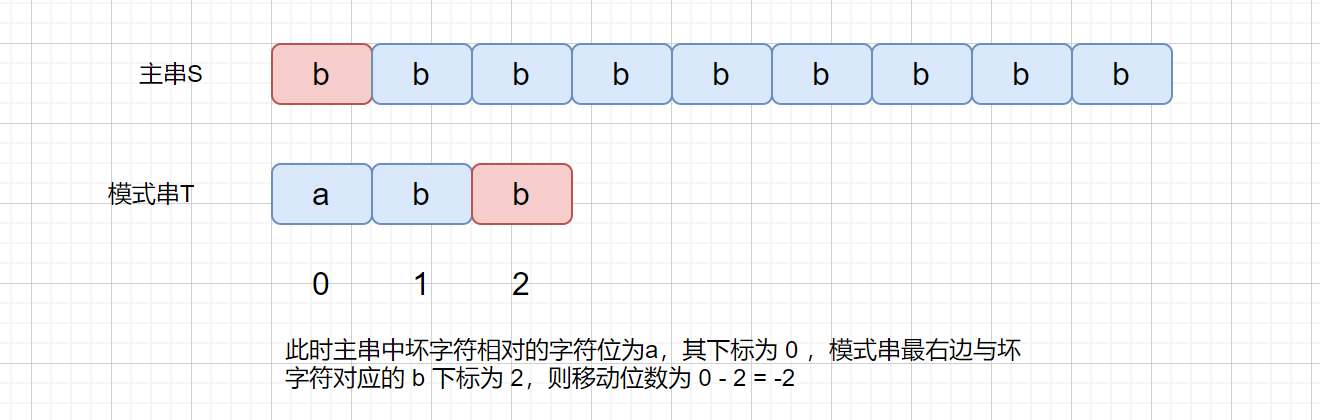
我们上面一共介绍了三种移动情况,分别是下方的模式串中没有发现与坏字符对应的字符,发现一个对应字符,发现两个。这三种情况我们分别移动不同的位数,那我们是根据依据什么来决定移动位数的呢?下面我们给图中的字符加上下标。见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
下面我们来考虑一下这种情况。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时这种情况肯定是不行的,不往右移动,甚至还有可能左移,那么我们有没有什么办法解决这个问题呢?继续往下看吧。
|
|
||||||
|
|
||||||
### 好后缀规则
|
|
||||||
|
|
||||||
好后缀其实也很容易理解,我们之前说过 BM 算法是从右往左进行比较,下面我们来看下面这个例子。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
这里如果我们按照坏字符进行移动是不合理的,这时我们可以使用好后缀规则,那么什么是好后缀呢?
|
|
||||||
|
|
||||||
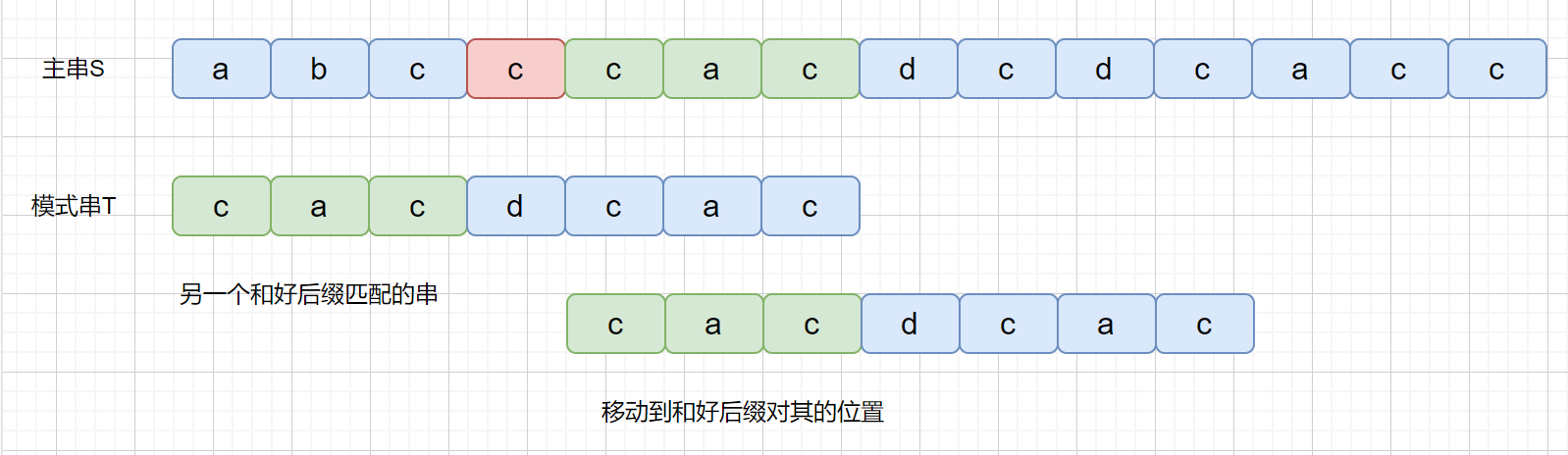
BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已经匹配成功,在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀,此时我们拿它在模式串中查找,如果找到了另一个和好后缀相匹配的串,那我们就将另一个和**好后缀相匹配**的串 ,滑到和好后缀对齐的位置。
|
|
||||||
|
|
||||||
是不是感觉有点拗口,没关系,我们看下图,红色代表坏字符,绿色代表好后缀
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
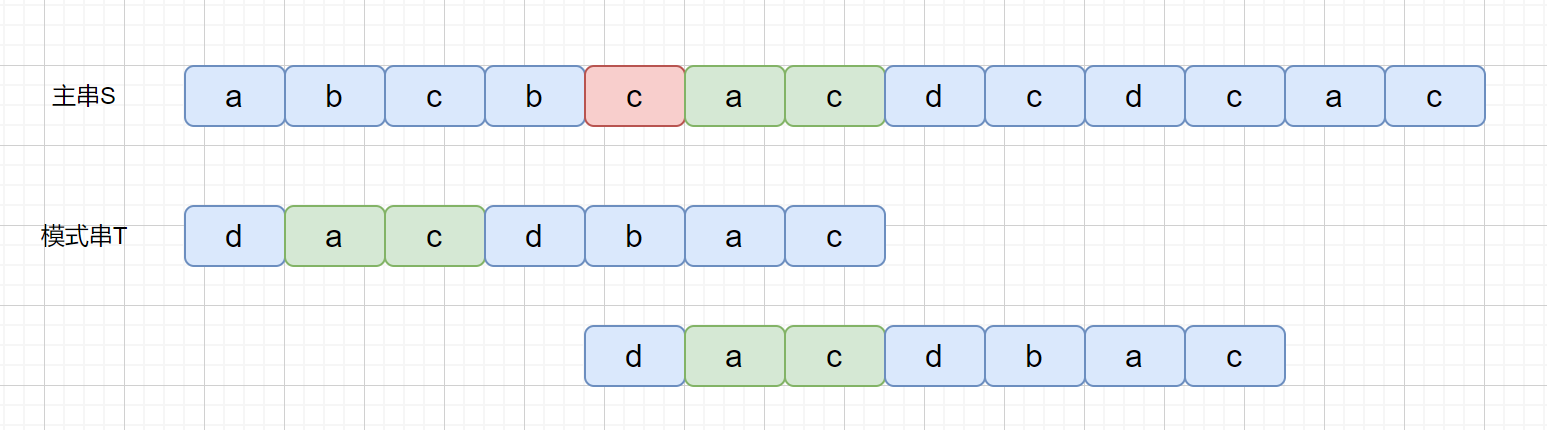
上面那种情况搞懂了,但是我们思考一下下面这种情况
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
上面我们说到了,如果在模式串的**头部**没有发现好后缀,发现好后缀的子串也可以。但是为什么要强调这个头部呢?
|
|
||||||
|
|
||||||
我们下面来看一下这种情况
|
|
||||||
|
|
||||||
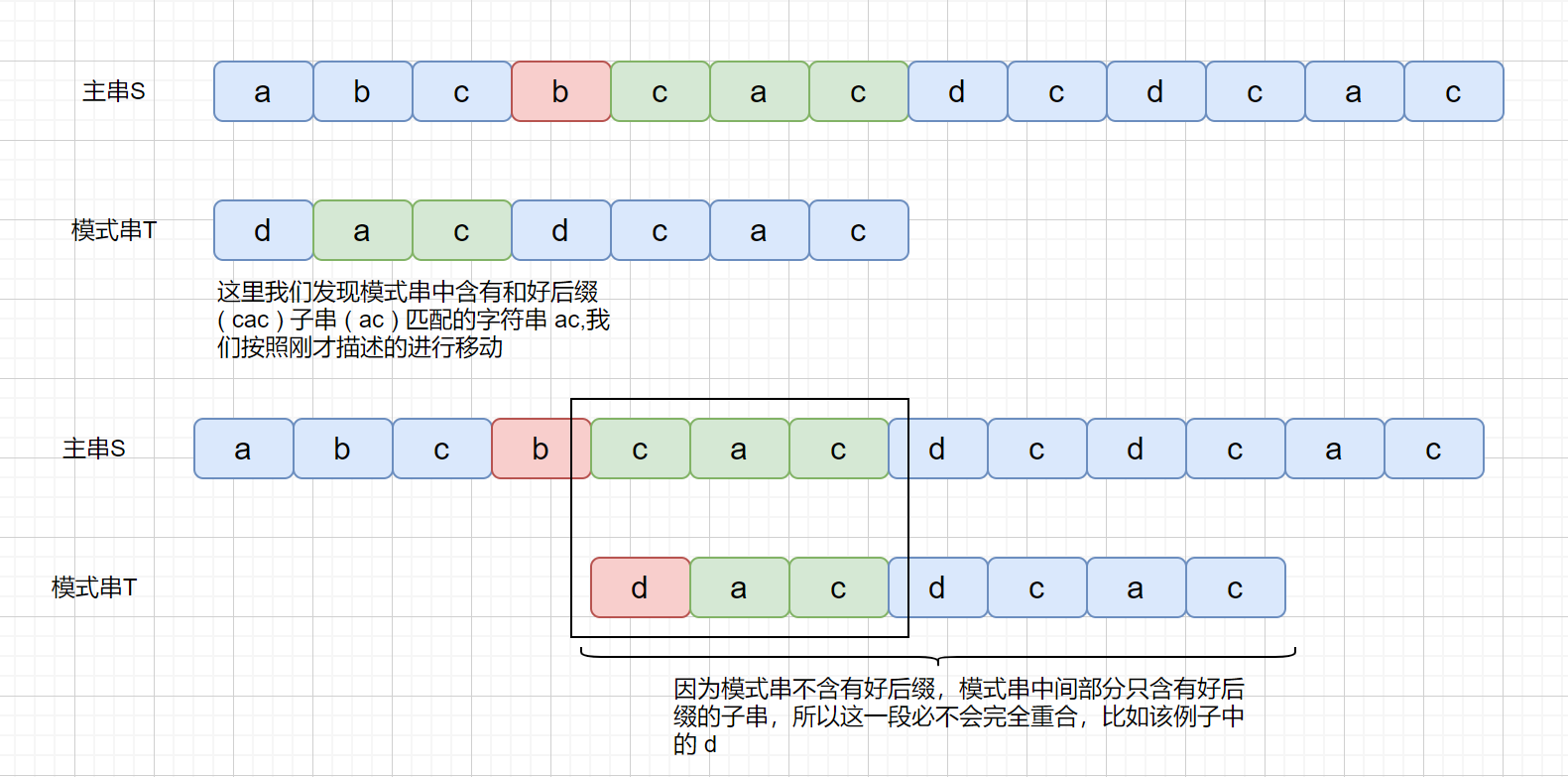
|
|
||||||
|
|
||||||
但是当我们在头部发现好后缀的子串时,是什么情况呢?
|
|
||||||
|
|
||||||
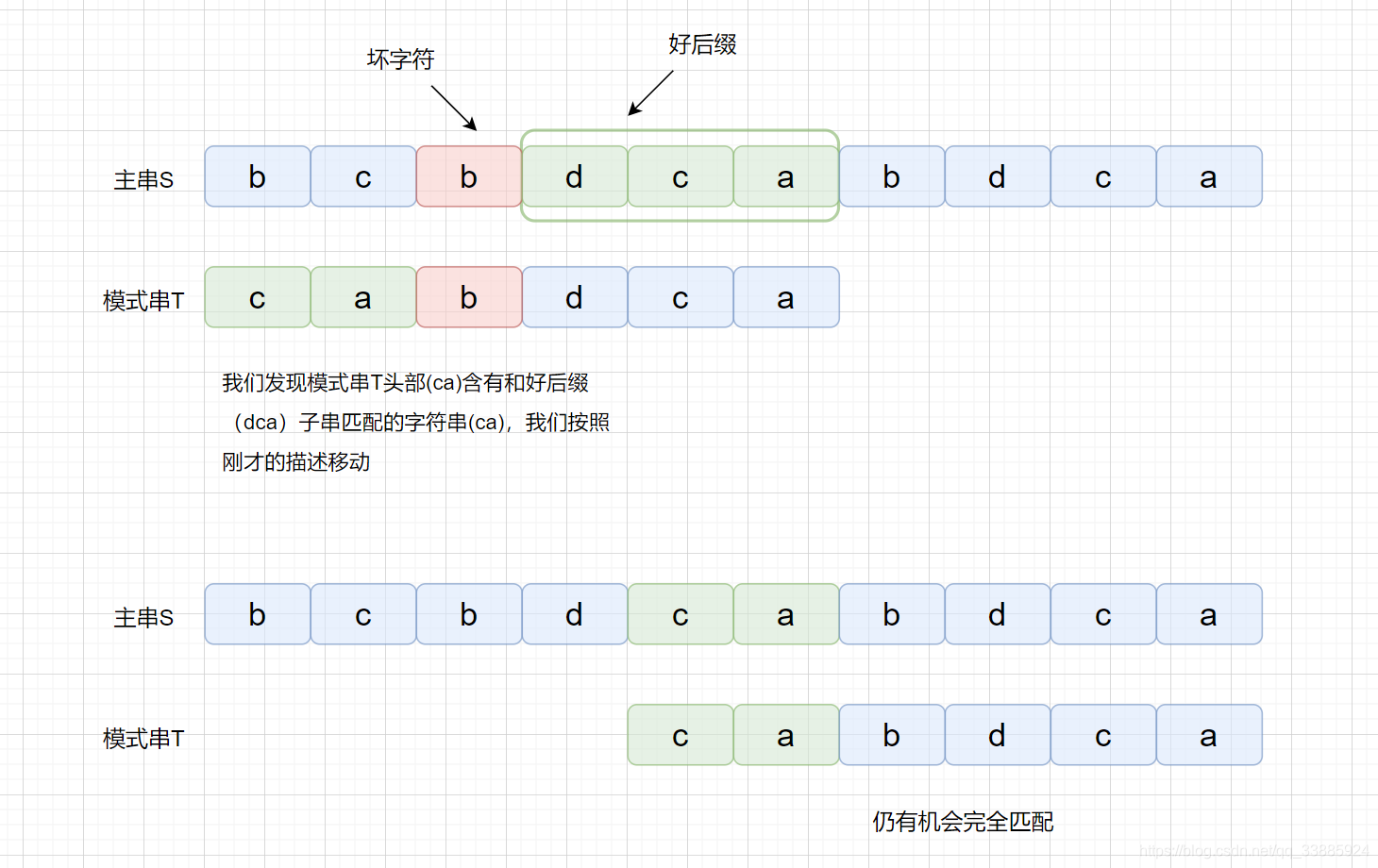
|
|
||||||
|
|
||||||
下面我们通过动图来看一下某一例子的具体的执行过程
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
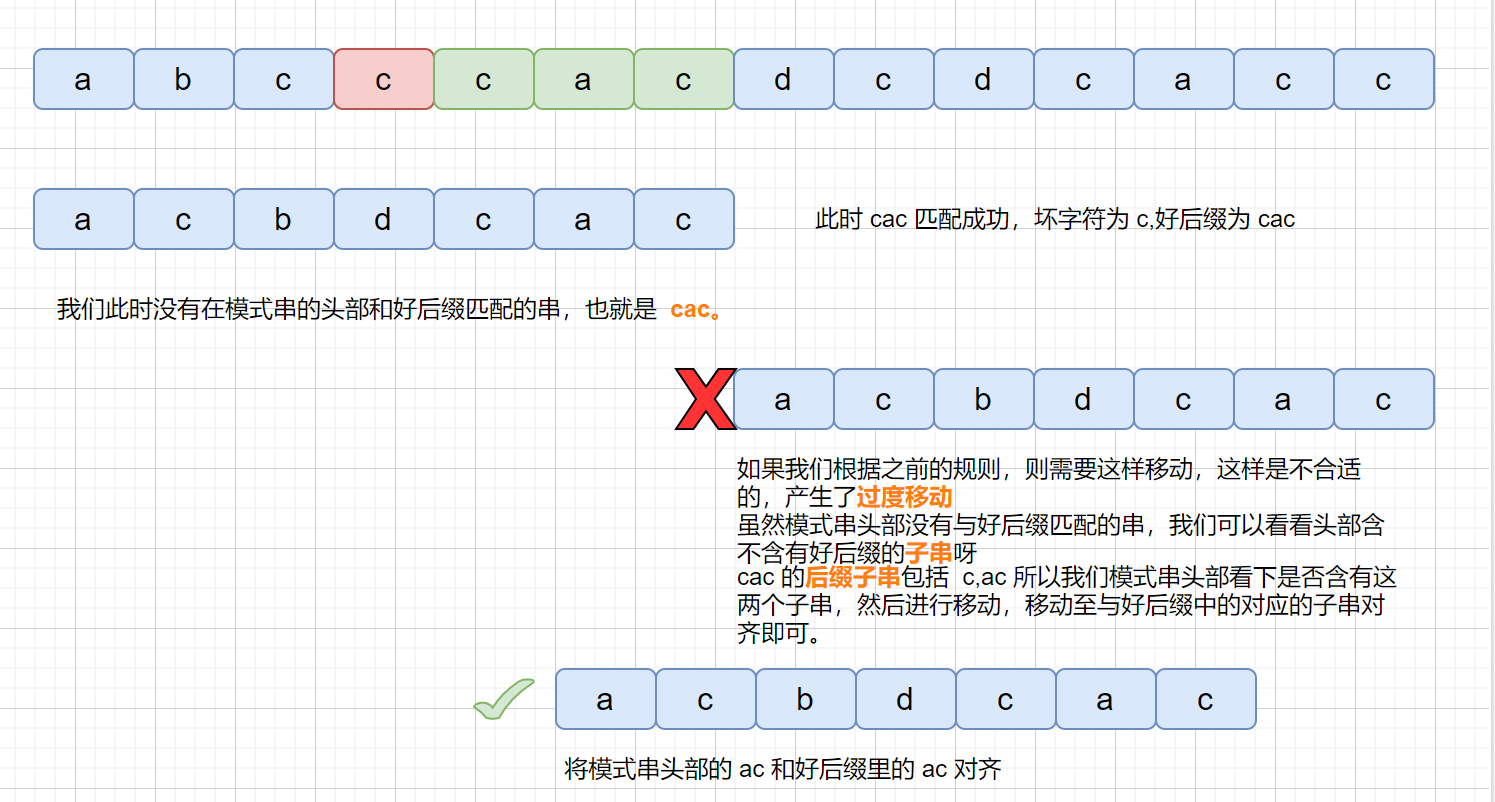
说到这里,坏字符和好后缀规则就算说完了,坏字符很容易理解,我们对好后缀总结一下
|
|
||||||
|
|
||||||
1.如果模式串**含有好后缀**,无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次,则以**最右侧的好后缀**为基准。
|
|
||||||
|
|
||||||
2.如果模式串**头部含有**好后缀子串则可以按照规则进行移动,中间部分含有好后缀子串则不可以。
|
|
||||||
|
|
||||||
3.如果在模式串尾部就出现不匹配的情况,即不存在好后缀时,则根据坏字符进行移动,这里有的文章没有提到,是个需要特别注意的地方,我是在这个论文里找到答案的,感兴趣的同学可以看下。
|
|
||||||
|
|
||||||
> Boyer R S,Moore J S. A fast string searching algorithm[J]. Communications of the ACM,1977,10: 762-772.
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
之前我们刚开始说坏字符的时候,是不是有可能会出现负值的情况,即往左移动的情况,所以我们为了解决这个问题,我们可以分别计算好后缀和坏字符往后滑动的位数**(好后缀不为 0 的情况)**,然后取两个数中最大的,作为模式串往后滑动的位数。
|
|
||||||
|
|
||||||
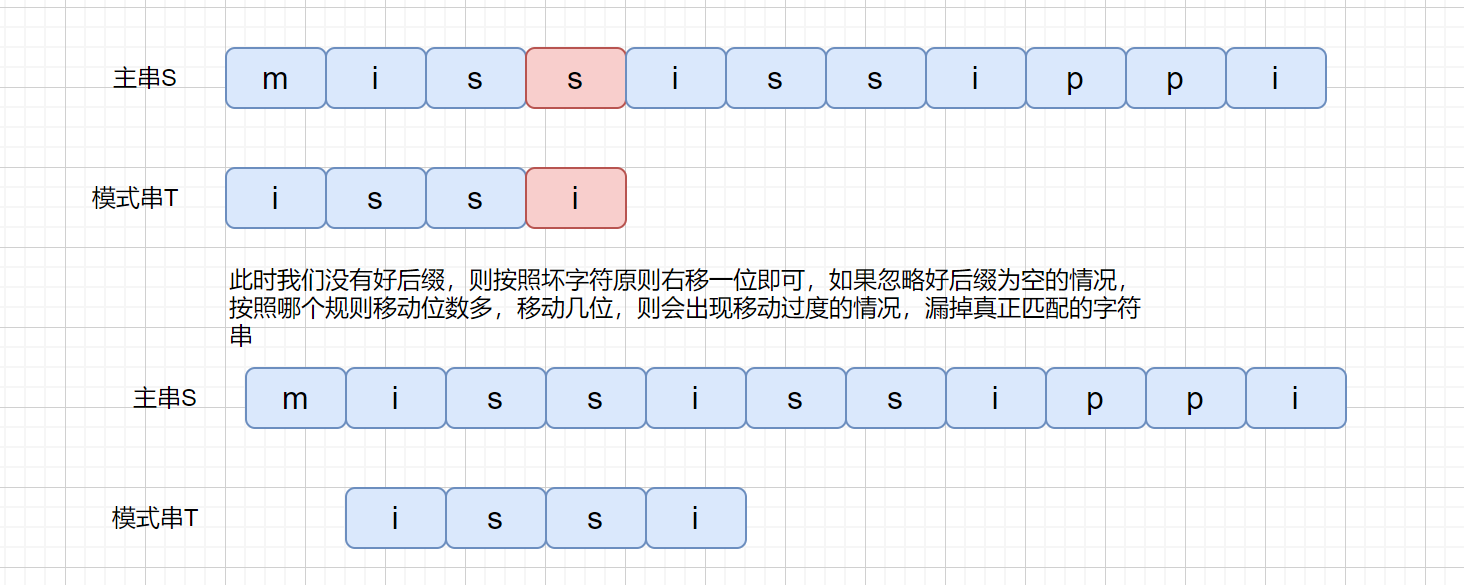
|
|
||||||
|
|
||||||
这破图画起来是真费劲啊。下面我们来看一下算法代码,代码有点长,我都标上了注释也在网站上 AC 了,如果各位感兴趣可以看一下,不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
char[] hay = haystack.toCharArray();
|
|
||||||
char[] need = needle.toCharArray();
|
|
||||||
int haylen = haystack.length();
|
|
||||||
int needlen = need.length;
|
|
||||||
return bm(hay,haylen,need,needlen);
|
|
||||||
}
|
|
||||||
//用来求坏字符情况下移动位数
|
|
||||||
private static void badChar(char[] b, int m, int[] bc) {
|
|
||||||
//初始化
|
|
||||||
for (int i = 0; i < 256; ++i) {
|
|
||||||
bc[i] = -1;
|
|
||||||
}
|
|
||||||
//m 代表模式串的长度,如果有两个 a,则后面那个会覆盖前面那个
|
|
||||||
for (int i = 0; i < m; ++i) {
|
|
||||||
int ascii = (int)b[i];
|
|
||||||
bc[ascii] = i;//下标
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//用来求好后缀条件下的移动位数
|
|
||||||
private static void goodSuffix (char[] b, int m, int[] suffix,boolean[] prefix) {
|
|
||||||
//初始化
|
|
||||||
for (int i = 0; i < m; ++i) {
|
|
||||||
suffix[i] = -1;
|
|
||||||
prefix[i] = false;
|
|
||||||
}
|
|
||||||
for (int i = 0; i < m - 1; ++i) {
|
|
||||||
int j = i;
|
|
||||||
int k = 0;
|
|
||||||
while (j >= 0 && b[j] == b[m-1-k]) {
|
|
||||||
--j;
|
|
||||||
++k;
|
|
||||||
suffix[k] = j + 1;
|
|
||||||
}
|
|
||||||
if (j == -1) prefix[k] = true;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
public static int bm (char[] a, int n, char[] b, int m) {
|
|
||||||
|
|
||||||
int[] bc = new int[256];//创建一个数组用来保存最右边字符的下标
|
|
||||||
badChar(b,m,bc);
|
|
||||||
//用来保存各种长度好后缀的最右位置的数组
|
|
||||||
int[] suffix_index = new int[m];
|
|
||||||
//判断是否是头部,如果是头部则true
|
|
||||||
boolean[] ispre = new boolean[m];
|
|
||||||
goodSuffix(b,m,suffix_index,ispre);
|
|
||||||
int i = 0;//第一个匹配字符
|
|
||||||
//注意结束条件
|
|
||||||
while (i <= n-m) {
|
|
||||||
int j;
|
|
||||||
//从后往前匹配,匹配失败,找到坏字符
|
|
||||||
for (j = m - 1; j >= 0; --j) {
|
|
||||||
if (a[i+j] != b[j]) break;
|
|
||||||
}
|
|
||||||
//模式串遍历完毕,匹配成功
|
|
||||||
if (j < 0) {
|
|
||||||
return i;
|
|
||||||
}
|
|
||||||
//下面为匹配失败时,如何处理
|
|
||||||
//求出坏字符规则下移动的位数,就是我们坏字符下标减最右边的下标
|
|
||||||
int x = j - bc[(int)a[i+j]];
|
|
||||||
int y = 0;
|
|
||||||
//好后缀情况,求出好后缀情况下的移动位数,如果不含有好后缀的话,则按照坏字符来
|
|
||||||
if (y < m-1 && m - 1 - j > 0) {
|
|
||||||
y = move(j, m, suffix_index,ispre);
|
|
||||||
}
|
|
||||||
//移动
|
|
||||||
i = i + Math.max(x,y);
|
|
||||||
|
|
||||||
}
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
// j代表坏字符的下标
|
|
||||||
private static int move (int j, int m, int[] suffix_index, boolean[] ispre) {
|
|
||||||
//好后缀长度
|
|
||||||
int k = m - 1 - j;
|
|
||||||
//如果含有长度为 k 的好后缀,返回移动位数,
|
|
||||||
if (suffix_index[k] != -1) return j - suffix_index[k] + 1;
|
|
||||||
//找头部为好后缀子串的最大长度,从长度最大的子串开始
|
|
||||||
for (int r = j + 2; r <= m-1; ++r) {
|
|
||||||
//如果是头部
|
|
||||||
if (ispre[m-r] == true) {
|
|
||||||
return r;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//如果没有发现好后缀匹配的串,或者头部为好后缀子串,则移动到 m 位,也就是匹配串的长度
|
|
||||||
return m;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
我们来理解一下我们代码中用到的两个数组,因为两个规则的移动位数,只与模式串有关,与主串无关,所以我们可以提前求出每种情况的移动情况,保存到数组中。
|
|
||||||
|
|
||||||
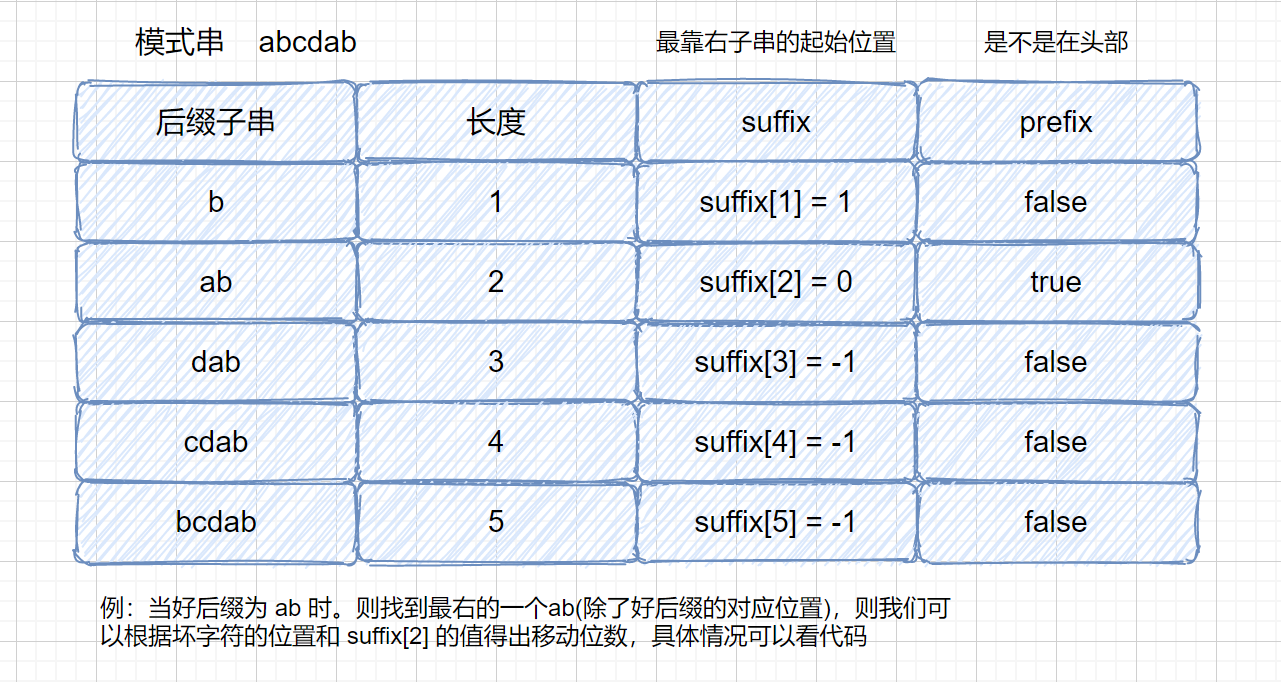
|
|
||||||
@ -1,363 +0,0 @@
|
|||||||
# 散列(哈希)表总结
|
|
||||||
|
|
||||||
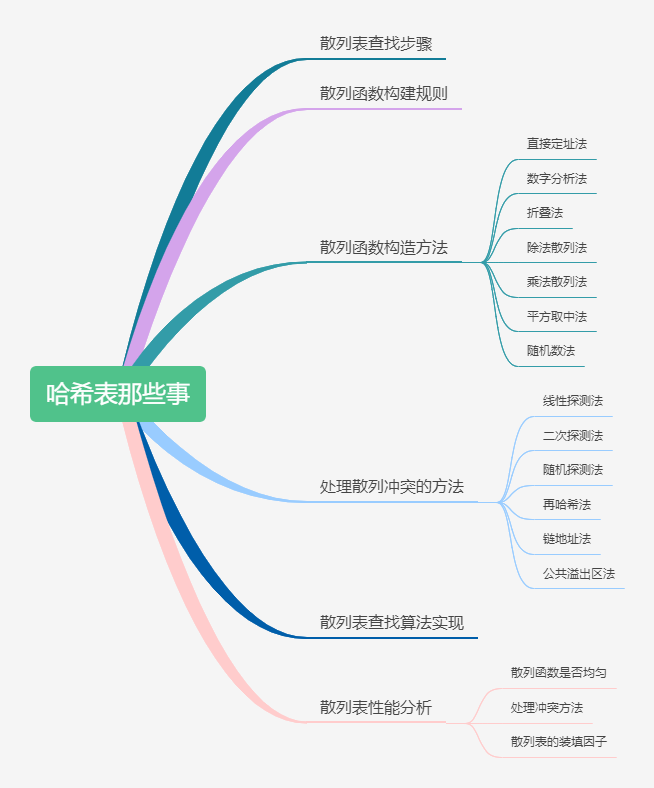
之前给大家介绍了**链表**,**栈和队列**今天我们来说一种新的数据结构散列(哈希)表,散列是应用非常广泛的数据结构,在我们的刷题过程中,散列表的出场率特别高。所以我们快来一起把散列表的内些事给整明白吧。文章框架如下
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
说散列表之前,我们先设想以下场景。
|
|
||||||
|
|
||||||
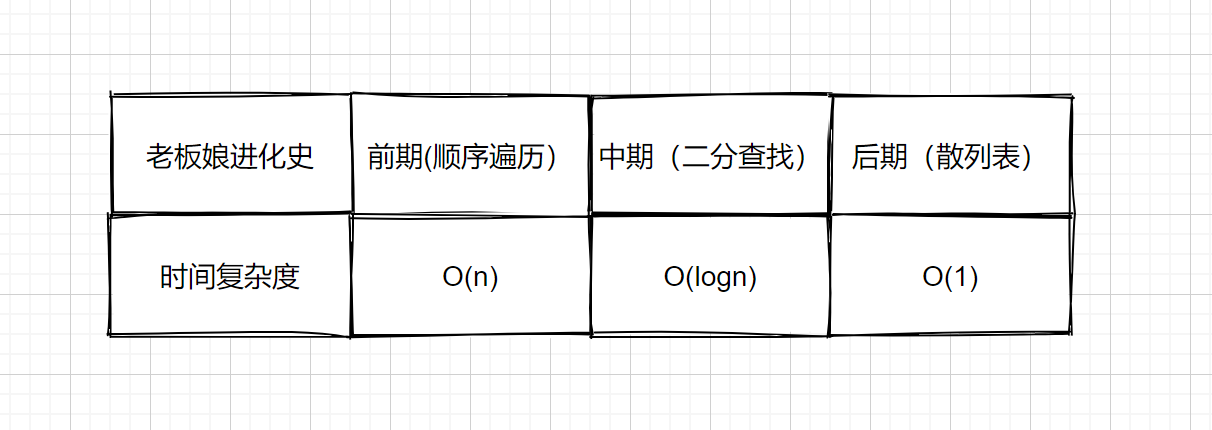
> 袁厨穿越回了古代,凭借从现代学习的做饭手艺,开了一个袁记菜馆,正值开业初期,店里生意十分火爆,但是顾客结账时就犯难了,每当结账的时候,老板娘总是按照菜单一个一个找价格(遍历查找),每次都要找半天,所以结账的地方总是排起长队,顾客们表示用户体验不咋滴。袁厨一想这不是办法啊,让顾客老是等着,太影响客户体验啦。所以袁厨就先把菜单按照首字母排序(二分查找),然后查找的时候根据首字母查找,这样结账的时候就能大大提高检索效率啦!但是呢?工作日顾客不多,老板娘完全应付的过来,但是每逢节假日,还是会排起长队。那么有没有什么更好的办法呢?对呀!我们把所有的价格都背下来不就可以了吗?每个菜的价格我们都了如指掌,结账的时候我们只需简单相加即可。所以袁厨和老板娘加班加点的进行背诵。下次再结账的时候一说吃了什么菜,我们立马就知道价格啦。自此以后收银台再也没有出现过长队啦,袁记菜馆开着开着一不小心就成了天下第一饭店了。
|
|
||||||
|
|
||||||
下面我们来看一下袁记菜馆老板娘进化史。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
上面的后期结账的过程则模拟了我们的散列表查找,那么在计算机中是如何使用进行查找的呢?
|
|
||||||
|
|
||||||
### 散列表查找步骤
|
|
||||||
|
|
||||||
散列表-------最有用的基本数据结构之一。是根据关键码的值儿直接进行访问的数据结构,散列表的实现常常叫做**散列(hasing)**。散列是一种用于以**常数平均时间**执行插入、删除和查找的技术,下面我们来看一下散列过程。
|
|
||||||
|
|
||||||
我们的整个散列过程主要分为两步
|
|
||||||
|
|
||||||
(1)通过**散列函数**计算记录的散列地址,并按此**散列地址**存储该记录。就好比麻辣鱼我们就让它在川菜区,糖醋鱼,我们就让它在鲁菜区。但是我们需要注意的是,无论什么记录我们都需要用**同一个散列函数**计算地址,再存储。
|
|
||||||
|
|
||||||
(2)当我们查找时,我们通过**同样的散列函数**计算记录的散列地址,按此散列地址访问该记录。因为我们存和取得时候用的都是一个散列函数,因此结果肯定相同。
|
|
||||||
|
|
||||||
刚才我们在散列过程中提到了散列函数,那么散列函数是什么呢?
|
|
||||||
|
|
||||||
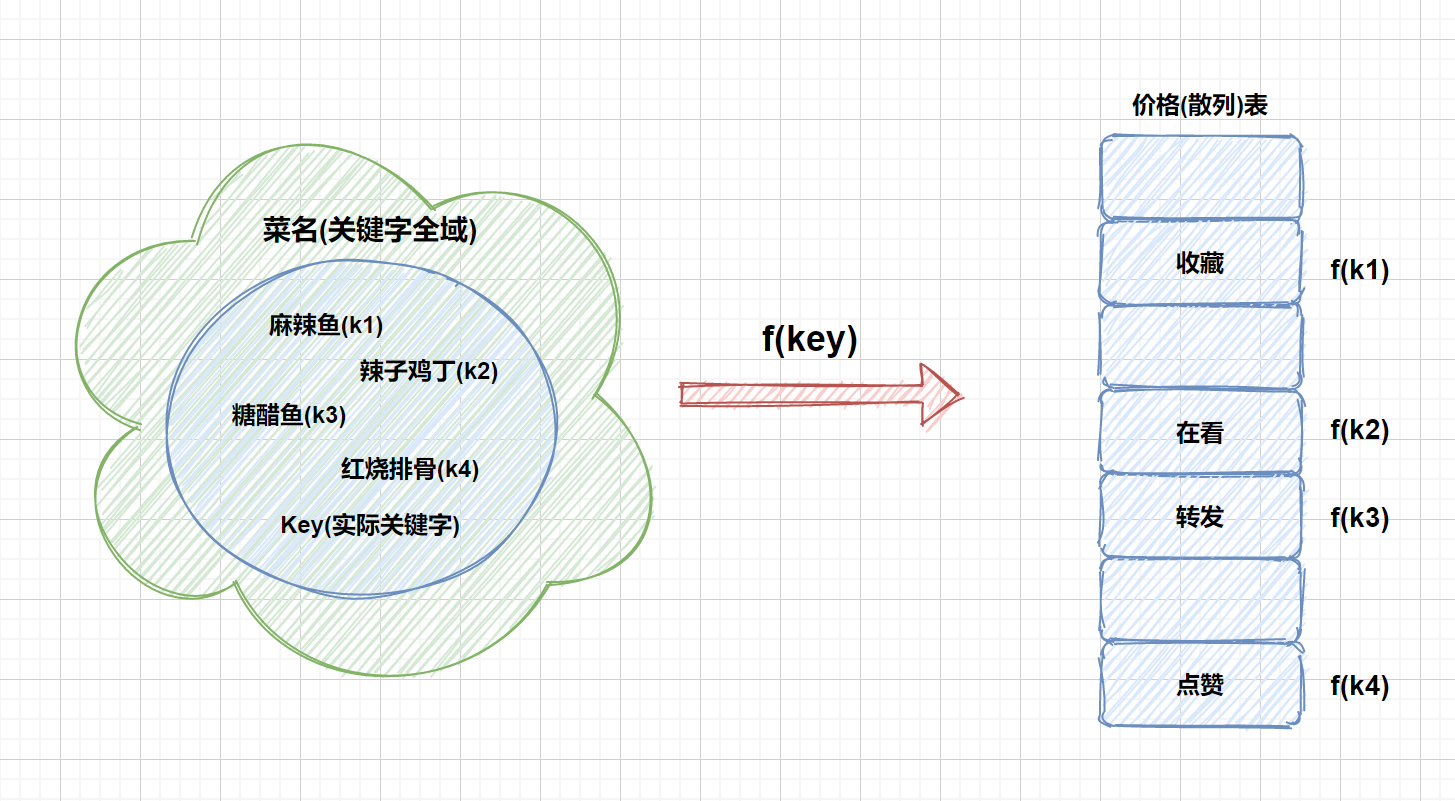
我们假设某个函数为 **f**,使得
|
|
||||||
|
|
||||||
**存储位置 = f (关键字)**
|
|
||||||
|
|
||||||
**输入:关键字** **输出:存储位置(散列地址)**
|
|
||||||
|
|
||||||
那样我们就能通过查找关键字**不需要比较**就可获得需要的记录的存储位置。这种存储技术被称为散列技术。散列技术是在通过记录的存储位置和它的关键字之间建立一个确定的对应关系 **f** ,使得每个关键字 **key** 都对应一个存储位置 **f(key)**。见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
这里的 **f** 就是我们所说的散列函数(哈希)函数。我们利用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间就是我们本文的主人公------**散列(哈希)表**
|
|
||||||
|
|
||||||
上图为我们描述了用散列函数将关键字映射到散列表,但是大家有没有考虑到这种情况,那就是将关键字映射到同一个槽中的情况,即 **f(k4) = f(k3)** 时。这种情况我们将其称之为**冲突**,**k3** 和 **k4**则被称之为散列函数 **f** 的**同义词**,如果产生这种情况,则会让我们查找错误。幸运的是我们能找到有效的方法解决冲突。
|
|
||||||
|
|
||||||
首先我们可以对哈希函数下手,我们可以精心设计哈希函数,让其尽可能少的产生冲突,所以我们创建哈希函数时应遵循以下规则
|
|
||||||
|
|
||||||
(1)**必须是一致的**,假设你输入辣子鸡丁时得到的是**在看**,那么每次输入辣子鸡丁时,得到的也必须为**在看**。如果不是这样,散列表将毫无用处。
|
|
||||||
|
|
||||||
(2)**计算简单**,假设我们设计了一个算法,可以保证所有关键字都不会冲突,但是这个算法计算复杂,会耗费很多时间,这样的话就大大降低了查找效率,反而得不偿失。所以咱们**散列函数的计算时间不应该超过其他查找技术与关键字的比较时间**,不然的话我们干嘛不使用其他查找技术呢?
|
|
||||||
|
|
||||||
(3)**散列地址分布均匀**我们刚才说了冲突的带来的问题,所以我们最好的办法就是让**散列地址尽量均匀分布在存储空间中**,这样即保证空间的有效利用,又减少了处理冲突而消耗的时间。
|
|
||||||
|
|
||||||
现在我们已经对散列表,散列函数等知识有所了解啦,那么我们来看几种常用的散列函数构造规则。这些方法的共同点为都是将原来的数字按某种规律变成了另一个数字。
|
|
||||||
|
|
||||||
### 散列函数构造方法
|
|
||||||
|
|
||||||
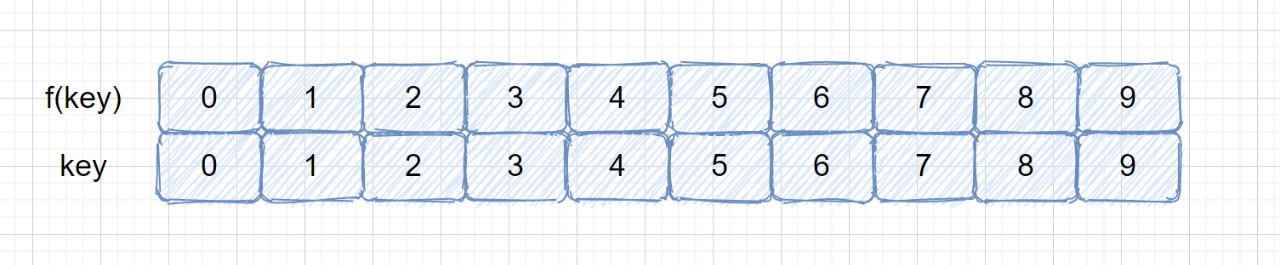
#### 直接定址法
|
|
||||||
|
|
||||||
如果我们对盈利为0-9的菜品设计哈希表,我们则直接可以根据作为地址,则 **f(key) = key**;
|
|
||||||
|
|
||||||
即下面这种情况。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
有没有感觉上面的图很熟悉,没错我们经常用的数组其实就是一张哈希表,关键码就是数组的索引下标,然后我们通过下标直接访问数组中的元素。
|
|
||||||
|
|
||||||
另外我们假设每道菜的成本为50块,那我们还可以根据盈利+成本来作为地址,那么则 f(key) = key + 50。也就是说我们可以根据线性函数值作为散列地址。
|
|
||||||
|
|
||||||
**f(key) = a * key + b** **a,b均为常数**
|
|
||||||
|
|
||||||
优点:简单、均匀、无冲突。
|
|
||||||
|
|
||||||
应用场景:需要事先知道关键字的分布情况,适合查找表较小且连续的情况
|
|
||||||
|
|
||||||
#### 数字分析法
|
|
||||||
|
|
||||||
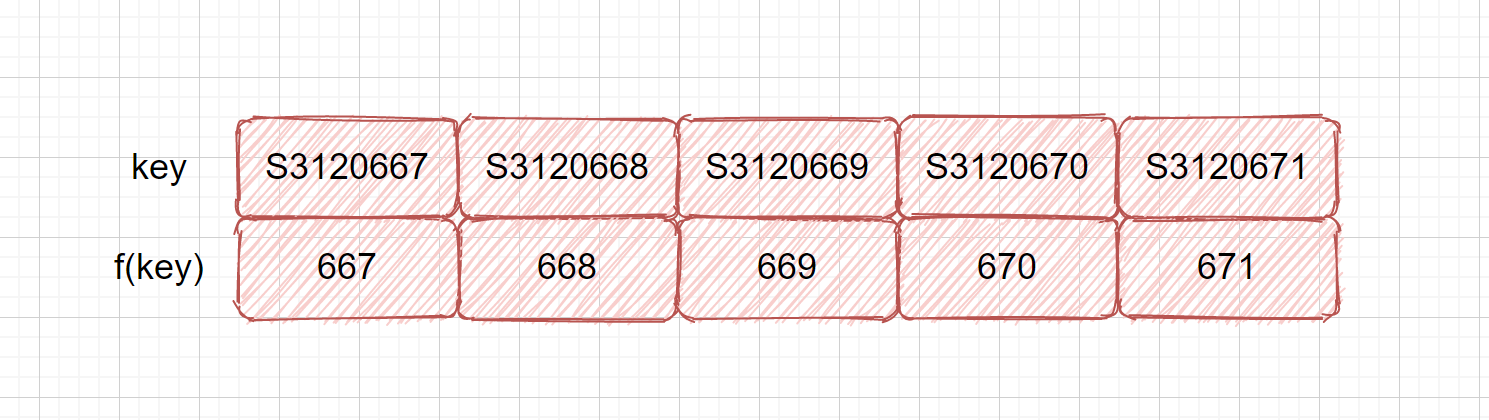
该方法也是十分简单的方法,就是分析我们的关键字,取其中一段,或对其位移,叠加,用作地址。比如我们的学号,前 6 位都是一样的,但是后面 3 位都不相同,我们则可以用学号作为键,后面的 3 位做为我们的散列地址。如果我们这样还是容易产生冲突,则可以对抽取数字再进行处理。我们的目的只有一个,提供一个散列函数将关键字合理的分配到散列表的各位置。这里我们提到了一种新的方式,抽取,这也是在散列函数中经常用到的手段。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
优点:简单、均匀、适用于关键字位数较大的情况
|
|
||||||
|
|
||||||
应用场景:关键字位数较大,知道关键字分布情况且关键字的若干位较均匀
|
|
||||||
|
|
||||||
#### 折叠法
|
|
||||||
|
|
||||||
其实这个方法也很简单,也是处理我们的关键字然后用作我们的散列地址,主要思路是将关键字从左到右分割成位数相等的几部分,然后叠加求和,并按散列表表长,取后几位作为散列地址。
|
|
||||||
|
|
||||||
比如我们的关键字是123456789,则我们分为三部分 123 ,456 ,789 然后将其相加得 1368 然后我们再取其后三位 368 作为我们的散列地址。
|
|
||||||
|
|
||||||
优点:事先不需要知道关键字情况
|
|
||||||
|
|
||||||
应用场景:适合关键字位数较多的情况
|
|
||||||
|
|
||||||
#### 除法散列法
|
|
||||||
|
|
||||||
在用来设计散列函数的除法散列法中,通过取 key 除以 p 的余数,将关键字映射到 p 个槽中的某一个上,对于散列表长度为 m 的散列函数公式为
|
|
||||||
|
|
||||||
**f(k) = k mod p (p <= m)**
|
|
||||||
|
|
||||||
例如,如果散列表长度为 12,即 m = 12 ,我们的参数 p 也设为12,**那 k = 100时 f(k) = 100 % 12 = 4**
|
|
||||||
|
|
||||||
由于只需要做一次除法操作,所以除法散列法是非常快的。
|
|
||||||
|
|
||||||
由上面的公式可以看出,该方法的重点在于 p 的取值,如果 p 值选的不好,就可能会容易产生同义词。见下面这种情况。我们哈希表长度为6,我们选择6为p值,则有可能产生这种情况,所有关键字都得到了0这个地址数。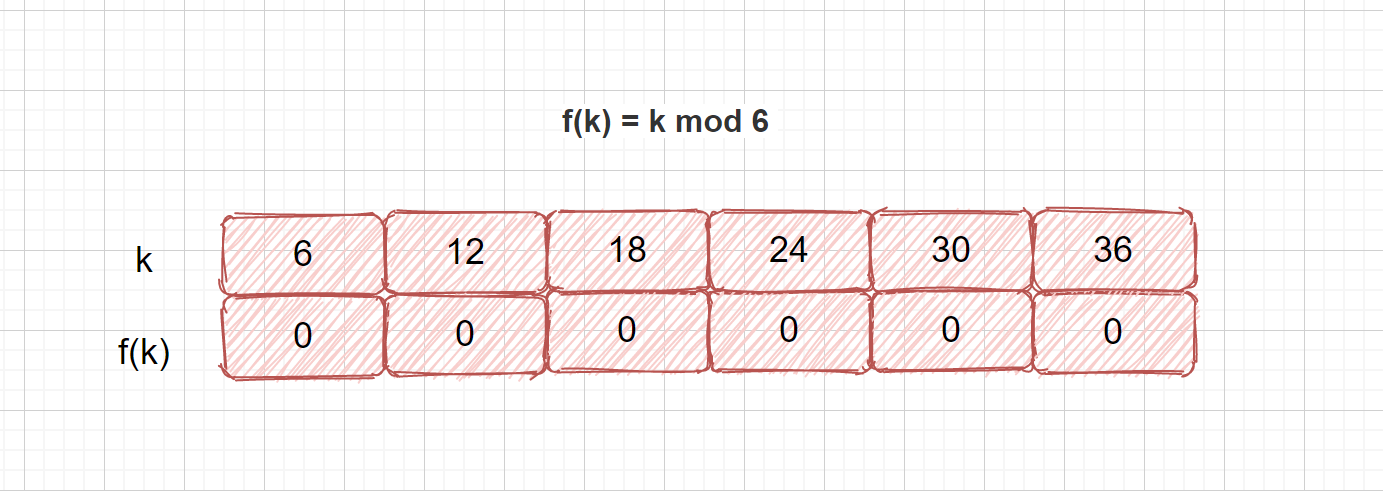
|
|
||||||
|
|
||||||
那我们在选用除法散列法时选取 p 值时应该遵循怎样的规则呢?
|
|
||||||
|
|
||||||
- m 不应为 2 的幂,因为如果 m = 2^p ,则 f(k) 就是 k 的 p 个最低位数字。例 12 % 8 = 4 ,12的二进制表示位1100,后三位为100。
|
|
||||||
- 若散列表长为 m ,通常 p 为 小于或等于表长(最好接近m)的最小质数或不包含小于 20 质因子的合数。
|
|
||||||
|
|
||||||
> **合数:**合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。
|
|
||||||
>
|
|
||||||
> **质因子**:质因子(或质因数)在数论里是指能整除给定正整数的质数。
|
|
||||||
|
|
||||||
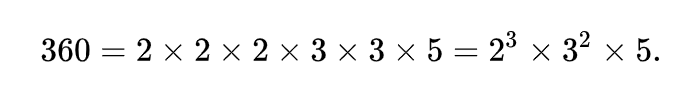
|
|
||||||
|
|
||||||
这里的2,3,5为质因子
|
|
||||||
|
|
||||||
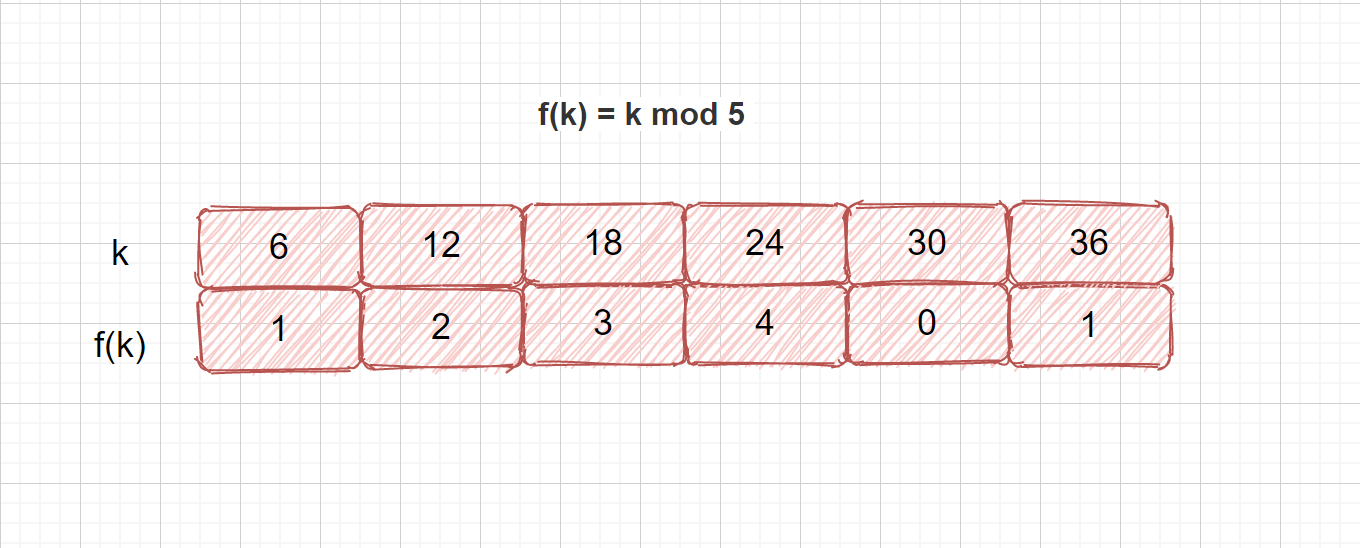
还是上面的例子,我们根据规则选择 5 为 p 值,我们再来看。这时我们发现只有 6 和 36 冲突,相对来说就好了很多。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
优点:计算效率高,灵活
|
|
||||||
|
|
||||||
应用场景:不知道关键字分布情况
|
|
||||||
|
|
||||||
#### 乘法散列法
|
|
||||||
|
|
||||||
构造散列函数的乘法散列法主要包含两个步骤
|
|
||||||
|
|
||||||
- 用关键字 k 乘上常数 A(0 < A < 1),并提取 k A 的小数部分
|
|
||||||
- 用 m 乘以这个值,再向下取整
|
|
||||||
|
|
||||||
散列函数为
|
|
||||||
|
|
||||||
**f (k) = ⌊ m(kA mod 1) ⌋**
|
|
||||||
|
|
||||||
这里的 **kA mod 1** 的含义是取 keyA 的小数部分,即 **kA - ⌊kA⌋** 。
|
|
||||||
|
|
||||||
优点:对 m 的选择不是特别关键,一般选择它为 2 的某个幂次(m = 2 ^ p ,p为某个整数)
|
|
||||||
|
|
||||||
应用场景:不知道关键字情况
|
|
||||||
|
|
||||||
#### 平方取中法
|
|
||||||
|
|
||||||
这个方法就比较简单了,假设关键字是 321,那么他的平方就是 103041,再抽取中间的 3 位就是 030 或 304 用作散列地址。再比如关键字是 1234 那么它的平方就是 1522756 ,抽取中间 3 位就是 227 用作散列地址.
|
|
||||||
|
|
||||||
优点:灵活,适用范围广泛
|
|
||||||
|
|
||||||
适用场景:不知道关键字分布,而位数又不是很大的情况。
|
|
||||||
|
|
||||||
#### 随机数法
|
|
||||||
|
|
||||||
故名思意,取关键字的随机函数值为它的散列地址。也就是 **f(key) = random(key)**。这里的random是 随机函数。
|
|
||||||
|
|
||||||
优点:易实现
|
|
||||||
|
|
||||||
适用场景:关键字的长度不等时
|
|
||||||
|
|
||||||
上面我们的例子都是通过数字进行举例,那么如果是字符串可不可以作为键呢?当然也是可以的,各种各样的符号我们都可以转换成某种数字来对待,比如我们经常接触的ASCII 码,所以是同样适用的。
|
|
||||||
|
|
||||||
以上就是常用的散列函数构造方法,其实他们的中心思想是一致的,将关键字经过加工处理之后变成另外一个数字,而这个数字就是我们的存储位置,是不是有一种间谍传递情报的感觉。
|
|
||||||
|
|
||||||
一个好的哈希函数可以帮助我们尽可能少的产生冲突,但是也不能完全避免产生冲突,那么遇到冲突时应该怎么做呢?下面给大家带来几种常用的处理散列冲突的方法。
|
|
||||||
|
|
||||||
### 处理散列冲突的方法
|
|
||||||
|
|
||||||
我们在使用 hash 函数之后发现关键字 key1 不等于 key2 ,但是 f(key1) = f(key2),即有冲突,那么该怎么办呢?不急我们慢慢往下看。
|
|
||||||
|
|
||||||
#### 开放地址法
|
|
||||||
|
|
||||||
了解开放地址法之前我们先设想以下场景。
|
|
||||||
|
|
||||||
> 袁记菜馆内,铃铃铃,铃铃铃 电话铃响了
|
|
||||||
>
|
|
||||||
> 大鹏:老袁,给我订个包间,我今天要去带几个客户去你那谈生意。
|
|
||||||
>
|
|
||||||
> 袁厨:大鹏啊,你常用的那个包间被人订走啦。
|
|
||||||
>
|
|
||||||
> 大鹏:老袁你这不仗义呀,咋没给我留住呀,那你给我找个**空房间**吧。
|
|
||||||
>
|
|
||||||
> 袁厨:好滴老哥
|
|
||||||
|
|
||||||
哦,穿越回古代就没有电话啦,那看来穿越的时候得带着几个手机了。
|
|
||||||
|
|
||||||
上面的场景其实就是一种处理冲突的方法-----开放地址法
|
|
||||||
|
|
||||||
**开放地址法**就是一旦发生冲突,就去寻找下一个空的散列地址,只要列表足够大,空的散列地址总能找到,并将记录存入,为了使用开放寻址法插入一个元素,需要连续地检查散列表,或称为**探查**,我们常用的有**线性探测,二次探测,随机探测**。
|
|
||||||
|
|
||||||
##### 线性探测法
|
|
||||||
|
|
||||||
下面我们先来看一下线性探测,公式:
|
|
||||||
|
|
||||||
> **f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
|
||||||
|
|
||||||
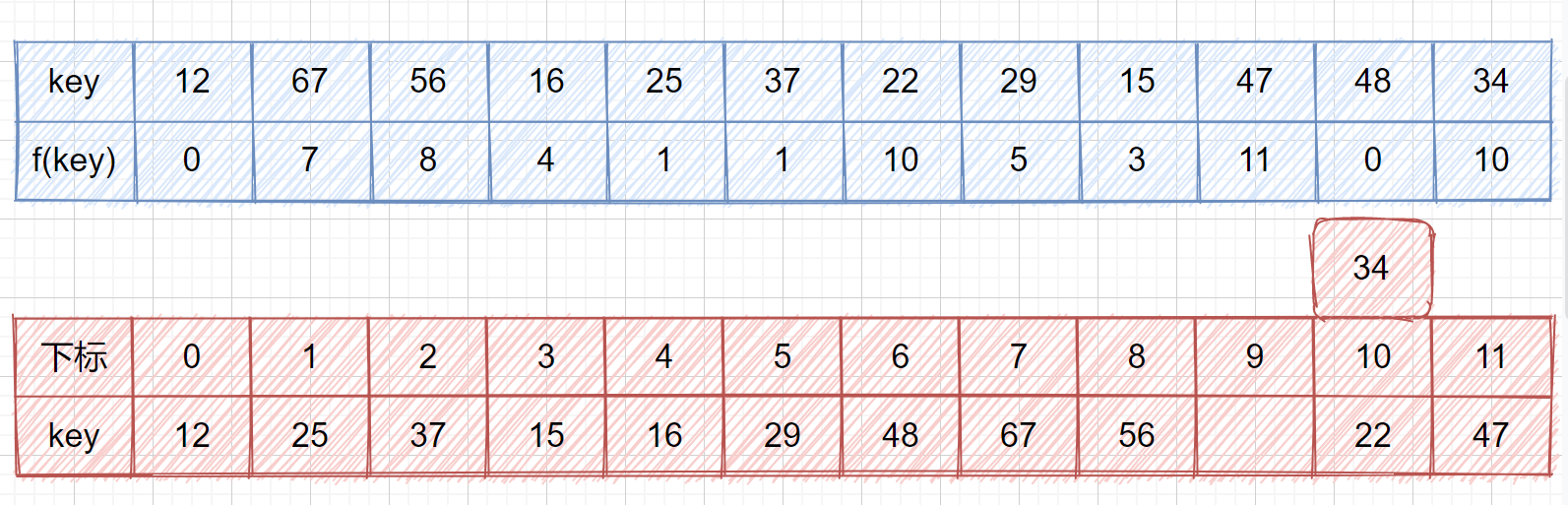
我们来看一个例子,我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为12,我们再用散列函数 **f(key) = key mod 12。**
|
|
||||||
|
|
||||||
我们求出每个 key 的 f(key)见下表
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们查看上表发现,前五位的 **f(key)** 都不相同,即没有冲突,可以直接存入,但是到了第六位 **f(37) = f(25) = 1**,那我们就需要利用上面的公式 **f(37) = f (f(37) + 1 ) mod 12 = 2**,这其实就是我们的订包间的做法。下面我们看一下将上面的所有数存入哈希表是什么情况吧。
|
|
||||||
|
|
||||||
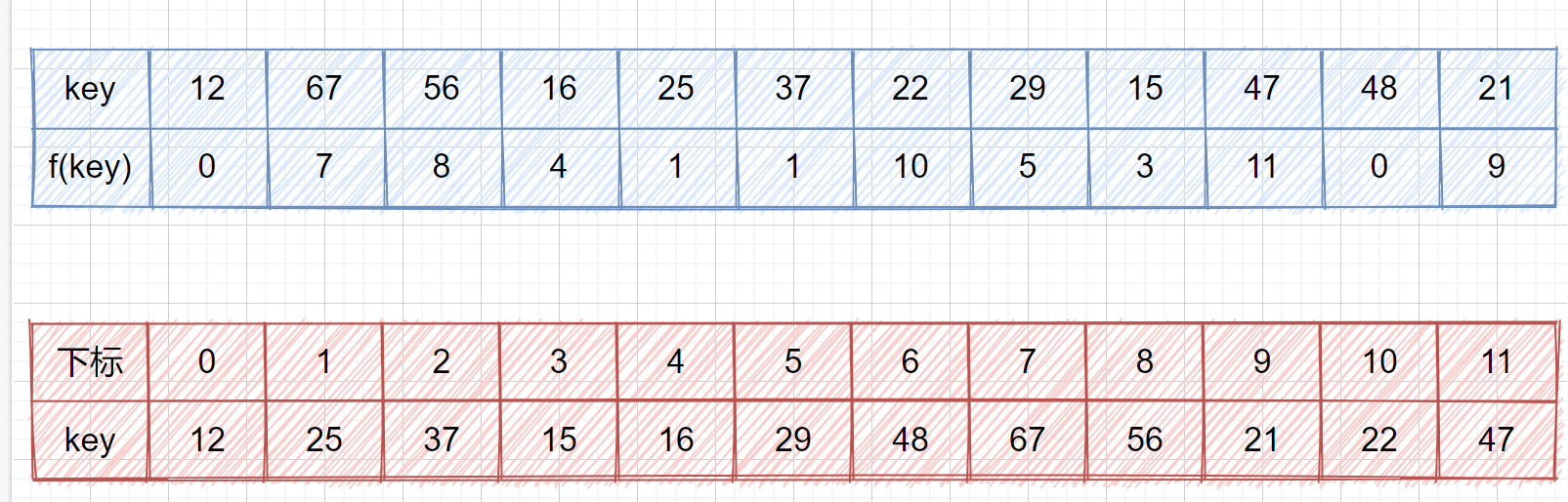
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们把这种解决冲突的开放地址法称为**线性探测法**。下面我们通过视频来模拟一下线性探测法的存储过程。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
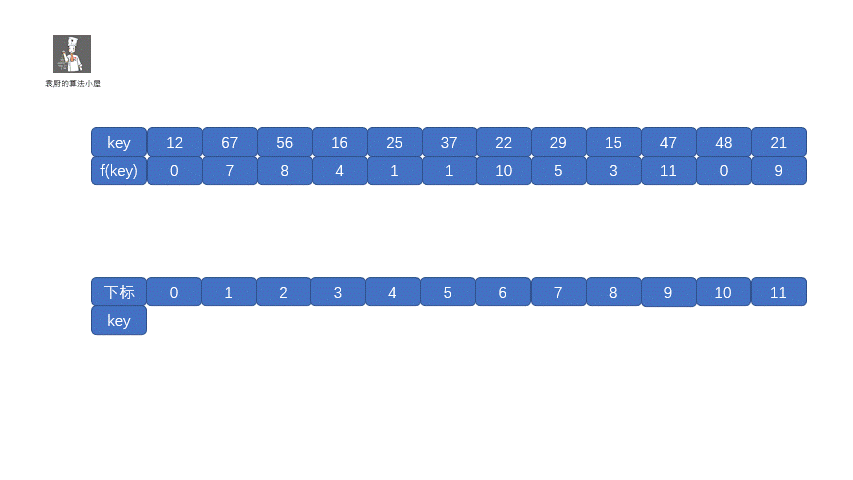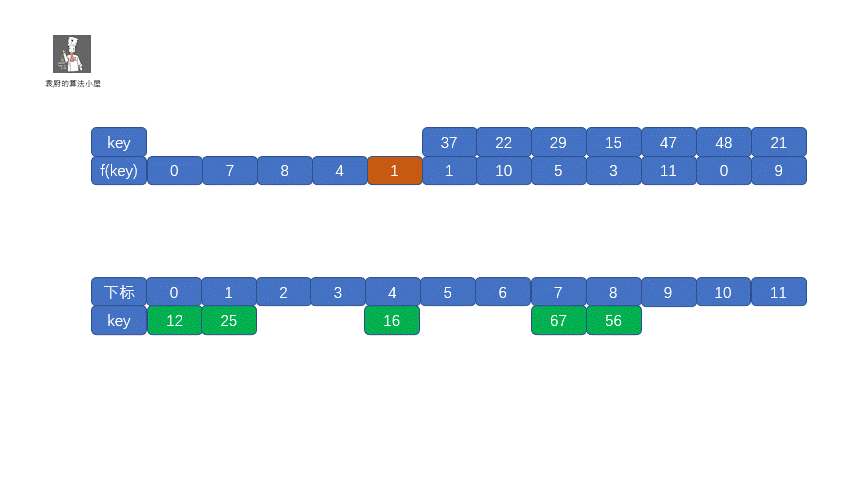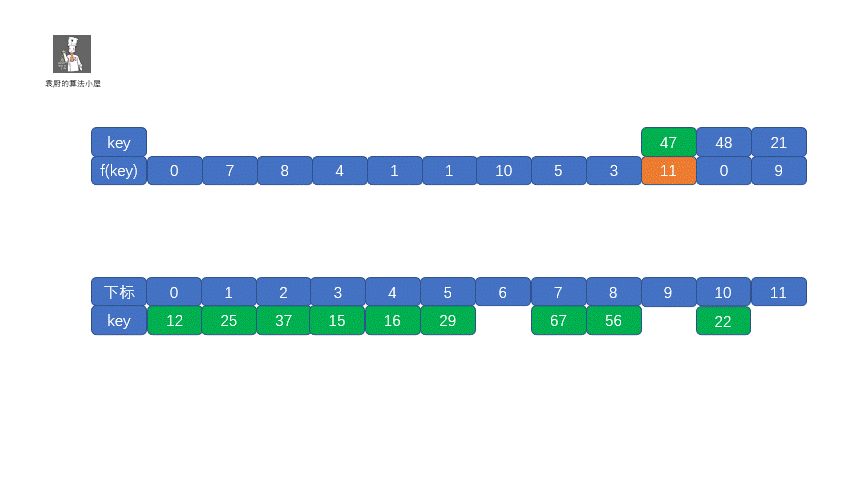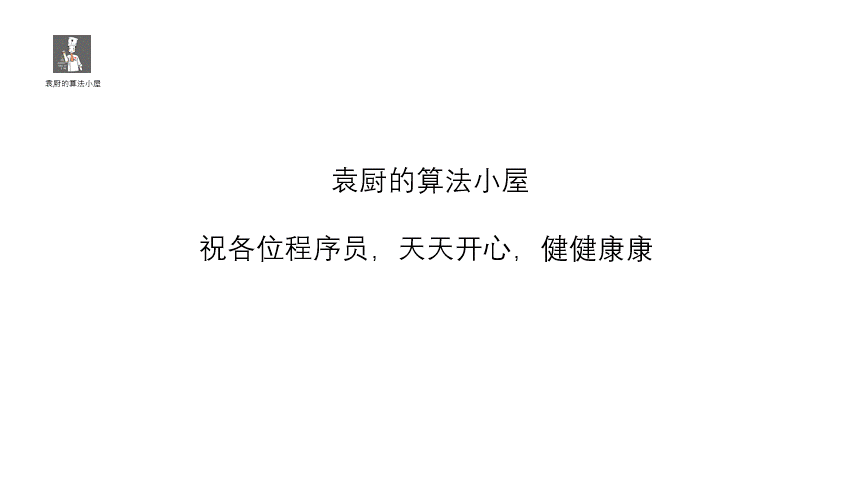
|
|
||||||
|
|
||||||
另外我们在解决冲突的时候,会遇到 48 和 37 虽然不是同义词,却争夺一个地址的情况,我们称其为**堆积**。因为堆积使得我们需要不断的处理冲突,插入和查找效率都会大大降低。
|
|
||||||
|
|
||||||
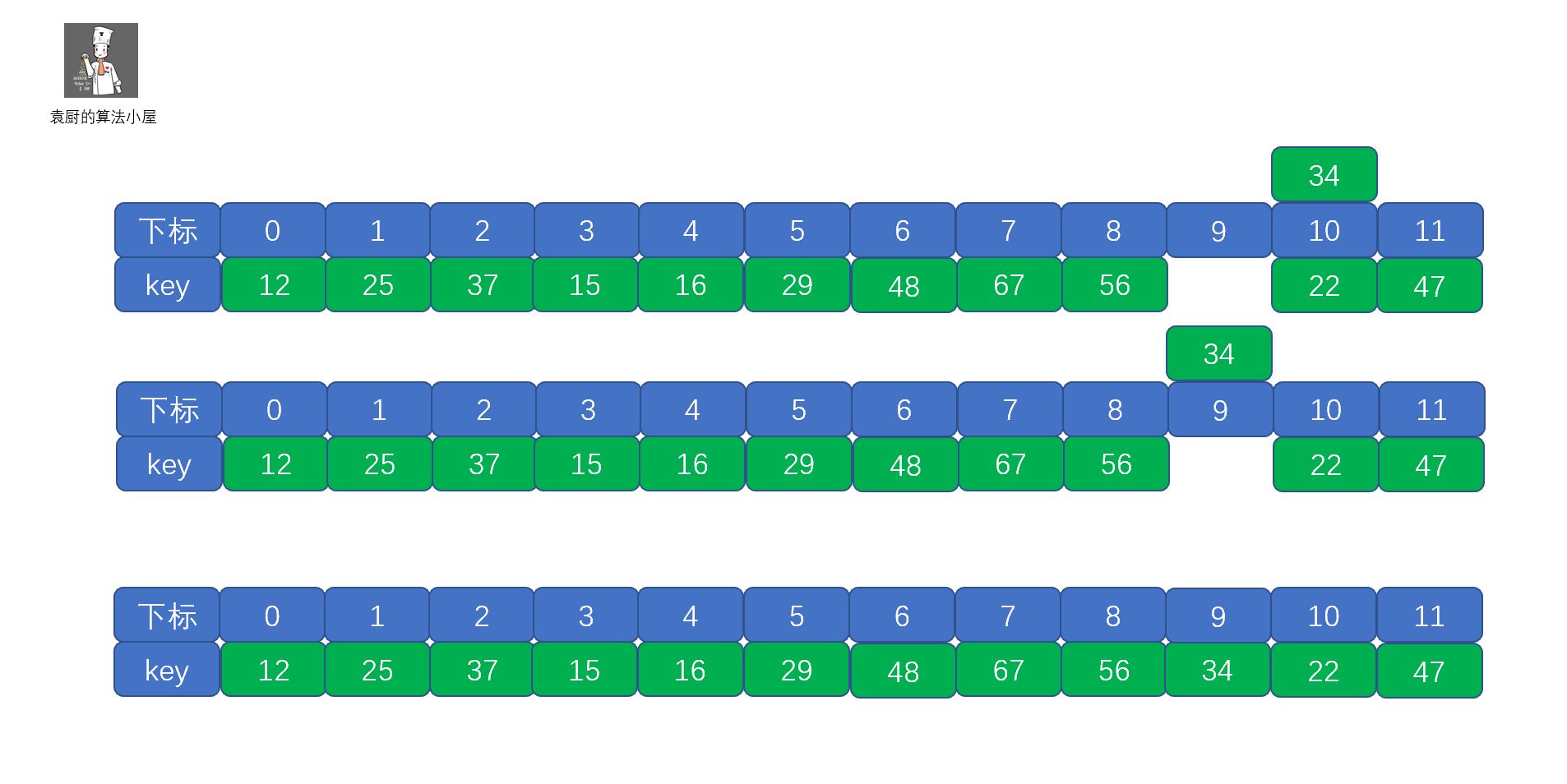
通过上面的视频我们应该了解了线性探测的执行过程了,那么我们考虑一下这种情况,若是我们的最后一位不为21,为 34 时会有什么事情发生呢?
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时他第一次会落在下标为 10 的位置,那么如果继续使用线性探测的话,则需要通过不断取余后得到结果,数据量小还好,要是很大的话那也太慢了吧,但是明明他的前面就有一个空房间呀,如果向前移动只需移动一次即可。不要着急,前辈们已经帮我们想好了解决方法
|
|
||||||
|
|
||||||
##### 二次探测法
|
|
||||||
|
|
||||||
其实理解了我们的上个例子之后,这个一下就能整明白了,根本不用费脑子,这个方法就是更改了一下di的取值
|
|
||||||
|
|
||||||
> **线性探测: f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
|
||||||
>
|
|
||||||
> **二次探测:** **f,(key) = ( f(key) + di ) MOD m(di =1^2 , -1^2 , 2^2 , -2^2 .... q^2, -q^2, q<=m/2)**
|
|
||||||
|
|
||||||
**注:这里的是 -1^2 为负值 而不是 (-1)^2**
|
|
||||||
|
|
||||||
所以对于我们的34来说,当di = -1时,就可以找到空位置了。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
二次探测法的目的就是为了不让关键字聚集在某一块区域。另外还有一种有趣的方法,位移量采用随机函数计算得到,接着往下看吧.
|
|
||||||
|
|
||||||
##### 随机探测法
|
|
||||||
|
|
||||||
大家看到这是不又有新问题了,刚才我们在散列函数构造规则的第一条中说
|
|
||||||
|
|
||||||
> (1)**必须是一致的**,假设你输入辣子鸡丁时得到的是**在看**,那么每次输入辣子鸡丁时,得到的也必须为**在看**。如果不是这样,散列表将毫无用处。
|
|
||||||
|
|
||||||
咦?怎么又是**在看**哈哈,那么问题来了,我们使用随机数作为他的偏移量,那么我们查找的时候岂不是查不到了?因为我们 di 是随机生成的呀,这里的随机其实是伪随机数,伪随机数含义为,我们设置**随机种子**相同,则不断调用随机函数可以生成**不会重复的数列**,我们在查找时,**用同样的随机种子**,**它每次得到的数列是相同的**,那么相同的 di 就能得到**相同的散列地址**。
|
|
||||||
|
|
||||||
> 随机种子(Random Seed)是计算机专业术语,一种以随机数作为对象的以真随机数(种子)为初始条件的随机数。一般计算机的随机数都是伪随机数,以一个真随机数(种子)作为初始条件,然后用一定的算法不停迭代产生随机数
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
通过上面的测试是不是一下就秒懂啦,为什么我们可以使用随机数作为它的偏移量,理解那句,相同的随机种子,他每次得到的数列是相同的。
|
|
||||||
|
|
||||||
下面我们再来看一下其他的函数处理散列冲突的方法
|
|
||||||
|
|
||||||
#### 再哈希法
|
|
||||||
|
|
||||||
这个方法其实也特别简单,利用不同的哈希函数再求得一个哈希地址,直到不出现冲突为止。
|
|
||||||
|
|
||||||
> **f,(key) = RH,( key ) (i = 1,2,3,4.....k)**
|
|
||||||
|
|
||||||
这里的RH,就是不同的散列函数,你可以把我们之前说过的那些散列函数都用上,每当发生冲突时就换一个散列函数,相信总有一个能够解决冲突的。这种方法能使关键字不产生聚集,但是代价就是增加了计算时间。是不是很简单啊。
|
|
||||||
|
|
||||||
#### 链地址法
|
|
||||||
|
|
||||||
下面我们再设想以下情景。
|
|
||||||
|
|
||||||
> 袁记菜馆内,铃铃铃,铃铃铃电话铃又响了,那个大鹏又来订房间了。
|
|
||||||
>
|
|
||||||
> 大鹏:老袁啊,我一会去你那吃个饭,还是上回那个包间
|
|
||||||
>
|
|
||||||
> 袁厨:大鹏你下回能不能早点说啊,又没人订走了,这回是老王订的
|
|
||||||
>
|
|
||||||
> 大鹏:老王这个老东西啊,反正也是熟人,你再给我整个桌子,我拼在他后面吧
|
|
||||||
|
|
||||||
不好意思啊各位同学,信鸽最近太贵了还没来得及买。上面的情景就是模拟我们的新的处理冲突的方法链地址法。
|
|
||||||
|
|
||||||
上面我们都是遇到冲突之后,就换地方。那么我们有没有不换地方的办法呢?那就是我们现在说的链地址法。
|
|
||||||
|
|
||||||
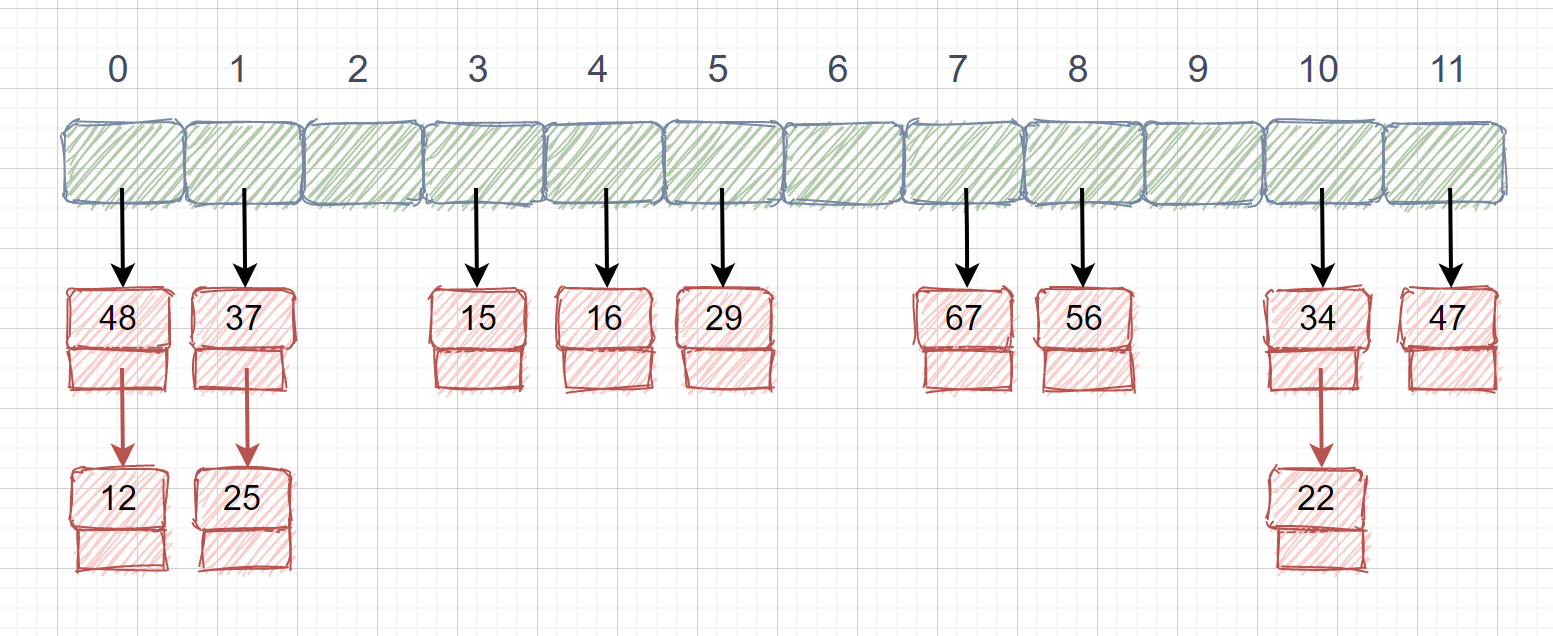
还记得我们说过得同义词吗?就是 key 不同 f(key) 相同的情况,我们将这些同义词存储在一个单链表中,这种表叫做同义词子表,散列表中只存储同义词子表的头指针。我们还是用刚才的例子,关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为12,我们再用散列函数 **f(key) = key mod 12。**我们用了链地址法之后就再也不存在冲突了,无论有多少冲突,我们只需在同义词子表中添加结点即可。下面我们看下链地址法的存储情况。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
链地址法虽然能够不产生冲突,但是也带来了查找时需要遍历单链表的性能消耗,有得必有失嘛。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
#### 公共溢出区法
|
|
||||||
|
|
||||||
下面我们再来看一种新的方法,这回大鹏又要来吃饭了。
|
|
||||||
|
|
||||||
> 袁记菜馆内.....
|
|
||||||
>
|
|
||||||
> 袁厨:呦,这是什么风把你给刮来了,咋没开你的大奔啊。
|
|
||||||
>
|
|
||||||
> 大鹏:哎呀妈呀,别那么多废话了,我快饿死了,你快给我找个位置,我要吃点饭。
|
|
||||||
>
|
|
||||||
> 袁厨:你来的,太不巧了,咱们的店已经满了,你先去旁边的小屋看会电视,等有空了我再叫你。小屋里面还有几个和你一样来晚的,你们一起看吧。
|
|
||||||
>
|
|
||||||
> 大鹏:电视?看电视?
|
|
||||||
|
|
||||||
上面得情景就是模拟我们的公共溢出区法,这也是很好理解的,你不是冲突吗?那冲突的各位我先给你安排个地方呆着,这样你就有地方住了。我们为所有冲突的关键字建立了一个公共的溢出区来存放。
|
|
||||||
|
|
||||||
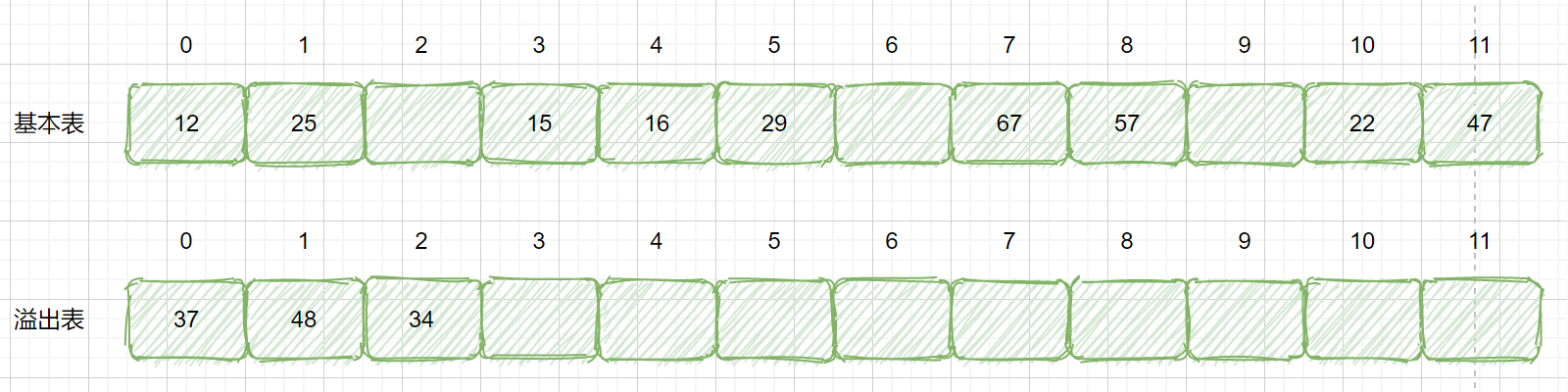
|
|
||||||
|
|
||||||
那么我们怎么进行查找呢?我们首先通过散列函数计算出散列地址后,先于基本表对比,如果不相等再到溢出表去顺序查找。这种解决冲突的方法,对于冲突很少的情况性能还是非常高的。
|
|
||||||
|
|
||||||
### 散列表查找算法(线性探测法)
|
|
||||||
|
|
||||||
下面我们来看一下散列表查找算法的实现
|
|
||||||
|
|
||||||
首先需要定义散列列表的结构以及一些相关常数,其中elem代表散列表数据存储数组,count代表的是当前插入元素个数,size代表哈希表容量,NULLKEY散列表初始值,然后我们如果查找成功就返回索引,如果不存在该元素就返回元素不存在。
|
|
||||||
|
|
||||||
我们将哈希表初始化,为数组元素赋初值。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
插入操作的具体步骤:
|
|
||||||
|
|
||||||
(1)通过哈希函数(除法散列法),将 key 转化为数组下标
|
|
||||||
|
|
||||||
(2)如果该下标中没有元素,则插入,否则说明有冲突,则利用线性探测法处理冲突。详细步骤见注释
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
查找操作的具体步骤:
|
|
||||||
|
|
||||||
(1)通过哈希函数(同插入时一样),将 key 转成数组下标
|
|
||||||
|
|
||||||
(2)通过数组下标找到 key值,如果 key 一致,则查找成功,否则利用线性探测法继续查找。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
下面我们来看一下完整代码
|
|
||||||
|
|
||||||
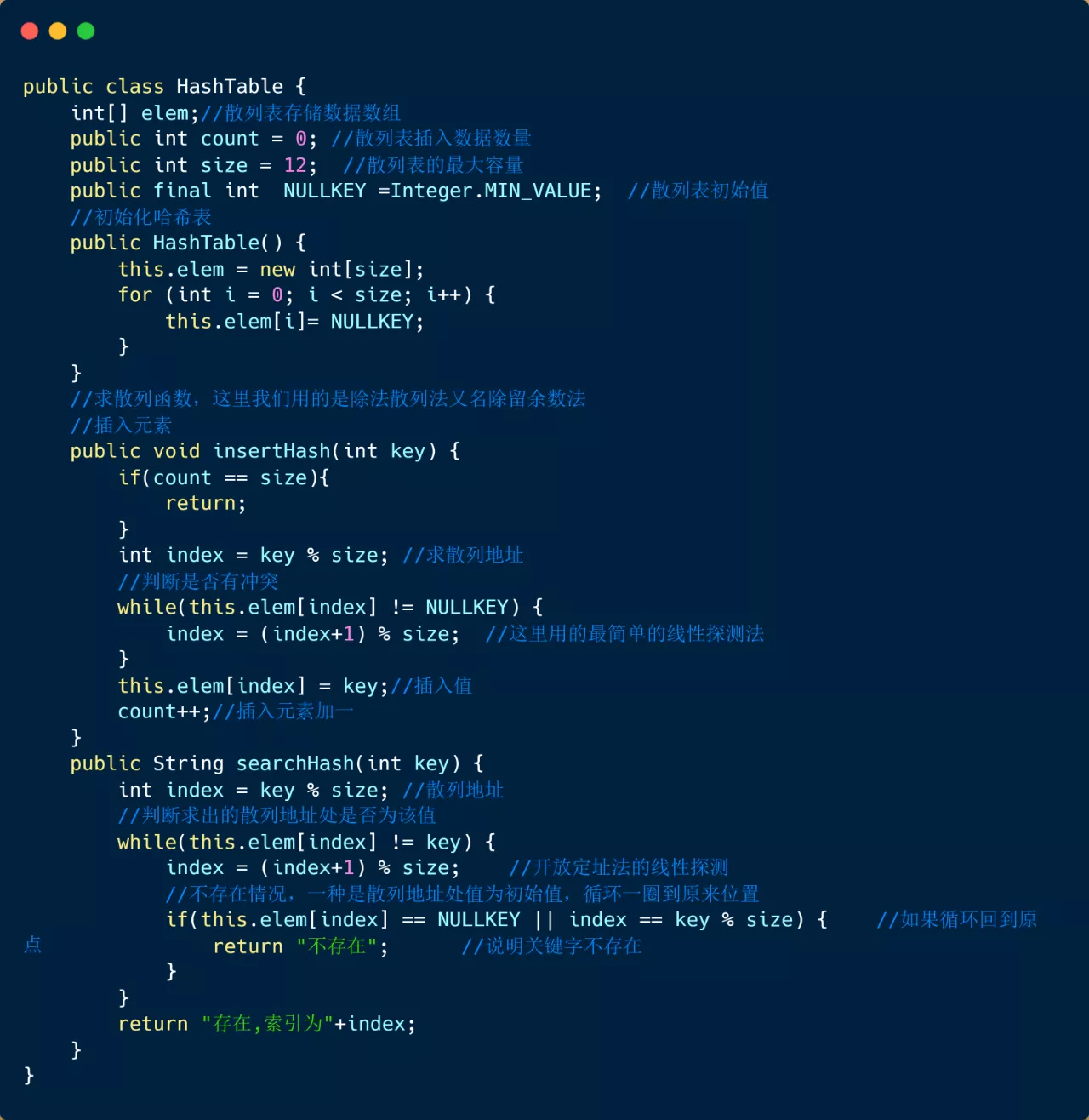
|
|
||||||
|
|
||||||
### 散列表性能分析
|
|
||||||
|
|
||||||
如果没有冲突的话,散列查找是我们查找中效率最高的,时间复杂度为O(1),但是没有冲突的情况是一种理想情况,那么散列查找的平均查找长度取决于哪些方面呢?
|
|
||||||
|
|
||||||
**1.散列函数是否均匀**
|
|
||||||
|
|
||||||
我们在上文说到,可以通过设计散列函数减少冲突,但是由于不同的散列函数对一组关键字产生冲突可能性是相同的,因此我们可以不考虑它对平均查找长度的影响。
|
|
||||||
|
|
||||||
**2.处理冲突的方法**
|
|
||||||
|
|
||||||
相同关键字,相同散列函数,不同处理冲突方式,会使平均查找长度不同,比如我们线性探测有时会堆积,则不如二次探测法好,因为链地址法处理冲突时不会产生任何堆积,因而具有最佳的平均查找性能
|
|
||||||
|
|
||||||
**3.散列表的装填因子**
|
|
||||||
|
|
||||||
本来想在上文中提到装填因子的,但是后来发现即使没有说明也不影响我们对哈希表的理解,下面我们来看一下装填因子的总结
|
|
||||||
|
|
||||||
> 装填因子 α = 填入表中的记录数 / 散列表长度
|
|
||||||
|
|
||||||
散列因子则代表着散列表的装满程度,表中记录越多,α就越大,产生冲突的概率就越大。我们上面提到的例子中 表的长度为12,填入记录数为6,那么此时的 α = 6 / 12 = 0.5 所以说当我们的 α 比较大时再填入元素那么产生冲突的可能性就非常大了。所以说散列表的平均查找长度取决于装填因子,而不是取决于记录数。所以说我们需要做的就是选择一个合适的装填因子以便将平均查找长度限定在一个范围之内。
|
|
||||||
|
|
||||||
> 各位如果能感觉到这个文章写的很用心的话,能给您带来一丢丢帮助的话,能麻烦您给这个文章点个赞吗?这样我就巨有动力写下去啦。
|
|
||||||
|
|
||||||
> 另外大家如果需要其他精选算法题的动图解析,大家可以微信关注下 【袁厨的算法小屋】,我是袁厨一个酷爱做饭所以自己考取了厨师证的菜鸡程序员,会一直用心写下去的,感谢支持!
|
|
||||||
@ -1,123 +0,0 @@
|
|||||||
## KMP算法(Knuth-Morris-Pratt)
|
|
||||||
|
|
||||||
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
|
|
||||||
|
|
||||||
我们先来看一个实例
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
|
|
||||||
|
|
||||||
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
|
|
||||||
|
|
||||||
在上面的例子中我们提到了一个名词,**最长公共前后缀**,这个是什么意思呢?下面我们通过一个较简单的例子进行描述。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
此时我们在红色阴影处匹配失败,绿色为匹配成功部分,则我们观察匹配成功的部分。
|
|
||||||
|
|
||||||
我们来看一下匹配成功部分的所有前缀
|
|
||||||
|
|
||||||
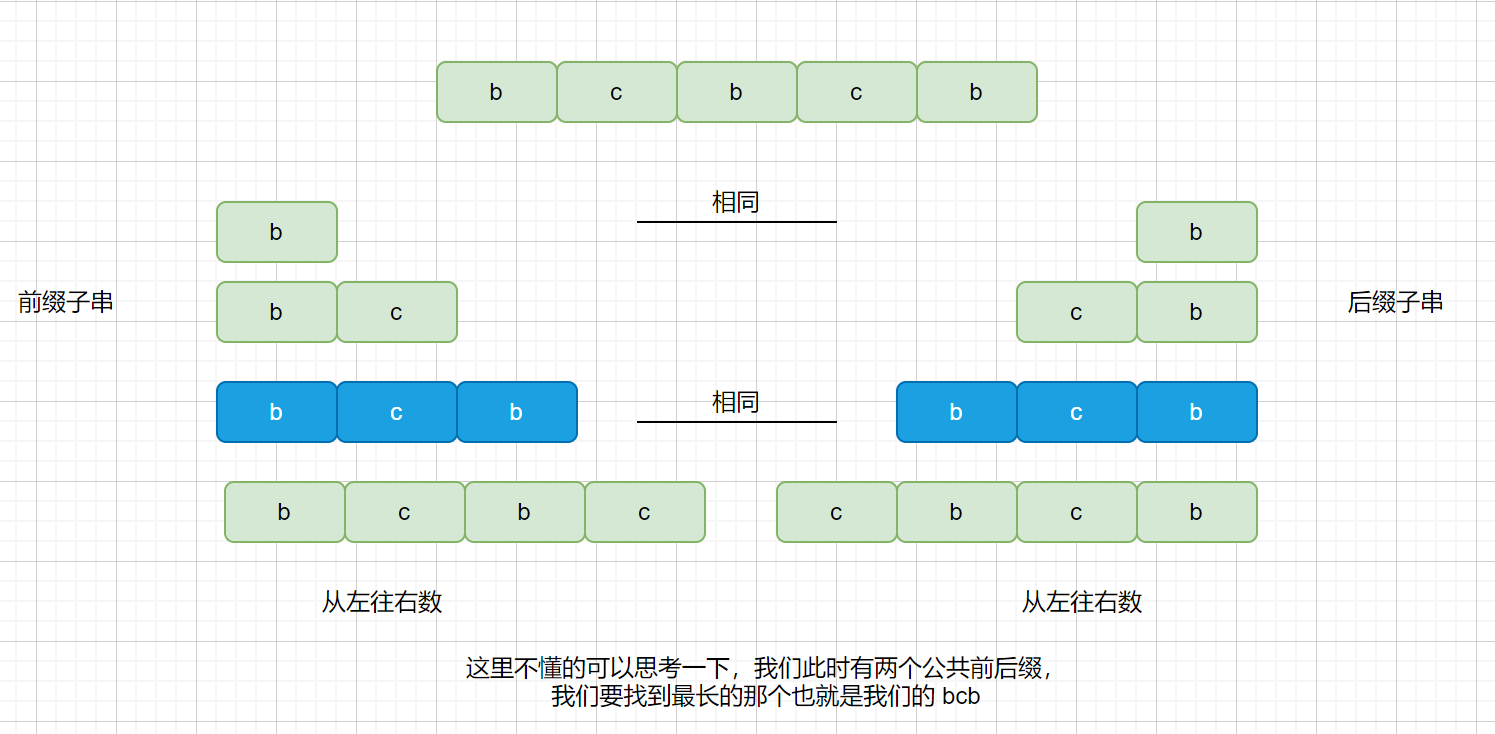
|
|
||||||
|
|
||||||
我们的最长公共前后缀如下图,则我们需要这样移动
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
|
||||||
|
|
||||||
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
|
|
||||||
|
|
||||||
next 数组存的咱们最长公共前后缀中,前缀的结尾字符下标。是不是感觉有点别扭,我们通过一个例子进行说明。
|
|
||||||
|
|
||||||
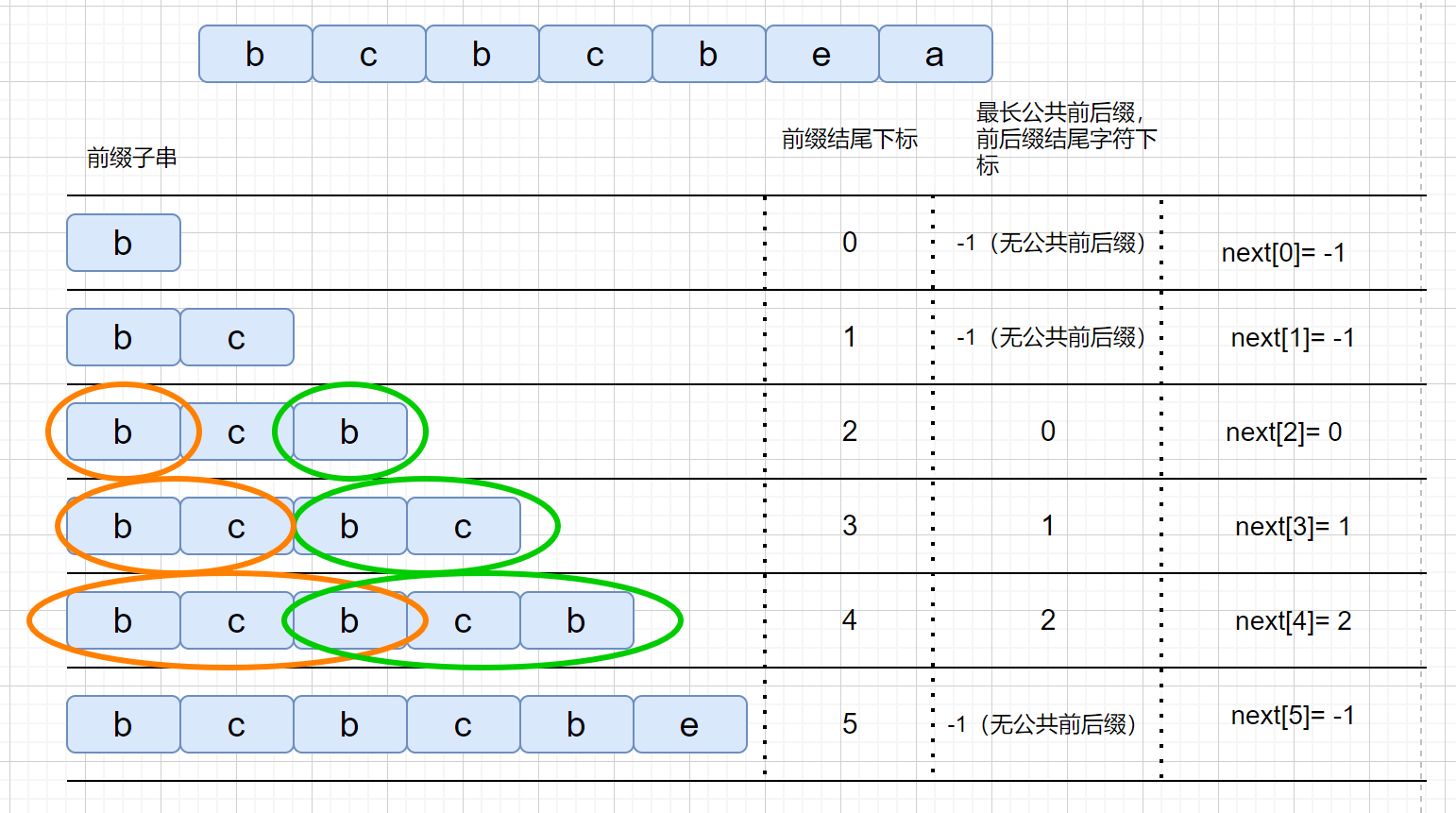
|
|
||||||
|
|
||||||
我们知道 next 数组之后,我们的 KMP 算法实现起来就很容易啦,另外我们看一下 next 数组到底是干什么用的。
|
|
||||||
|
|
||||||
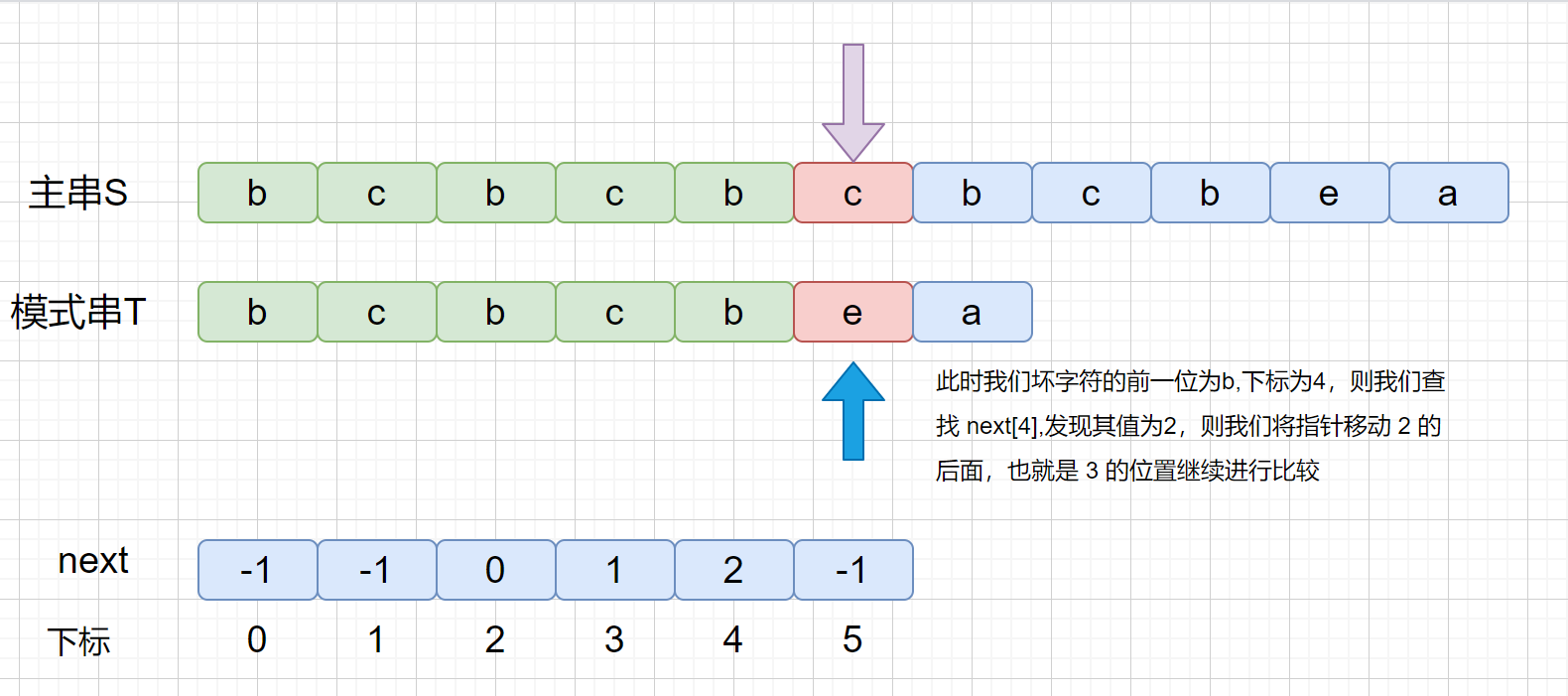
|
|
||||||
|
|
||||||
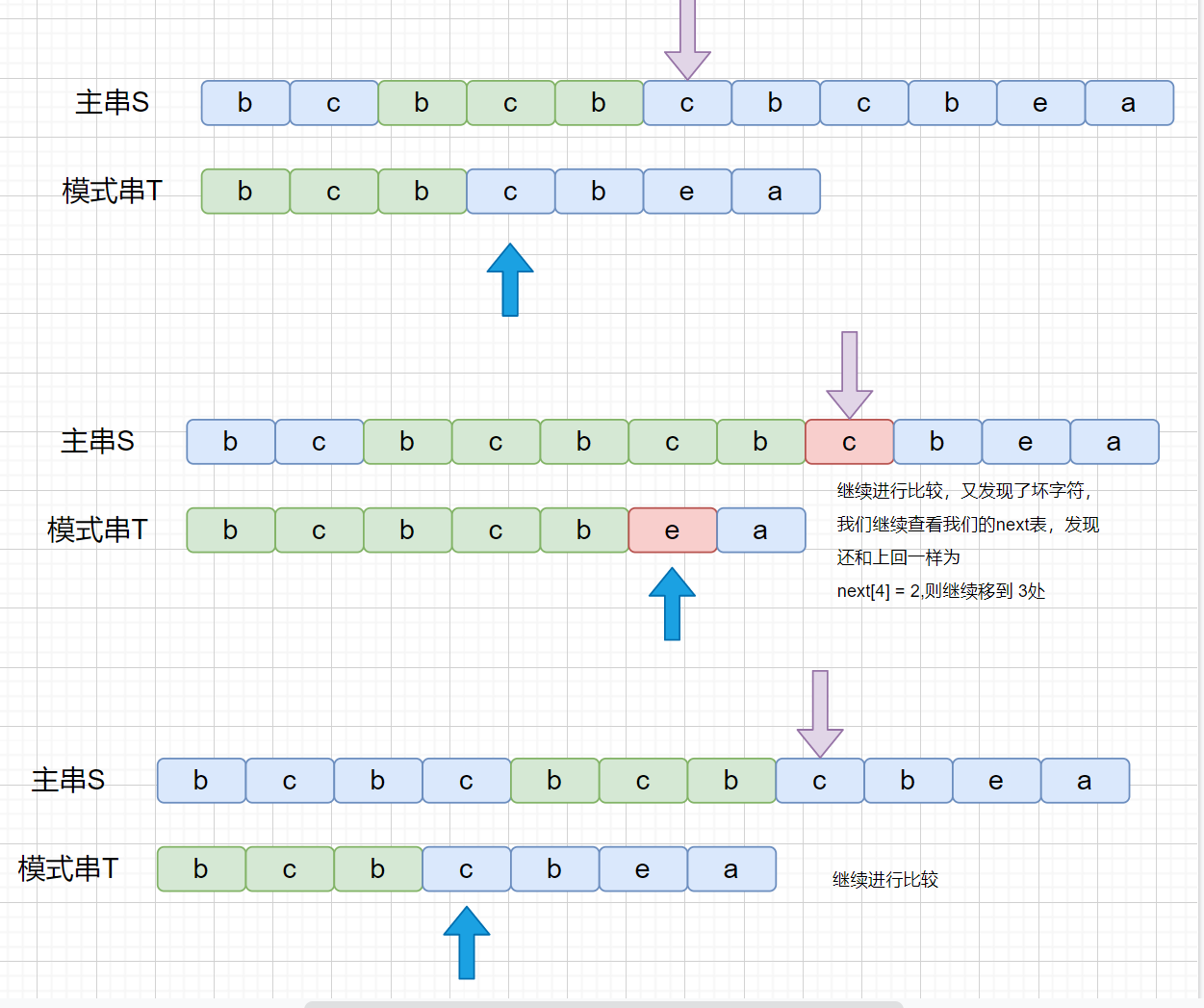
|
|
||||||
|
|
||||||
剩下的就不用说啦,完全一致啦,咱们将上面这个例子,翻译成和咱们开头对应的动画大家看一下。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
下面我们看一下代码,标有详细注释,大家认真看呀。
|
|
||||||
|
|
||||||
**注:很多教科书的 next 数组表示方式不一致,理解即可**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
//两种特殊情况
|
|
||||||
if (needle.length() == 0) {
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
if (haystack.length() == 0) {
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
// char 数组
|
|
||||||
char[] hasyarr = haystack.toCharArray();
|
|
||||||
char[] nearr = needle.toCharArray();
|
|
||||||
//长度
|
|
||||||
int halen = hasyarr.length;
|
|
||||||
int nelen = nearr.length;
|
|
||||||
//返回下标
|
|
||||||
return kmp(hasyarr,halen,nearr,nelen);
|
|
||||||
|
|
||||||
}
|
|
||||||
public int kmp (char[] hasyarr, int halen, char[] nearr, int nelen) {
|
|
||||||
//获取next 数组
|
|
||||||
int[] next = next(nearr,nelen);
|
|
||||||
int j = 0;
|
|
||||||
for (int i = 0; i < halen; ++i) {
|
|
||||||
//发现不匹配的字符,然后根据 next 数组移动指针,移动到最大公共前后缀的,
|
|
||||||
//前缀的后一位,和咱们移动模式串的含义相同
|
|
||||||
while (j > 0 && hasyarr[i] != nearr[j]) {
|
|
||||||
j = next[j - 1] + 1;
|
|
||||||
//超出长度时,可以直接返回不存在
|
|
||||||
if (nelen - j + i > halen) {
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//如果相同就将指针同时后移一下,比较下个字符
|
|
||||||
if (hasyarr[i] == nearr[j]) {
|
|
||||||
++j;
|
|
||||||
}
|
|
||||||
//遍历完整个模式串,返回模式串的起点下标
|
|
||||||
if (j == nelen) {
|
|
||||||
return i - nelen + 1;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
//这一块比较难懂,不想看的同学可以忽略,了解大致含义即可,或者自己调试一下,看看运行情况
|
|
||||||
//我会每一步都写上注释
|
|
||||||
public int[] next (char[] needle,int len) {
|
|
||||||
//定义 next 数组
|
|
||||||
int[] next = new int[len];
|
|
||||||
// 初始化
|
|
||||||
next[0] = -1;
|
|
||||||
int k = -1;
|
|
||||||
for (int i = 1; i < len; ++i) {
|
|
||||||
//我们此时知道了 [0,i-1]的最长前后缀,但是k+1的指向的值和i不相同时,我们则需要回溯
|
|
||||||
//因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标(即长度)
|
|
||||||
//就要找 k+1前一个元素在next数组里的值,即next[k+1]
|
|
||||||
while (k != -1 && needle[k + 1] != needle[i]) {
|
|
||||||
k = next[k];
|
|
||||||
}
|
|
||||||
// 相同情况,就是 k的下一位,和 i 相同时,此时我们已经知道 [0,i-1]的最长前后缀
|
|
||||||
//然后 k - 1 又和 i 相同,最长前后缀加1,即可
|
|
||||||
if (needle[k+1] == needle[i]) {
|
|
||||||
++k;
|
|
||||||
}
|
|
||||||
next[i] = k;
|
|
||||||
|
|
||||||
}
|
|
||||||
return next;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
@ -1,156 +0,0 @@
|
|||||||
# 希望这篇文章能合你的胃口
|
|
||||||
|
|
||||||
大家在学习数据结构的时候应该都学习过栈和队列,对他俩的原理应该很熟悉了,栈是先进后出,队列是后进后出。下面我们通过这篇文章来帮助小伙伴们回忆一下栈和队列的那些事。
|
|
||||||
|
|
||||||
阅读完这篇文章你会有以下收获。
|
|
||||||
|
|
||||||
了解栈和队列的意义
|
|
||||||
|
|
||||||
了解栈和队列的实现方式
|
|
||||||
|
|
||||||
了解循环队列
|
|
||||||
|
|
||||||
学会中缀表达式转后缀表达式
|
|
||||||
|
|
||||||
学会后缀表达式的运算
|
|
||||||
|
|
||||||
## 这是栈
|
|
||||||
|
|
||||||
### 栈模型
|
|
||||||
|
|
||||||
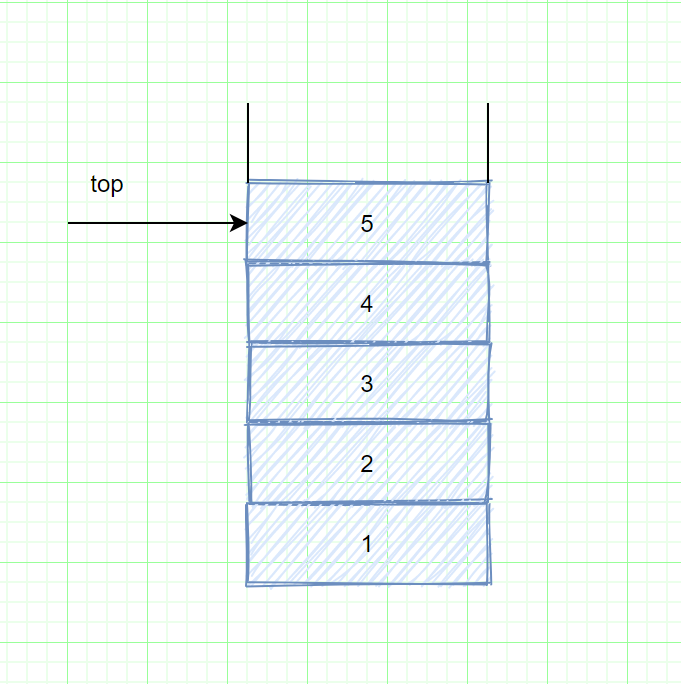
**栈(stack)是限制插入和删除只能在一个位置上进行的表**,该位置是表的末端叫做栈的顶(top),对栈的基本操作有push(进栈)和pop(出栈),前者相当于插入,后者则是删除最后插入的元素。
|
|
||||||
|
|
||||||
栈的另一个名字是LIFO(先进后出)表。普通的清空栈的操作和判断是否空栈的测试都是栈的操作指令系统的一部分,我们对栈能做的基本上也就是push和pop操作。
|
|
||||||
|
|
||||||
注:该图描述的模型只象征着push是输入操作,pop和top是输出操作
|
|
||||||
|
|
||||||
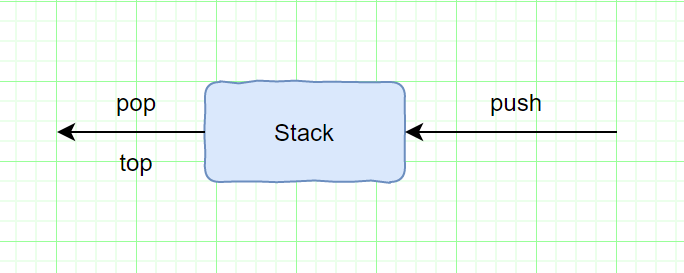
|
|
||||||
|
|
||||||
下图表示进行若干操作后的一个抽象的栈。一般的模型是,存在某个元素位于栈顶,而该元素是唯一可见元素。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 栈的实现
|
|
||||||
|
|
||||||
因为栈是一个表,因此能够实现表的方法都可以实现栈,ArrayList和LinkedList都可以支持栈操作。
|
|
||||||
|
|
||||||
刷题时我们可以直接使用Stack类来进行创建一个栈。刷题时我们可以通过下列代码创建一个栈。下面两种方式哪种都可以使用。
|
|
||||||
|
|
||||||
```
|
|
||||||
Deque<TreeNode> stack = new LinkedList<TreeNode>();//类型为TreeNode
|
|
||||||
Stack<TreeNode> stack = new Stack<TreeNode>();
|
|
||||||
```
|
|
||||||
|
|
||||||
### 栈的应用
|
|
||||||
|
|
||||||
栈在现实中应用场景很多,大家在刷题时就可以注意到,很多题目都可以用栈来解决的。下面我们来说一个比较常用的情景,数字表达式的求值。
|
|
||||||
|
|
||||||
不知道大家是否还记得那句口令,先乘除,后加减,从左算到右,有括号的话就先算括号里面的。这是我们做小学数学所用到的。四则运算中括号也是其中的一部分,先乘除后加减使运算变的复杂,加上括号后甚之,那么我们有什么办法可以让其变的更好处理呢?波兰数学家**Jan Łukasiewicz**想到了一种不需要括号的后缀表达式,,我们也将它称之为逆波兰表示。不用数学家名字命名的原因有些尴尬,居然是因为他的名字太复杂了,所以用了国籍来表示而不是姓名。所以各位小伙伴以后给孩子起名字的时候不要太复杂啊。
|
|
||||||
|
|
||||||
> 扬·武卡谢维奇([波兰语](https://baike.baidu.com/item/波兰语):*Jan Łukasiewicz*,1878年12月21日[乌克兰](https://baike.baidu.com/item/乌克兰)利沃夫 - 1956年2月13日爱尔兰都柏林),[波兰](https://baike.baidu.com/item/波兰)数学家,主要致力于[数理逻辑](https://baike.baidu.com/item/数理逻辑)的研究。著名的波兰表示法逆波兰表示法就是他的研究成果。
|
|
||||||
|
|
||||||
#### 中缀表达式转为后缀表达式
|
|
||||||
|
|
||||||
我们通过一个例子,来说明如何将中缀表达式转为后缀表达式。
|
|
||||||
|
|
||||||
例
|
|
||||||
|
|
||||||
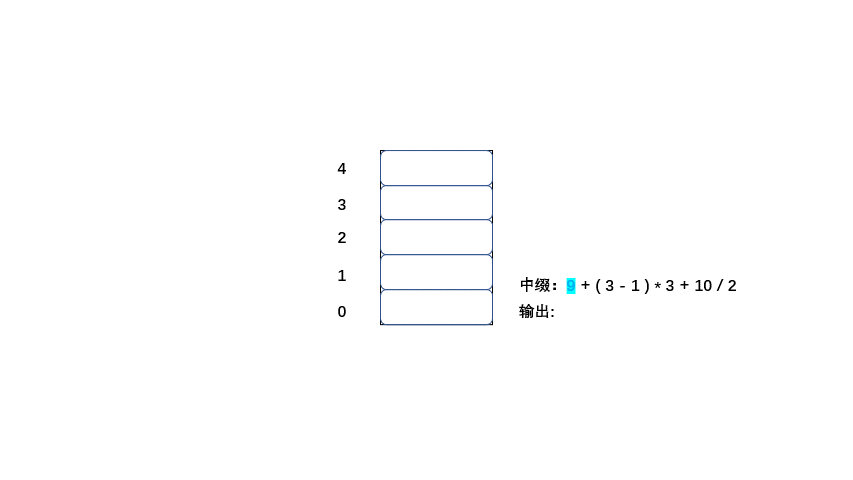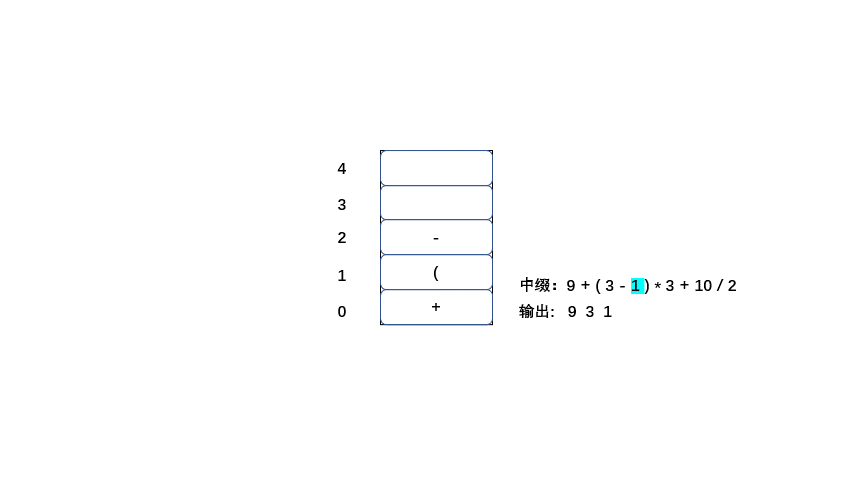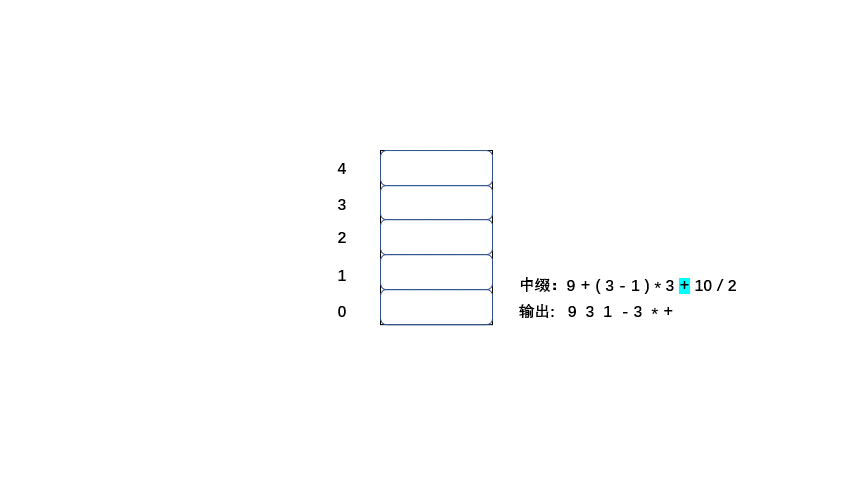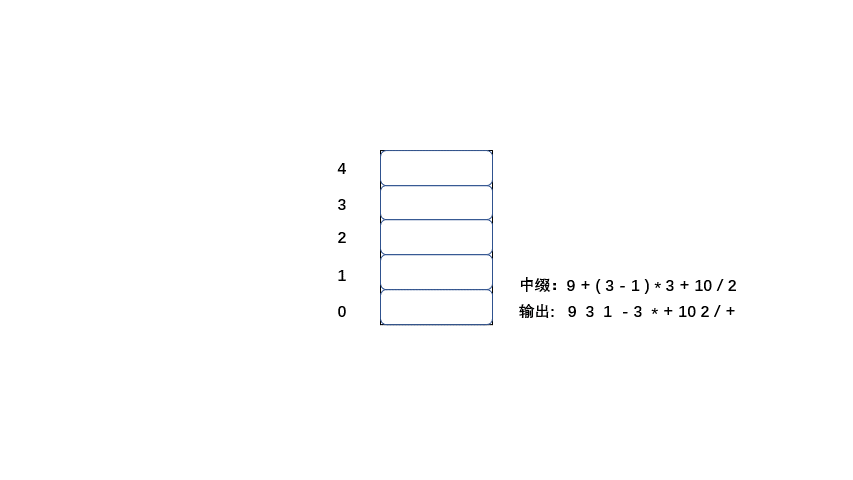
中缀:9 + ( 3 - 1 ) * 3 + 10 / 2
|
|
||||||
|
|
||||||
后缀:9 3 1 - 3 * + 10 2 / +
|
|
||||||
|
|
||||||
规则
|
|
||||||
|
|
||||||
1.从左到右遍历中缀表达式的每个数字和符号,若是数字就输出(直接成为后缀表达式的一部分,不进入栈)
|
|
||||||
|
|
||||||
2.若是符合则判断其与栈顶符号的优先级,是右括号或低于栈顶元素,则栈顶元素依次出栈并输出,等出栈完毕,当前元素入栈。
|
|
||||||
|
|
||||||
3.遵循以上两条直到输出后缀表达式为止。
|
|
||||||
|
|
||||||
老样子大家直接看动图吧简单粗暴,清晰易懂
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
#### 后缀表达式计算结果
|
|
||||||
|
|
||||||
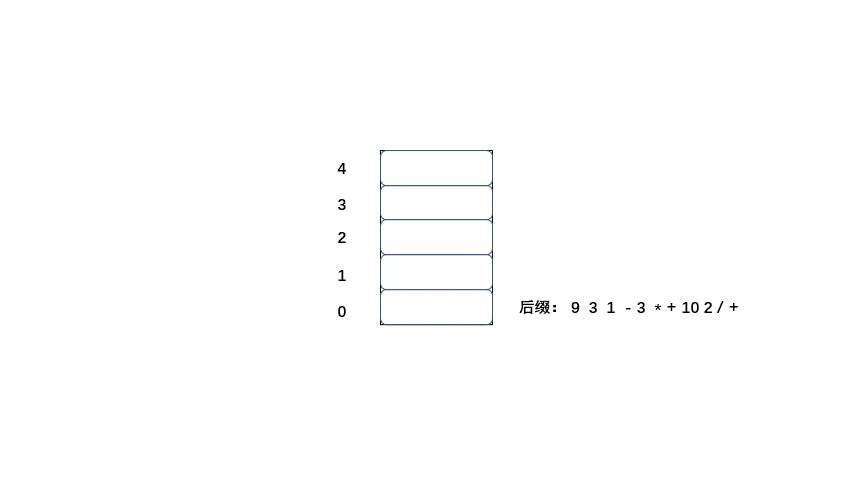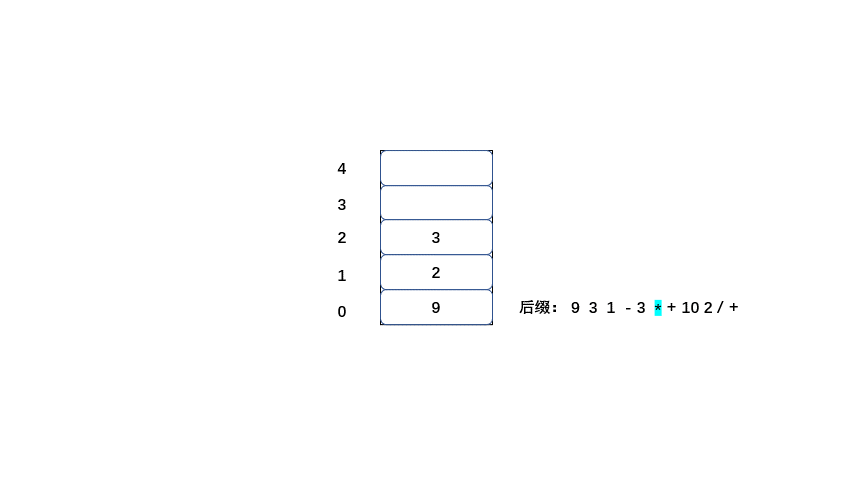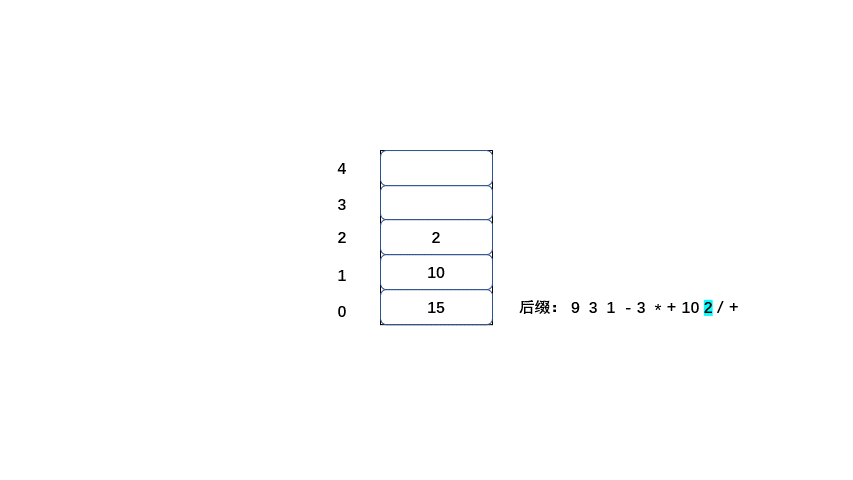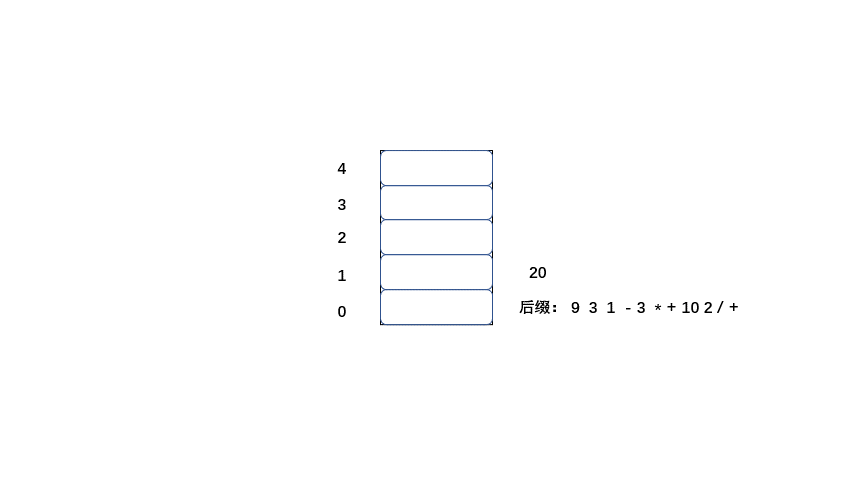
中缀:9 + ( 3 - 1 ) * 3 + 10 / 2=20
|
|
||||||
|
|
||||||
后缀:9 3 1 - 3 * + 10 2 / +
|
|
||||||
|
|
||||||
后缀表达式的值也为20,那么我们来了解一下计算机是如何将后缀表达式计算为20的。
|
|
||||||
|
|
||||||
规则:
|
|
||||||
|
|
||||||
1.从左到右遍历表达式的每个数字和符号,如果是数字就进栈
|
|
||||||
|
|
||||||
2.如果是符号就将栈顶的两个数字出栈,进行运算,并将结果入栈,一直到获得最终结果。
|
|
||||||
|
|
||||||
下面大家 继续看动图吧。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
注:为了用动图把逻辑整的清晰明了,十几秒的动图,就要整半个多小时,改进好几遍。如果觉得图片对你有帮助的话就点个赞和在看吧。
|
|
||||||
|
|
||||||
## 这是队列
|
|
||||||
|
|
||||||
### 队列模型
|
|
||||||
|
|
||||||
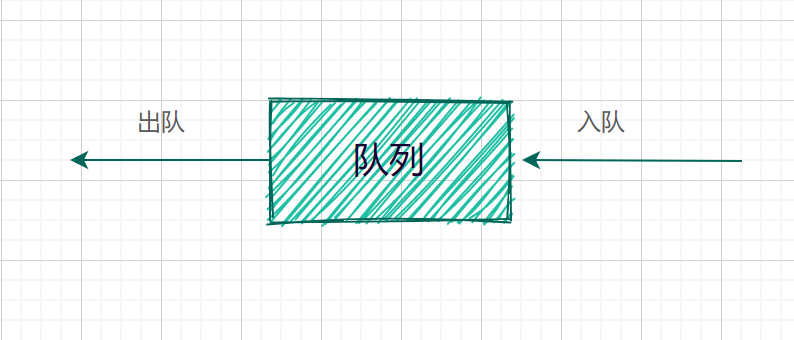
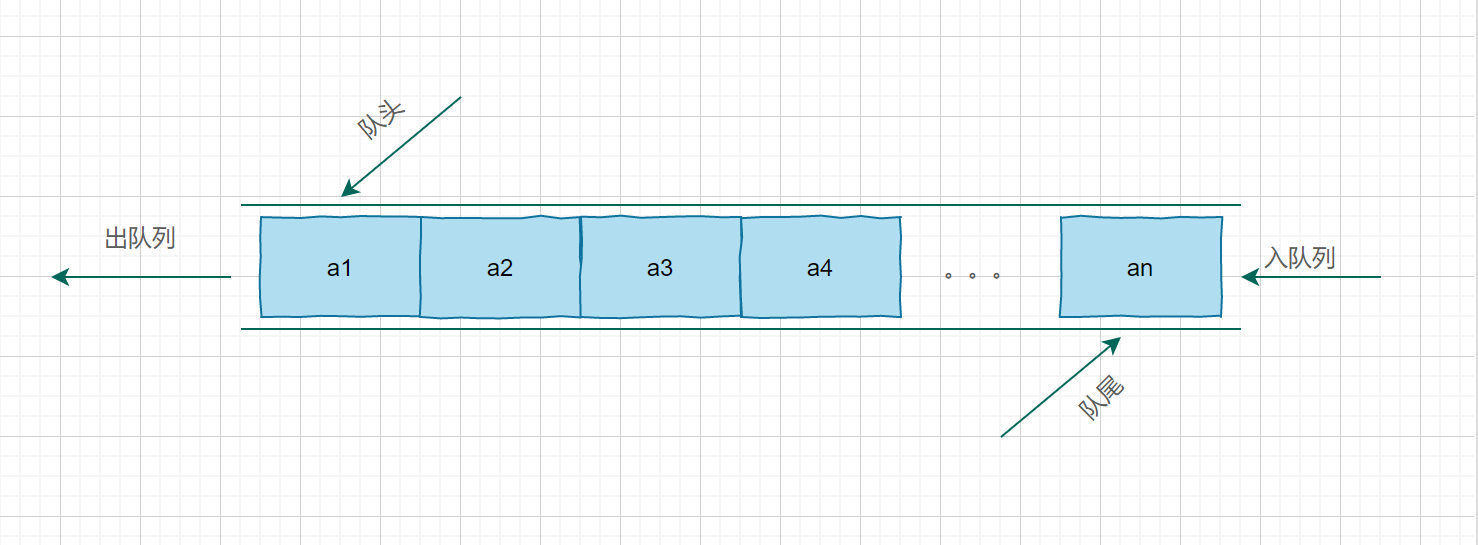
像栈一样,队列(queue)也是表。然而使用队列时插入在一端进行而删除在另一端进行,遵守先进先出的规则。所以队列的另一个名字是(FIFO)。
|
|
||||||
|
|
||||||
队列的基本操作是入队(enqueue):它是在表的末端(队尾(rear)插入一个元素。出队(dequeue):出队他是删除在表的开头(队头(front))的元素。
|
|
||||||
|
|
||||||
注:下面模型只象征着输入输出操作
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
具体模型
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 队列的实现
|
|
||||||
|
|
||||||
队列我们在树的层次遍历时经常使用,后面我们写到树的时候会给大家整理框架。队列同样也可以由数组和LinkedList实现,刷题时比较常用的方法是
|
|
||||||
|
|
||||||
```
|
|
||||||
Queue<TreeNode> queue = new LinkedList<TreeNode>();
|
|
||||||
```
|
|
||||||
|
|
||||||
### 循环队列
|
|
||||||
|
|
||||||
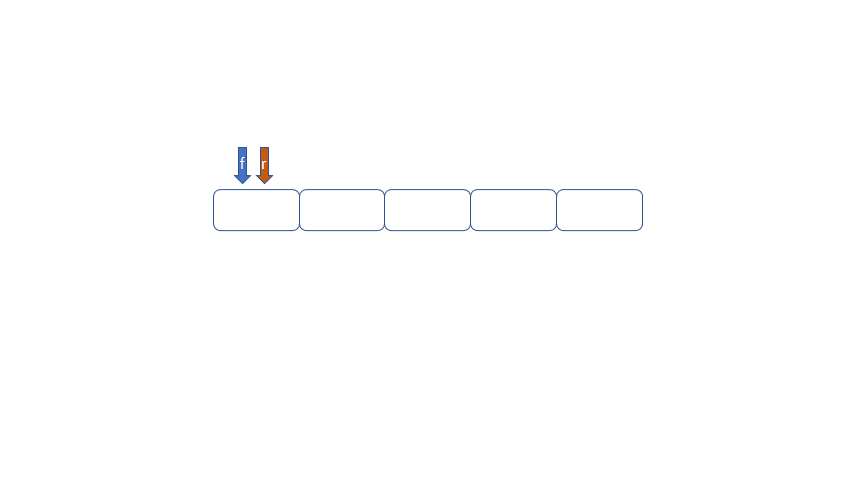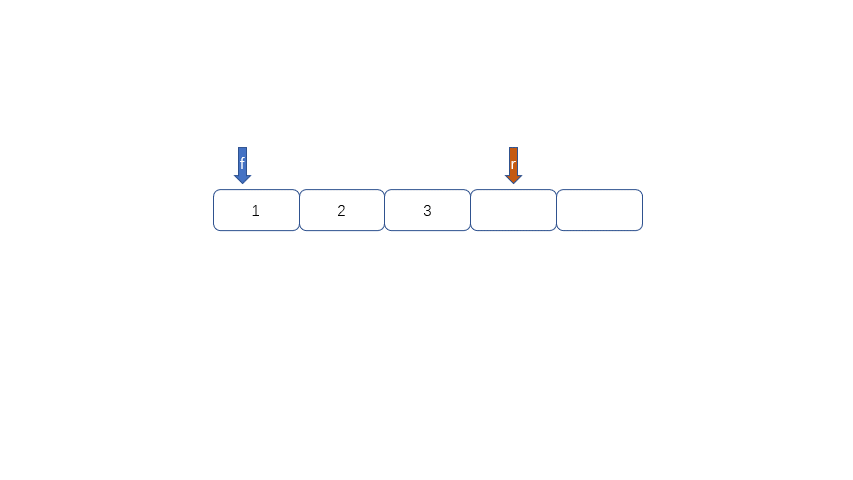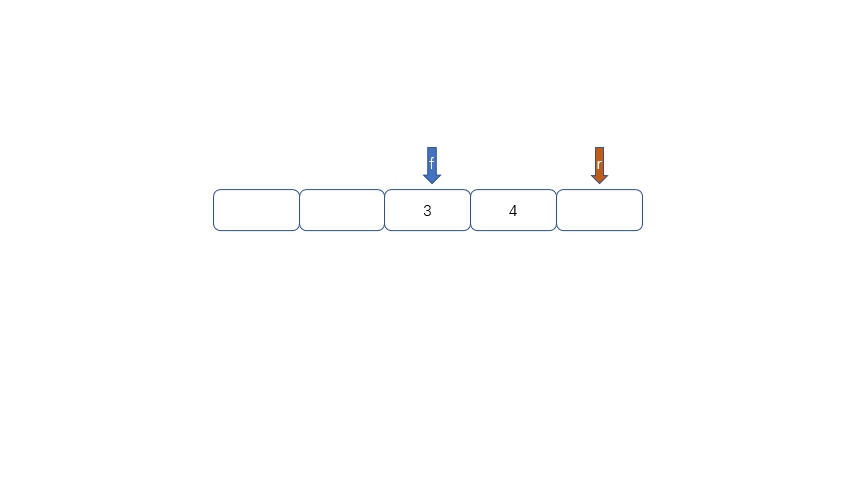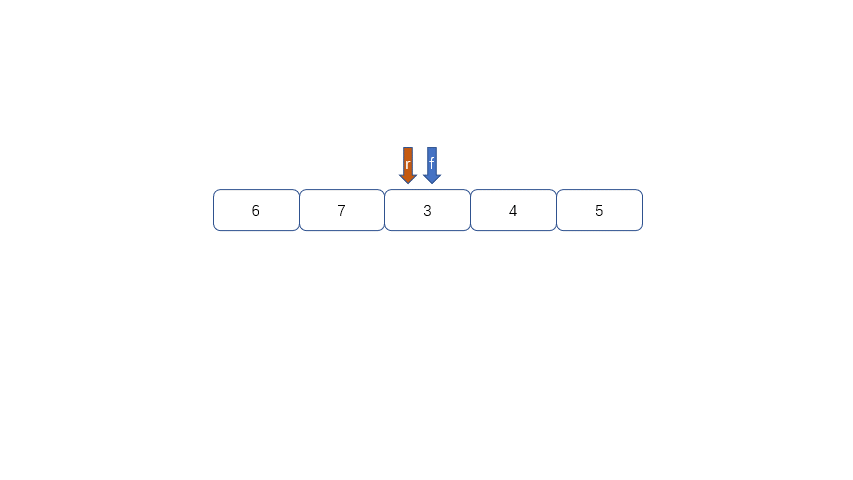
循环队列的出现就是为了解决队列的假溢出问题。何为假溢出呢?我们运用数组实现队列时,数组长度为5,我们放入了[1,2,3,4,5],我们将1,2出队,此时如果继续加入6时,因为数组末尾元素已经被占用,再向后加则会溢出,但是我们的下标0,和下标1还是空闲的。所以我们把这种现象叫做“假溢出”。
|
|
||||||
|
|
||||||
例如,我们在学校里面排队洗澡一人一个格,当你来到澡堂发现前面还有两个格,但是后面已经满了,你是去前面洗,还是等后面格子的哥们洗完再洗?肯定是去前面的格子洗。除非澡堂的所有格子都满了。我们才会等。
|
|
||||||
|
|
||||||
所以我们用来解决假溢出的方法就是后面满了,就再从头开始,也就是头尾相接的循环,我们把队列的这种头尾相接的顺序存储结构成为循环队列。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们发现队列为空时front == rear,队列满时也是front == rear,那么问题来了,我们应该怎么区分满和空呢?
|
|
||||||
|
|
||||||
我们可以通过以下两种方法进行区分,
|
|
||||||
|
|
||||||
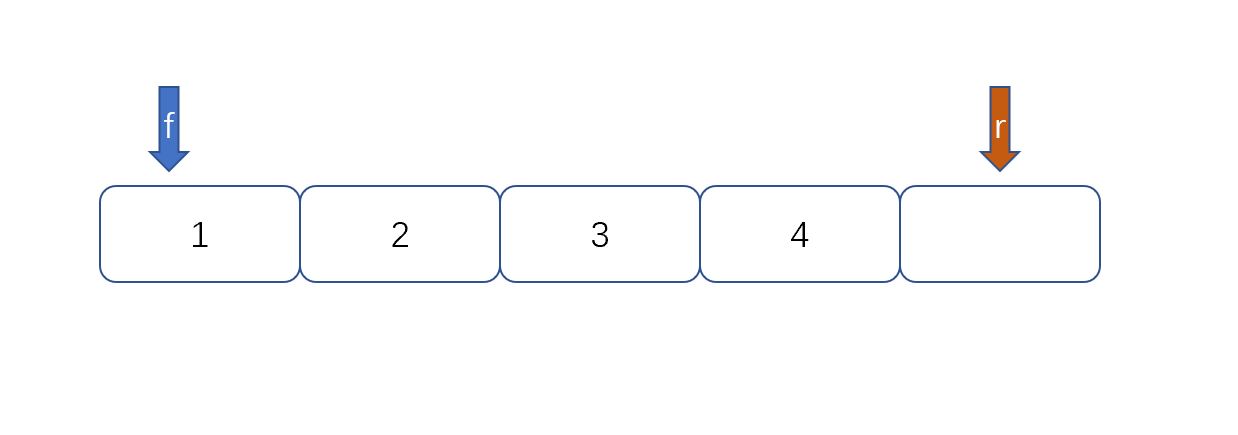
1.设置标记变量flag;当front==rear 时且flag==0时为空,当front==rear且rear为1时且flag==1时为满
|
|
||||||
|
|
||||||
2.当队列为空时,front==rear,当队列满是我们保留一个元素空间,也就是说,队列满时,数组内还有一个空间。
|
|
||||||
|
|
||||||
例:
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
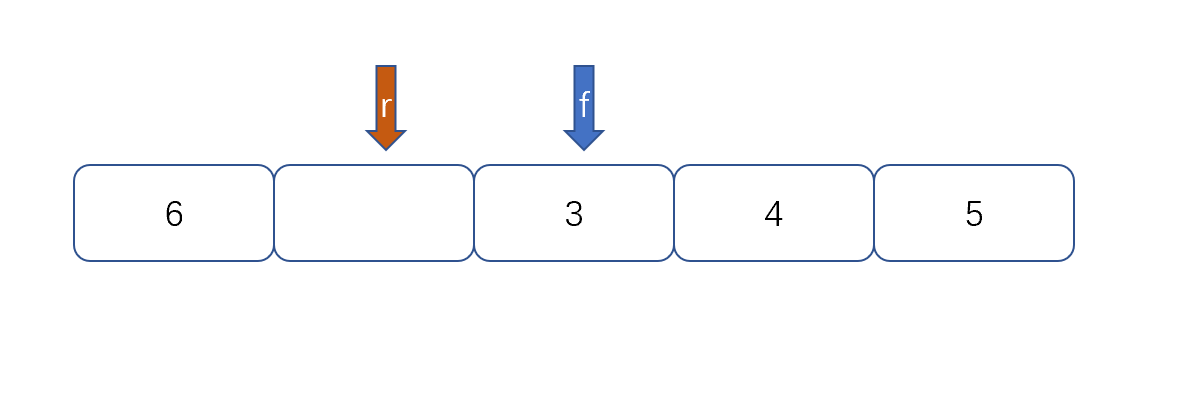
|
|
||||||
|
|
||||||
然后我们再根据以下公式则能够判断队列满没满了。
|
|
||||||
|
|
||||||
(rear+1)%queuesize==front
|
|
||||||
|
|
||||||
queuesize,代表队列的长度,上图为5。我们来判断上面两张图是否满。(4+1)%5==0,(2+1)%5==3
|
|
||||||
|
|
||||||
两种情况都是满的,over。
|
|
||||||
|
|
||||||
注:为了用动图把逻辑整的清晰明了,十几秒的动图,就要整半个多小时,改进好几遍。如果觉得图片对你有帮助的话就点个赞和在看吧。
|
|
||||||
@ -1,151 +0,0 @@
|
|||||||
# 链表详解
|
|
||||||
|
|
||||||
阅读完本文你会有以下收获
|
|
||||||
|
|
||||||
1.知道什么是链表?
|
|
||||||
|
|
||||||
2.了解链表的几种类型。
|
|
||||||
|
|
||||||
3.了解链表如何构造。
|
|
||||||
|
|
||||||
4.链表的存储方式
|
|
||||||
|
|
||||||
5.如何遍历链表
|
|
||||||
|
|
||||||
6.了解链表的操作。
|
|
||||||
|
|
||||||
7.知道链表和数组的不同点
|
|
||||||
|
|
||||||
8.掌握链表的经典题目。
|
|
||||||
|
|
||||||
### 链表的定义:
|
|
||||||
|
|
||||||
> 定义:链表是一种递归的数据结构,他或者为空(null),或者是指向一个结点(node)的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。
|
|
||||||
|
|
||||||
我们来对其解读一下,链表是一种常见且基础的数据结构,是一种线性表,但是他不是按线性顺序存取数据,而是在每一个节点里存到下一个节点的地址。我们可以这样理解,链表是通过指针串联在一起的线性结构,每一个链表结点由两部分组成,数据域及指针域,链表的最后一个结点指向null。也就是我们所说的空指针。
|
|
||||||
|
|
||||||
### 链表的几种类型
|
|
||||||
|
|
||||||
我们先来看一下链表的可视化表示方法,以便更好的对其理解。
|
|
||||||
|
|
||||||
- 用长方形表示对象
|
|
||||||
- 将实例变量的值写在长方形中;
|
|
||||||
- 用指向被引用对象的箭头表示引用关系。
|
|
||||||
|
|
||||||
#### 单链表
|
|
||||||
|
|
||||||
一个单向链表包含两个值: 当前节点的值和一个指向下一个节点的链接。
|
|
||||||
|
|
||||||
我们通过上面说到的可视化表示方法,构造单链表的可视化模型,如图所示。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
#### 双向链表
|
|
||||||
|
|
||||||
上面提到了单链表的节点只能指向节点的下一个节点。而双向链表有三个整数值: 数值、向后的节点链接、向前的节点链接,所以双链表既能向前查询也可以向后查询。
|
|
||||||
|
|
||||||
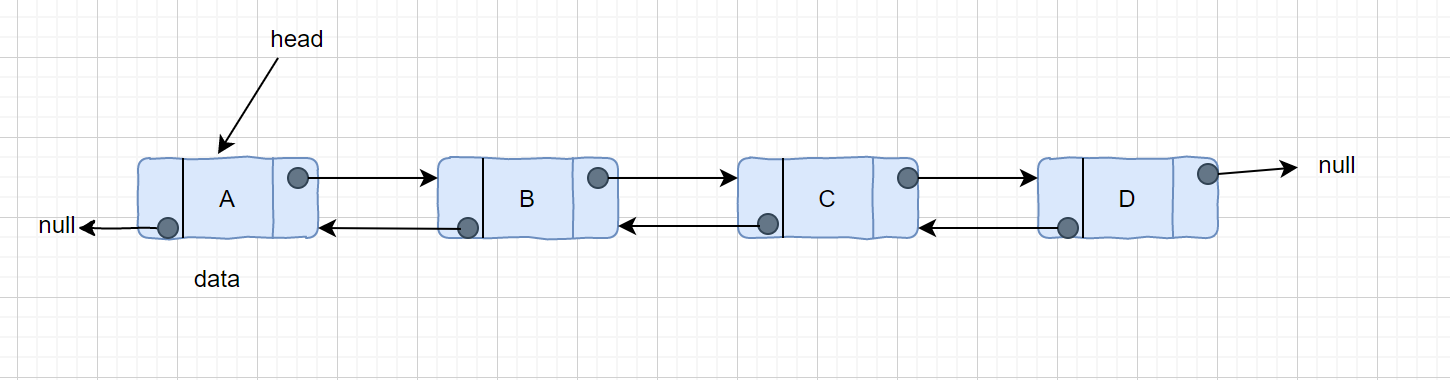
|
|
||||||
|
|
||||||
####
|
|
||||||
|
|
||||||
还有一个常用的链表则为循环单链表,则单链表尾部的指针指向头节点。例如在leetcode61旋转链表中,我们就是先将链表闭合成环,找到新的打开位置,并定义新的表头和表尾。
|
|
||||||
|
|
||||||
### 构造链表
|
|
||||||
|
|
||||||
java是面向对象语言,实现链表很容易。我们首先用一个嵌套类来定义节点的抽象数据类型
|
|
||||||
|
|
||||||
```java
|
|
||||||
private class Node {
|
|
||||||
Item item;
|
|
||||||
Node next;
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
现在我们需要构造一条含有one,two,three的链表,我们首先为每个元素创造一个节点
|
|
||||||
|
|
||||||
```java
|
|
||||||
Node first = new Node();
|
|
||||||
Node second = new Node();
|
|
||||||
Node third = new Node();
|
|
||||||
```
|
|
||||||
|
|
||||||
将每个节点的item域设为所需的值
|
|
||||||
|
|
||||||
```java
|
|
||||||
first.item = "one";
|
|
||||||
second.item = "two";
|
|
||||||
third.item = "three";
|
|
||||||
```
|
|
||||||
|
|
||||||
然后我们设置next域来构造链表
|
|
||||||
|
|
||||||
```java
|
|
||||||
first.next = second;
|
|
||||||
second.next = third;
|
|
||||||
```
|
|
||||||
|
|
||||||
注:此时third的next仍为null,即被初始化的值。
|
|
||||||
|
|
||||||
### 链表的存储方式
|
|
||||||
|
|
||||||
我们知道了如何构造链表,我们再来说一下链表的存储方式。
|
|
||||||
|
|
||||||
我们都知道数组在内存中是连续分布的,但是链表在内存不是连续分配的。链表是通过指针域的指针链接内存中的各个节点。
|
|
||||||
|
|
||||||
所以链表在内存中是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。我们可以根据下图来进行理解。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 遍历链表
|
|
||||||
|
|
||||||
链表的遍历我们通常使用while循环(for循环也可以但是代码不够简洁)下面我们来看一下链表的遍历代码
|
|
||||||
|
|
||||||
for:
|
|
||||||
|
|
||||||
```java
|
|
||||||
for (Node x = first; x != null; x = x.next) {
|
|
||||||
//处理x.item
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
while:
|
|
||||||
|
|
||||||
```
|
|
||||||
Node x = first;
|
|
||||||
while (x!=null) {
|
|
||||||
//处理x.item
|
|
||||||
x = x.next;
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
### 链表的几种操作
|
|
||||||
|
|
||||||
#### 添加节点
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
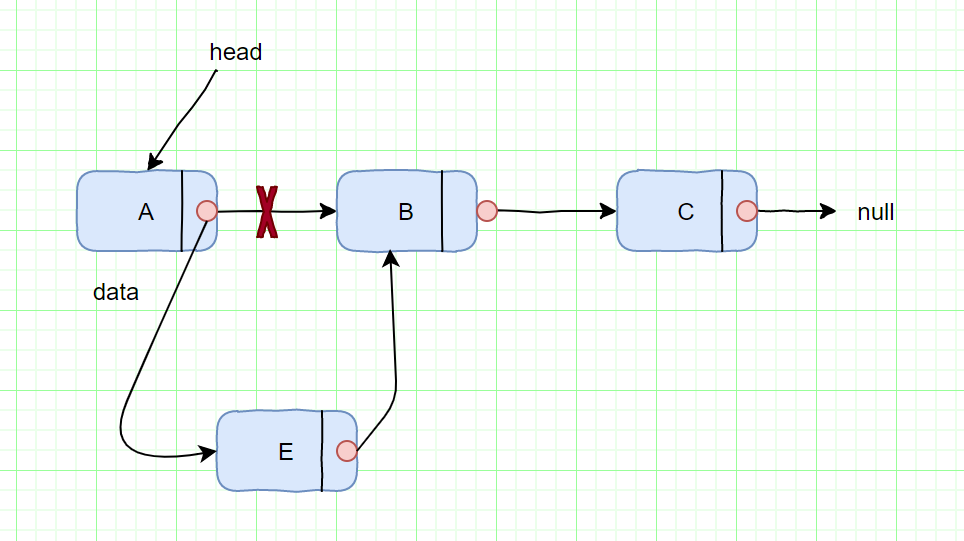
#### 删除节点
|
|
||||||
|
|
||||||
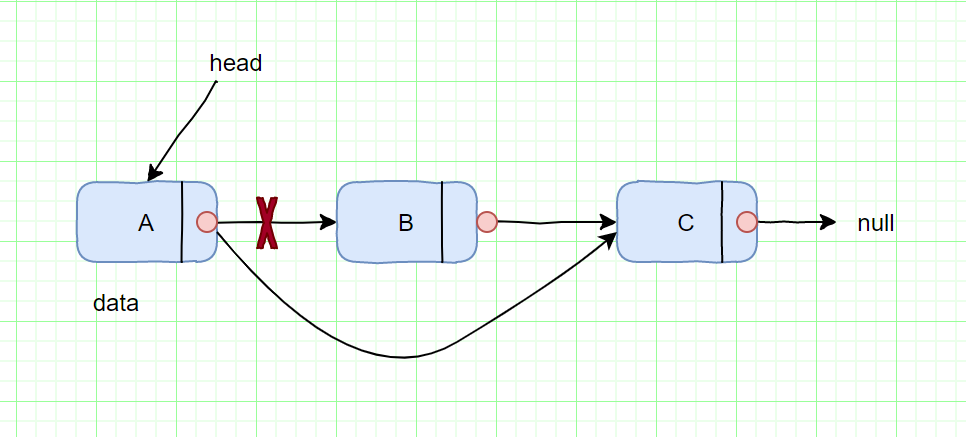
删除B节点,如图所示
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们只需将A节点的next指针指向C节点即可。
|
|
||||||
|
|
||||||
有的同学可能会有这种疑问,B节点这样不会留着内存里吗?java含有自己的内存回收机制,不用自己手动释放内存了,但是C++,则需要手动释放。
|
|
||||||
|
|
||||||
我们通过上图的删除和插入都是O(1)操作。
|
|
||||||
|
|
||||||
链表和数组的比较
|
|
||||||
|
|
||||||
| | 插入/删除操作(时间复杂度) | 查询(时间复杂度) | 存储方式 |
|
|
||||||
| ---- | ------------------------- | ------------------ | ------------ |
|
|
||||||
| 数组 | O(n) | O(1) | 内存连续分布 |
|
|
||||||
| 链表 | O(1) | O(n) | 内存散乱分布 |
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
@ -1,192 +0,0 @@
|
|||||||
**写在前面**
|
|
||||||
|
|
||||||
袁记菜馆内
|
|
||||||
|
|
||||||
> 袁厨:小二,最近快要过年了,咱们店也要给大家发点年终奖啦,你去根据咱们的**红黑豆小本本**,看一下大家都该发多少的年终奖,然后根据金额从小到大排好,按顺序一个一个发钱,大家回去过个好年,你也老大不小了,回去取个媳妇。
|
|
||||||
>
|
|
||||||
> 小二:好滴掌柜的,我现在马上就去。
|
|
||||||
|
|
||||||
上面说到的按照金额从大到小排好就是我们今天要讲的内容 --- 排序。
|
|
||||||
|
|
||||||
排序是我们生活中经常会面对的问题,体育课的时候,老师会让我们从矮到高排列,考研录取时,成绩会按总分从高到底进行排序(考研的各位读者,你们必能收到心仪学校给你们寄来的大信封),我们网购时,有时会按销量从高到低,价格从低到高,将最符合咱们预期的商品列在前面。
|
|
||||||
|
|
||||||
概念:将杂乱无章的数据元素,通过**一定的方法**(排序算法)按**关键字**(k)顺序排列的过程叫做排序。例如我们上面的销量和价格就是关键字
|
|
||||||
|
|
||||||
**排序算法的稳定性**
|
|
||||||
|
|
||||||
什么是排序算法的稳定性呢?
|
|
||||||
|
|
||||||
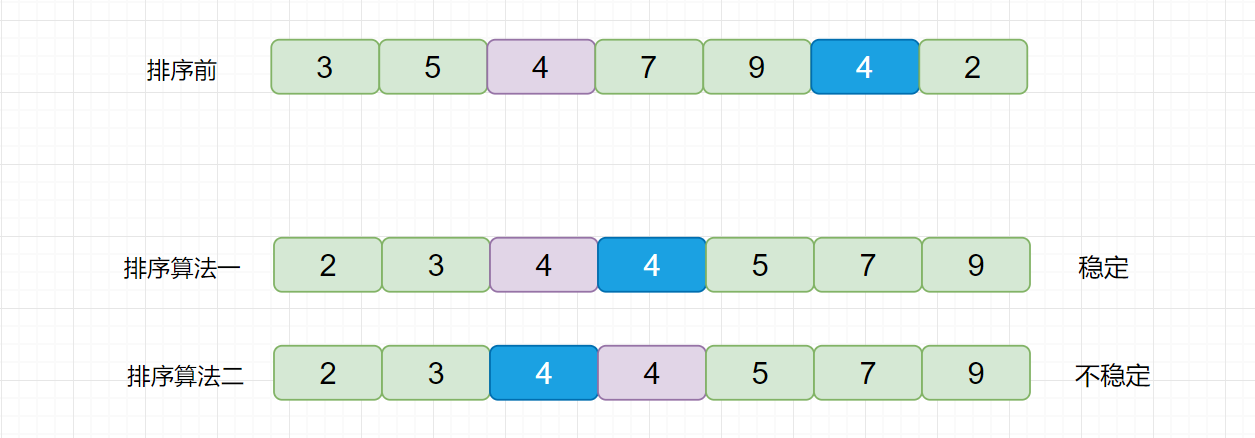
因为我们待排序的记录序列中可能存在两个或两个以上的关键字相等的记录,**排序结果可能会存在不唯一的情况**,所以我们排序之后,如果相等元素之间**原有的先后顺序不变**。则称所用的排序方法是**稳定的**,反之则称之为**不稳定的**。见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
例如上图,我们的数组中有两个相同的元素 4, 我们分别用不同的排序算法对其排序,算法一排序之后,两个相同元素的**相对位置**没有发生改变,我们则称之为**稳定的排序算法**,算法二排序之后相对位置发生改变,则为**不稳定的排序算法**。
|
|
||||||
|
|
||||||
那排序算法的稳定性又有什么用呢?
|
|
||||||
|
|
||||||
在我们做题中大多只是将数组进行排序,只需考虑时间复杂度空间复杂度等指标,排序算法是否稳定,一般不进行考虑。但是在真正软件开发中排序算法的稳定性是一个特别重要的衡量指标。继续说我们刚才的例子。我们想要实现年终奖从少到多的排序,然后相同年终奖区间内的红豆数也按照从少到多进行排序。
|
|
||||||
|
|
||||||
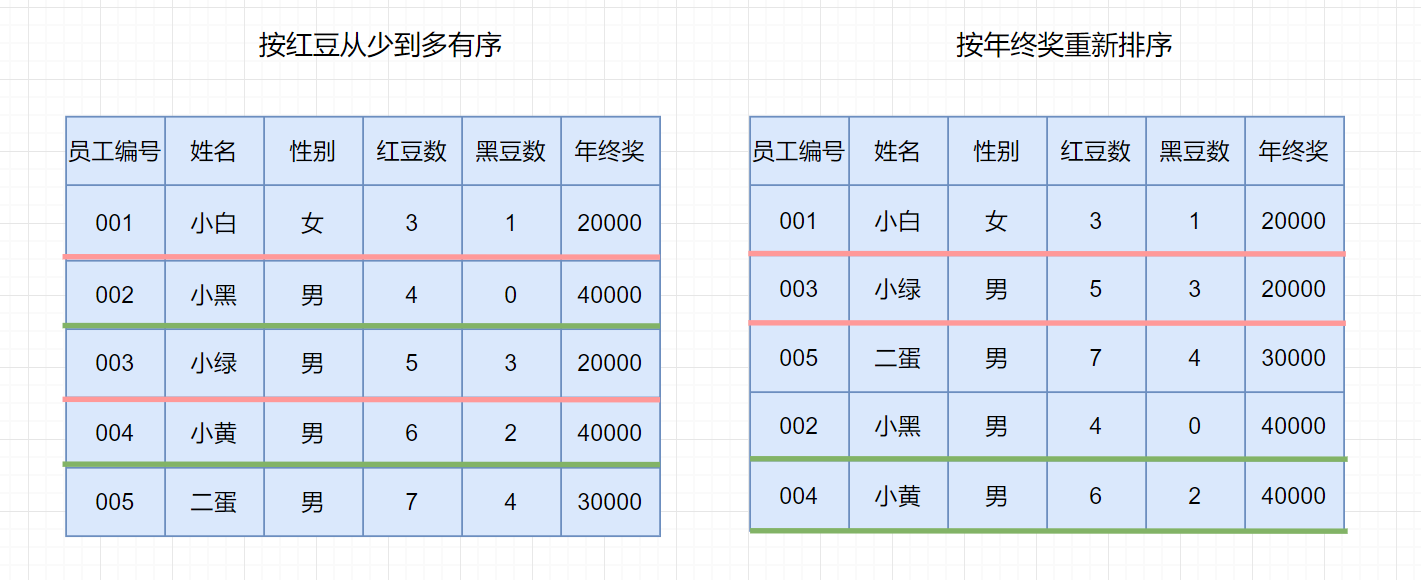
排序算法的稳定性在这里就显得至关重要。这是为什么呢?见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
第一次排序之后,所有的职工按照**红豆数**从少到多有序。
|
|
||||||
|
|
||||||
第二次排序中,我们使用**稳定的排序算法**,所以经过第二次排序之后,年终奖相同的职工,仍然保持着红豆的有序(想对位置不变),红豆仍是从小到大排序。我们使用稳定的排序算法,只需要两次排序即可。
|
|
||||||
|
|
||||||
稳定排序可以让第一个关键字排序的结果服务于第二个关键字排序中数值相等的那些数。
|
|
||||||
|
|
||||||
上述情况如果我们利用不稳定的排序算法,实现这一效果是十分复杂的。
|
|
||||||
|
|
||||||
**比较类和非比较类**
|
|
||||||
|
|
||||||
我们根据元素是否依靠与其他元素的比较来决定元素间的相对次序。以此来区分比较类排序算法和非比较类排序算法。
|
|
||||||
|
|
||||||
**内排序和外排序**
|
|
||||||
|
|
||||||
内排序是在排序的整个过程中,待排序的所有记录全部被放置在内存中。外排序是由于排序的记录个数太多,不能同时放置在内存中,整个排序过程需要在内外存之间多次交换数据才能进行,常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
|
|
||||||
|
|
||||||
对我们内排序来说,我们主要受三个方面影响,时间性能,辅助空间,算法的复杂性
|
|
||||||
|
|
||||||
**时间性能**
|
|
||||||
|
|
||||||
在我们的排序算法执行过程中,主要执行两种操作比较和交换,比较是排序算法最起码的操作,移动指记录从一个位置移动到另一个位置。所以我们一个高效的排序算法,应该尽可能少的比较和移动。
|
|
||||||
|
|
||||||
**辅助空间**
|
|
||||||
|
|
||||||
执行算法所需要的辅助空间的多少,也是来衡量排序算法性能的一个重要指标
|
|
||||||
|
|
||||||
**算法的复杂度**
|
|
||||||
|
|
||||||
这里的算法复杂度不是指算法的时间复杂度,而是指算法本身的复杂度,过于复杂的算法也会影响排序的性能。
|
|
||||||
|
|
||||||
下面我们一起复习两种**简单排序算法**,**冒泡排序**和**简单选择排序**,看看有没有之前忽略的东西。
|
|
||||||
|
|
||||||
### **冒泡排序**(Bubble Sort)
|
|
||||||
|
|
||||||
估计我们在各个算法书上介绍排序时,第一个估计都是冒泡排序。主要是这个排序算法思路最简单,也最容易理解,(也可能是它的名字好听,哈哈),学过的老哥们也一起来复习一下吧,我们一起深挖一下冒泡排序。
|
|
||||||
|
|
||||||
冒泡排序的基本思想是,**两两比较相邻记录的关键字**,如果是反序则交换,直到没有反序为止。冒泡一次冒泡会让至少一个元素移动到它应该在的位置,那么如果数组有 n 个元素,重复 n 次后则能完成排序。根据定义可知那么冒泡排序显然是一种比较类排序。
|
|
||||||
|
|
||||||
**最简单的排序实现**
|
|
||||||
|
|
||||||
我们来看一下这段代码
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
int len = nums.length;
|
|
||||||
for (int i = 0; i < len; ++i) {
|
|
||||||
for (int j = i+1; j < len; ++j) {
|
|
||||||
if (nums[i] > nums[j]) {
|
|
||||||
swap(nums,i,j);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
|
|
||||||
}
|
|
||||||
public void swap(int[] nums,int i,int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
我们来思考一下上面的代码,每次让关键字 nums[i] 和 nums[j] 进行比较如果 nums[i] > nums[j] 时则进行交换,这样 nums[0] 在经过一次循环后一定为最小值。那么这段代码是冒泡排序吗?
|
|
||||||
|
|
||||||
显然不是,我们冒泡排序的思想是两两比较**相邻记录**的关键字,注意里面有相邻记录,所以这段代码不是我们的冒泡排序,下面我们用动图来模拟一下冒泡排序的执行过程,看完之后一定可以写出正宗的冒泡排序。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
**题目代码**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
int len = nums.length;
|
|
||||||
for (int i = 0; i < len; ++i) {
|
|
||||||
for (int j = 0; j < len - i - 1; ++j) {
|
|
||||||
if (nums[j] > nums[j+1]) {
|
|
||||||
swap(nums,j,j+1);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
public void swap(int[] nums,int i,int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
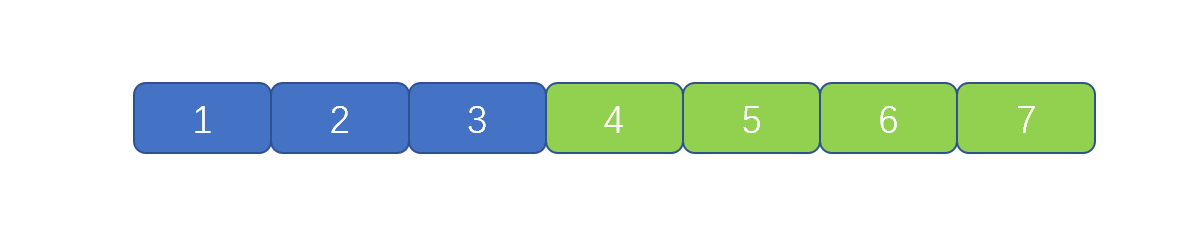
上图中的代码则为正宗的冒泡排序代码,但是我们是不是发现了这个问题
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们此时数组已经完全有序了,可以直接返回,但是动图中并没有返回,而是继续执行,那我们有什么办法让其完全有序时,直接返回,不继续执行吗?
|
|
||||||
|
|
||||||
我们设想一下,我们是通过 nums[j] 和 nums[j+1] 进行比较,如果大于则进行交换,那我们设想一下,如果一个完全有序的数组,我们进行冒泡排序,每次比较发现都不用进行交换。
|
|
||||||
|
|
||||||
那么如果没有交换则说明当前完全有序。那我们可不可以通过一个标志位来进行判断是否发生了交换呢?当然是可以的
|
|
||||||
|
|
||||||
我们来对冒泡排序进行改进
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
int len = nums.length;
|
|
||||||
//标志位
|
|
||||||
boolean flag = true;
|
|
||||||
//注意看 for 循环条件
|
|
||||||
for (int i = 0; i < len && flag; ++i) {
|
|
||||||
//如果没发生交换,则依旧为false,下次就会跳出循环
|
|
||||||
flag = false;
|
|
||||||
for (int j = 0; j < len - i - 1; ++j) {
|
|
||||||
if (nums[j] > nums[j+1]) {
|
|
||||||
swap(nums,j,j+1);
|
|
||||||
//发生交换,则变为true,下次继续判断
|
|
||||||
flag = true;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
|
|
||||||
}
|
|
||||||
public void swap(int[] nums,int i,int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
这样我们就避免掉了已经有序的情况下无意义的循环判断。
|
|
||||||
|
|
||||||
**冒泡排序时间复杂度分析**
|
|
||||||
|
|
||||||
最好情况,就是要排序的表完全有序的情况下,根据改进后的代码,我们只需要一次遍历即可,
|
|
||||||
|
|
||||||
只需 n -1 次比较,时间复杂度为 O(n)。最坏情况时,即待排序表逆序的情况,则需要比较(n-1) + (n-2) +.... + 2 + 1= n*(n-1)/2 ,并等量级的交换,则时间复杂度为O(n^2)。*
|
|
||||||
|
|
||||||
*平均情况下,需要 n*(n-1)/4 次交换操作,比较操作大于等于交换操作,而复杂度的上限是 O(n^2),所以平均情况下的时间复杂度就是 O(n^2)。
|
|
||||||
|
|
||||||
**冒泡排序空间复杂度分析**
|
|
||||||
|
|
||||||
因为冒泡排序只是相邻元素之间的交换操作,只用到了常量级的额外空间,所以空间复杂度为 O(1)
|
|
||||||
|
|
||||||
**冒泡排序稳定性分析**
|
|
||||||
|
|
||||||
那么冒泡排序是稳定的吗?当然是稳定的,我们代码中,当 nums[j] > nums[j + 1] 时,才会进行交换,相等时不会交换,相等元素的相对位置没有改变,所以冒泡排序是稳定的。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|
|
||||||
| -------- | -------------- | -------------- | -------------- | ---------- | -------- |
|
|
||||||
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
|
|
||||||
|
|
||||||
@ -1,203 +0,0 @@
|
|||||||
之前我们说过了如何利用快速排序解决荷兰国旗问题,下面我们看下这两个题目
|
|
||||||
|
|
||||||
**剑指 Offer 45. 把数组排成最小的数**,**leetcode 179 最大数**
|
|
||||||
|
|
||||||
这两个问题根本上也是排序问题,下面我们一起来看一下题目描述
|
|
||||||
|
|
||||||
输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
|
|
||||||
|
|
||||||
示例 1:
|
|
||||||
|
|
||||||
> 输入: [10,2]
|
|
||||||
> 输出: "102"
|
|
||||||
|
|
||||||
示例 2:
|
|
||||||
|
|
||||||
> 输入: [3,30,34,5,9]
|
|
||||||
> 输出: "3033459"
|
|
||||||
|
|
||||||
题目很容易理解,就是让我们找出拼接的所有数字中最小的一个,但是我们需要注意的是,因为输出结果较大,所以我们不能返回 int 应该将数字转换成字符串,所以这类问题还是隐形的大数问题。
|
|
||||||
|
|
||||||
我们看到这个题目时,可能想到的是这种解题思路,我们首先求出数组中所有数字的全排列,然后将排列拼起来,最后再从中取出最小的值,但是我们共有 n 个数,则有 n !个排列,显然数目是十分庞大的,那么我们有没有其他更高效的方法呢?
|
|
||||||
|
|
||||||
大家先来思考一下这个问题。
|
|
||||||
|
|
||||||
我们假设两个数字 m , n 可以拼接成 mn 和 nm 那么我们怎么返回最小的那个数字呢?
|
|
||||||
|
|
||||||
我们需要比较 mn 和 nm ,假设 mn < nm 则此时我们求得的最小数字就是 mn
|
|
||||||
|
|
||||||
> 注:mn 代表 m 和 n 进行拼接,例如 m = 10, n = 1,mn = 101
|
|
||||||
|
|
||||||
当 mn < nm 时,得到最小数字 mn, 因为在最小数字 mn 中 ,m 排在 n 的前面,我们此时定义 m "小于" n。
|
|
||||||
|
|
||||||
**注意:此时的 "小于" ,并不是数值的 < 。是我们自己定义,因为 m 在最小数字 mn 中位于 n 的前面,所以我们定义 m 小于 n。**
|
|
||||||
|
|
||||||
下面我们通过一个例子来加深下理解。
|
|
||||||
|
|
||||||
假设 m = 10,n = 1 则有 mn = 101 和 nm = 110
|
|
||||||
|
|
||||||
我们比较 101 和 110 ,发现 101 < 110 所以此时我们的最小数字为 101 ,又因为在最小数字中 10 (m) 排在 1(n) 的前面,我们根据定义则是 10 “小于” 1,反之亦然。
|
|
||||||
|
|
||||||
这时我们自己定义了一种新的,比较两个数字大小的规则,但是我们怎么保证这种规则是有效的?
|
|
||||||
|
|
||||||
怎么能确保通过这种规则,拼接数组中**所有数字**(我们之前仅仅是通过两个数字进行举例),得到的数就是最小的数字呢?
|
|
||||||
|
|
||||||
下面我们先来证明下规则的有效性
|
|
||||||
|
|
||||||
注:为了便于分辨我们用 A,B,C 表示元素, a,b,c 表示元素用十进制表示时的位数
|
|
||||||
|
|
||||||
(1)自反性:AA = AA,所以 A 等于 A
|
|
||||||
|
|
||||||
(2)对称性:如果 A "小于" B 则 AB < BA,所以 BA > AB 则 B "大于" A
|
|
||||||
|
|
||||||
(3)传递性:传递性的证明稍微有点复杂,大家记得认真阅读。
|
|
||||||
|
|
||||||
如果 A“小于” B,则 AB < BA, 假设 A 和 B 用十进制表示时分别有 a 位和 b 位
|
|
||||||
|
|
||||||
则 AB = A * 10 ^ b + B , BA = B * 10 ^ a + A
|
|
||||||
|
|
||||||
> 例 A = 10, a = 2 (两位数) B = 1, b = 1 (一位数)
|
|
||||||
>
|
|
||||||
> AB = A * 10 ^ b + B = 10 * 10 ^ 1 + 1 = 101
|
|
||||||
>
|
|
||||||
> BA = B * 10 ^ a + A = 1 * 10 ^ 2 + 10 = 110
|
|
||||||
|
|
||||||
AB < BA 则 **A * 10 ^ b + B < BA = B * 10 ^ a + A** 整理得
|
|
||||||
|
|
||||||
A / (10^a - 1) < B / (10 ^ b - 1)
|
|
||||||
|
|
||||||
同理,如果 B “小于” C 则 BC < CB ,C 用十进制表示时有 c 位,和前面推导过程一样
|
|
||||||
|
|
||||||
BC = B * 10 ^ c + C
|
|
||||||
|
|
||||||
CB = C * 10 ^ b + B
|
|
||||||
|
|
||||||
BC < CB 整理得 B / (10 ^ b - 1) < C / (10 ^ c - 1);
|
|
||||||
|
|
||||||
我们通过 A / (10 ^ a - 1) < B / (10 ^ b - 1) ,B / (10 ^ b - 1) < C / (10 ^ c - 1);
|
|
||||||
|
|
||||||
可以得到 A / (10^a - 1) < C / (10 ^ c - 1)
|
|
||||||
|
|
||||||
则可以得到 AC < CA 即 A “小于” C
|
|
||||||
|
|
||||||
传递性证得。
|
|
||||||
|
|
||||||
我们通过上面的证明过程知道了我们定义的规则,满足自反性,对称性,传递性,则说明规则是有效的。
|
|
||||||
|
|
||||||
接下来我们证明,利用这种规则得到的数字,的确是最小的。我们利用反证法来进行证明
|
|
||||||
|
|
||||||
我们先来回顾一下我们之前定义的规则
|
|
||||||
|
|
||||||
> 当 mn < nm 时,得到最小数字 mn, 因为在最小数字 mn 中 ,m 排在 n 的前面,
|
|
||||||
>
|
|
||||||
> 我们此时定义 m "小于" n。
|
|
||||||
|
|
||||||
我们假设我们根据上诉规则得到的数字为 xxxxxxxx
|
|
||||||
|
|
||||||
存在这么一对字符串 A B ,虽然 AB < BA, 按照规则 A 应该排在 B 的前面,但是在最后结果中 A 排在 B 的后面。则此时共有这么几种情况
|
|
||||||
|
|
||||||
见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
其实我们可以归结为两大类, B 和 A 之间没有其他值, B 和 A 之间有其他值。
|
|
||||||
|
|
||||||
我们先来看**没有其他值**的情况
|
|
||||||
|
|
||||||
假设我们求得的最小值为 XXXXBA, 虽然 A "小于" B,但是在最后结果中 B 排在了 A 的前面,这和我们之前定义的规则是冲突的,大家思考一下这个值为最小值吗?
|
|
||||||
|
|
||||||
假设 XXXXBA为最小值,但是因为 A "小于" B ,则 AB < BA ,
|
|
||||||
|
|
||||||
所以 XXXXAB 一定小于 XXXXBA 。
|
|
||||||
|
|
||||||
和我们之前的假设矛盾。
|
|
||||||
|
|
||||||
当然 BAXXXX 也一样。
|
|
||||||
|
|
||||||
下面我们来看当 B 和 A 之间有其他值的情况
|
|
||||||
|
|
||||||
即 BXXXXA
|
|
||||||
|
|
||||||
我们可以将 XXXX 看成一个字符串 C,则为 BCA
|
|
||||||
|
|
||||||
因为求得的最小值为 BCA ,
|
|
||||||
|
|
||||||
在最小值 BCA 中 B 在 C 的前面,C 在 A 的前面,
|
|
||||||
|
|
||||||
则 BC < CB, CA < AC,B "小于 C", C “小于” A
|
|
||||||
|
|
||||||
根据我们之前证明的传递性
|
|
||||||
|
|
||||||
则 B "小于" A
|
|
||||||
|
|
||||||
但是我们假设是 A “小于” B ,与假设冲突,证得
|
|
||||||
|
|
||||||
综上所述,得出假设不成立,从而得出结论:对于排成的最小数字,不存在满足下述关系的一对字符串:虽然 A "小于" B , 但是在最后结果中 B 排在了 A 的前面.
|
|
||||||
|
|
||||||
好啦,我们证明我们定义的规则有效下面我们直接看代码吧。继续使用我们的三向切分来解决
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public String minNumber(int[] nums) {
|
|
||||||
String[] arr = new String[nums.length];
|
|
||||||
//解决大数问题,将数字转换为字符串
|
|
||||||
for (int i = 0 ; i < nums.length; ++i) {
|
|
||||||
arr[i] = String.valueOf(nums[i]);
|
|
||||||
}
|
|
||||||
|
|
||||||
quickSort(arr,0,arr.length-1);
|
|
||||||
StringBuffer str = new StringBuffer();
|
|
||||||
|
|
||||||
for (String x : arr) {
|
|
||||||
str.append(x);
|
|
||||||
}
|
|
||||||
return str.toString();
|
|
||||||
}
|
|
||||||
public void quickSort(String[] arr, int left, int right) {
|
|
||||||
if (left >= right) {
|
|
||||||
return;
|
|
||||||
}
|
|
||||||
int low = left;
|
|
||||||
int hight = right;
|
|
||||||
int i = low+1;
|
|
||||||
String pivot = arr[low];
|
|
||||||
|
|
||||||
while (i <= hight) {
|
|
||||||
//比较大小
|
|
||||||
if ((pivot+arr[i]).compareTo(arr[i]+pivot) > 0 ) {
|
|
||||||
swap(arr,i++,low++);
|
|
||||||
} else if ((pivot+arr[i]).compareTo(arr[i]+pivot) < 0) {
|
|
||||||
swap(arr,i,hight--);
|
|
||||||
} else {
|
|
||||||
i++;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
quickSort(arr,left,low-1);
|
|
||||||
quickSort(arr,hight+1,right);
|
|
||||||
|
|
||||||
}
|
|
||||||
public void swap(String[] arr, int i, int j) {
|
|
||||||
String temp = arr[i];
|
|
||||||
arr[i] = arr[j];
|
|
||||||
arr[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
@ -1,259 +0,0 @@
|
|||||||
### **堆排序**
|
|
||||||
|
|
||||||
说堆排序之前,我们先简单了解一些什么是堆?堆这种数据结构应用场景非常多,所以我们需要熟练掌握呀!
|
|
||||||
|
|
||||||
那我们了解堆之前,先来简单了解下,什么是完全二叉树?
|
|
||||||
|
|
||||||
我们来看下百度百科的定义,完全二叉树:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
|
|
||||||
|
|
||||||
哦!我们可以这样理解,除了最后一层,其他层的节点个数都是满的,而且最后一层的叶子节点必须靠左。
|
|
||||||
|
|
||||||
下面我们来看一下这几个例子
|
|
||||||
|
|
||||||
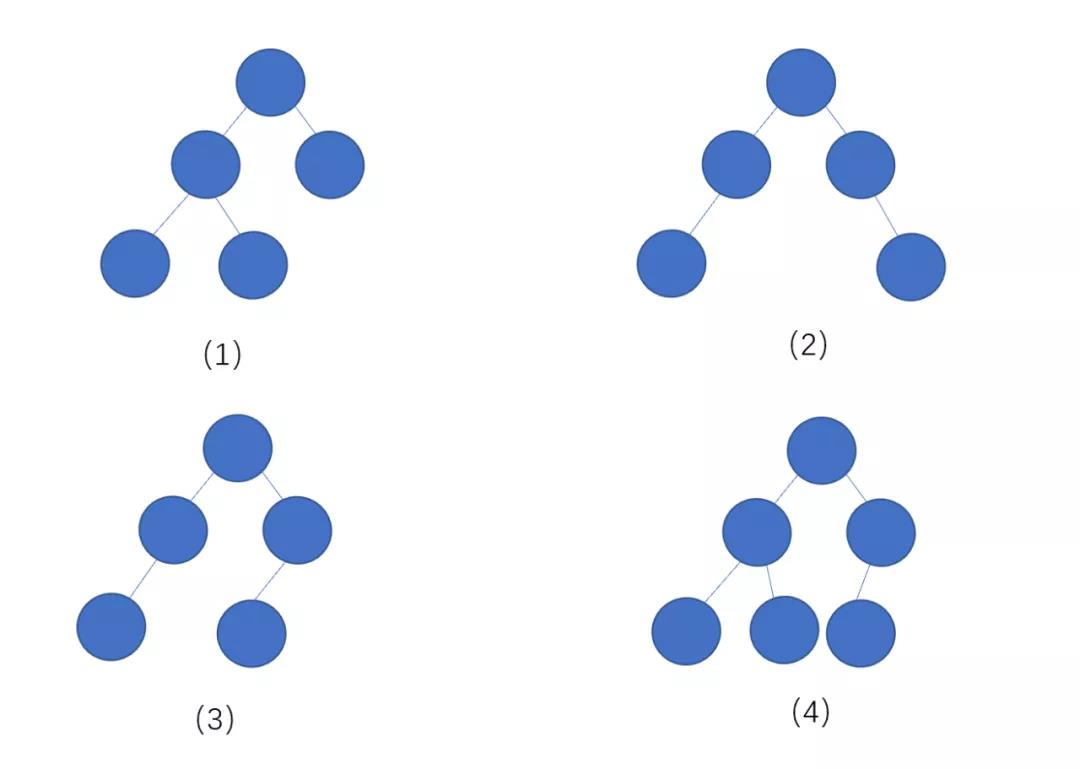
|
|
||||||
|
|
||||||
上面的几个例子中,(1)(4)为完全二叉树,(2)(3)不是完全二叉树,通过上面的几个例子,我们了解了什么是完全二叉树,
|
|
||||||
|
|
||||||
那么堆到底是什么呢?
|
|
||||||
|
|
||||||
下面我们来看一下二叉堆的要求
|
|
||||||
|
|
||||||
(1)必须是完全二叉树
|
|
||||||
|
|
||||||
(2)二叉堆中的每一个节点,都必须大于等于(或小于等于)其子树中每个节点的值。
|
|
||||||
|
|
||||||
若是每个节点大于等于子树中的每个节点,我们称之为大顶堆,小于等于子树中的每个节点,我们则称之为小顶堆。见下图
|
|
||||||
|
|
||||||
下面我们再来看一下二叉堆的具体例子。
|
|
||||||
|
|
||||||
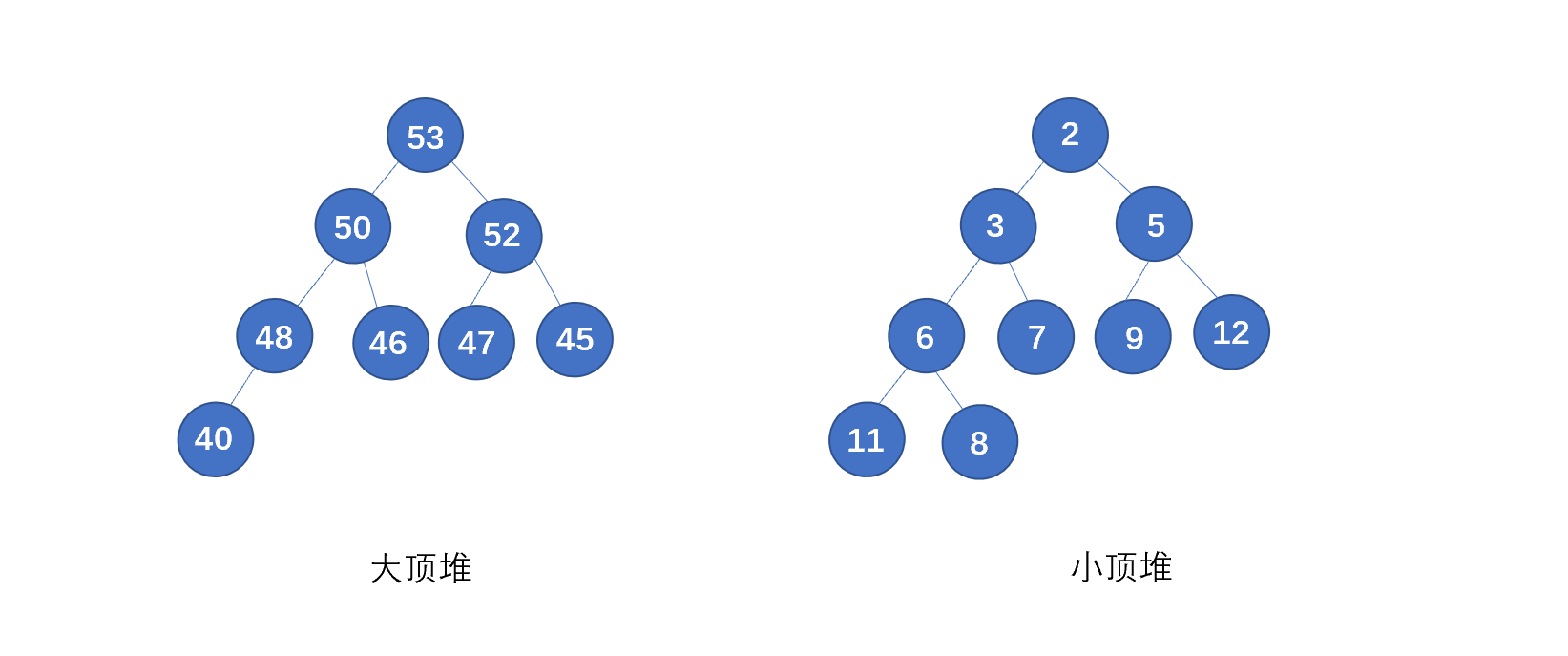
|
|
||||||
|
|
||||||
上图则为大顶堆和小顶堆,我们再来回顾一下堆的要求,看下是否符合
|
|
||||||
|
|
||||||
(1)必须是完全二叉树
|
|
||||||
|
|
||||||
(2)堆中的每一个节点,都必须大于等于(或小于等于)其子树中每个节点的值。
|
|
||||||
|
|
||||||
好啦,到这里我们已经完全掌握二叉堆了,那么二叉堆又是怎么存储的呢?因为堆是完全二叉树,所以我们完全可以用数组存储。具体思想见下图,我们仅仅按照顺序将节点存入数组即可,我们通过小顶堆进行演示。
|
|
||||||
|
|
||||||
注:我们是从下标 1 开始存储的,这样能省略一些计算,下文中我们将二叉堆简称为堆
|
|
||||||
|
|
||||||
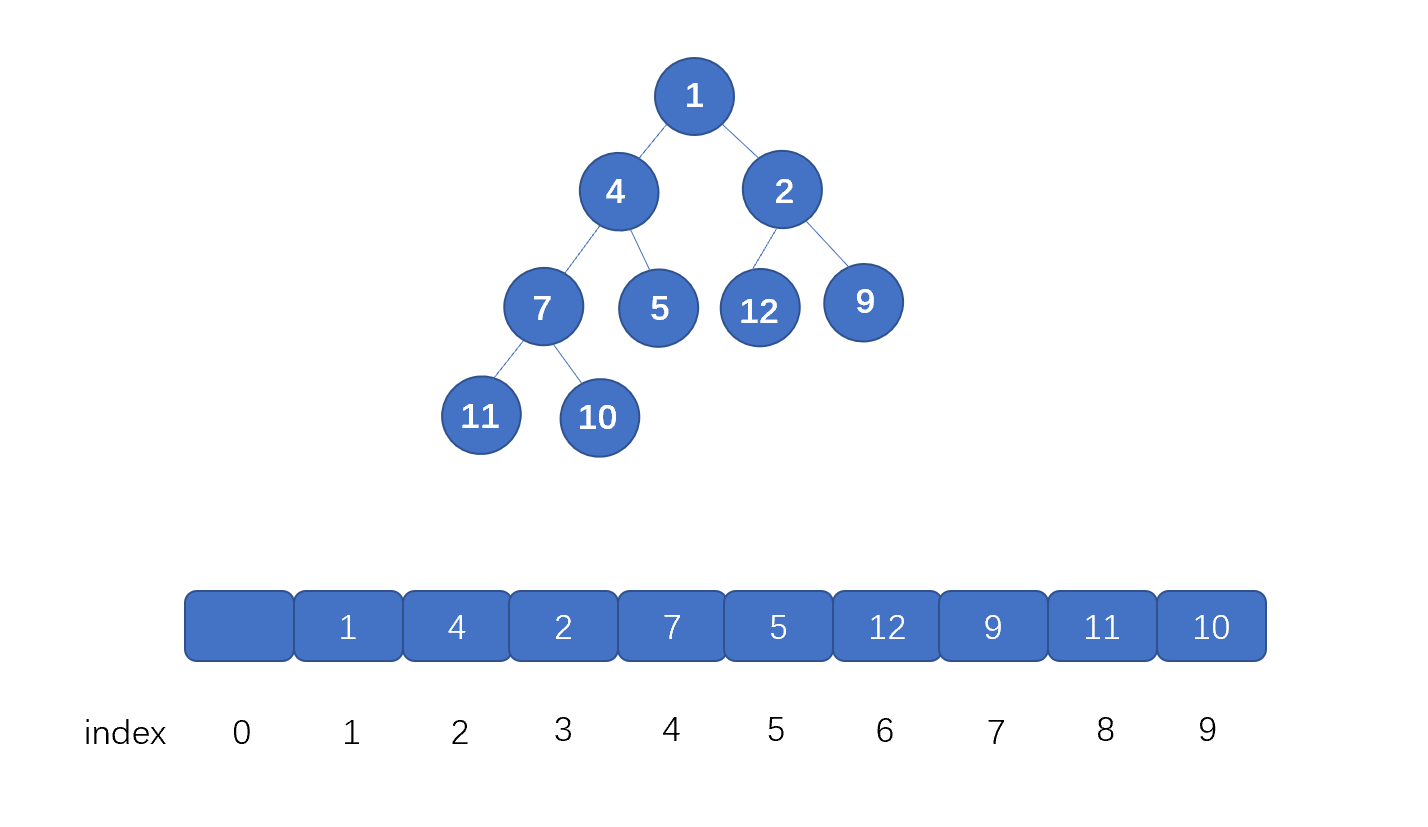
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们来看一下为什么我们可以用数组来存储堆呢?
|
|
||||||
|
|
||||||
我们首先看根节点,也就是值为 1 的节点,它在数组中的下标为 1 ,它的左子节点,也就是值为 4 的节点,此时索引为 2,右子节点也就是值为 2 的节点,它的索引为 3。
|
|
||||||
|
|
||||||
我们发现其中的关系了吗?
|
|
||||||
|
|
||||||
数组中,某节点(非叶子节点)的下标为 i , 那么其**左子节点下标为 2*i** (这里可以直接通过相乘得到左孩子,如果从0 开始存,需要 2*i+1 才行), 右子节点为 2*i+1**,**其父节点为 i/2 。既然我们完全可以根据索引找到某节点的 **左子节点** 和 **右子节点**,那么我们用数组存储是完全没有问题的。
|
|
||||||
|
|
||||||
好啦,我们知道了什么是堆和如何用数组存储堆,那我们如何完成堆排序呢?
|
|
||||||
|
|
||||||
堆排序其实主要有两个步骤
|
|
||||||
|
|
||||||
- 建堆
|
|
||||||
- 排序
|
|
||||||
|
|
||||||
下面我们先来了解下建堆
|
|
||||||
|
|
||||||
我们刚才说了用数组来存储大顶(小顶)堆,此时的元素已经满足某节点大于等于(或小于等于)子树节点,但是随机给我们一个数组,此时并不一定满足上诉要求,所以我们需要调整数组,使其满足大顶堆或小顶堆的要求。这个就是堆化,也可以称其为建堆。
|
|
||||||
|
|
||||||
建堆我们这里提出两种方法,利用上浮操作,也就是不断插入元素进行建堆,另一种是利用下沉操作,遍历父节点,不断将其下沉,进行建堆,我们一起来看吧。
|
|
||||||
|
|
||||||
我们先来说下第一种建堆方式
|
|
||||||
|
|
||||||
**利用上浮操作建堆**
|
|
||||||
|
|
||||||
说之前我们先来了解下,如何往已经建好的堆里,插入新的元素,我们直接看例子吧,一下就懂啦。
|
|
||||||
|
|
||||||
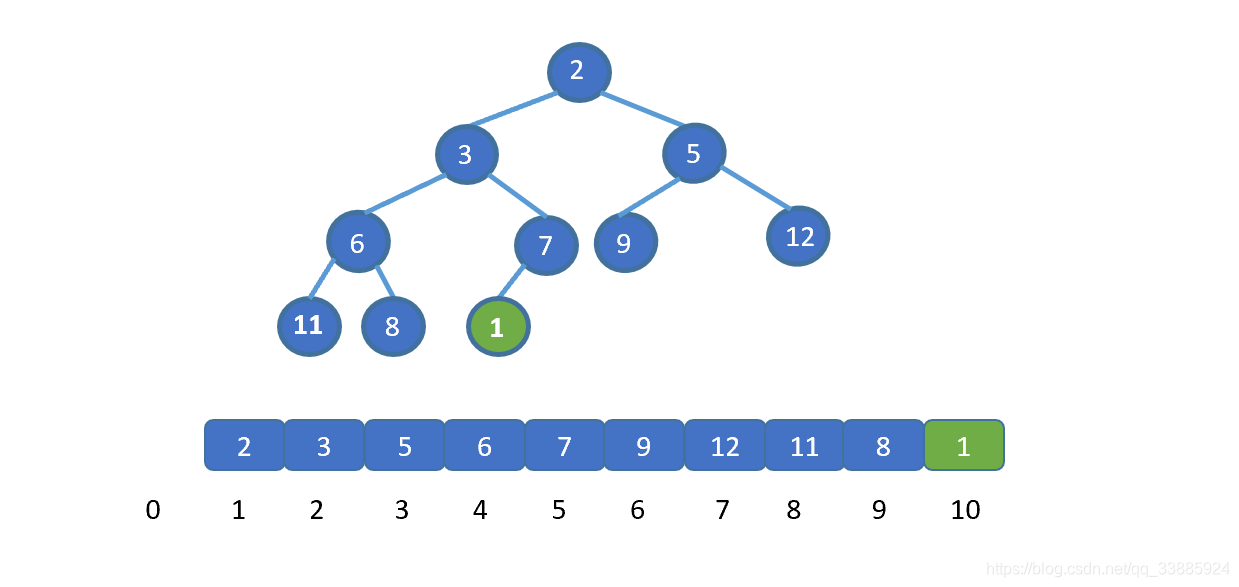
|
|
||||||
|
|
||||||
假设让我们插入新的元素 1 (绿色节点),我们发现此时 1 小于其父节点 的值 7 ,并不遵守小顶堆的规则,那我们则需要移动元素 1 。让 1 与 7 交换,(如果新插入元素大于父节点的值,则说明插入新节点后仍满足小顶堆规则,无需交换)。
|
|
||||||
|
|
||||||
之前我们说过,我们可以用数组保存堆,并且可以通过 i/2 得到其父节点的值,那么此时我们就明白怎么做啦。
|
|
||||||
|
|
||||||
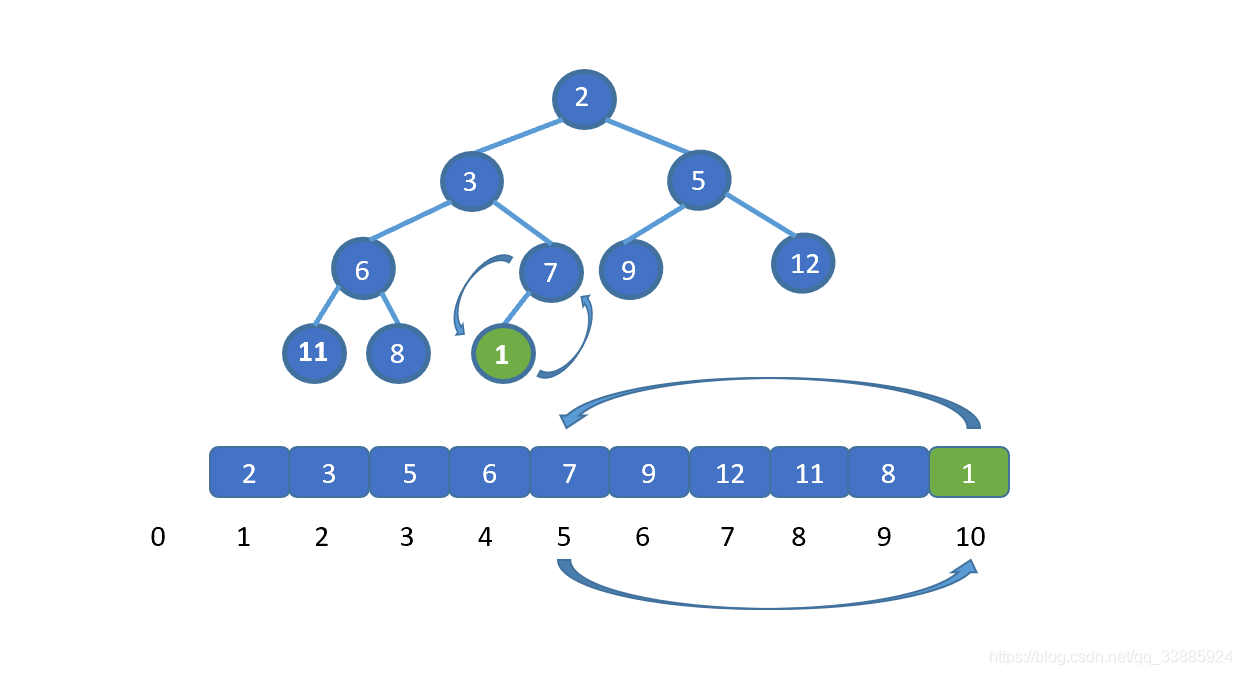
|
|
||||||
|
|
||||||
将插入节点与其父节点,交换。
|
|
||||||
|
|
||||||
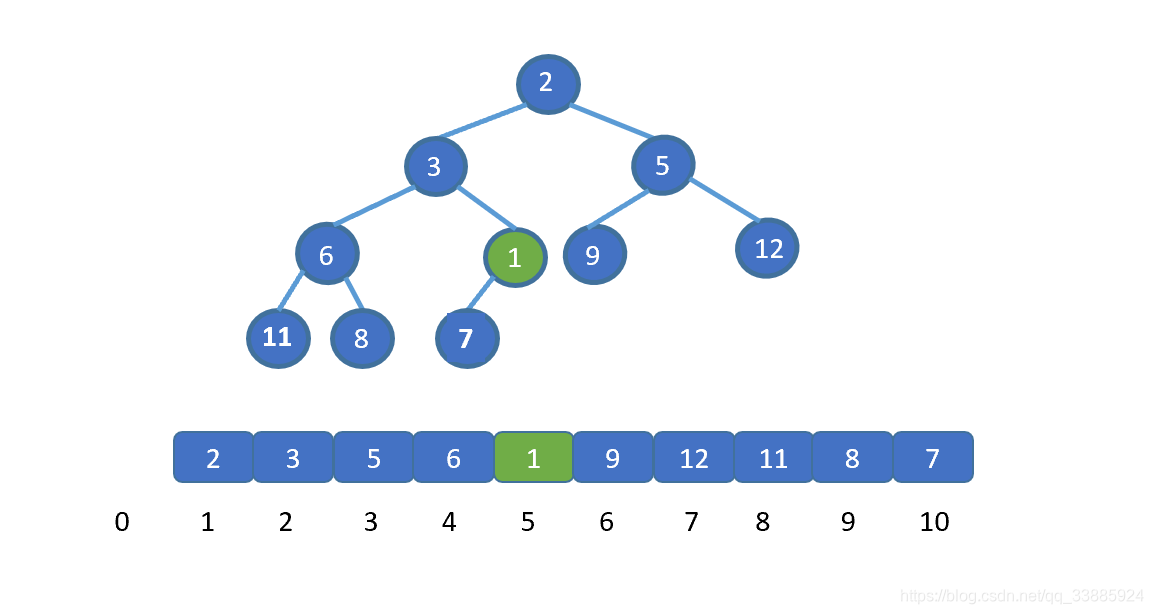
|
|
||||||
|
|
||||||
交换之后,我们继续将新插入元素,也就是 1 与其父节点比较,如果大于其父节点,则无需交换,循环结束。若小于则需要继续交换,直到 1 到达适合他的地方。大家是不是已经直到该怎么做啦!下面我们直接看动图吧。
|
|
||||||
|
|
||||||
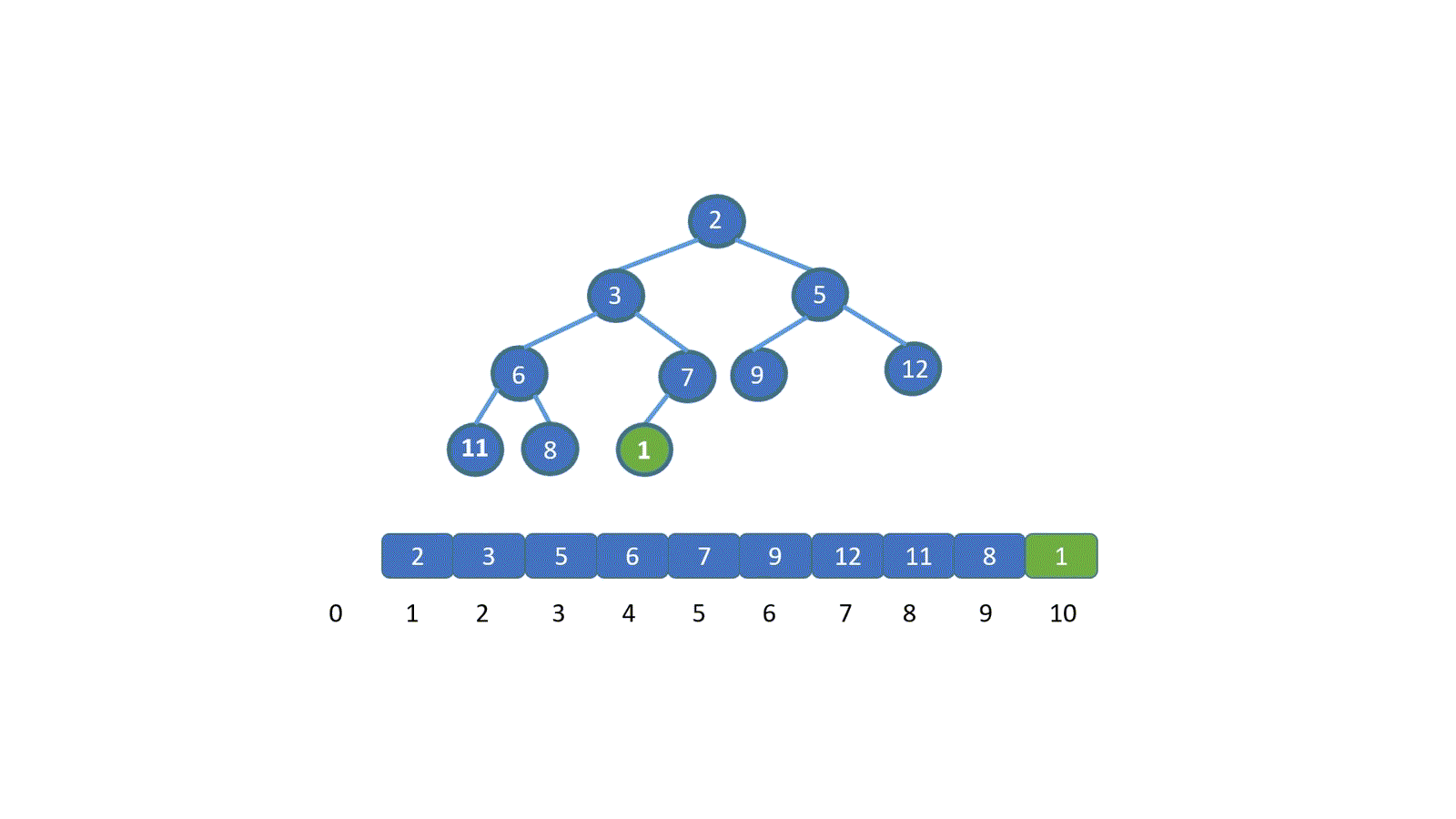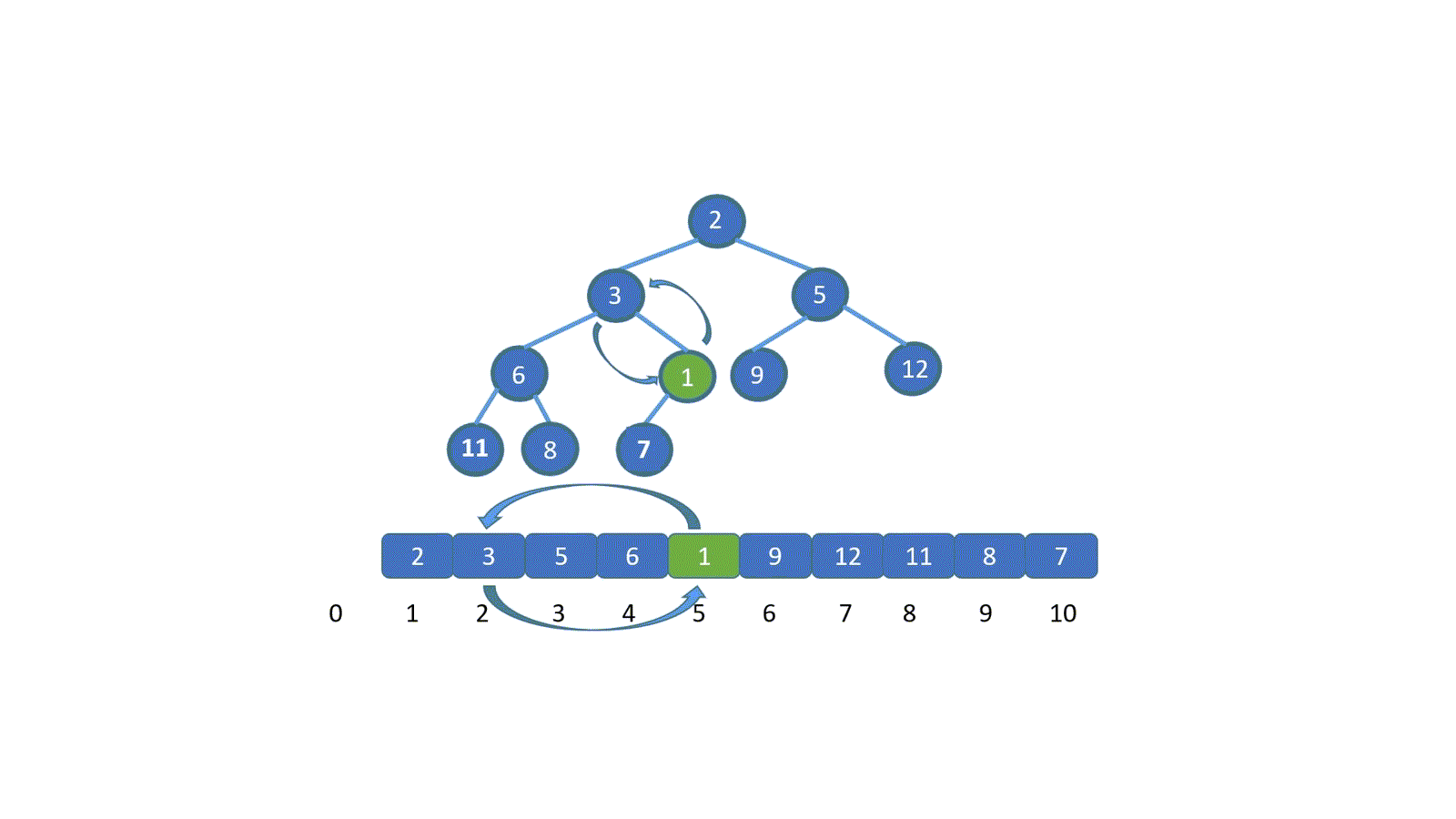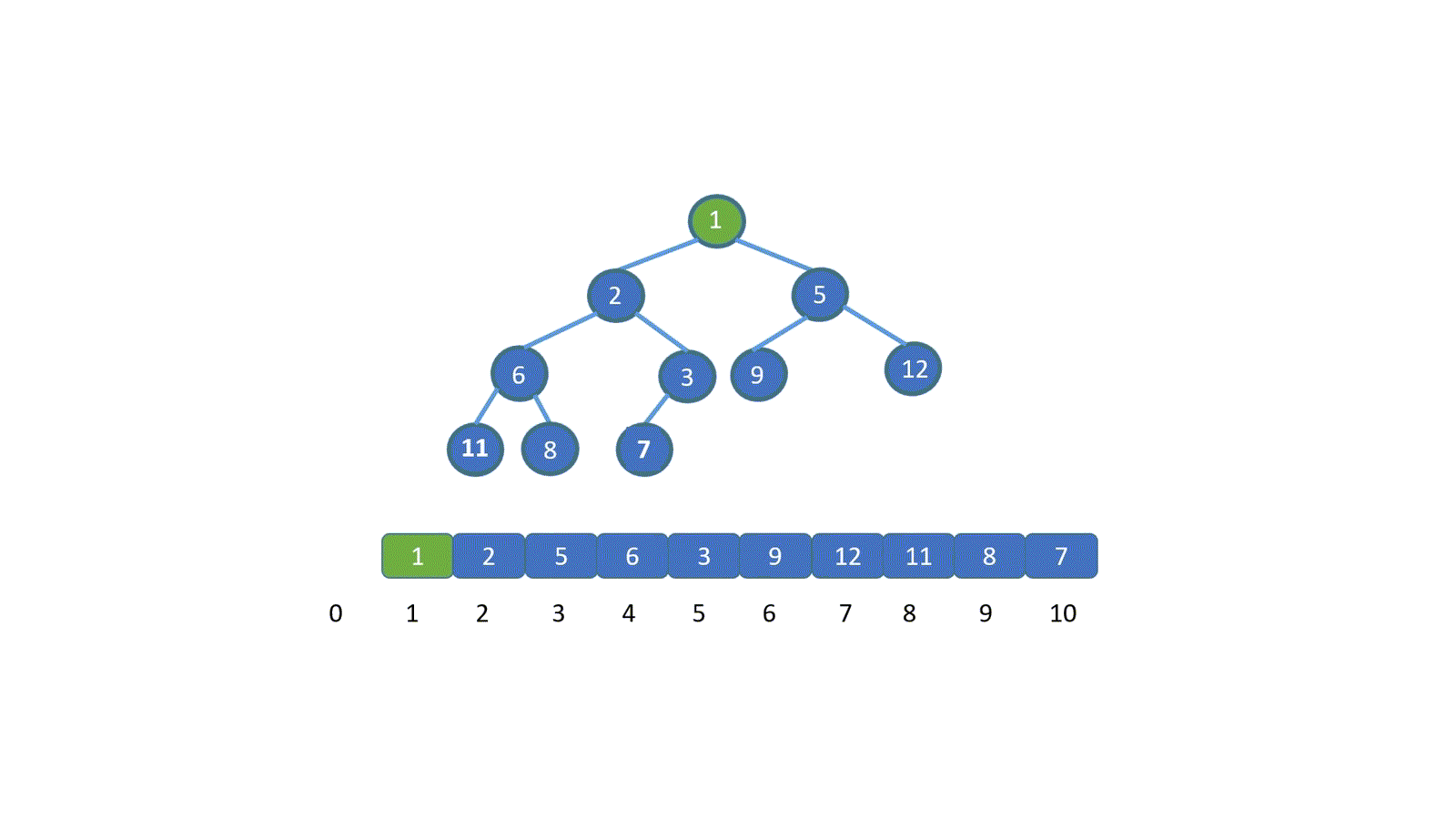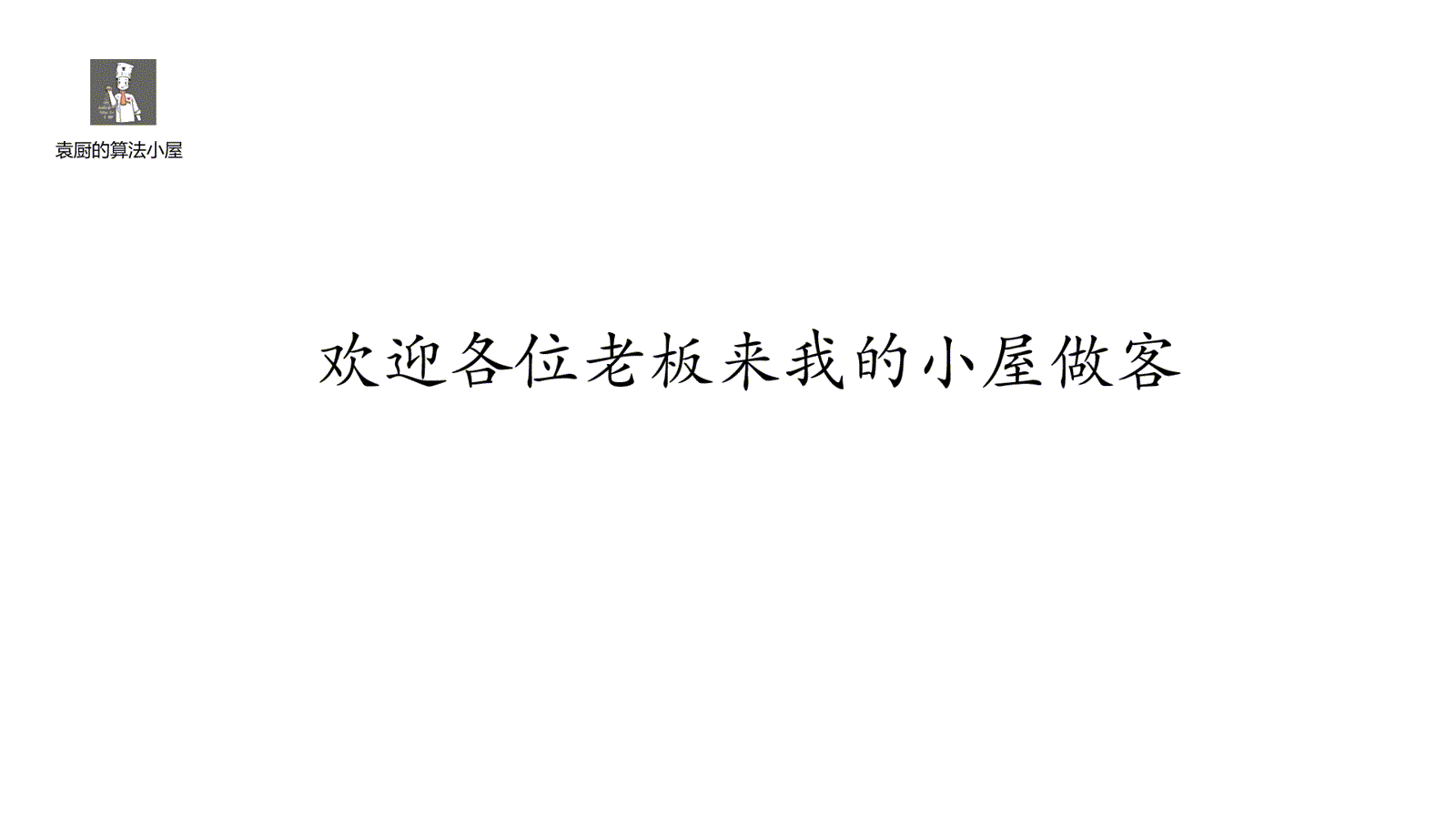
|
|
||||||
|
|
||||||
看完动图是不是就妥了,其实很简单,我们只需将新加入元素与其父节点比较,判断是否小于堆顶元素(小顶堆),如果小于则进行交换,(让更小的节点为父节点)直到符合堆的规则位置,大顶堆则相反。
|
|
||||||
|
|
||||||
**我们发现,我们新插入的元素是不是一层层的上浮,直到找到属于自己的位置,我们将这个操作称之为上浮操作。**
|
|
||||||
|
|
||||||
那我们知道了上浮,岂不是就可以实现建堆了?是的,我们则可以依次遍历数组,就好比不断往堆中插入新元素,直至遍历结束,这样我们就完成了建堆,这种方法当然是可以的。
|
|
||||||
|
|
||||||
我们一起来看一下上浮操作代码。
|
|
||||||
|
|
||||||
```java
|
|
||||||
public void swim (int index) {
|
|
||||||
while (index > 1 && nums[index/2] > nums[index]) {
|
|
||||||
swap(index/2,index);//交换
|
|
||||||
index = index/2;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
既然利用上浮操作建堆已经搞懂啦,那么我们再来了解一下,利用下沉操作建堆吧,也很容易理解。
|
|
||||||
|
|
||||||
给我们一个无序数组(不满足堆的要求),见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们发现,7 位于堆顶,但是此时并不满足小顶堆的要求,我们需要把 7 放到属于它的位置,我们应该怎么做呢?
|
|
||||||
|
|
||||||
废话不多说,我们先来看视频模拟,看完保准可以懂
|
|
||||||
|
|
||||||
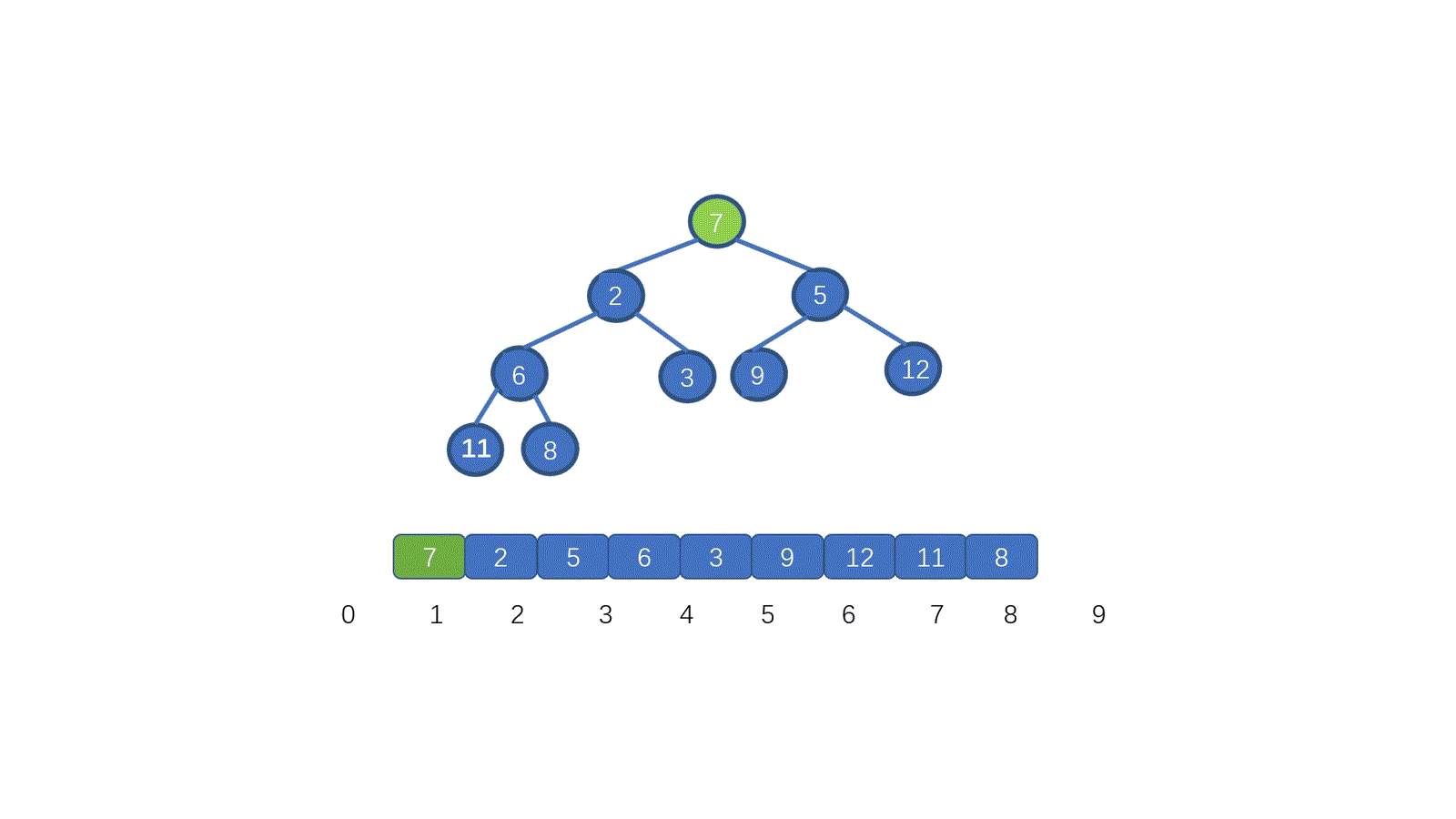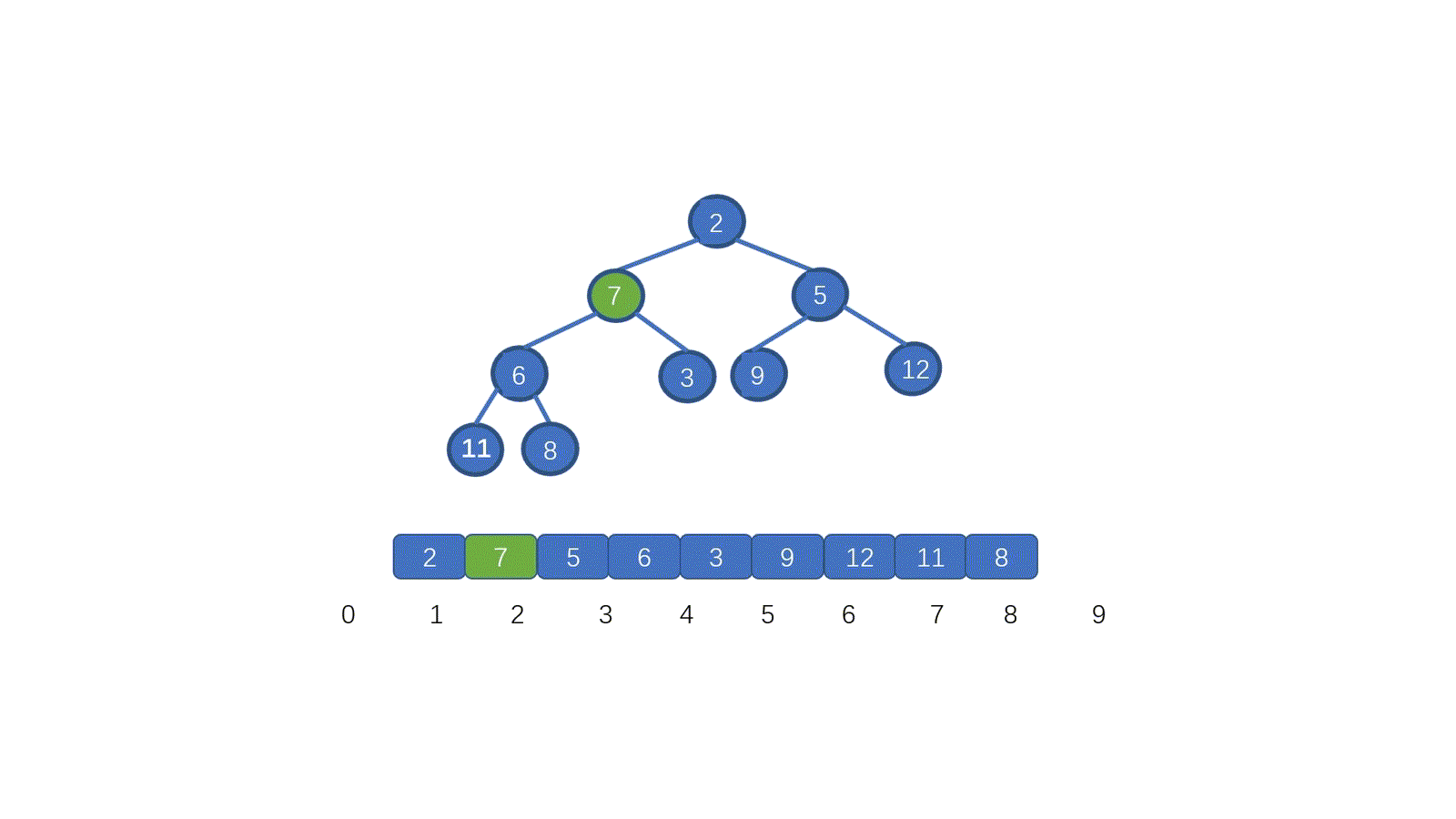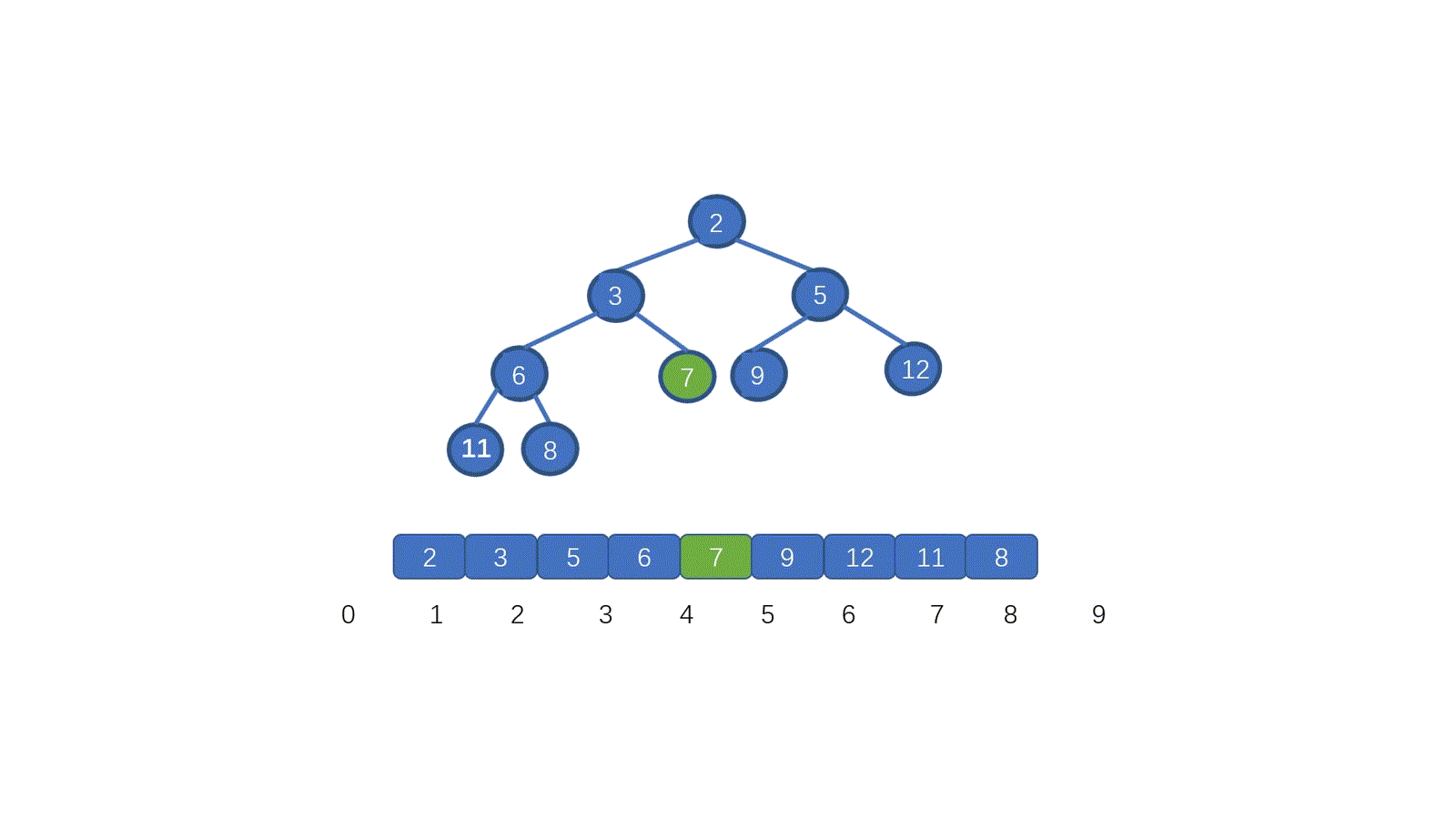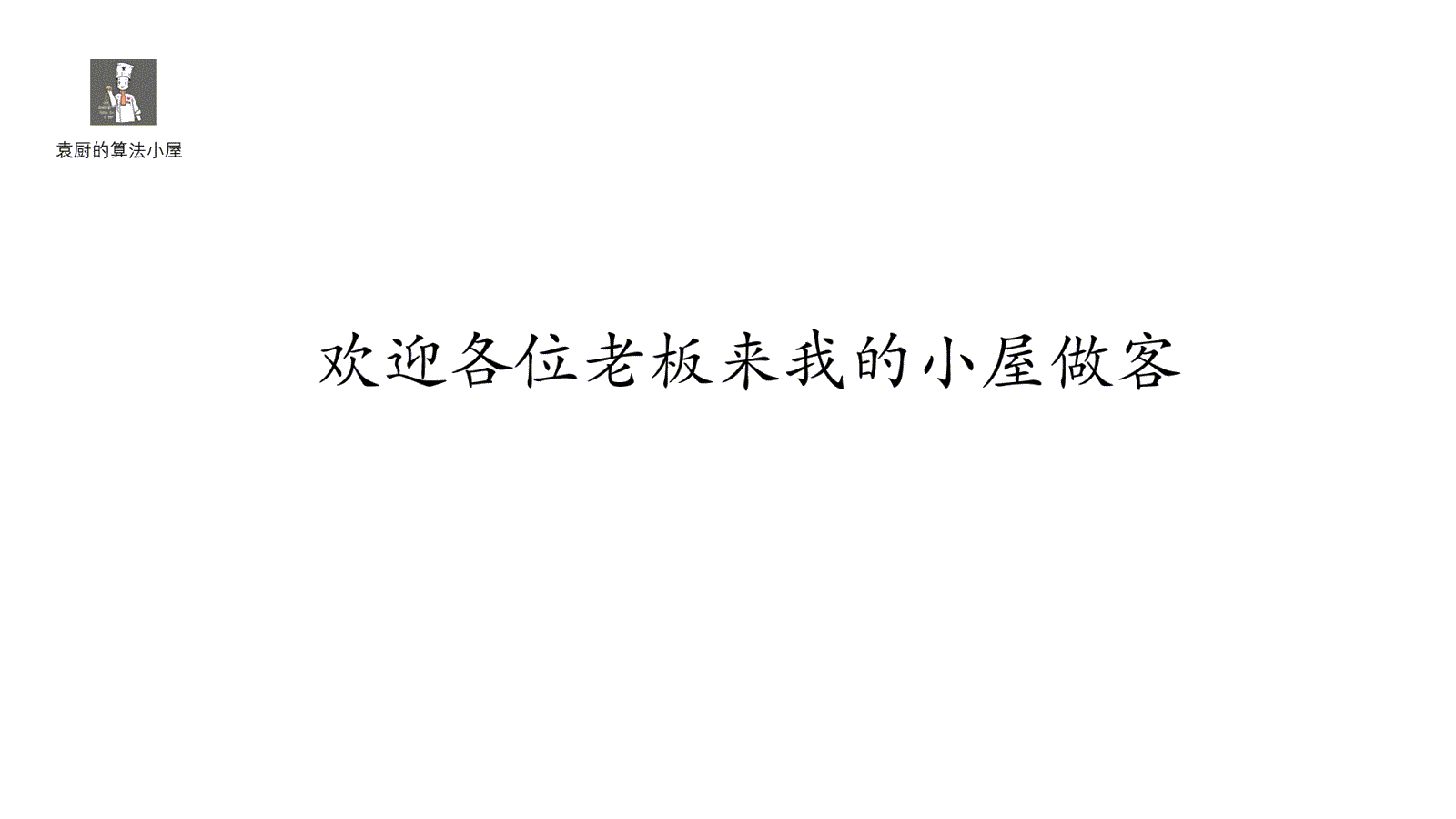
|
|
||||||
|
|
||||||
看完视频是不是懂个大概了,但是不知道大家有没有注意到这个地方。为什么 7 第一次与其左孩子节点 2 交换,第二次与右孩子节点 3 交换。见下图
|
|
||||||
|
|
||||||
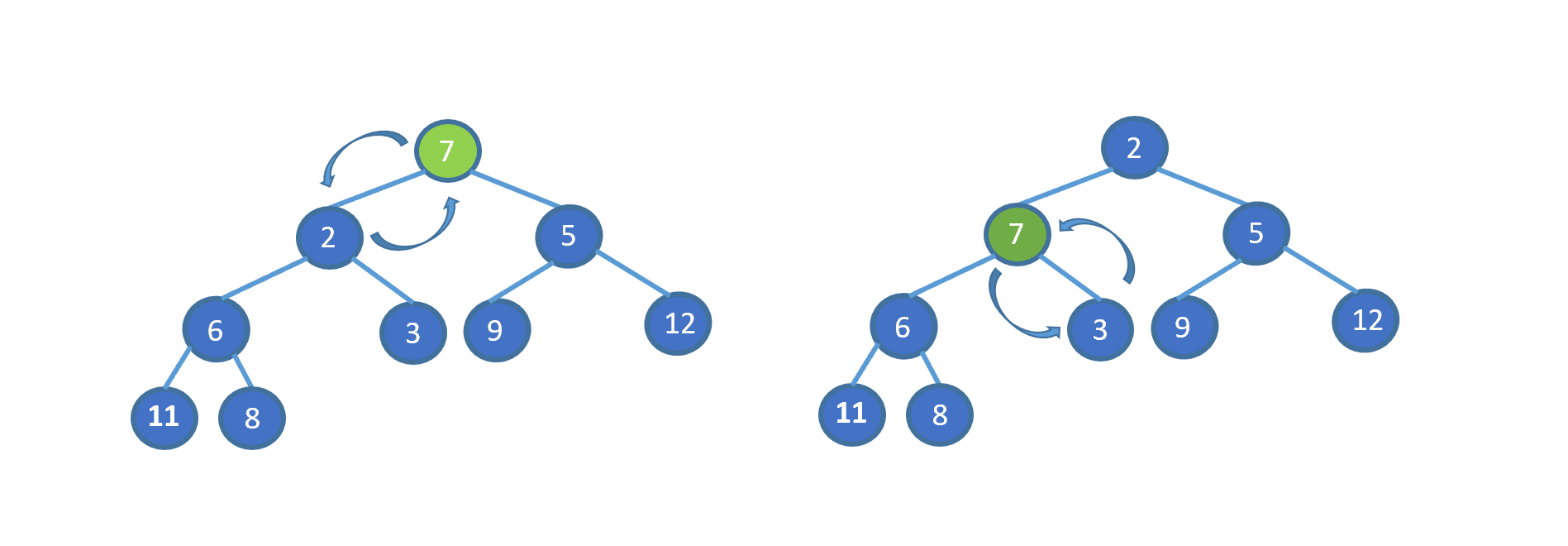
|
|
||||||
|
|
||||||
其实很容易理解,我们需要与孩子节点中最小的那个交换,因为我们需要交换后,父节点小于两个孩子节点,如果我们第一步,7 与 5 进行交换的话,则同样不能满足小顶堆。
|
|
||||||
|
|
||||||
那我们怎么判断节点找到属于它的位置了呢?主要有两个情况
|
|
||||||
|
|
||||||
- 待下沉元素小于(大于)两个子节点,此时符合堆的规则,无序下沉,例如上图中的 6
|
|
||||||
- 下沉为叶子节点,此时没有子节点,例如 7 下沉到最后变成了叶子节点。
|
|
||||||
|
|
||||||
我们将上面的操作称之为下沉操作。
|
|
||||||
|
|
||||||
这时我们又有疑问了,下沉操作我懂了,但是这跟建堆有个锤子关系啊!
|
|
||||||
|
|
||||||
不要急,我们继续来看视频,这次我们通过下沉操作建个大顶堆。
|
|
||||||
|
|
||||||
> **初始数组 [8,5,7,9,2,10,1,4,6,3]**
|
|
||||||
|
|
||||||
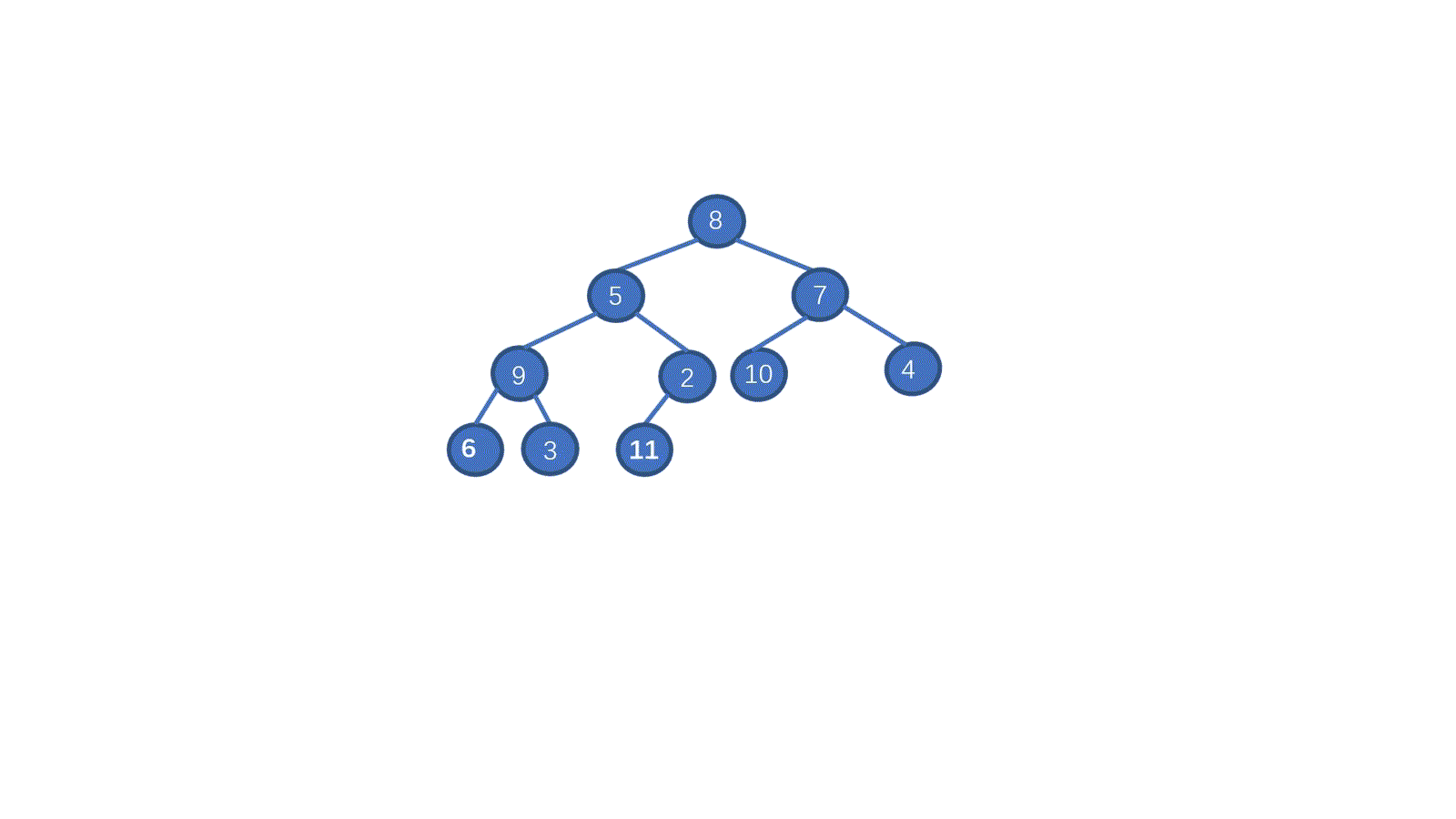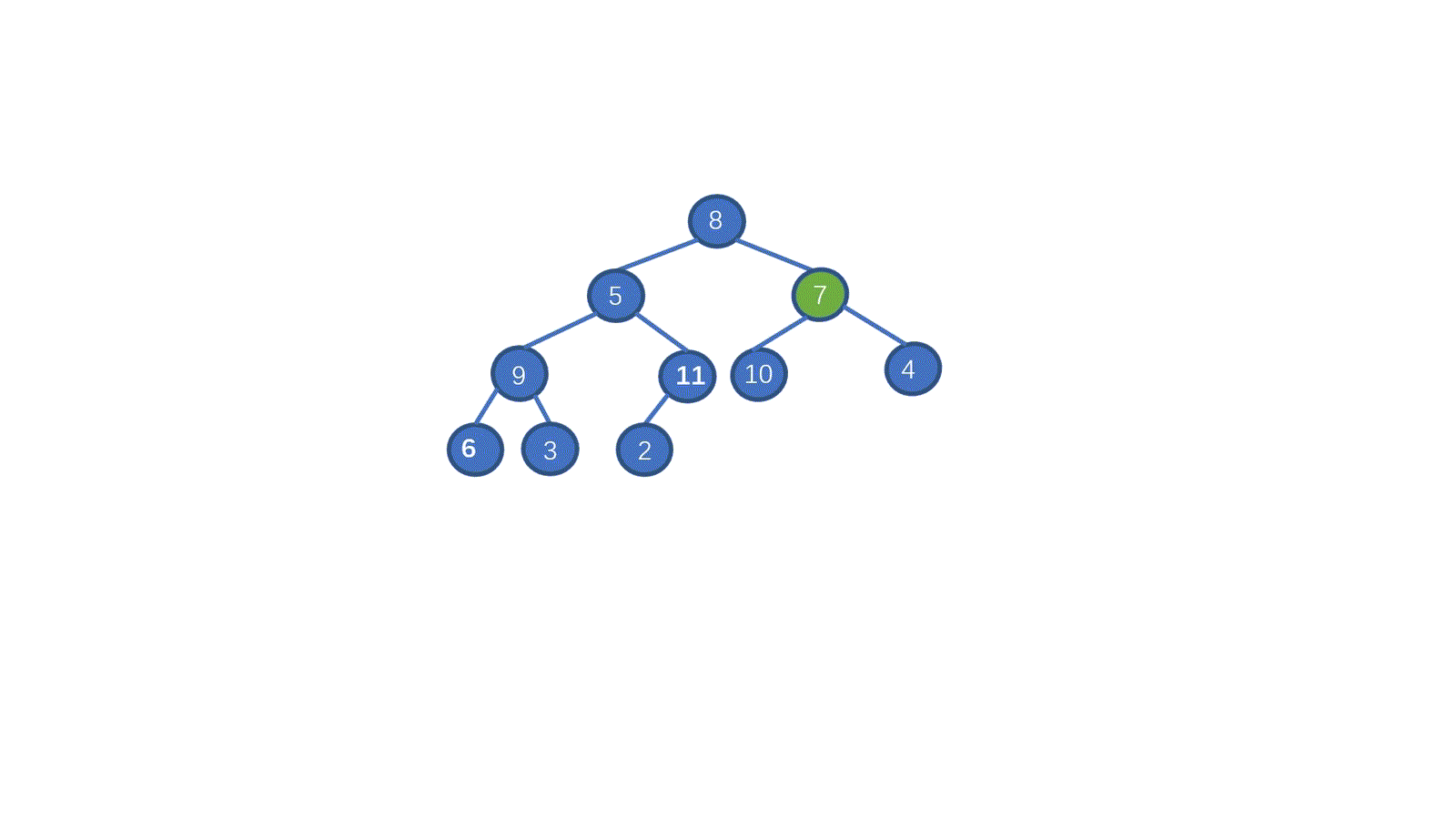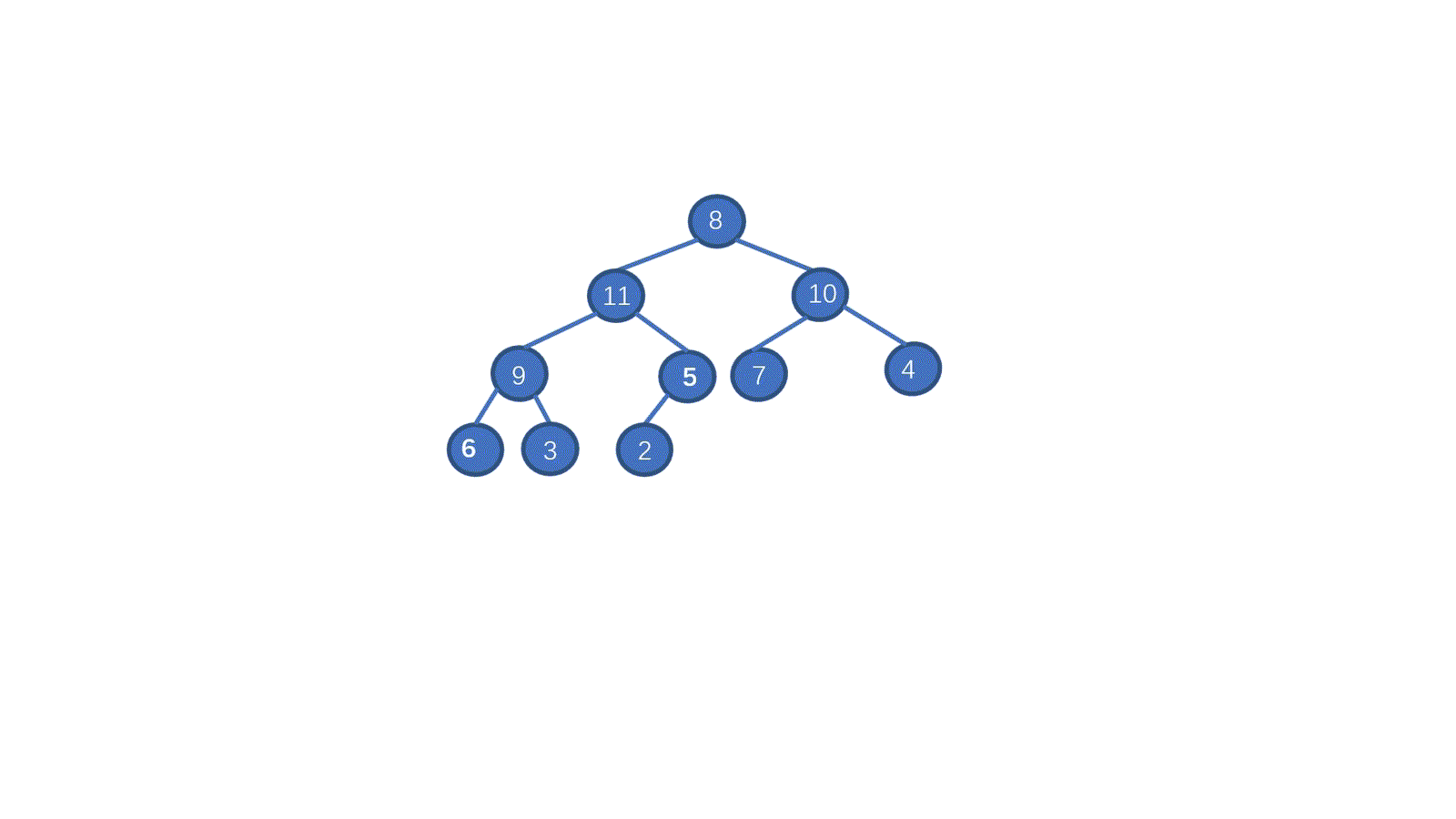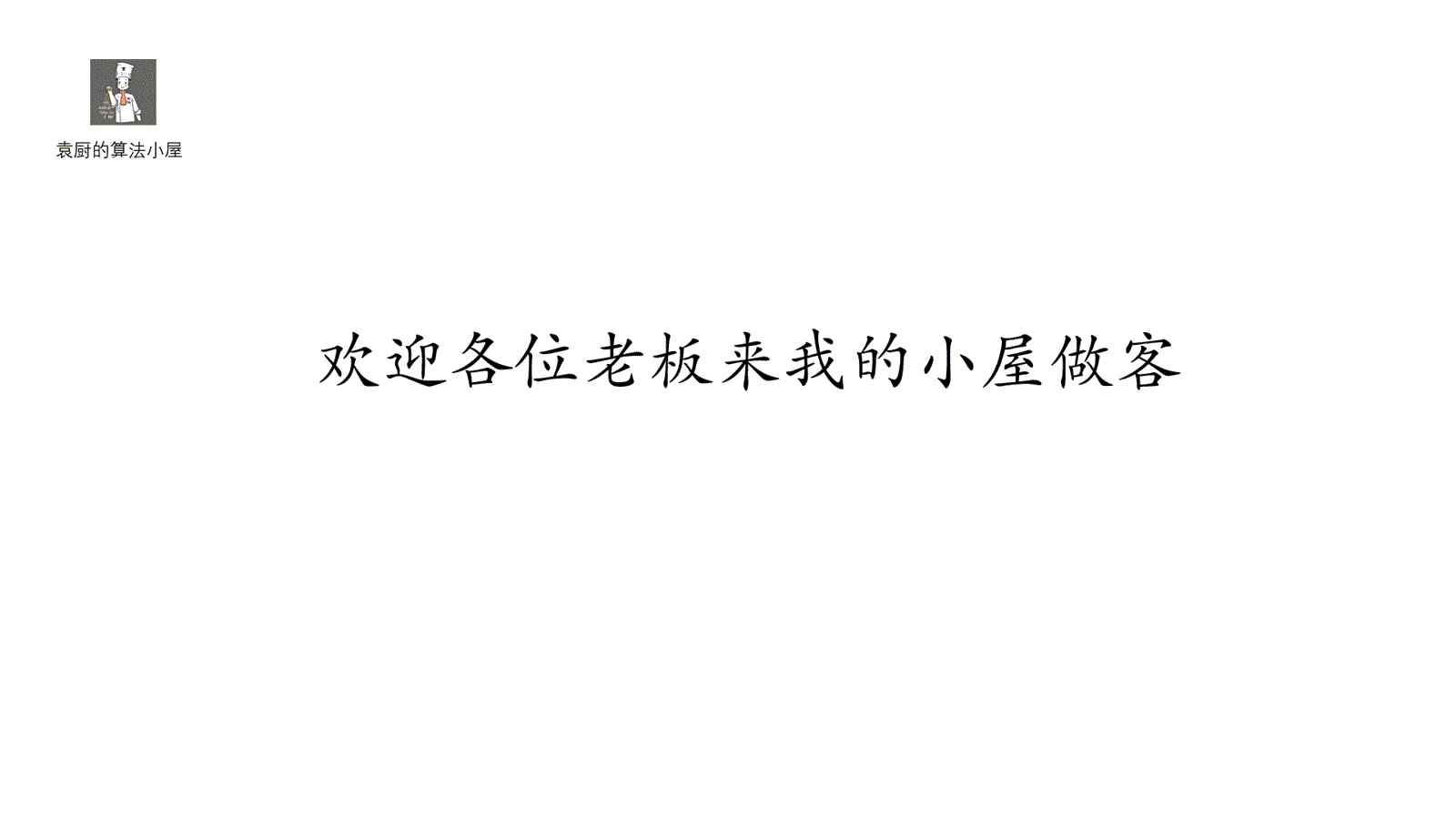
|
|
||||||
|
|
||||||
我们一起来拆解一下视频,我们只需要从最后一个非叶子节点开始,依次执行下沉操作。执行完毕后我们就能够完成堆化。是不是一下就懂了呀。
|
|
||||||
|
|
||||||
好啦我们一起看哈下沉操作的代码吧。
|
|
||||||
|
|
||||||
```java
|
|
||||||
public void sink (int[] nums, int index,int len) {
|
|
||||||
while (true) {
|
|
||||||
//获取子节点
|
|
||||||
int j = 2 * index;
|
|
||||||
if (j < len-1 && nums[j] < nums[j+1]) {
|
|
||||||
j++;
|
|
||||||
}
|
|
||||||
//交换操作,父节点下沉,与最大的孩子节点交换
|
|
||||||
if (j < len && nums[index] < nums[j]) {
|
|
||||||
swap(nums,index,j);
|
|
||||||
} else {
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
//继续下沉
|
|
||||||
index = j;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
好啦,两种建堆方式我们都已经了解啦,那么我们如何进行排序呢?
|
|
||||||
|
|
||||||
了解排序之前我们先来,看一下如何删除堆顶元素,我们需要保证的是,删除堆顶元素后,其他元素仍能满足堆的要求,我们思考一下如何实现呢?见下图
|
|
||||||
|
|
||||||
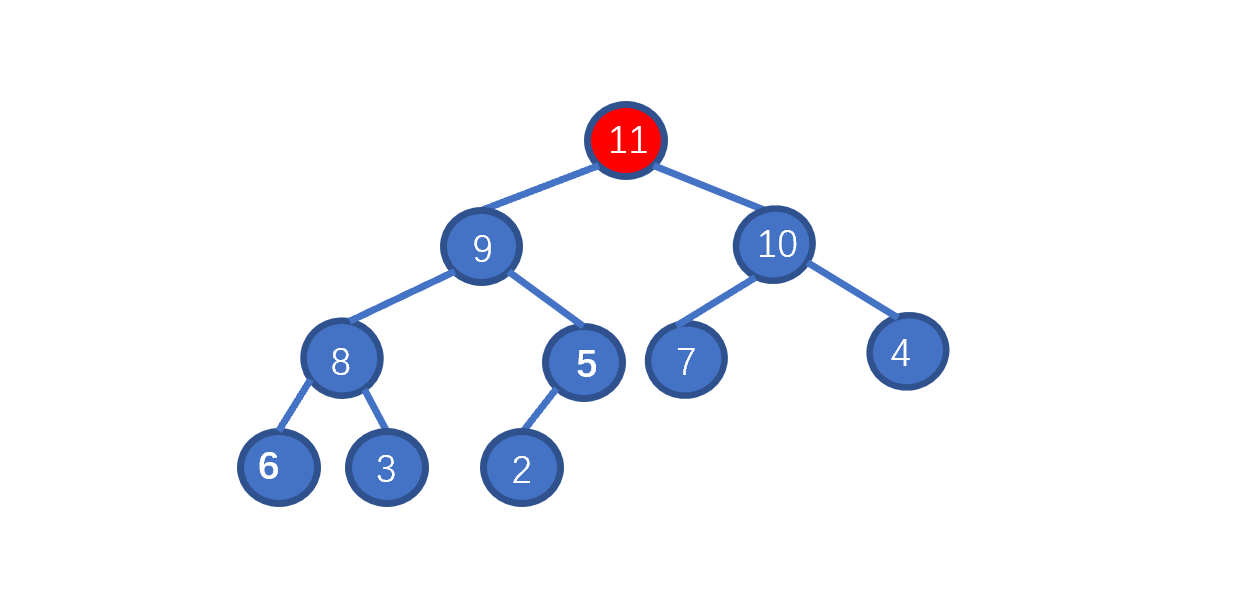
|
|
||||||
|
|
||||||
假设我们想要去除堆顶的 11 ,那我们则需要将其与堆的最后一个节点交换也就是 2 ,2然后再执行下沉操作,执行完毕后仍能满足堆的要求,见下图
|
|
||||||
|
|
||||||
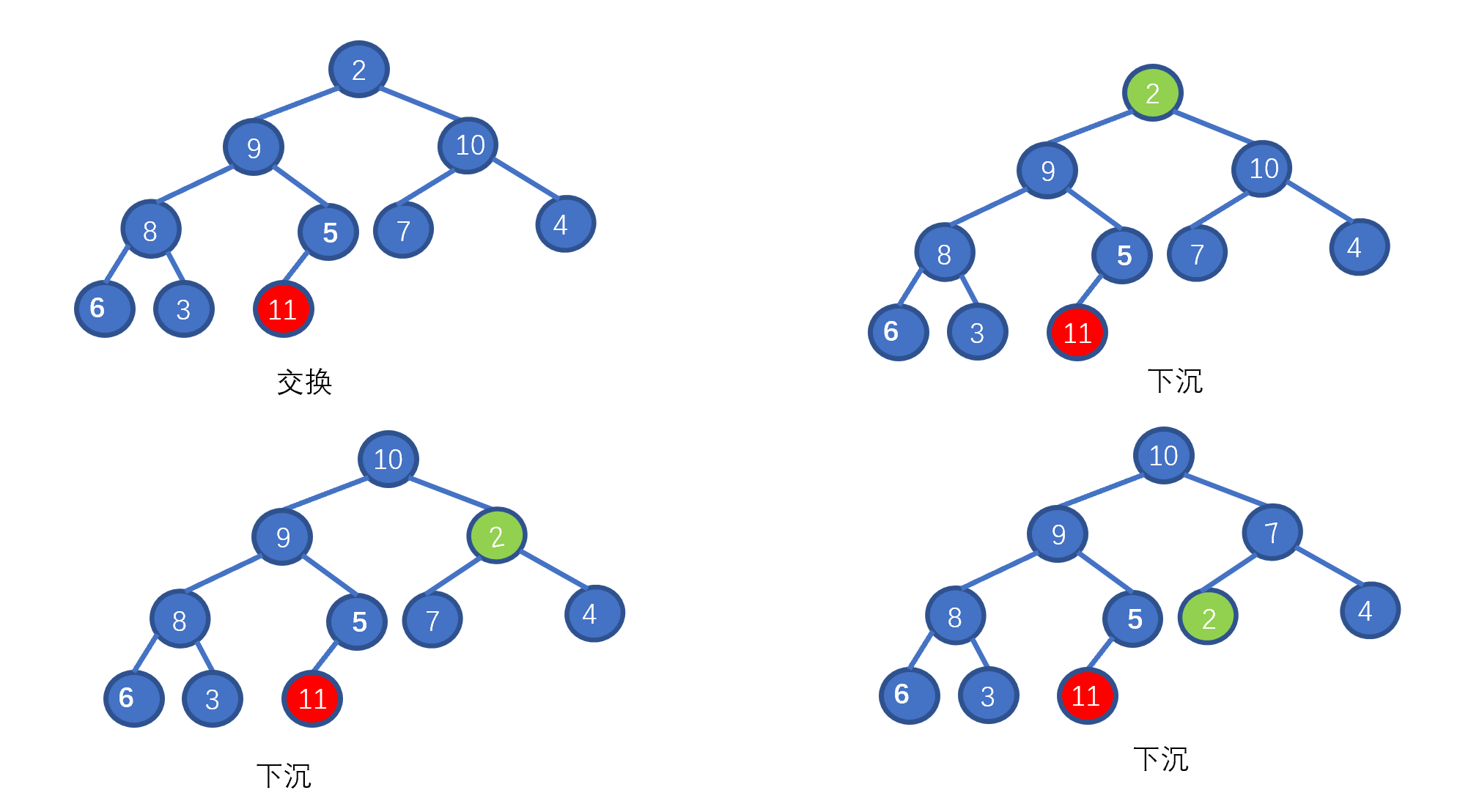
|
|
||||||
|
|
||||||
好啦,其实你已经学会如何排序啦!你不信?那我给你放视频
|
|
||||||
|
|
||||||
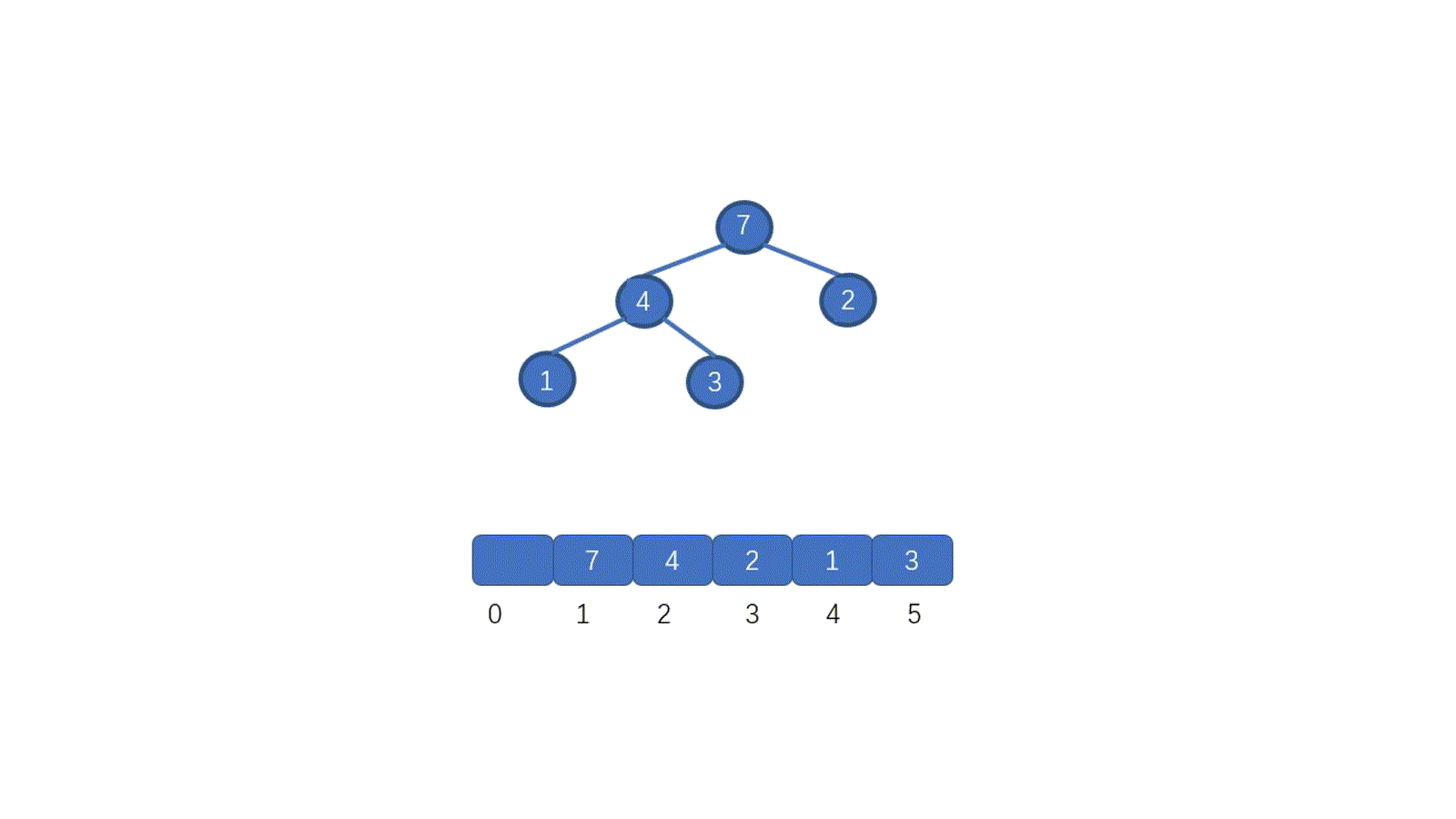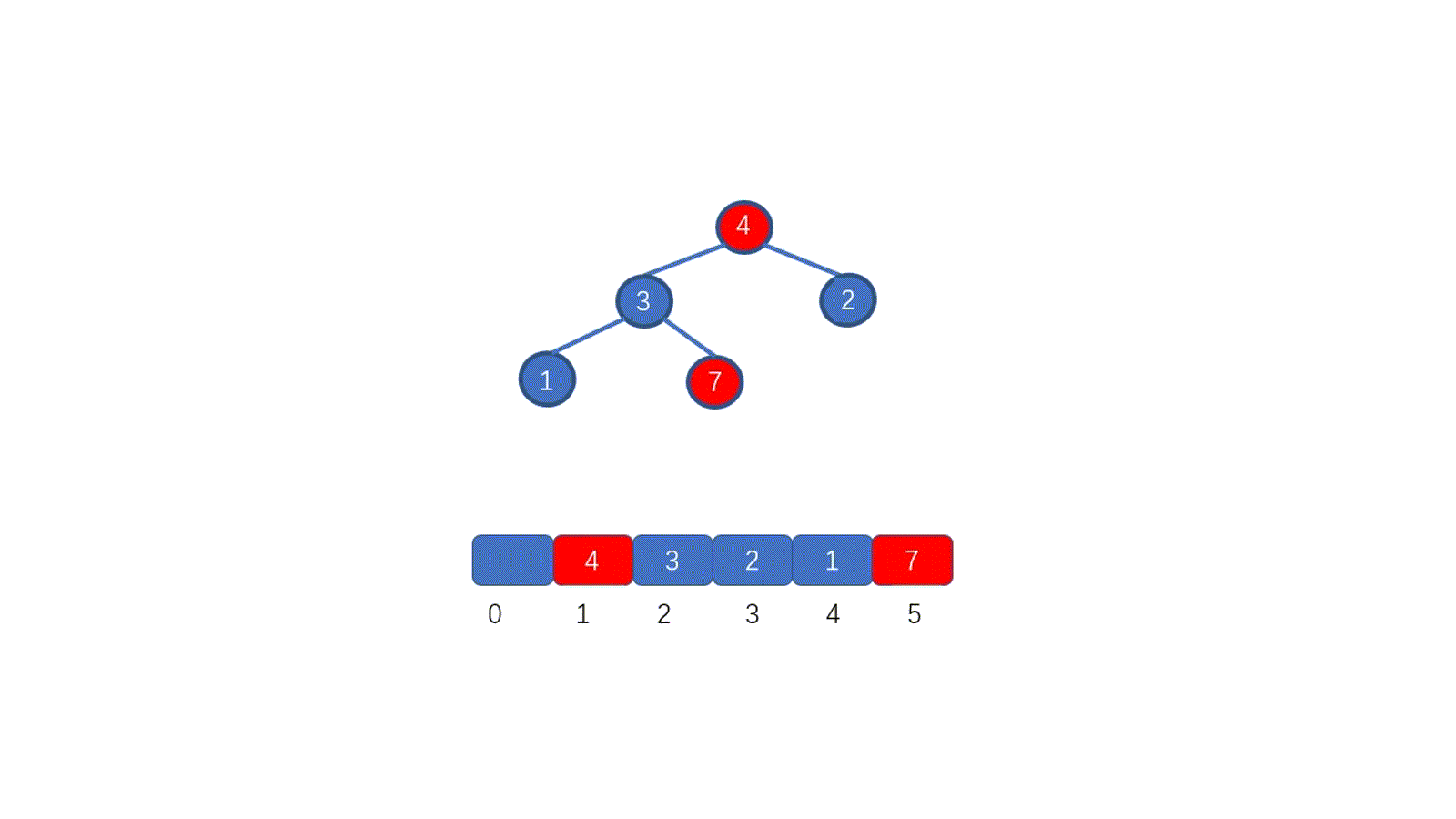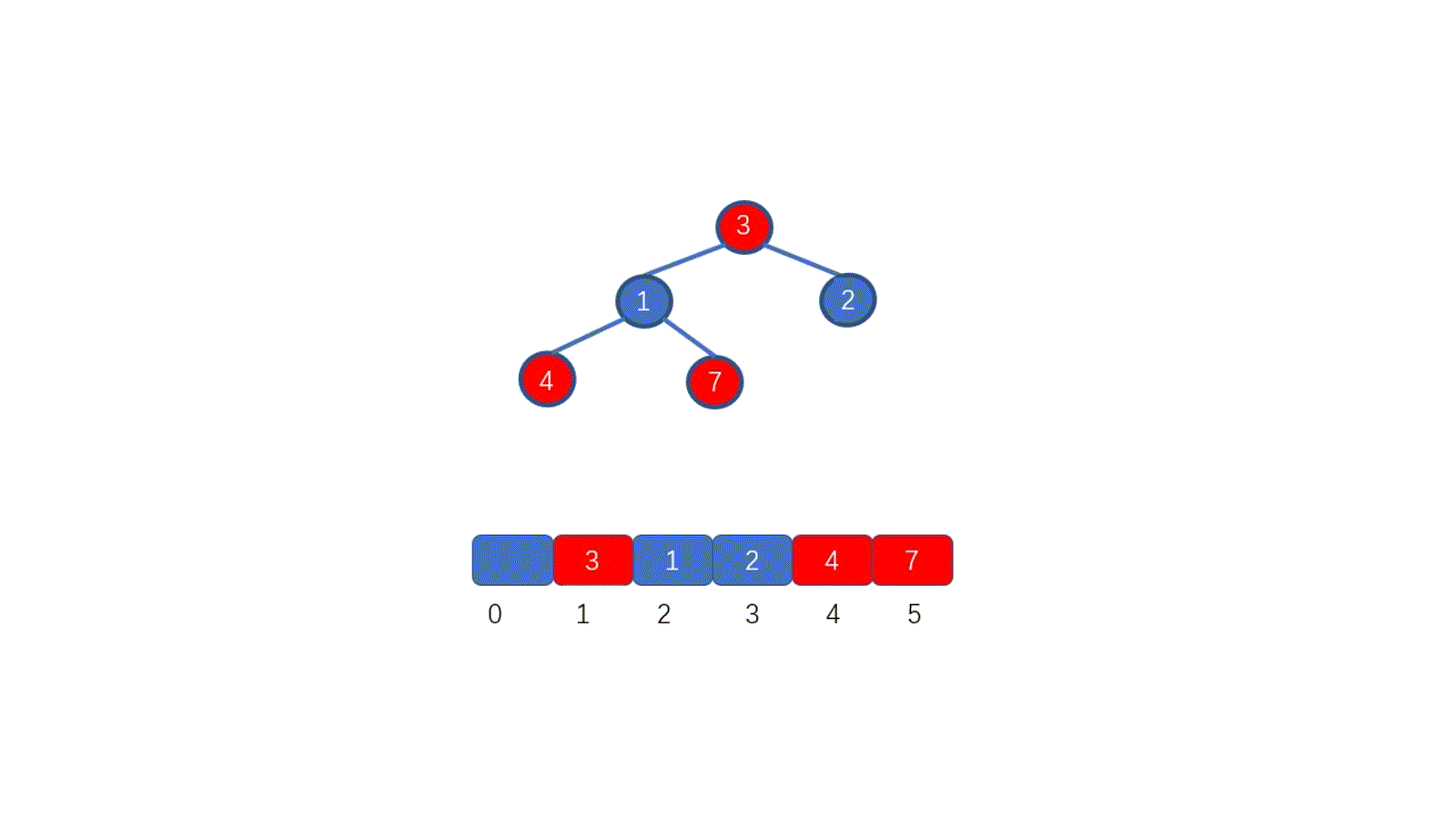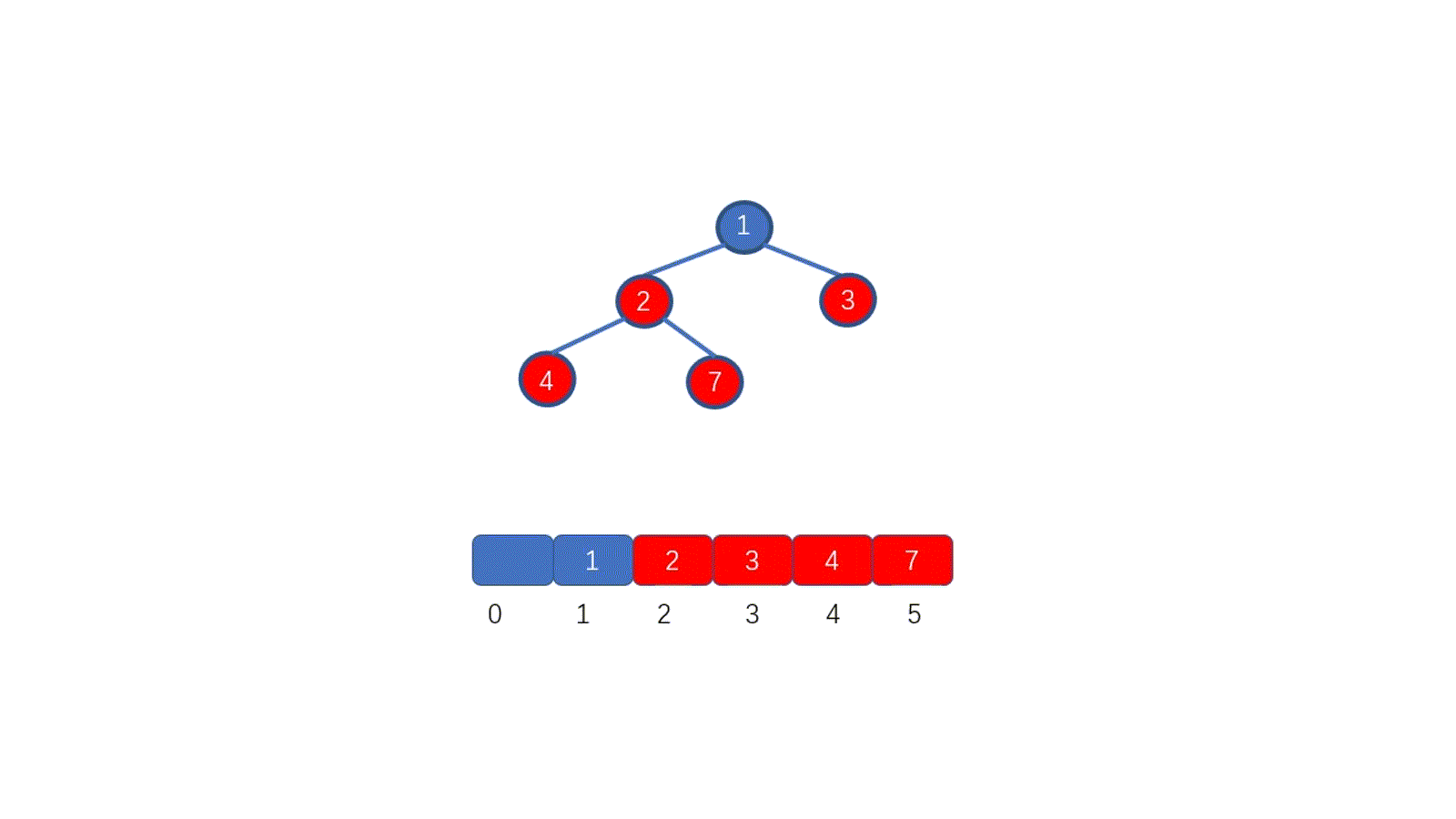
|
|
||||||
|
|
||||||
好啦,大家是不是已经搞懂啦,下面我们总结一下堆排序的具体执行过程
|
|
||||||
|
|
||||||
1.建堆,通过下沉操作建堆效率更高,具体过程是,找到最后一个非叶子节点,然后从后往前遍历执行下沉操作。
|
|
||||||
|
|
||||||
2.排序,将堆顶元素(代表最大元素)与最后一个元素交换,然后新的堆顶元素进行下沉操作,遍历执行上诉操作,则可以完成排序。
|
|
||||||
|
|
||||||
好啦,下面我们一起看代码吧
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
|
|
||||||
int len = nums.length;
|
|
||||||
int[] a = new int[len + 1];
|
|
||||||
|
|
||||||
for (int i = 0; i < nums.length; ++i) {
|
|
||||||
a[i+1] = nums[i];
|
|
||||||
}
|
|
||||||
//下沉建堆
|
|
||||||
for (int i = len/2; i >= 1; --i) {
|
|
||||||
sink(a,i,len);
|
|
||||||
}
|
|
||||||
|
|
||||||
int k = len;
|
|
||||||
//排序
|
|
||||||
while (k > 1) {
|
|
||||||
swap(a,1,k--);
|
|
||||||
sink(a,1,k);
|
|
||||||
}
|
|
||||||
for (int i = 1; i < len+1; ++i) {
|
|
||||||
nums[i-1] = a[i];
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
public void sink (int[] nums, int k,int end) {
|
|
||||||
//下沉
|
|
||||||
while (2 * k <= end) {
|
|
||||||
int j = 2 * k;
|
|
||||||
//找出子节点中最大或最小的那个
|
|
||||||
if (j + 1 <= end && nums[j + 1] > nums[j]) {
|
|
||||||
j++;
|
|
||||||
}
|
|
||||||
if (nums[j] > nums[k]) {
|
|
||||||
swap(nums, j, k);
|
|
||||||
} else {
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
k = j;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
public void swap (int nums[], int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
好啦,堆排序我们就到这里啦,是不是搞定啦,总的来说堆排序比其他排序算法稍微难理解一些,重点就是建堆,而且应用比较广泛,大家记得打卡呀。
|
|
||||||
|
|
||||||
好啦,我们再来分析一下堆排序的时间复杂度、空间复杂度以及稳定性。
|
|
||||||
|
|
||||||
**堆排序时间复杂度分析**
|
|
||||||
|
|
||||||
因为我们建堆的时间复杂度为 O(n),排序过程的时间复杂度为 O(nlogn),所以总的空间复杂度为 O(nlogn)
|
|
||||||
|
|
||||||
**堆排序空间复杂度分析**
|
|
||||||
|
|
||||||
这里需要注意,我们上面的描述过程中,为了更直观的描述,空出数组的第一位,这样我们就可以通过 i * 2 和 i * 2+1 来求得左孩子节点和右孩子节点 。我们也可以根据 i * 2 + 1 和 i * 2 + 2 来获取孩子节点,这样则不需要临时数组来处理原数组,将所有元素后移一位,所以堆排序的空间复杂度为 O(1),是原地排序算法。
|
|
||||||
|
|
||||||
**堆排序稳定性分析**
|
|
||||||
|
|
||||||
堆排序不是稳定的排序算法,在排序的过程,我们会将堆的最后一个节点跟堆顶节点交换,改变相同元素的原始相对位置。
|
|
||||||
|
|
||||||
最后我们来比较一下我们快速排序和堆排序
|
|
||||||
|
|
||||||
1.对于快速排序来说,数据是顺序访问的。而对于堆排序来说,数据是跳着访问的。这样对 CPU 缓存是不友好的
|
|
||||||
|
|
||||||
2.相同的的数据,排序过程中,堆排序的数据交换次数要多于快速排序。
|
|
||||||
|
|
||||||
所以上面两条也就说明了在实际开发中,堆排序的性能不如快速排序性能好。
|
|
||||||
|
|
||||||
好啦,今天的内容就到这里啦,咱们下期见。
|
|
||||||
@ -1,486 +0,0 @@
|
|||||||
|
|
||||||
|
|
||||||
> 为保证代码严谨性,文中所有代码均在 leetcode 刷题网站 AC ,大家可以放心食用。
|
|
||||||
|
|
||||||
皇上生辰之际,举国同庆,袁记菜馆作为天下第一饭店,所以被选为这次庆典的菜品供应方,这次庆典对于袁记菜馆是一项前所未有的挑战,毕竟是第一次给皇上庆祝生辰,稍有不慎就是掉脑袋的大罪,整个袁记菜馆内都在紧张的布置着。此时突然有一个店小二慌慌张张跑到袁厨面前汇报,到底发生了什么事,让店小二如此慌张呢?
|
|
||||||
|
|
||||||
袁记菜馆内
|
|
||||||
|
|
||||||
店小二:不好了不好了,掌柜的,出大事了。
|
|
||||||
|
|
||||||
袁厨:发生什么事了,慢慢说,如此慌张,成何体统。(开店开久了,架子出来了哈)
|
|
||||||
|
|
||||||
店小二:皇上按照咱们菜单点了 666 道菜,但是咱们做西湖醋鱼的师傅请假回家结婚了,不知道皇上有没有点这道菜,如果点了这道菜,咱们做不出来,那咱们店可就完了啊。
|
|
||||||
|
|
||||||
(袁厨听了之后,吓得一屁股坐地上了,缓了半天说道)
|
|
||||||
|
|
||||||
袁厨:别说那么多了,快给我找找皇上点的菜里面,有没有这道菜!
|
|
||||||
|
|
||||||
找了很久,并且核对了很多遍,最后确认皇上没有点这道菜。菜馆内的人都松了一口气
|
|
||||||
|
|
||||||
通过上面的一个例子,让我们简单了解了字符串匹配。
|
|
||||||
|
|
||||||
字符串匹配:设 S 和 T 是给定的两个串,在主串 S 中找到模式串 T 的过程称为字符串匹配,如果在主串 S 中找到 模式串 T ,则称匹配成功,函数返回 T 在 S 中首次出现的位置,否则匹配不成功,返回 -1。
|
|
||||||
|
|
||||||
例:
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
在上图中,我们试图找到模式 T = baab,在主串 S = abcabaabcabac 中第一次出现的位置,即为红色阴影部分, T 第一次在 S 中出现的位置下标为 4 ( 字符串的首位下标是 0 ),所以返回 4。如果模式串 T 没有在主串 S 中出现,则返回 -1。
|
|
||||||
|
|
||||||
解决上面问题的算法我们称之为字符串匹配算法,今天我们来介绍三种字符串匹配算法,大家记得打卡呀,说不准面试的时候就问到啦。
|
|
||||||
|
|
||||||
## BF算法(Brute Force)
|
|
||||||
|
|
||||||
这个算法很容易理解,就是我们将模式串和主串进行比较,一致时则继续比较下一字符,直到比较完整个模式串。不一致时则将模式串后移一位,重新从模式串的首位开始对比,重复刚才的步骤下面我们看下这个方法的动图解析,看完肯定一下就能搞懂啦。
|
|
||||||
|
|
||||||
视频详解
|
|
||||||
|
|
||||||
**因为不可以放置视频,所以想看视频的同学,可以去看公众号原文,那里有视频**
|
|
||||||
|
|
||||||
通过上面的代码是不是一下就将这个算法搞懂啦,下面我们用这个算法来解决下面这个经典题目吧。
|
|
||||||
|
|
||||||
### leetcdoe 28. 实现 strStr()
|
|
||||||
|
|
||||||
#### 题目描述
|
|
||||||
|
|
||||||
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
|
|
||||||
|
|
||||||
示例 1:
|
|
||||||
|
|
||||||
> 输入: haystack = "hello", needle = "ll"
|
|
||||||
> 输出: 2
|
|
||||||
|
|
||||||
示例 2:
|
|
||||||
|
|
||||||
> 输入: haystack = "aaaaa", needle = "bba"
|
|
||||||
> 输出: -1
|
|
||||||
|
|
||||||
#### 题目解析
|
|
||||||
|
|
||||||
其实这个题目很容易理解,但是我们需要注意的是一下几点,比如我们的模式串为 0 时,应该返回什么,我们的模式串长度大于主串长度时,应该返回什么,也是我们需要注意的地方。下面我们来看一下题目代码吧。
|
|
||||||
|
|
||||||
#### 题目代码
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
int haylen = haystack.length();
|
|
||||||
int needlen = needle.length();
|
|
||||||
//特殊情况
|
|
||||||
if (haylen < needlen) {
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
if (needlen == 0) {
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
//主串
|
|
||||||
for (int i = 0; i < haylen - needlen + 1; ++i) {
|
|
||||||
int j;
|
|
||||||
//模式串
|
|
||||||
for (j = 0; j < needlen; j++) {
|
|
||||||
//不符合的情况,直接跳出,主串指针后移一位
|
|
||||||
if (haystack.charAt(i+j) != needle.charAt(j)) {
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//匹配成功
|
|
||||||
if (j == needlen) {
|
|
||||||
return i;
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们看一下BF算法的另一种算法(显示回退),其实原理一样,就是对代码进行了一下修改,只要是看完咱们的动图,这个也能够一下就能看懂,大家可以结合下面代码中的注释和动图进行理解。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
//i代表主串指针,j模式串
|
|
||||||
int i,j;
|
|
||||||
//主串长度和模式串长度
|
|
||||||
int halen = haystack.length();
|
|
||||||
int nelen = needle.length();
|
|
||||||
//循环条件,这里只有 i 增长
|
|
||||||
for (i = 0 , j = 0; i < halen && j < nelen; ++i) {
|
|
||||||
//相同时,则移动 j 指针
|
|
||||||
if (haystack.charAt(i) == needle.charAt(j)) {
|
|
||||||
++j;
|
|
||||||
} else {
|
|
||||||
//不匹配时,将 j 重新指向模式串的头部,将 i 本次匹配的开始位置的下一字符
|
|
||||||
i -= j;
|
|
||||||
j = 0;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//查询成功时返回索引,查询失败时返回 -1;
|
|
||||||
int renum = j == nelen ? i - nelen : -1;
|
|
||||||
return renum;
|
|
||||||
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## BM算法(Boyer-Moore)
|
|
||||||
|
|
||||||
我们刚才说过了 BF 算法,但是 BF 算法是有缺陷的,比如我们下面这种情况
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如上图所示,如果我们利用 BF 算法,遇到不匹配字符时,每次右移一位模式串,再重新从头进行匹配,我们观察一下,我们的模式串 abcdex 中每个字符都不一样,但是我们第一次进行字符串匹配时,abcde 都匹配成功,到 x 时失败,又因为模式串每位都不相同,所以我们不需要再每次右移一位,再重新比较,我们可以直接跳过某些步骤。如下图
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们可以跳过其中某些步骤,直接到下面这个步骤。那我们是依据什么原则呢?
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
### 坏字符规则
|
|
||||||
|
|
||||||
我们之前的 BF 算法是从前往后进行比较 ,BM 算法是从后往前进行比较,我们来看一下具体过程,我们还是利用上面的例子。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
BM 算法是从后往前进行比较,此时我们发现比较的第一个字符就不匹配,我们将**主串**这个字符称之为**坏字符**,也就是 f ,我们发现坏字符之后,模式串 T 中查找是否含有该字符(f),我们发现并不存在 f,此时我们只需将模式串右移到坏字符的后面一位即可。如下图
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
那我们在模式串中找到坏字符该怎么办呢?
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
此时我们的坏字符为 f ,我们在模式串中,查找发现含有坏字符 f,我们则需要移动模式串 T ,将模式串中的 f 和坏字符对齐。见下图。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
然后我们继续从右往左进行比较,发现 d 为坏字符,则需要将模式串中的 d 和坏字符对齐。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
那么我们在来思考一下这种情况,那就是模式串中含有多个坏字符怎么办呢?
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
那么我们为什么要让**最靠右的对应元素与坏字符匹配**呢?如果上面的例子我们没有按照这条规则看下会产生什么问题。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
如果没有按照我们上述规则,则会**漏掉我们的真正匹配**。我们的主串中是**含有 babac** 的,但是却**没有匹配成功**,所以应该遵守**最靠右的对应字符与坏字符相对**的规则。
|
|
||||||
|
|
||||||
我们上面一共介绍了三种移动情况,分别是下方的模式串中没有发现与坏字符对应的字符,发现一个对应字符,发现两个。这三种情况我们分别移动不同的位数,那我们是根据依据什么来决定移动位数的呢?下面我们给图中的字符加上下标。见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
下面我们来考虑一下这种情况。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
此时这种情况肯定是不行的,不往右移动,甚至还有可能左移,那么我们有没有什么办法解决这个问题呢?继续往下看吧。
|
|
||||||
|
|
||||||
### 好后缀规则
|
|
||||||
|
|
||||||
好后缀其实也很容易理解,我们之前说过 BM 算法是从右往左进行比较,下面我们来看下面这个例子。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
这里如果我们按照坏字符进行移动是不合理的,这时我们可以使用好后缀规则,那么什么是好后缀呢?
|
|
||||||
|
|
||||||
BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已经匹配成功,在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀,此时我们拿它在模式串中查找,如果找到了另一个和好后缀相匹配的串,那我们就将另一个和**好后缀相匹配**的串 ,滑到和好后缀对齐的位置。
|
|
||||||
|
|
||||||
是不是感觉有点拗口,没关系,我们看下图,红色代表坏字符,绿色代表好后缀
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
上面那种情况搞懂了,但是我们思考一下下面这种情况
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
上面我们说到了,如果在模式串的**头部**没有发现好后缀,发现好后缀的子串也可以。但是为什么要强调这个头部呢?
|
|
||||||
|
|
||||||
我们下面来看一下这种情况
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
但是当我们在头部发现好后缀的子串时,是什么情况呢?
|
|
||||||
|
|
||||||
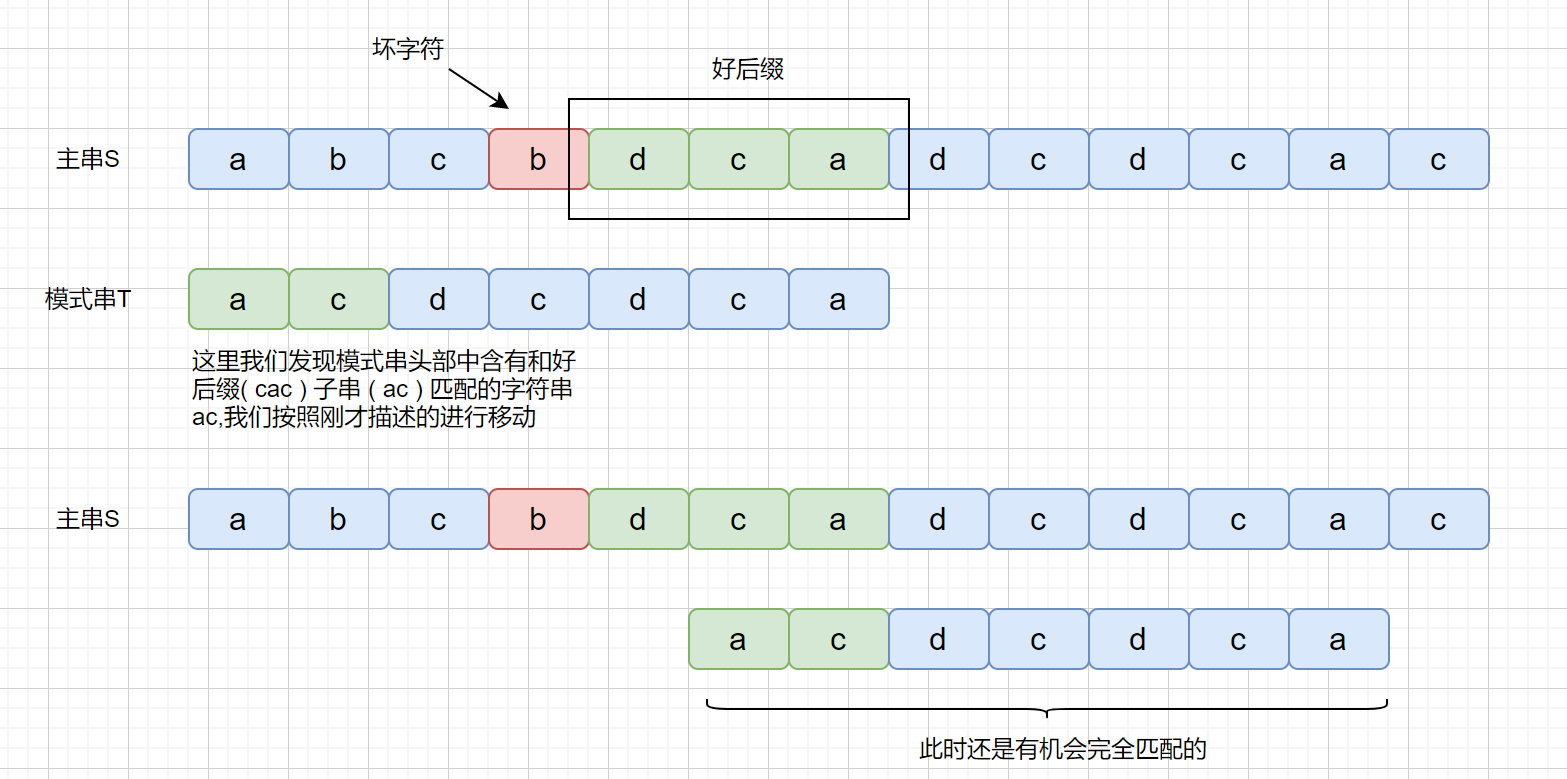
|
|
||||||
|
|
||||||
下面我们通过动图来看一下某一例子的具体的执行过程
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
视频
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
说到这里,坏字符和好后缀规则就算说完了,坏字符很容易理解,我们对好后缀总结一下
|
|
||||||
|
|
||||||
1.如果模式串**含有好后缀**,无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次,则以**最右侧的好后缀**为基准。
|
|
||||||
|
|
||||||
2.如果模式串**头部含有**好后缀子串则可以按照规则进行移动,中间部分含有好后缀子串则不可以。
|
|
||||||
|
|
||||||
3.如果在模式串尾部就出现不匹配的情况,即不存在好后缀时,则根据坏字符进行移动,这里有的文章没有提到,是个需要特别注意的地方,我是在这个论文里找到答案的,感兴趣的同学可以看下。
|
|
||||||
|
|
||||||
> Boyer R S,Moore J S. A fast string searching algorithm[J]. Communications of the ACM,1977,10: 762-772.
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
之前我们刚开始说坏字符的时候,是不是有可能会出现负值的情况,即往左移动的情况,所以我们为了解决这个问题,我们可以分别计算好后缀和坏字符往后滑动的位数**(好后缀不为 0 的情况)**,然后取两个数中最大的,作为模式串往后滑动的位数。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
这破图画起来是真费劲啊。下面我们来看一下算法代码,代码有点长,我都标上了注释也在网站上 AC 了,如果各位感兴趣可以看一下,不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
char[] hay = haystack.toCharArray();
|
|
||||||
char[] need = needle.toCharArray();
|
|
||||||
int haylen = haystack.length();
|
|
||||||
int needlen = need.length;
|
|
||||||
return bm(hay,haylen,need,needlen);
|
|
||||||
}
|
|
||||||
//用来求坏字符情况下移动位数
|
|
||||||
private static void badChar(char[] b, int m, int[] bc) {
|
|
||||||
//初始化
|
|
||||||
for (int i = 0; i < 256; ++i) {
|
|
||||||
bc[i] = -1;
|
|
||||||
}
|
|
||||||
//m 代表模式串的长度,如果有两个 a,则后面那个会覆盖前面那个
|
|
||||||
for (int i = 0; i < m; ++i) {
|
|
||||||
int ascii = (int)b[i];
|
|
||||||
bc[ascii] = i;//下标
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//用来求好后缀条件下的移动位数
|
|
||||||
private static void goodSuffix (char[] b, int m, int[] suffix,boolean[] prefix) {
|
|
||||||
//初始化
|
|
||||||
for (int i = 0; i < m; ++i) {
|
|
||||||
suffix[i] = -1;
|
|
||||||
prefix[i] = false;
|
|
||||||
}
|
|
||||||
for (int i = 0; i < m - 1; ++i) {
|
|
||||||
int j = i;
|
|
||||||
int k = 0;
|
|
||||||
while (j >= 0 && b[j] == b[m-1-k]) {
|
|
||||||
--j;
|
|
||||||
++k;
|
|
||||||
suffix[k] = j + 1;
|
|
||||||
}
|
|
||||||
if (j == -1) prefix[k] = true;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
public static int bm (char[] a, int n, char[] b, int m) {
|
|
||||||
|
|
||||||
int[] bc = new int[256];//创建一个数组用来保存最右边字符的下标
|
|
||||||
badChar(b,m,bc);
|
|
||||||
//用来保存各种长度好后缀的最右位置的数组
|
|
||||||
int[] suffix_index = new int[m];
|
|
||||||
//判断是否是头部,如果是头部则true
|
|
||||||
boolean[] ispre = new boolean[m];
|
|
||||||
goodSuffix(b,m,suffix_index,ispre);
|
|
||||||
int i = 0;//第一个匹配字符
|
|
||||||
//注意结束条件
|
|
||||||
while (i <= n-m) {
|
|
||||||
int j;
|
|
||||||
//从后往前匹配,匹配失败,找到坏字符
|
|
||||||
for (j = m - 1; j >= 0; --j) {
|
|
||||||
if (a[i+j] != b[j]) break;
|
|
||||||
}
|
|
||||||
//模式串遍历完毕,匹配成功
|
|
||||||
if (j < 0) {
|
|
||||||
return i;
|
|
||||||
}
|
|
||||||
//下面为匹配失败时,如何处理
|
|
||||||
//求出坏字符规则下移动的位数,就是我们坏字符下标减最右边的下标
|
|
||||||
int x = j - bc[(int)a[i+j]];
|
|
||||||
int y = 0;
|
|
||||||
//好后缀情况,求出好后缀情况下的移动位数,如果不含有好后缀的话,则按照坏字符来
|
|
||||||
if (y < m-1 && m - 1 - j > 0) {
|
|
||||||
y = move(j, m, suffix_index,ispre);
|
|
||||||
}
|
|
||||||
//移动
|
|
||||||
i = i + Math.max(x,y);
|
|
||||||
|
|
||||||
}
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
// j代表坏字符的下标
|
|
||||||
private static int move (int j, int m, int[] suffix_index, boolean[] ispre) {
|
|
||||||
//好后缀长度
|
|
||||||
int k = m - 1 - j;
|
|
||||||
//如果含有长度为 k 的好后缀,返回移动位数,
|
|
||||||
if (suffix_index[k] != -1) return j - suffix_index[k] + 1;
|
|
||||||
//找头部为好后缀子串的最大长度,从长度最大的子串开始
|
|
||||||
for (int r = j + 2; r <= m-1; ++r) {
|
|
||||||
//如果是头部
|
|
||||||
if (ispre[m-r] == true) {
|
|
||||||
return r;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//如果没有发现好后缀匹配的串,或者头部为好后缀子串,则移动到 m 位,也就是匹配串的长度
|
|
||||||
return m;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
我们来理解一下我们代码中用到的两个数组,因为两个规则的移动位数,只与模式串有关,与主串无关,所以我们可以提前求出每种情况的移动情况,保存到数组中。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
## KMP算法(Knuth-Morris-Pratt)
|
|
||||||
|
|
||||||
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
|
|
||||||
|
|
||||||
我们先来看一个实例
|
|
||||||
|
|
||||||
视频
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
|
|
||||||
|
|
||||||
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
|
|
||||||
|
|
||||||
在上面的例子中我们提到了一个名词,**最长公共前后缀**,这个是什么意思呢?下面我们通过一个较简单的例子进行描述。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
此时我们在红色阴影处匹配失败,绿色为匹配成功部分,则我们观察匹配成功的部分。
|
|
||||||
|
|
||||||
我们来看一下匹配成功部分的所有前缀
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们的最长公共前后缀如下图,则我们需要这样移动
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
|
||||||
|
|
||||||
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
|
|
||||||
|
|
||||||
next 数组存的咱们最长公共前后缀中,前缀的结尾字符下标。是不是感觉有点别扭,我们通过一个例子进行说明。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们知道 next 数组之后,我们的 KMP 算法实现起来就很容易啦,另外我们看一下 next 数组到底是干什么用的。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
剩下的就不用说啦,完全一致啦,咱们将上面这个例子,翻译成和咱们开头对应的动画大家看一下。
|
|
||||||
|
|
||||||
**因为不可以放置视频,所以想看视频的同学,可以去看公众号原文,那里有视频**
|
|
||||||
|
|
||||||
下面我们看一下代码,标有详细注释,大家认真看呀。
|
|
||||||
|
|
||||||
**注:很多教科书的 next 数组表示方式不一致,理解即可**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int strStr(String haystack, String needle) {
|
|
||||||
//两种特殊情况
|
|
||||||
if (needle.length() == 0) {
|
|
||||||
return 0;
|
|
||||||
}
|
|
||||||
if (haystack.length() == 0) {
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
// char 数组
|
|
||||||
char[] hasyarr = haystack.toCharArray();
|
|
||||||
char[] nearr = needle.toCharArray();
|
|
||||||
//长度
|
|
||||||
int halen = hasyarr.length;
|
|
||||||
int nelen = nearr.length;
|
|
||||||
//返回下标
|
|
||||||
return kmp(hasyarr,halen,nearr,nelen);
|
|
||||||
|
|
||||||
}
|
|
||||||
public int kmp (char[] hasyarr, int halen, char[] nearr, int nelen) {
|
|
||||||
//获取next 数组
|
|
||||||
int[] next = next(nearr,nelen);
|
|
||||||
int j = 0;
|
|
||||||
for (int i = 0; i < halen; ++i) {
|
|
||||||
//发现不匹配的字符,然后根据 next 数组移动指针,移动到最大公共前后缀的,
|
|
||||||
//前缀的后一位,和咱们移动模式串的含义相同
|
|
||||||
while (j > 0 && hasyarr[i] != nearr[j]) {
|
|
||||||
j = next[j - 1] + 1;
|
|
||||||
//超出长度时,可以直接返回不存在
|
|
||||||
if (nelen - j + i > halen) {
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//如果相同就将指针同时后移一下,比较下个字符
|
|
||||||
if (hasyarr[i] == nearr[j]) {
|
|
||||||
++j;
|
|
||||||
}
|
|
||||||
//遍历完整个模式串,返回模式串的起点下标
|
|
||||||
if (j == nelen) {
|
|
||||||
return i - nelen + 1;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return -1;
|
|
||||||
}
|
|
||||||
//这一块比较难懂,不想看的同学可以忽略,了解大致含义即可,或者自己调试一下,看看运行情况
|
|
||||||
//我会每一步都写上注释
|
|
||||||
public int[] next (char[] needle,int len) {
|
|
||||||
//定义 next 数组
|
|
||||||
int[] next = new int[len];
|
|
||||||
// 初始化
|
|
||||||
next[0] = -1;
|
|
||||||
int k = -1;
|
|
||||||
for (int i = 1; i < len; ++i) {
|
|
||||||
//我们此时知道了 [0,i-1]的最长前后缀,但是k+1的指向的值和i不相同时,我们则需要回溯
|
|
||||||
//因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标(即长度)
|
|
||||||
//就要找 k+1前一个元素在next数组里的值,即next[k+1]
|
|
||||||
while (k != -1 && needle[k + 1] != needle[i]) {
|
|
||||||
k = next[k];
|
|
||||||
}
|
|
||||||
// 相同情况,就是 k的下一位,和 i 相同时,此时我们已经知道 [0,i-1]的最长前后缀
|
|
||||||
//然后 k - 1 又和 i 相同,最长前后缀加1,即可
|
|
||||||
if (needle[k+1] == needle[i]) {
|
|
||||||
++k;
|
|
||||||
}
|
|
||||||
next[i] = k;
|
|
||||||
|
|
||||||
}
|
|
||||||
return next;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
这篇文章真的写了很久很久,觉得还不错的话,就麻烦您点个赞吧,大家也可以去我的公众号看我的所有文章,每个都有动图解析,公众号:[袁厨的算法小屋](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/qrcode_for_gh_1f36d2ef6df9_258.5lojyphpkso0.jpg)
|
|
||||||
|
|
||||||
@ -1,100 +0,0 @@
|
|||||||
### **希尔排序 (Shell's Sort)**
|
|
||||||
|
|
||||||
我们在之前说过直接插入排序在记录基本有序的时候和元素较少时效率是很高的,基本有序时,只需执行少量的插入操作,就可以完成整个记录的排序工作。当元素较少时,效率也很高,就比如我们经常用的 Arrays.sort (),当元素个数少于47时,使用的排序算法就是直接插入排序。那么直接希尔排序和直接插入排序有什么关系呢?
|
|
||||||
|
|
||||||
希尔排序是**插入排序**的一种,又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序的高级变形,其思想简单点说就是有跨度的插入排序,这个跨度会逐渐变小,直到变为 1,变为 1 时记录也就基本有序,这时用到的也就是我们之前讲的直接插入排序了。
|
|
||||||
|
|
||||||
基本有序:就是小的关键字基本在前面,大的关键字基本在后面,不大不小的基本在中间。见下图。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们已经了解了希尔排序的基本思想,下面我们通过一个绘图来描述下其执行步骤。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
先逐步分组进行粗调,在进行直接插入排序的思想就是希尔排序。我们刚才的分组跨度(4,2,1)被称为希尔排序的增量,我们上面用到的是逐步折半的增量方法,这也是在发明希尔排序时提出的一种朴素方法,被称为希尔增量,
|
|
||||||
|
|
||||||
下面我们用动图模拟下使用希尔增量的希尔排序的执行过程
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
大家可能看了视频模拟,也不是特别容易写出算法代码,不过你们看到代码肯定会很熟悉滴。
|
|
||||||
|
|
||||||
**希尔排序代码**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
int increment = nums.length;
|
|
||||||
//注意看结束条件
|
|
||||||
while (increment > 1) {
|
|
||||||
//这里可以自己设置
|
|
||||||
increment = increment / 2;
|
|
||||||
//根据增量分组
|
|
||||||
for (int i = 0; i < increment; ++i) {
|
|
||||||
//这快是不是有点面熟,回去看看咱们的插入排序
|
|
||||||
for (int j = i + increment; j < nums.length; ++j) {
|
|
||||||
int temp = nums[j];
|
|
||||||
int k;
|
|
||||||
for (k = j - increment; k >= 0; k -= increment) {
|
|
||||||
if (temp < nums[k]) {
|
|
||||||
nums[k+increment] = nums[k];
|
|
||||||
continue;
|
|
||||||
}
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
nums[k+increment] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
我们刚才说,我们的增量可以自己设置的,我们上面的例子是用的希尔增量,下面我们看这个例子,看看使用希尔增量会出现什么问题。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们发现无论是以 4 为增量,还是以 2 为增量,每组内部的元素没有任何交换。直到增量为 1 时,数组才会按照直接插入排序进行调整。所以这种情况希尔排序的效率是低于直接插入排序呢?
|
|
||||||
|
|
||||||
我们的希尔增量因为每一轮之间是等比的,所以会有盲区,这里增量的选取就非常关键了。
|
|
||||||
|
|
||||||
下面给大家介绍两个比较有代表性的 Sedgewick 增量和 Hibbard 增量
|
|
||||||
|
|
||||||
Sedgewick 增量序列如下:
|
|
||||||
|
|
||||||
1,5,19,41,109.。。。
|
|
||||||
|
|
||||||
通项公式 9*4^k - 9*2^
|
|
||||||
|
|
||||||
利用此种增量方式的希尔排序,最坏时间复杂度是O(n^(4/3))
|
|
||||||
|
|
||||||
Hibbard增量序列如下:
|
|
||||||
|
|
||||||
1,3,7,15......
|
|
||||||
|
|
||||||
通项公式2 ^ k-1
|
|
||||||
|
|
||||||
利用此种增量方式的希尔排序,最坏时间复杂度为O(n^(3/2))
|
|
||||||
|
|
||||||
上面是两种比较具有代表性的增量方式,可究竟应该选取怎样的增量才是最好,目前还是一个数学难题。不过我们需要注意的一点,就是增量序列的最后一个增量值必须等于1才行。
|
|
||||||
|
|
||||||
**希尔排序时间复杂度分析**
|
|
||||||
|
|
||||||
希尔排序的时间复杂度跟增量序列的选择有关,范围为 O(n^(1.3-2)) 在此之前的排序算法时间复杂度基本都是O(n^2),希尔排序是突破这个时间复杂度的第一批算法之一。
|
|
||||||
|
|
||||||
**希尔排序空间复杂度分析**
|
|
||||||
|
|
||||||
根据我们的视频可知希尔排序的空间复杂度为 O(1),
|
|
||||||
|
|
||||||
**希尔排序的稳定性分析**
|
|
||||||
|
|
||||||
我们见下图,一起来分析下希尔排序的稳定性。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
通过上图,可知,如果我们选用 4 为跨度的话,交换后,两个相同元素 2 的相对位置会发生改变,所以希尔排序是一个不稳定的排序
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
@ -1,178 +0,0 @@
|
|||||||
### **归并排序**
|
|
||||||
|
|
||||||
归并排序是必须要掌握的排序算法,也算是面试高频考点,下面我们就一起来扒一扒归并排序吧,原理很简单,大家一下就能搞懂。
|
|
||||||
|
|
||||||
袁记菜馆内
|
|
||||||
|
|
||||||
第 23 届食神争霸赛开赛啦!
|
|
||||||
|
|
||||||
袁厨想在自己排名前4的分店中,挑选一个最优秀的厨师来参加食神争霸赛,选拔规则如下。
|
|
||||||
|
|
||||||
第一场 PK:每个分店选出两名厨师,首先进行店内 PK,选出店内里的胜者
|
|
||||||
|
|
||||||
第二场 PK: 然后店内的优胜者代表分店挑战其他某一分店的胜者(半决赛)
|
|
||||||
|
|
||||||
第三场 PK:最后剩下的两名胜者进行PK,选出最后的胜者。
|
|
||||||
|
|
||||||
示意图如下
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
上面的例子大家应该不会陌生吧,其实我们归并排序和食神选拔赛的流程是有些相似的,下面我们一起来看一下吧
|
|
||||||
|
|
||||||
归并这个词语的含义就是合并,并入的意思,而在我们的数据结构中的定义是将**两个或两个以上的有序表和成一个新的有序表**。而我们这里说的归并排序就是使用归并的思想实现的排序方法。
|
|
||||||
|
|
||||||
归并排序使用的就是分治思想。顾名思义就是分而治之,将一个大问题分解成若干个小的子问题来解决。小的子问题解决了,大问题也就解决了。分治后面会专门写一篇文章进行描述滴,这里先简单提一下。
|
|
||||||
|
|
||||||
下面我们通过一个图片来描述一下归并排序的数据变换情况,见下图。
|
|
||||||
|
|
||||||
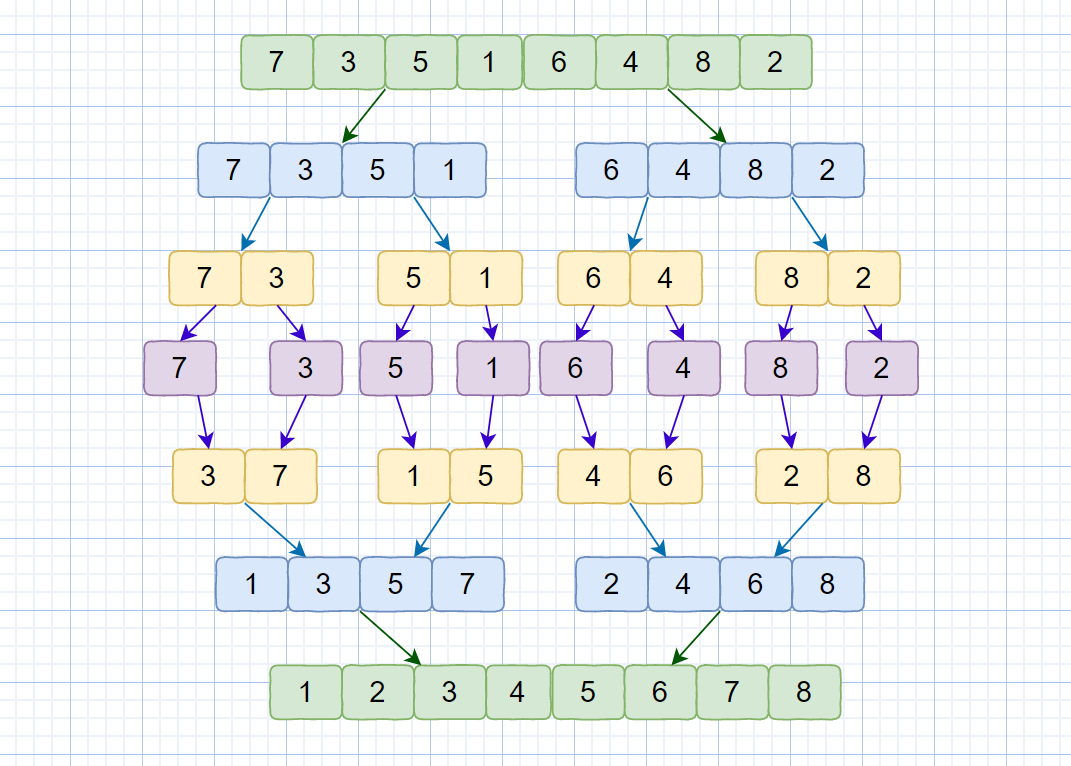
|
|
||||||
|
|
||||||
我们简单了解了归并排序的思想,从上面的描述中,我们可以知道算法的归并过程是比较难实现的,这也是这个算法的重点,看完我们这个视频就能懂个大概啦。
|
|
||||||
|
|
||||||
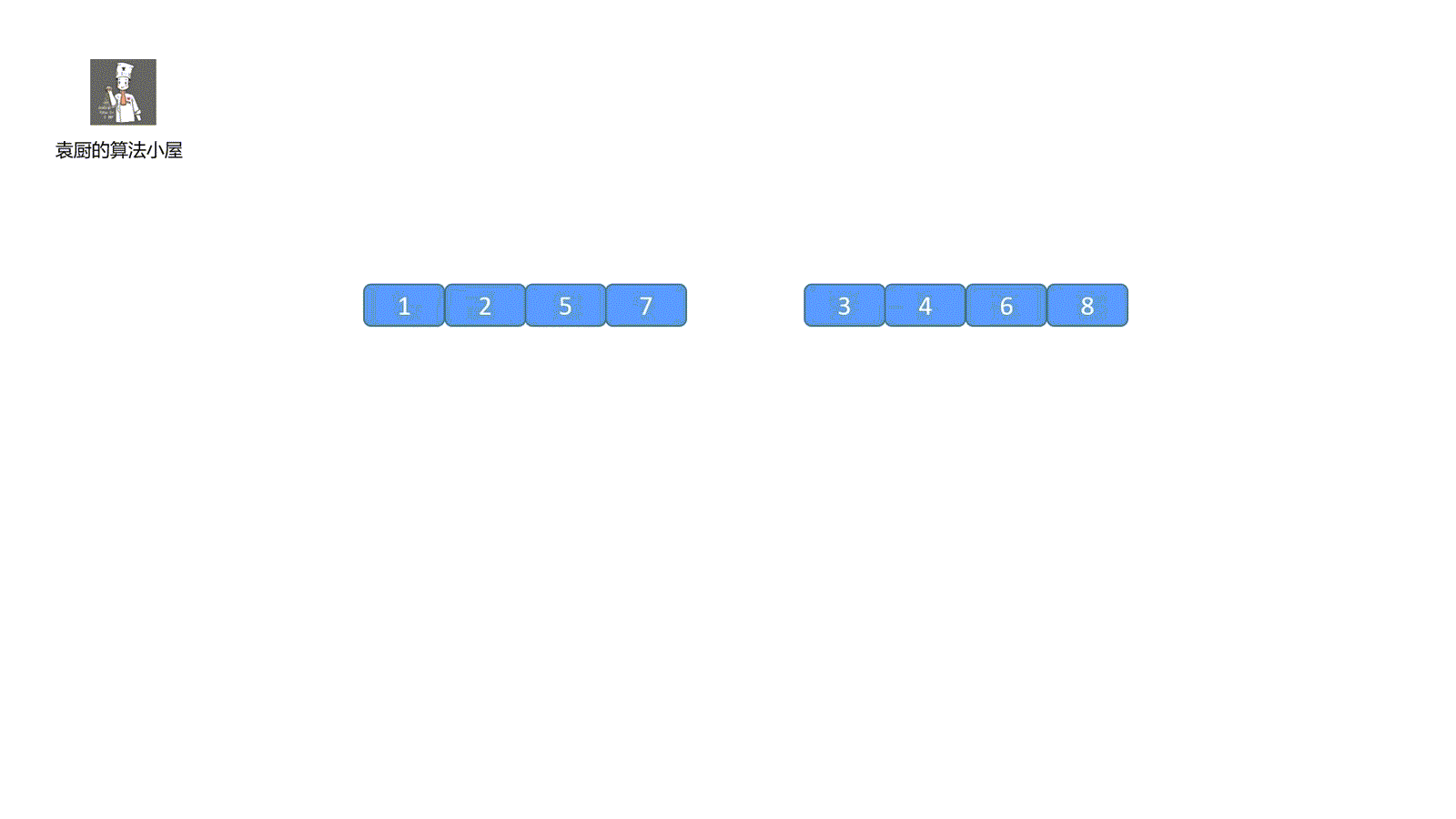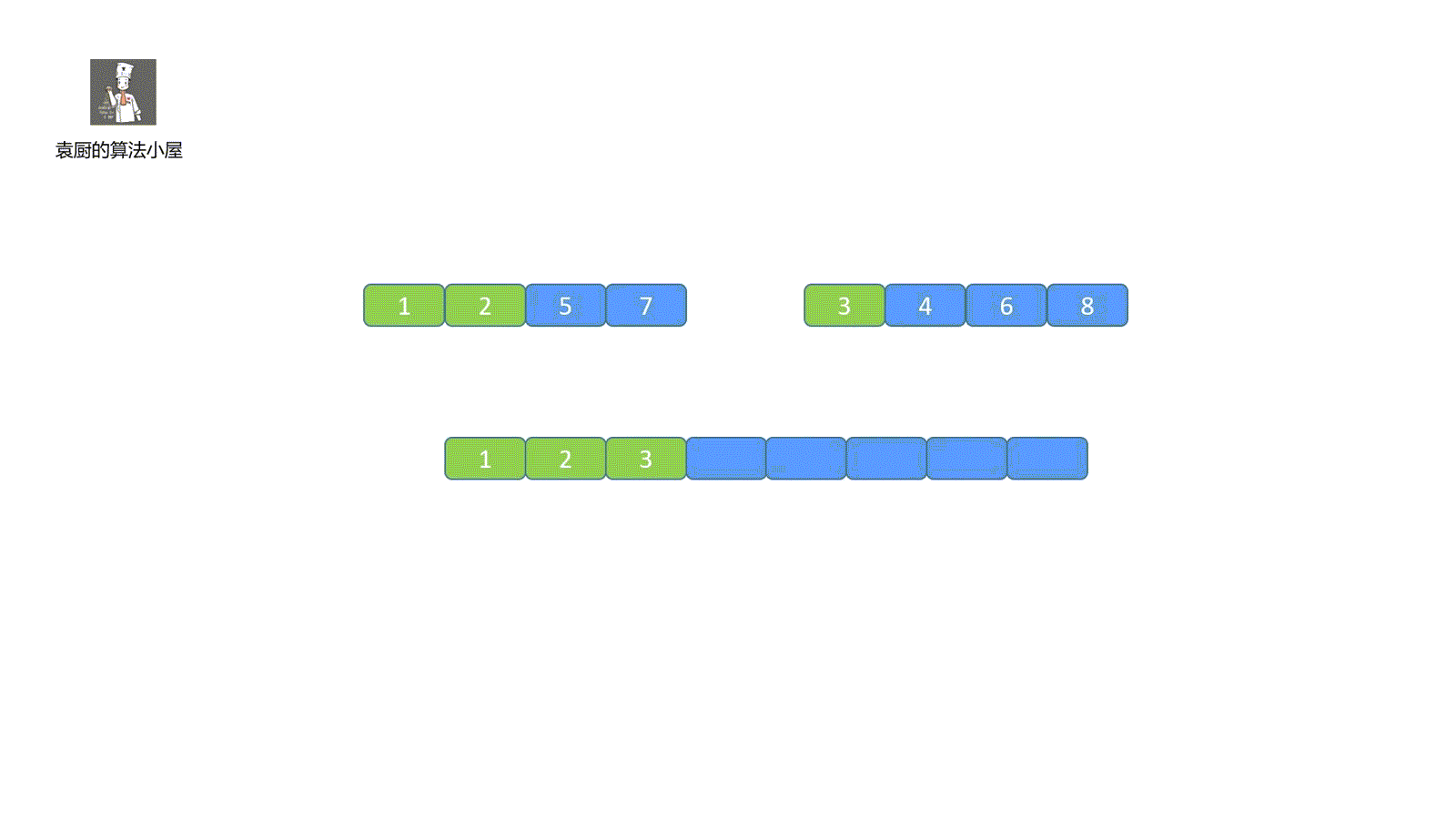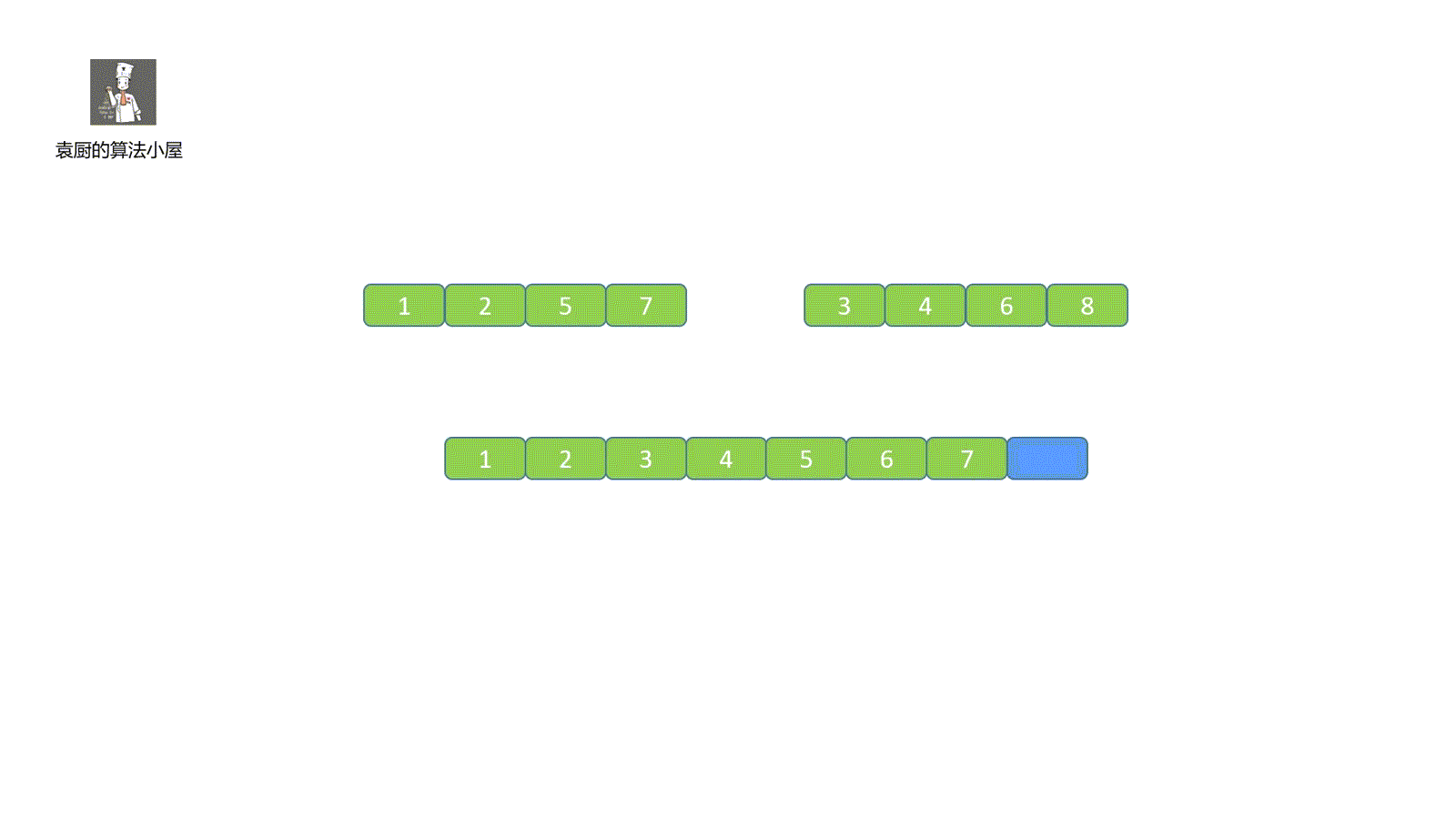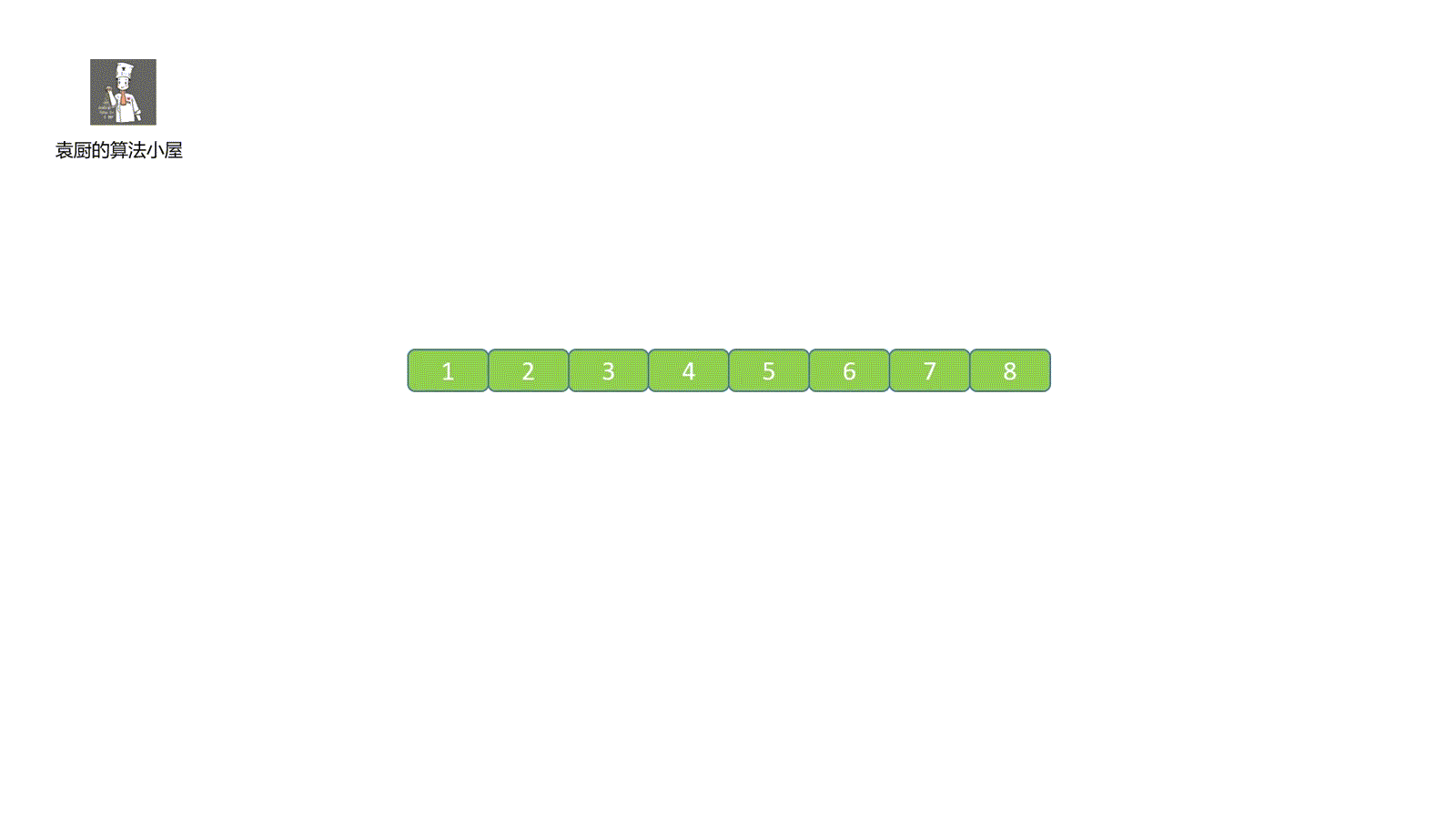
|
|
||||||
|
|
||||||
视频中归并步骤大家有没有看懂呀,没看懂也不用着急,下面我们一起来拆解一下,归并共有三步走。
|
|
||||||
|
|
||||||
第一步:创建一个额外大集合用于存储归并结果,长度则为那两个小集合的和,从视频中也可以看的出
|
|
||||||
|
|
||||||
第二步:我们从左自右比较两个指针指向的值,将较小的那个存入大集合中,存入之后指针移动,并继续比较,直到某一小集合的元素全部都存到大集合中。见下图
|
|
||||||
|
|
||||||
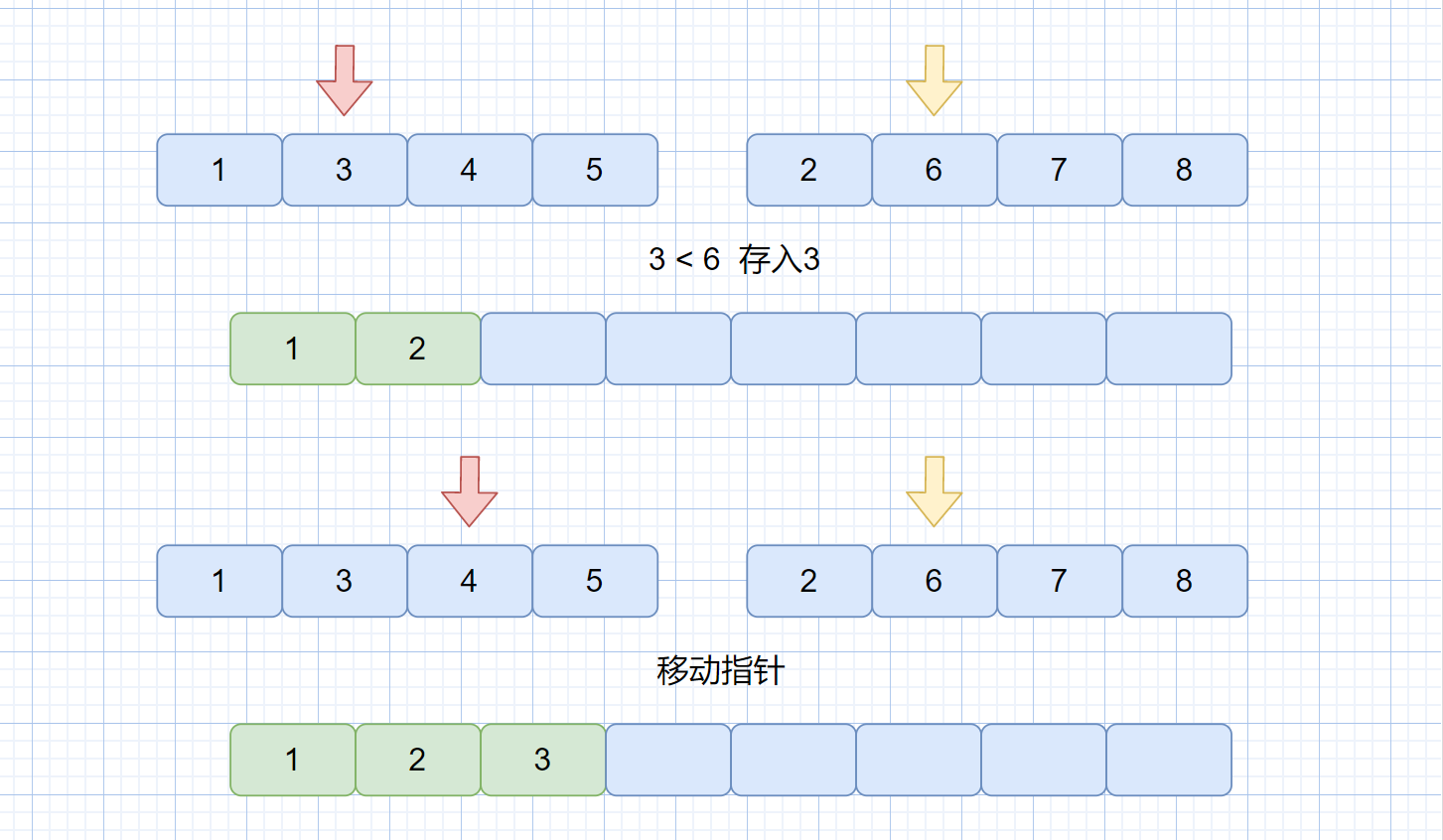
|
|
||||||
|
|
||||||
第三步:当某一小集合元素全部放入大集合中,则需将另一小集合中剩余的所有元素存到大集合中,见下图
|
|
||||||
|
|
||||||
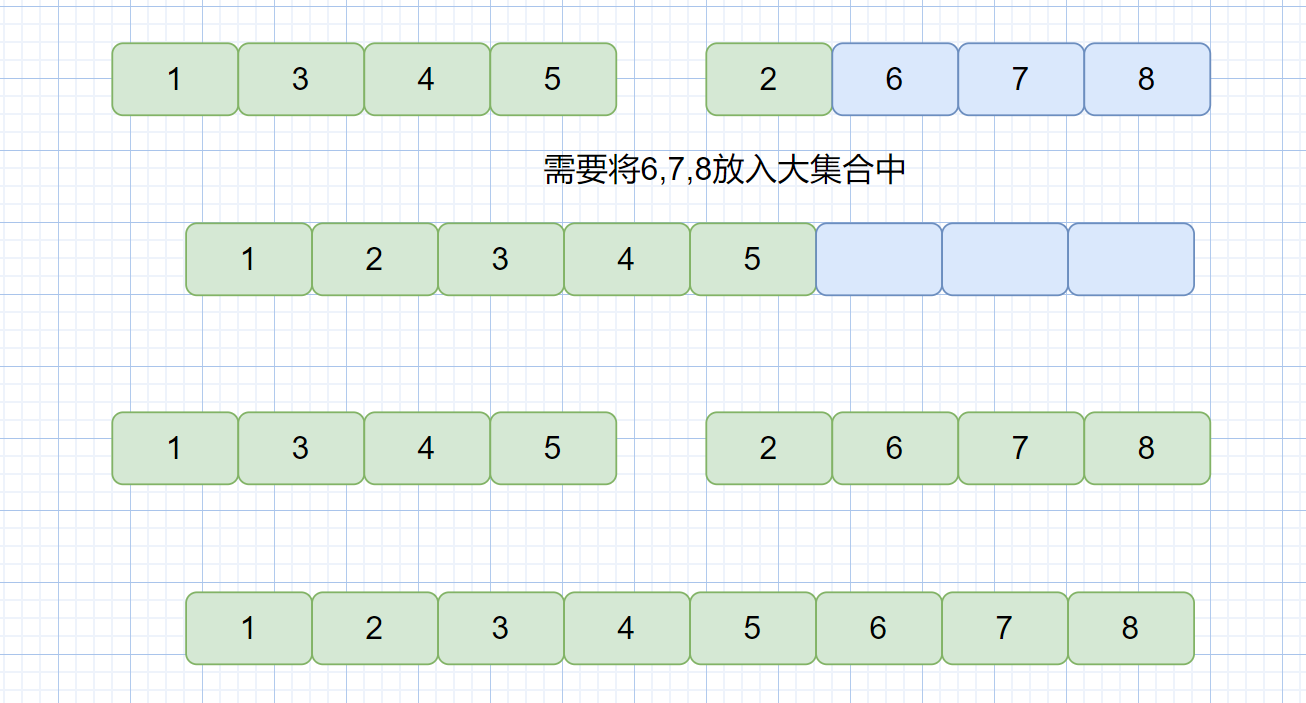
|
|
||||||
|
|
||||||
好啦,看完视频和图解是不是能够写出个大概啦,了解了算法原理之后代码写起来就很简单啦,
|
|
||||||
|
|
||||||
下面我们看代码吧。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
mergeSort(nums,0,nums.length-1);
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
public void mergeSort(int[] arr, int left, int right) {
|
|
||||||
if (left < right) {
|
|
||||||
int mid = left + ((right - left) >> 1);
|
|
||||||
mergeSort(arr,left,mid);
|
|
||||||
mergeSort(arr,mid+1,right);
|
|
||||||
merge(arr,left,mid,right);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//归并
|
|
||||||
public void merge(int[] arr,int left, int mid, int right) {
|
|
||||||
//第一步,定义一个新的临时数组
|
|
||||||
int[] temparr = new int[right -left + 1];
|
|
||||||
int temp1 = left, temp2 = mid + 1;
|
|
||||||
int index = 0;
|
|
||||||
//对应第二步,比较每个指针指向的值,小的存入大集合
|
|
||||||
while (temp1 <= mid && temp2 <= right) {
|
|
||||||
if (arr[temp1] <= arr[temp2]) {
|
|
||||||
temparr[index++] = arr[temp1++];
|
|
||||||
} else {
|
|
||||||
temparr[index++] = arr[temp2++];
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//对应第三步,将某一小集合的剩余元素存到大集合中
|
|
||||||
if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
|
|
||||||
if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1); //将大集合的元素复制回原数组
|
|
||||||
System.arraycopy(temparr,0,arr,0+left,right-left+1);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**归并排序时间复杂度分析**
|
|
||||||
|
|
||||||
我们一趟归并,需要将两个小集合的长度放到大集合中,则需要将待排序序列中的所有记录扫描一遍所以时间复杂度为O(n)。归并排序把集合一层一层的折半分组,则由完全二叉树的深度可知,整个排序过程需要进行 logn(向上取整)次,则总的时间复杂度为 O(nlogn)。另外归并排序的执行效率与要排序的原始数组的有序程度无关,所以在最好,最坏,平均情况下时间复杂度均为 O(nlogn) 。虽然归并排序时间复杂度很稳定,但是他的应用范围却不如快速排序广泛,这是因为归并排序不是原地排序算法,空间复杂度不为 O(1),那么他的空间复杂度为多少呢?
|
|
||||||
|
|
||||||
**归并排序的空间复杂度分析**
|
|
||||||
|
|
||||||
归并排序所创建的临时结合都会在方法结束时释放,单次归并排序的最大空间是 n ,所以归并排序的空间复杂度为 O(n).
|
|
||||||
|
|
||||||
**归并排序的稳定性分析**
|
|
||||||
|
|
||||||
归并排序的稳定性,要看我们的 merge 函数,我们代码中设置了 arr[temp1] <= arr[temp2] ,当两个元素相同时,先放入arr[temp1] 的值到大集合中,所以两个相同元素的相对位置没有发生改变,所以归并排序是稳定的排序算法。
|
|
||||||
|
|
||||||
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|
|
||||||
| -------- | -------------- | -------------- | -------------- | ---------- | -------- |
|
|
||||||
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
|
|
||||||
|
|
||||||
等等还没完嘞,不要走。
|
|
||||||
|
|
||||||
归并排序的递归实现是比较常见的,也是比较容易理解的,下面我们一起来扒一下归并排序的迭代写法。看看他是怎么实现的。
|
|
||||||
|
|
||||||
我们通过一个视频来了解下迭代方法的思想,
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
是不是通过视频了解个大概啦,下面我们来对视频进行解析。
|
|
||||||
|
|
||||||
迭代实现的归并排序是将小集合合成大集合,小集合大小为 1,2,4,8,.....。依次迭代,见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
比如此时小集合大小为 1 。两个小集合分别为 [3],[1]。然后我们根据合并规则,见第一个视频,将[3],[1]合并到临时数组中,则小的先进,则实现了排序,然后再将临时数组的元素复制到原来数组中。则实现了一次合并。
|
|
||||||
|
|
||||||
下面则继续合并[4],[6]。具体步骤一致。所有的小集合合并完成后,则小集合的大小变为 2,继续执行刚才步骤,见下图。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时子集合的大小为 2 ,则为 [2,5],[1,3] 继续按照上面的规则合并到临时数组中完成排序。 这就是迭代法的具体执行过程,
|
|
||||||
|
|
||||||
下面我们直接看代码吧。
|
|
||||||
|
|
||||||
注:递归法和迭代法的 merge函数代码一样。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray (int[] nums) {
|
|
||||||
//代表子集合大小,1,2,4,8,16.....
|
|
||||||
int k = 1;
|
|
||||||
int len = nums.length;
|
|
||||||
while (k < len) {
|
|
||||||
mergePass(nums,k,len);
|
|
||||||
k *= 2;
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
|
|
||||||
}
|
|
||||||
public void mergePass (int[] array, int k, int len) {
|
|
||||||
|
|
||||||
int i;
|
|
||||||
for (i = 0; i < len-2*k; i += 2*k) {
|
|
||||||
//归并
|
|
||||||
merge(array,i,i+k-1,i+2*k-1);
|
|
||||||
}
|
|
||||||
//归并最后两个序列
|
|
||||||
if (i + k < len) {
|
|
||||||
merge(array,i,i+k-1,len-1);
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
public void merge (int[] arr,int left, int mid, int right) {
|
|
||||||
//第一步,定义一个新的临时数组
|
|
||||||
int[] temparr = new int[right -left + 1];
|
|
||||||
int temp1 = left, temp2 = mid + 1;
|
|
||||||
int index = 0;
|
|
||||||
//对应第二步,比较每个指针指向的值,小的存入大集合
|
|
||||||
while (temp1 <= mid && temp2 <= right) {
|
|
||||||
if (arr[temp1] <= arr[temp2]) {
|
|
||||||
temparr[index++] = arr[temp1++];
|
|
||||||
} else {
|
|
||||||
temparr[index++] = arr[temp2++];
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//对应第三步,将某一小集合的剩余元素存到大集合中
|
|
||||||
if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
|
|
||||||
if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);
|
|
||||||
//将大集合的元素复制回原数组
|
|
||||||
System.arraycopy(temparr,0,arr,0+left,right-left+1);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
@ -1,424 +0,0 @@
|
|||||||
### 快速排序
|
|
||||||
|
|
||||||
今天我们来说一下快速排序,这个排序算法也是面试的高频考点,原理很简单,我们一起来扒一下他吧。
|
|
||||||
|
|
||||||
我们先来说一下快速排序的基本思想。
|
|
||||||
|
|
||||||
1.先从数组中找一个基准数
|
|
||||||
|
|
||||||
2.让其他比它大的元素移动到数列一边,比他小的元素移动到数列另一边,从而把数组拆解成两个部分。
|
|
||||||
|
|
||||||
3.再对左右区间重复第二步,直到各区间只有一个数。
|
|
||||||
|
|
||||||
见下图
|
|
||||||
|
|
||||||
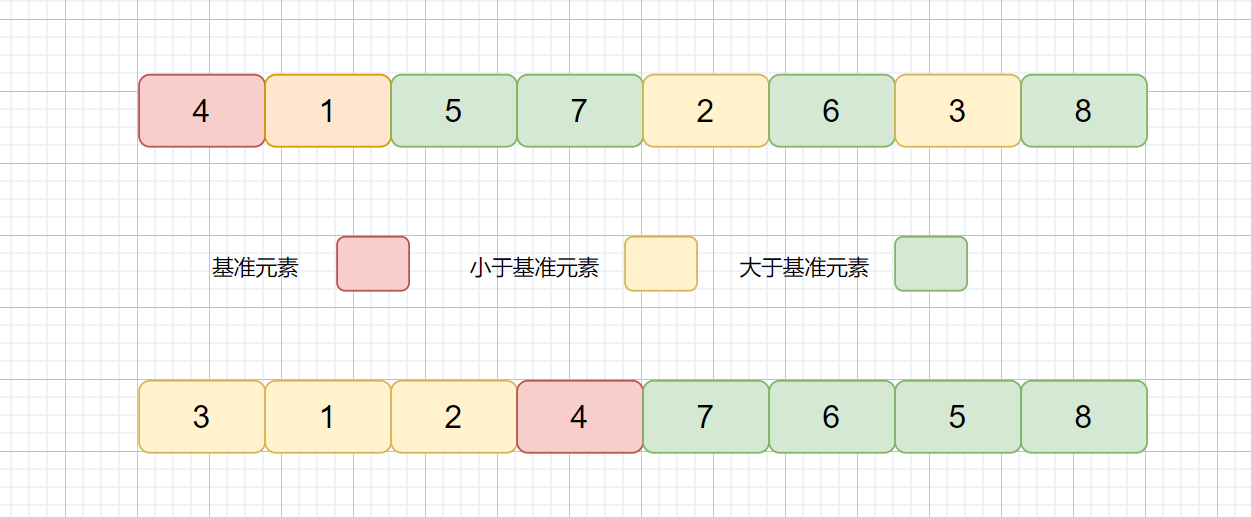
|
|
||||||
|
|
||||||
上图则为一次快排示意图,下面我们再利用递归,分别对左半边区间也就是 [3,1,2] 和右半区间 [7,6,5,8] 执行上诉过程,直至区间缩小为 1 也就是第三条,则此时所有的数据都有序。
|
|
||||||
|
|
||||||
简单来说就是我们利用基准数通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比基准数小,另一部分记录的关键字均比基准数大,然后分别对这两部分记录继续进行排序,进而达到有序。
|
|
||||||
|
|
||||||
我们现在应该了解了快速排序的思想,那么大家还记不记得我们之前说过的归并排序,他们两个用到的都是分治思想,那他们两个有什么不同呢?见下图
|
|
||||||
|
|
||||||
注:快速排序我们以序列的第一个元素作为基准数
|
|
||||||
|
|
||||||
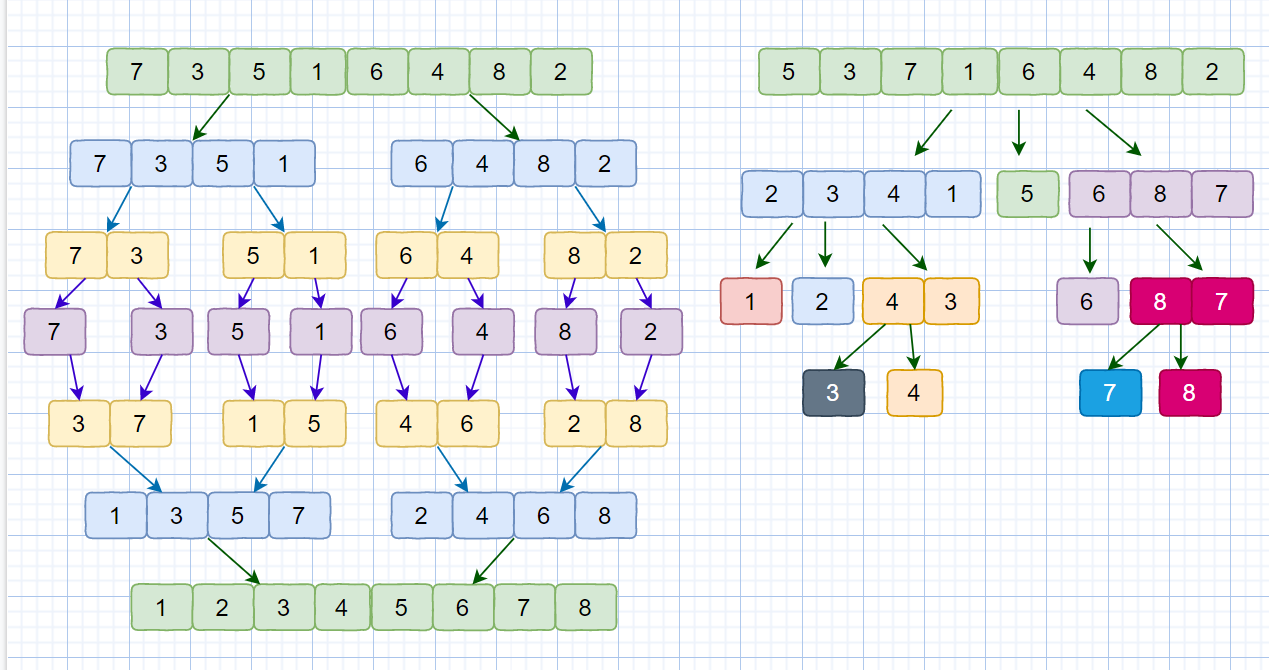
|
|
||||||
|
|
||||||
虽然归并排序和快速排序都用到了分治思想,但是归并排序是自下而上的,先处理子问题,然后再合并,将小集合合成大集合,最后实现排序。而快速排序是由上到下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。我们前面讲过,归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题
|
|
||||||
|
|
||||||
我们根据思想可知,排序算法的核心就是如何利用基准数将记录分区,这里我们主要介绍两种容易理解的方法,一种是挖坑填数,另一种是利用双指针思想进行元素交换。
|
|
||||||
|
|
||||||
下面我们先来介绍下挖坑填数的分区方法
|
|
||||||
|
|
||||||
基本思想是我们首先以序列的第一个元素为基准数,然后将该位置挖坑,下面判断 nums[hight] 是否大于基准数,如果大于则左移 hight 指针,直至找到一个小于基准数的元素,将其填入之前的坑中,则 hight 位置会出现一个新的坑,此时移动 low 指针,找到大于基准数的元素,填入新的坑中。不断迭代直至完成分区。
|
|
||||||
|
|
||||||
大家直接看我们的视频模拟吧,一目了然。
|
|
||||||
|
|
||||||
注:为了便于理解所以采取了挖坑的形式展示
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
是不是很容易就理解啦,下面我们直接看代码吧。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
|
|
||||||
quickSort(nums,0,nums.length-1);
|
|
||||||
return nums;
|
|
||||||
|
|
||||||
}
|
|
||||||
public void quickSort (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
if (low < hight) {
|
|
||||||
int index = partition(nums,low,hight);
|
|
||||||
quickSort(nums,low,index-1);
|
|
||||||
quickSort(nums,index+1,hight);
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
public int partition (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
int pivot = nums[low];
|
|
||||||
while (low < hight) {
|
|
||||||
//移动hight指针
|
|
||||||
while (low < hight && nums[hight] >= pivot) {
|
|
||||||
hight--;
|
|
||||||
}
|
|
||||||
//填坑
|
|
||||||
if (low < hight) nums[low] = nums[hight];
|
|
||||||
while (low < hight && nums[low] <= pivot) {
|
|
||||||
low++;
|
|
||||||
}
|
|
||||||
//填坑
|
|
||||||
if (low < hight) nums[hight] = nums[low];
|
|
||||||
}
|
|
||||||
//基准数放到合适的位置
|
|
||||||
nums[low] = pivot;
|
|
||||||
return low;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
下面我们来看一下交换思路,原理一致,实现也比较简单。
|
|
||||||
|
|
||||||
见下图。
|
|
||||||
|
|
||||||
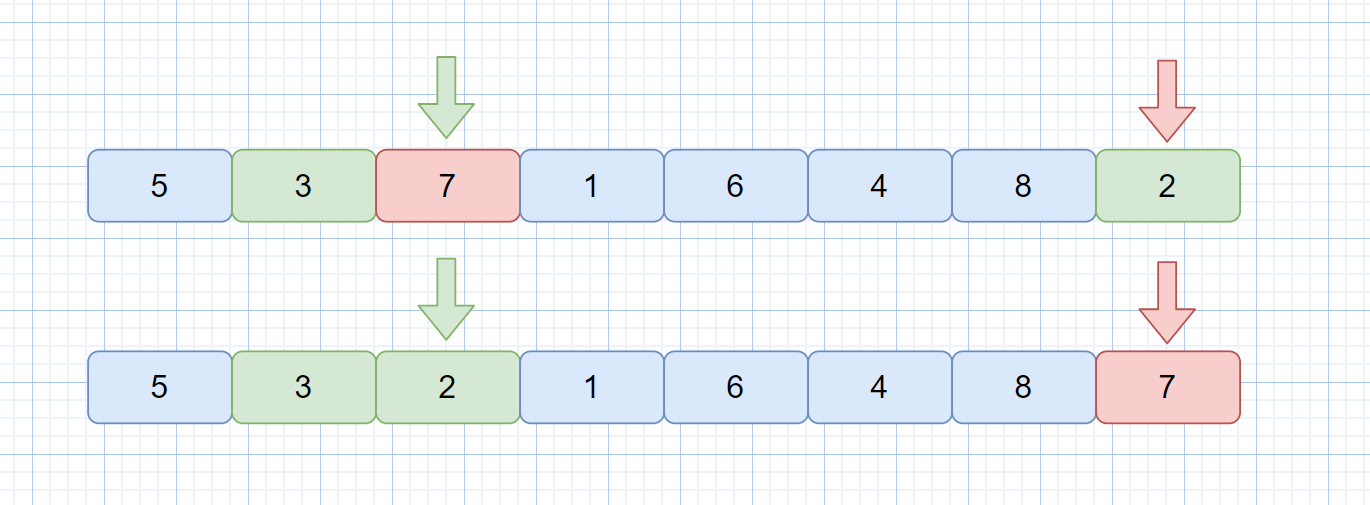
|
|
||||||
|
|
||||||
其实这种方法,算是对上面方法的挖坑填坑步骤进行合并,low 指针找到大于 pivot 的元素,hight 指针找到小于 pivot 的元素,然后两个元素交换位置,最后再将基准数归位。两种方法都很容易理解和实现,即使是完全没有学习过快速排序的同学,理解了思想之后也能自己动手实现,下面我们继续用视频模拟下这种方法的执行过程吧。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
两种方法都很容易实现,对新手非常友好,大家可以自己去 AC 一下啊。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray (int[] nums) {
|
|
||||||
|
|
||||||
quickSort(nums,0,nums.length-1);
|
|
||||||
return nums;
|
|
||||||
|
|
||||||
}
|
|
||||||
|
|
||||||
public void quickSort (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
if (low < hight) {
|
|
||||||
int index = partition(nums,low,hight);
|
|
||||||
quickSort(nums,low,index-1);
|
|
||||||
quickSort(nums,index+1,hight);
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
|
|
||||||
public int partition (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
int pivot = nums[low];
|
|
||||||
int start = low;
|
|
||||||
|
|
||||||
while (low < hight) {
|
|
||||||
while (low < hight && nums[hight] >= pivot) hight--;
|
|
||||||
while (low < hight && nums[low] <= pivot) low++;
|
|
||||||
if (low >= hight) break;
|
|
||||||
swap(nums, low, hight);
|
|
||||||
}
|
|
||||||
//基准值归位
|
|
||||||
swap(nums,start,low);
|
|
||||||
return low;
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**快速排序的时间复杂度分析**
|
|
||||||
|
|
||||||
快排也是用递归来实现的。所以快速排序的时间性能取决于快速排序的递归树的深度。如果每次分区操作,都能正好把数组分成大小接近相等的两个小区间,那么此时的递归树是平衡的,性能也较好,递归树的深度也就和之前归并排序求解方法一致,然后我们每一次分区需要对数组扫描一遍,做 n 次比较,所以最优情况下,快排的时间复杂度是 O(nlogn)。
|
|
||||||
|
|
||||||
但是大多数情况下我们不能划分的很均匀,比如数组为正序或者逆序时,即 [1,2,3,4] 或 [4,3,2,1] 时,此时为最坏情况,那么此时我们则需要递归调用 n-1 次,此时的时间复杂度则退化到了 O(n^2)。
|
|
||||||
|
|
||||||
**快速排序的空间复杂度分析**
|
|
||||||
|
|
||||||
快速排序主要时递归造成的栈空间的使用,最好情况时其空间复杂度为O (logn),对应递归树的深度。最坏情况时则需要 n-1 次递归调用,此时空间复杂度为O(n).
|
|
||||||
|
|
||||||
**快速排序的稳定性分析**
|
|
||||||
|
|
||||||
快速排序是一种不稳定的排序算法,因为其关键字的比较和交换是跳跃进行的,见下图。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时无论使用哪一种方法,第一次排序后,黄色的 1 都会跑到红色 1 的前面,所以快速排序是不稳定的排序算法。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
好啦,快速排序我们掌握的差不多了,下面我们一起来看看如何对其优化吧。
|
|
||||||
|
|
||||||
**快速排序的迭代写法**
|
|
||||||
|
|
||||||
该方法实现也是比较简单的,借助了栈来实现,很容易实现。主要利用了先进后出的特性,这里需要注意的就是入栈的顺序,这里算是一个小细节,需要注意一下。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
Stack<Integer> stack = new Stack<>();
|
|
||||||
stack.push(nums.length - 1);
|
|
||||||
stack.push(0);
|
|
||||||
while (!stack.isEmpty()) {
|
|
||||||
int low = stack.pop();
|
|
||||||
int hight = stack.pop();
|
|
||||||
|
|
||||||
if (low < hight) {
|
|
||||||
int index = partition(nums, low, hight);
|
|
||||||
stack.push(index - 1);
|
|
||||||
stack.push(low);
|
|
||||||
stack.push(hight);
|
|
||||||
stack.push(index + 1);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
|
|
||||||
public int partition (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
int pivot = nums[low];
|
|
||||||
int start = low;
|
|
||||||
while (low < hight) {
|
|
||||||
|
|
||||||
while (low < hight && nums[hight] >= pivot) hight--;
|
|
||||||
while (low < hight && nums[low] <= pivot) low++;
|
|
||||||
if (low >= hight) break;
|
|
||||||
swap(nums, low, hight);
|
|
||||||
}
|
|
||||||
swap(nums,start,low);
|
|
||||||
return low;
|
|
||||||
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**快速排序优化**
|
|
||||||
|
|
||||||
**三数取中法**
|
|
||||||
|
|
||||||
我们在上面的例子中选取的都是 nums[low] 做为我们的基准值,那么当我们遇到特殊情况时呢?见下图
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们按上面的方法,选取第一个元素做为基准元素,那么我们执行一轮排序后,发现仅仅是交换了 2 和 7 的位置,这是因为 7 为序列的最大值。所以我们的 pivot 的选取尤为重要,选取时应尽量避免选取序列的最大或最小值做为基准值。则我们可以利用三数取中法来选取基准值。
|
|
||||||
|
|
||||||
也就是选取三个元素中的中间值放到 nums[low] 的位置,做为基准值。这样就避免了使用最大值或最小值做为基准值。
|
|
||||||
|
|
||||||
所以我们可以加上这几行代码实现三数取中法。
|
|
||||||
|
|
||||||
```java
|
|
||||||
int mid = low + ((hight-low) >> 1);
|
|
||||||
if (nums[low] > nums[hight]) swap(nums,low,hight);
|
|
||||||
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
|
|
||||||
if (nums[mid] > nums[low]) swap(nums,mid,low);
|
|
||||||
```
|
|
||||||
|
|
||||||
其含义就是让我们将中间元素放到 nums[low] 位置做为基准值,最大值放到 nums[hight],最小值放到 nums[mid],即 [4,2,3] 经过上面代码处理后,则变成了 [3,2,4].此时我们选取 3 做为基准值,这样也就避免掉了选取最大或最小值做为基准值的情况。
|
|
||||||
|
|
||||||
**三数取中法**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
quickSort(nums,0,nums.length-1);
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
public void quickSort (int[] nums, int low, int hight) {
|
|
||||||
if (low < hight) {
|
|
||||||
int index = partition(nums,low,hight);
|
|
||||||
quickSort(nums,low,index-1);
|
|
||||||
quickSort(nums,index+1,hight);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
public int partition (int[] nums, int low, int hight) {
|
|
||||||
//三数取中,大家也可以使用其他方法
|
|
||||||
int mid = low + ((hight-low) >> 1);
|
|
||||||
if (nums[low] > nums[hight]) swap(nums,low,hight);
|
|
||||||
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
|
|
||||||
if (nums[mid] > nums[low]) swap(nums,mid,low);
|
|
||||||
//下面和之前一样,仅仅是多了上面几行代码
|
|
||||||
int pivot = nums[low];
|
|
||||||
int start = low;
|
|
||||||
while (low < hight) {
|
|
||||||
while (low < hight && nums[hight] >= pivot) hight--;
|
|
||||||
while (low < hight && nums[low] <= pivot) low++;
|
|
||||||
if (low >= hight) break;
|
|
||||||
swap(nums, low, hight);
|
|
||||||
}
|
|
||||||
swap(nums,start,low);
|
|
||||||
return low;
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**和插入排序搭配使用**
|
|
||||||
|
|
||||||
我们之前说过,插入排序在元素个数较少时效率是最高的,所以当元素数量较少时,快速排序反而不如插入排序好用,所以我们可以设定一个阈值,当元素个数大于阈值时使用快速排序,小于等于该阈值时则使用插入排序。我们设定阈值为 7 。
|
|
||||||
|
|
||||||
**三数取中+插入排序**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
private static final int INSERTION_SORT_MAX_LENGTH = 7;
|
|
||||||
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
quickSort(nums,0,nums.length-1);
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
|
|
||||||
public void quickSort (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
if (hight - low <= INSERTION_SORT_MAX_LENGTH) {
|
|
||||||
insertSort(nums,low,hight);
|
|
||||||
return;
|
|
||||||
}
|
|
||||||
int index = partition(nums,low,hight);
|
|
||||||
quickSort(nums,low,index-1);
|
|
||||||
quickSort(nums,index+1,hight);
|
|
||||||
}
|
|
||||||
|
|
||||||
public int partition (int[] nums, int low, int hight) {
|
|
||||||
//三数取中,大家也可以使用其他方法
|
|
||||||
int mid = low + ((hight-low) >> 1);
|
|
||||||
if (nums[low] > nums[hight]) swap(nums,low,hight);
|
|
||||||
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
|
|
||||||
if (nums[mid] > nums[low]) swap(nums,mid,low);
|
|
||||||
int pivot = nums[low];
|
|
||||||
int start = low;
|
|
||||||
while (low < hight) {
|
|
||||||
while (low < hight && nums[hight] >= pivot) hight--;
|
|
||||||
while (low < hight && nums[low] <= pivot) low++;
|
|
||||||
if (low >= hight) break;
|
|
||||||
swap(nums, low, hight);
|
|
||||||
}
|
|
||||||
swap(nums,start,low);
|
|
||||||
return low;
|
|
||||||
}
|
|
||||||
|
|
||||||
public void insertSort (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
for (int i = low+1; i <= hight; ++i) {
|
|
||||||
int temp = nums[i];
|
|
||||||
int j;
|
|
||||||
for (j = i-1; j >= 0; --j) {
|
|
||||||
if (temp < nums[j]) {
|
|
||||||
nums[j+1] = nums[j];
|
|
||||||
continue;
|
|
||||||
}
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
nums[j+1] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
我们继续看下面这种情况
|
|
||||||
|
|
||||||
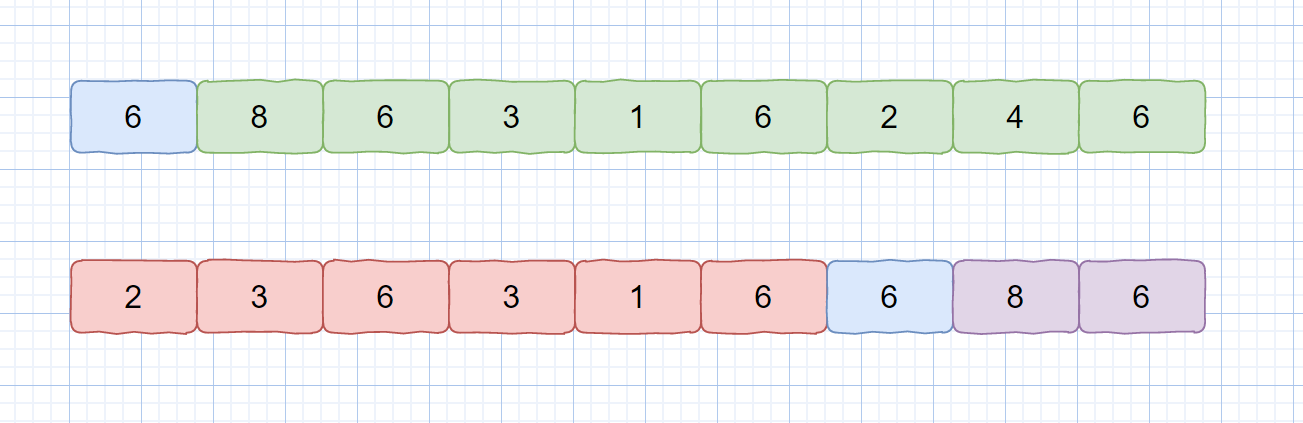
|
|
||||||
|
|
||||||
我们对其执行一次排序后,则会变成上面这种情况,然后我们继续对蓝色基准值的左区间和右区间执行相同操作。也就是 [2,3,6,3,1,6] 和 [8,6] 。我们注意观察一次排序的结果数组中是含有很多重复元素的。
|
|
||||||
|
|
||||||
那么我们为什么不能将相同元素放到一起呢?这样就能大大减小递归调用时的区间大小,见下图。
|
|
||||||
|
|
||||||
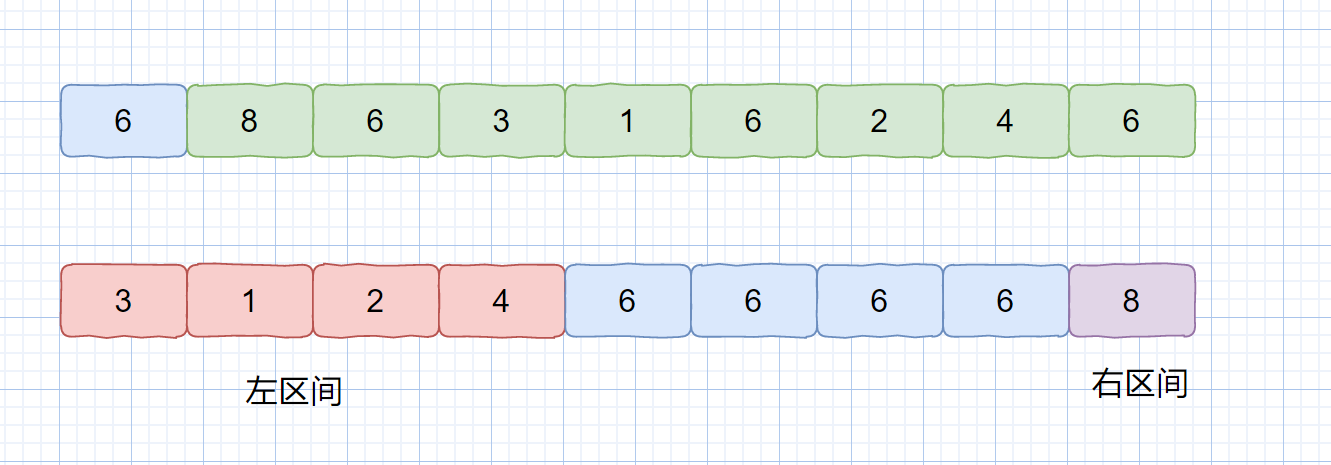
|
|
||||||
|
|
||||||
这样就减小了我们的区间大小,将数组切分成了三部分,小于基准数的左区间,大于基准数的右区间,等于基准数的中间区间。
|
|
||||||
|
|
||||||
下面我们来看一下如何达到上面的情况,我们先来进行视频模拟,模拟之后应该就能明白啦。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们来剖析一下视频,其实原理很简单,我们利用探路指针也就是 i,遇到比 pivot 大的元素,则和 right 指针进行交换,此时 right 指向的元素肯定比 pivot 大,则 right--,但是,此时我们的 nums[i] 指向的元素并不知道情况,所以我们的 i 指针不动,如果此时 nums[i] < pivot 则与 left 指针交换,注意此时我们的 left 指向的值肯定是 等于 povit的,所以交换后我们要 left++,i++, nums[i] == pivot 时,仅需要 i++ 即可,继续判断下一个元素。 我们也可以借助这个思想来解决经典的荷兰国旗问题。
|
|
||||||
|
|
||||||
好啦,我们下面直接看代码吧。
|
|
||||||
|
|
||||||
**三数取中+三向切分+插入排序**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
private static final int INSERTION_SORT_MAX_LENGTH = 7;
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
quickSort(nums,0,nums.length-1);
|
|
||||||
return nums;
|
|
||||||
|
|
||||||
}
|
|
||||||
public void quickSort(int nums[], int low, int hight) {
|
|
||||||
//插入排序
|
|
||||||
if (hight - low <= INSERTION_SORT_MAX_LENGTH) {
|
|
||||||
insertSort(nums,low,hight);
|
|
||||||
return;
|
|
||||||
}
|
|
||||||
//三数取中
|
|
||||||
int mid = low + ((hight-low) >> 1);
|
|
||||||
if (nums[low] > nums[hight]) swap(nums,low,hight);
|
|
||||||
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
|
|
||||||
if (nums[mid] > nums[low]) swap(nums,mid,low);
|
|
||||||
//三向切分
|
|
||||||
int left = low, i = low + 1, right = hight;
|
|
||||||
int pvoit = nums[low];
|
|
||||||
while (i <= right) {
|
|
||||||
if (pvoit < nums[i]) {
|
|
||||||
swap(nums,i,right);
|
|
||||||
right--;
|
|
||||||
} else if (pvoit == nums[i]) {
|
|
||||||
i++;
|
|
||||||
} else {
|
|
||||||
swap(nums,left,i);
|
|
||||||
left++;
|
|
||||||
i++;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
quickSort(nums,low,left-1);
|
|
||||||
quickSort(nums,right+1,hight);
|
|
||||||
}
|
|
||||||
public void insertSort (int[] nums, int low, int hight) {
|
|
||||||
|
|
||||||
for (int i = low+1; i <= hight; ++i) {
|
|
||||||
int temp = nums[i];
|
|
||||||
int j;
|
|
||||||
for (j = i-1; j >= 0; --j) {
|
|
||||||
if (temp < nums[j]) {
|
|
||||||
nums[j+1] = nums[j];
|
|
||||||
continue;
|
|
||||||
}
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
nums[j+1] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
好啦,一些常用的优化方法都整理出来啦,还有一些其他的优化算法九数取中,优化递归操作等就不在这里进行描述啦,感兴趣的可以自己看一下。好啦,这期的文章就到这里啦,我们下期见,拜了个拜。
|
|
||||||
|
|
||||||
@ -1,61 +0,0 @@
|
|||||||
### **直接插入排序(Straight Insertion Sort)**
|
|
||||||
|
|
||||||
袁记菜馆内
|
|
||||||
|
|
||||||
袁厨:好嘞,我们打烊啦,一起来玩会扑克牌吧。
|
|
||||||
|
|
||||||
小二:好啊,掌柜的,咱们玩会斗地主吧。
|
|
||||||
|
|
||||||
相信大家应该都玩过扑克牌吧,我们平常摸牌时,是不是一边摸牌,一边理牌,摸到新牌时,会将其插到合适的位置。这其实就是我们的插入排序思想。
|
|
||||||
|
|
||||||
直接插入排序:将一个记录插入到已经排好序的有序表中,从而得到一个新的有序表。通俗理解,我们首先将序列分成两个区间,有序区间和无序区间,我们每次在无序区间内取一个值,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间一直有序。下面我们看一下动图吧。
|
|
||||||
|
|
||||||
注:为了更清晰表达算法思想,则采用了挖掉待排序元素的形式展示,后面也会采取此形式表达。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
**直接插入排序代码**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
//注意 i 的初始值为 1,也就是第二个元素开始
|
|
||||||
for (int i = 1; i < nums.length; ++i) {
|
|
||||||
//待排序的值
|
|
||||||
int temp = nums[i];
|
|
||||||
//需要注意
|
|
||||||
int j;
|
|
||||||
for (j = i-1; j >= 0; --j) {
|
|
||||||
//找到合适位置
|
|
||||||
if (temp < nums[j]) {
|
|
||||||
nums[j+1] = nums[j];
|
|
||||||
continue;
|
|
||||||
}
|
|
||||||
//跳出循环
|
|
||||||
break;
|
|
||||||
}
|
|
||||||
//插入到合适位置,这也就是我们没有在 for 循环内定义变量的原因
|
|
||||||
nums[j+1] = temp;
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
**直接插入排序时间复杂度分析**
|
|
||||||
|
|
||||||
最好情况时,也就是有序的时候,我们不需要移动元素,每次只需要比较一次即可找到插入位置,那么最好情况时的时间复杂度为O(n)。
|
|
||||||
|
|
||||||
最坏情况时,即待排序表是逆序的情况,则此时需要比较2+3+....+n = (n+2)*(n-1)/2,移动次数也达到了最大值,3 +4+5+....n+1 = (n+4)*(n-1)/2,时间复杂度为O(n^2).
|
|
||||||
|
|
||||||
我们每次插入一个数据的时间复杂度为O(n),那么循环执行 n 次插入操作,平均时间复杂度为O(n^2)。
|
|
||||||
|
|
||||||
**直接插入排序空间复杂度分析**
|
|
||||||
|
|
||||||
根据动画可知,插入排序不需要额外的存储空间,所以其空间复杂度为O(1)
|
|
||||||
|
|
||||||
**直接插入排序稳定性分析**
|
|
||||||
|
|
||||||
我们根据代码可知,我们只会移动比 temp 值大的元素,所以我们排序后可以保证相同元素的相对位置不变。所以直接插入排序为稳定性排序算法。
|
|
||||||
|
|
||||||

|
|
||||||
@ -1,66 +0,0 @@
|
|||||||
### **简单选择排序**
|
|
||||||
|
|
||||||
我们的冒泡排序不断进行交换,通过交换完成最终的排序,我们的简单选择排序的思想也很容易理解,主要思路就是我们每一趟在 n-i+1 个记录中选取关键字最小的记录作为有序序列的第 i 个记录。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
例如上图,绿色代表已经排序的元素,红色代表未排序的元素。我们当前指针指向 4 ,则我们遍历红色元素,从中找到最小值,然后与 4 交换。我们发现选择排序执行完一次循环也至少可以将 1 个元素归位。
|
|
||||||
|
|
||||||
下面我们来看一下代码的执行过程,看过之后肯定能写出代码的。
|
|
||||||
|
|
||||||
注:我们为了更容易理解,min 值保存的是值,而不是索引,实际代码中保存的是索引
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
**简单选择排序代码**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public int[] sortArray(int[] nums) {
|
|
||||||
|
|
||||||
int len = nums.length;
|
|
||||||
int min = 0;
|
|
||||||
for (int i = 0; i < len; ++i) {
|
|
||||||
min = i;
|
|
||||||
//遍历到最小值
|
|
||||||
for (int j = i + 1; j < len; ++j) {
|
|
||||||
if (nums[min] > nums[j]) min = j;
|
|
||||||
}
|
|
||||||
if (min != i) swap(nums,i,min);
|
|
||||||
}
|
|
||||||
return nums;
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**简单选择排序时间复杂度分析**
|
|
||||||
|
|
||||||
从简单选择排序的过程来看,他最大的特点就是交换移动数据次数相当少,这样也就节省了排序时间,简单选择和冒泡排序不一样,我们发现无论最好情况和最坏情况,元素间的比较次数是一样的,第 i 次排序,需要 n - i 次比较,n 代表数组长度,则一共需要比较(n-1) + (n-2) +.... + 2 + 1= n*(n-1)/2 次,对于交换而言,最好情况交换 0 次,最坏情况(逆序时)交换 n - 1次。那么简单选择排序时间复杂度也为 O(n^2) 但是其交换次数远小于冒泡排序,所以其效率是好于冒泡排序的。
|
|
||||||
|
|
||||||
**简单选择排序空间复杂度分析**
|
|
||||||
|
|
||||||
由我们动图可知,我们的简单选择排序只用到了常量级的额外空间,所以空间复杂度为 O(1)。
|
|
||||||
|
|
||||||
**简单选择排序稳定性分析**
|
|
||||||
|
|
||||||
我们思考一下,我们的简单选择排序是稳定的吗?显然不是稳定的,因为我们需要在指针后面找到最小的值,与指针指向的值交换,见下图。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时我们需要从后面元素中找到最小的元素与指针指向元素交换,也就是元素 2 。但是我们交换后发现,两个相等元素 3 的相对位置发生了改变,所以简单选择排序是不稳定的排序算法。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|
|
||||||
| ------------ | -------------- | -------------- | -------------- | ---------- | -------- |
|
|
||||||
| 简单选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
|
|
||||||
|
|
||||||
@ -1,91 +0,0 @@
|
|||||||
#### 翻转对
|
|
||||||
|
|
||||||
**题目描述**
|
|
||||||
|
|
||||||
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
|
|
||||||
|
|
||||||
你需要返回给定数组中的重要翻转对的数量。
|
|
||||||
|
|
||||||
示例 1:
|
|
||||||
|
|
||||||
> 输入: [1,3,2,3,1]
|
|
||||||
> 输出: 2
|
|
||||||
|
|
||||||
示例 2:
|
|
||||||
|
|
||||||
> 输入: [2,4,3,5,1]
|
|
||||||
> 输出: 3
|
|
||||||
|
|
||||||
**题目解析**
|
|
||||||
|
|
||||||
我们理解了逆序对的含义之后,题目理解起来完全没有压力的,这个题目第一想法可能就是用暴力法解决,但是会超时,所以我们有没有办法利用归并排序来完成呢?
|
|
||||||
|
|
||||||
我们继续回顾一下归并排序的归并过程,两个小集合是有序的,然后我们需要将小集合归并到大集合中,则我们完全可以在归并之前,先统计一下翻转对的个数,然后再进行归并,则最后排序完成之后自然也就得出了翻转对的个数。具体过程见下图。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
此时我们发现 6 > 2 * 2,所以此时是符合情况的,因为小数组是单调递增的,所以 6 后面的元素都符合条件,所以我们 count += mid - temp1 + 1;则我们需要移动紫色指针,判断后面是否还存在符合条件的情况。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
我们此时发现 6 = 3 * 2,不符合情况,因为小数组都是完全有序的,所以我们可以移动红色指针,看下后面的数有没有符合条件的情况。这样我们就可以得到翻转对的数目啦。下面我们直接看动图加深下印象吧!
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
是不是很容易理解啊,那我们直接看代码吧,仅仅是在归并排序的基础上加了几行代码。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
private int count;
|
|
||||||
|
|
||||||
public int reversePairs(int[] nums) {
|
|
||||||
count = 0;
|
|
||||||
merge(nums, 0, nums.length - 1);
|
|
||||||
return count;
|
|
||||||
}
|
|
||||||
|
|
||||||
public void merge(int[] nums, int left, int right) {
|
|
||||||
|
|
||||||
if (left < right) {
|
|
||||||
int mid = left + ((right - left) >> 1);
|
|
||||||
merge(nums, left, mid);
|
|
||||||
merge(nums, mid + 1, right);
|
|
||||||
mergeSort(nums, left, mid, right);
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
|
|
||||||
public void mergeSort(int[] nums, int left, int mid, int right) {
|
|
||||||
|
|
||||||
int[] temparr = new int[right - left + 1];
|
|
||||||
int temp1 = left, temp2 = mid + 1, index = 0;
|
|
||||||
//计算翻转对
|
|
||||||
while (temp1 <= mid && temp2 <= right) {
|
|
||||||
//这里需要防止溢出
|
|
||||||
if (nums[temp1] > 2 * (long) nums[temp2]) {
|
|
||||||
count += mid - temp1 + 1;
|
|
||||||
temp2++;
|
|
||||||
} else {
|
|
||||||
temp1++;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//记得归位,我们还要继续使用
|
|
||||||
temp1 = left;
|
|
||||||
temp2 = mid + 1;
|
|
||||||
//归并排序
|
|
||||||
while (temp1 <= mid && temp2 <= right) {
|
|
||||||
|
|
||||||
if (nums[temp1] <= nums[temp2]) {
|
|
||||||
temparr[index++] = nums[temp1++];
|
|
||||||
} else {
|
|
||||||
temparr[index++] = nums[temp2++];
|
|
||||||
}
|
|
||||||
}
|
|
||||||
//照旧
|
|
||||||
if (temp1 <= mid) System.arraycopy(nums, temp1, temparr, index, mid - temp1 + 1);
|
|
||||||
if (temp2 <= right) System.arraycopy(nums, temp2, temparr, index, right - temp2 + 1);
|
|
||||||
System.arraycopy(temparr, 0, nums, left, right - left + 1);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
@ -1,146 +0,0 @@
|
|||||||
今天我们一起来看一下可以用快速排序秒杀的经典题,或许这些题目大家已经做过,不过可以再来一起复习一遍,加深印象。
|
|
||||||
|
|
||||||
阅读这篇文章之前,大家要先去看一下我之前写过的快速排序,这样才不会对这篇文章一知半解。好啦,我们一起开整吧。
|
|
||||||
|
|
||||||
在上篇文章中,我们提到了,快速排序的优化,利用三向切分来优化数组中存在大量重复元素的情况,到啦这里各位应该猜到我想写什么了吧,
|
|
||||||
|
|
||||||
我们今天先来说一下那个非常经典的荷兰国旗问题。
|
|
||||||
|
|
||||||
> 题目来源:https://www.jianshu.com/p/356604b8903f
|
|
||||||
|
|
||||||
问题描述:
|
|
||||||
|
|
||||||
荷兰国旗是由红白蓝3种颜色的条纹拼接而成,如下图所示:
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
假设这样的条纹有多条,且各种颜色的数量不一,并且随机组成了一个新的图形,新的图形可能如下图所示,但是绝非只有这一种情况:
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
需求是:把这些条纹按照颜色排好,红色的在上半部分,白色的在中间部分,蓝色的在下半部分,我们把这类问题称作荷兰国旗问题。
|
|
||||||
|
|
||||||
我们把荷兰国旗问题用数组的形式表达一下是这样的:
|
|
||||||
|
|
||||||
给定一个整数数组,给定一个值K,这个值在原数组中一定存在,要求把数组中小于 K 的元素放到数组的左边,大于K的元素放到数组的右边,等于K的元素放到数组的中间,最终返回一个整数数组,其中只有两个值,分别是等于K的数组部分的左右两个下标值。
|
|
||||||
|
|
||||||
例如,给定数组:[2, 3, 1, 9, 7, 6, 1, 4, 5],给定一个值4,那么经过处理原数组可能得一种情况是:[2, 3, 1, 1, 4, 9, 7, 6, 5],需要注意的是,小于4的部分不需要有序,大于4的部分也不需要有序,返回等于4部分的左右两个下标,即[4, 4]
|
|
||||||
|
|
||||||
这不就是我们之前说过的三向切分吗?一模一样!
|
|
||||||
|
|
||||||
那么 leetcode 有没有相似问题呢?我们一起来看下面这道题
|
|
||||||
|
|
||||||
**leetcode 75 颜色分类**
|
|
||||||
|
|
||||||
题目描述:
|
|
||||||
|
|
||||||
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
|
|
||||||
|
|
||||||
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
|
|
||||||
|
|
||||||
示例 1:
|
|
||||||
|
|
||||||
> 输入:nums = [2,0,2,1,1,0]
|
|
||||||
> 输出:[0,0,1,1,2,2]
|
|
||||||
|
|
||||||
示例 2:
|
|
||||||
|
|
||||||
> 输入:nums = [2,0,1]
|
|
||||||
> 输出:[0,1,2]
|
|
||||||
|
|
||||||
示例 3:
|
|
||||||
|
|
||||||
> 输入:nums = [0]
|
|
||||||
> 输出:[0]
|
|
||||||
|
|
||||||
示例 4:
|
|
||||||
|
|
||||||
> 输入:nums = [1]
|
|
||||||
> 输出:[1]
|
|
||||||
|
|
||||||
**做题思路**
|
|
||||||
|
|
||||||
这个题目我们使用 Arrays.sort() 解决,哈哈,但是那样太无聊啦,题目含义就是让我们将所有的 0 放在前面,2放在后面,1 放在中间,是不是和我们上面说的荷兰国旗问题一样。我们仅仅将 1 做为 pivot 值。
|
|
||||||
|
|
||||||
下面我们直接看代码吧,和三向切分基本一致。
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public void sortColors(int[] nums) {
|
|
||||||
int len = nums.length;
|
|
||||||
int left = 0;
|
|
||||||
//这里和三向切分不完全一致
|
|
||||||
int i = left;
|
|
||||||
int right = len-1;
|
|
||||||
|
|
||||||
while (i <= right) {
|
|
||||||
if (nums[i] == 2) {
|
|
||||||
swap(nums,i,right--);
|
|
||||||
} else if (nums[i] == 0) {
|
|
||||||
swap(nums,i++,left++);
|
|
||||||
} else {
|
|
||||||
i++;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
}
|
|
||||||
public void swap (int[] nums, int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
另外我们看这段代码,有什么问题呢?那就是我们即使完全符合时,仍会交换元素,这样会大大降低我们的效率。
|
|
||||||
|
|
||||||
例如:[0,0,0,1,1,1,2,2,2]
|
|
||||||
|
|
||||||
此时我们完全符合情况,不需要交换元素,但是按照我们上面的代码,0,2 的每个元素会和自己进行交换,所以这里我们可以根据 i 和 left 的值是否相等来决定是否需要交换,大家可以自己写一下。
|
|
||||||
|
|
||||||
下面我们看一下另外一种写法
|
|
||||||
|
|
||||||
这个题目的关键点就是,当我们 nums[i] 和 nums[right] 交换后,我们的 nums[right] 此时指向的元素是符合要求的,但是我们 nums[i] 指向的元素不一定符合要求,所以我们需要继续判断。
|
|
||||||
|
|
||||||
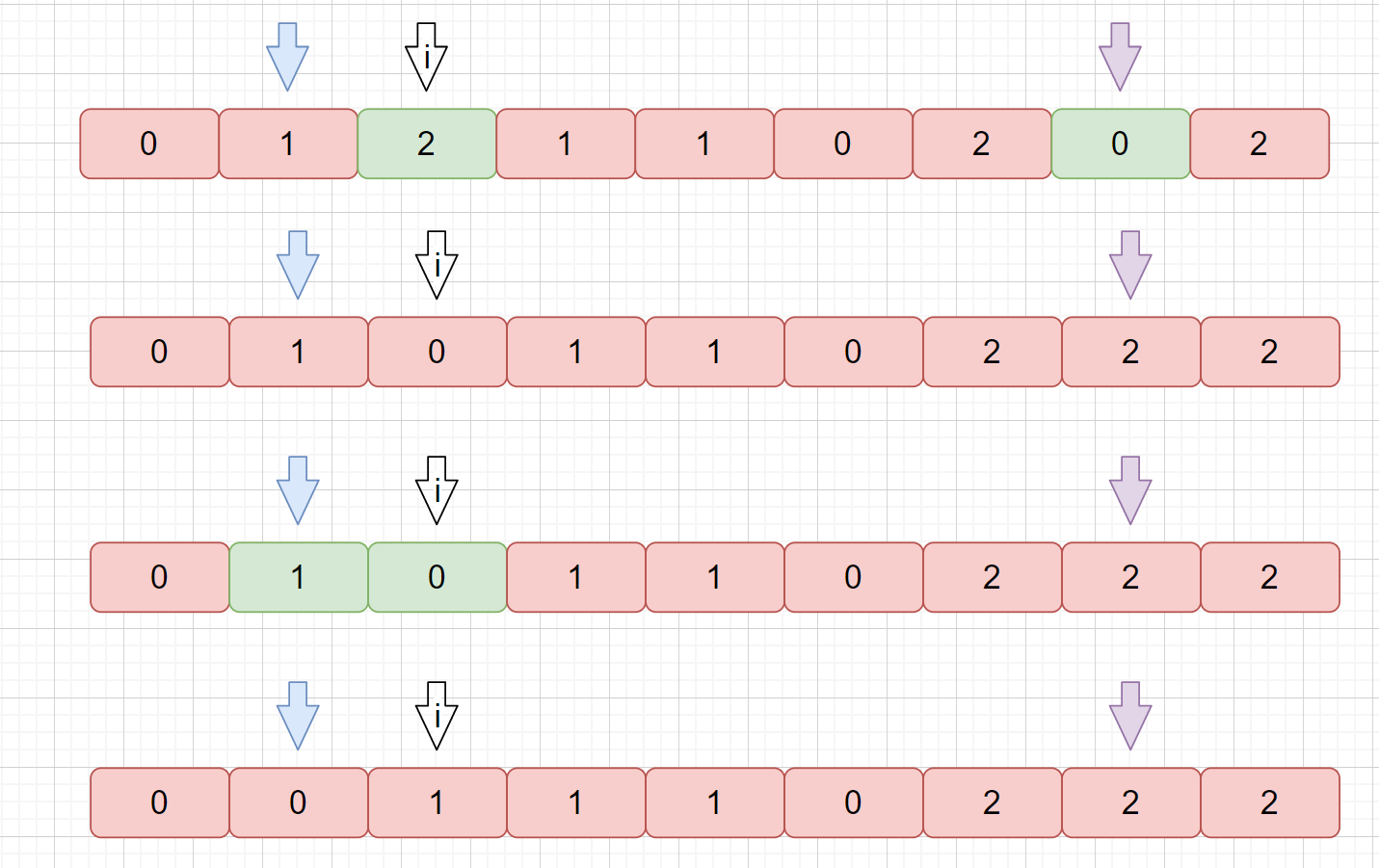
|
|
||||||
|
|
||||||
我们 2 和 0 交换后,此时 i 指向 0 ,0 应放在头部,所以不符合情况,所以 0 和 1 仍需要交换。下面我们来看一下动画来加深理解吧。
|
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
另一种代码表示
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
public void sortColors(int[] nums) {
|
|
||||||
|
|
||||||
int left = 0;
|
|
||||||
int len = nums.length;
|
|
||||||
int right = len - 1;
|
|
||||||
for (int i = 0; i <= right; ++i) {
|
|
||||||
if (nums[i] == 0) {
|
|
||||||
swap(nums,i,left);
|
|
||||||
left++;
|
|
||||||
}
|
|
||||||
if (nums[i] == 2) {
|
|
||||||
swap(nums,i,right);
|
|
||||||
right--;
|
|
||||||
//如果不等于 1 则需要继续判断,所以不移动 i 指针,i--
|
|
||||||
if (nums[i] != 1) {
|
|
||||||
i--;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
public void swap (int[] nums,int i, int j) {
|
|
||||||
int temp = nums[i];
|
|
||||||
nums[i] = nums[j];
|
|
||||||
nums[j] = temp;
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
好啦,这个问题到这就结束啦,是不是很简单啊,我们明天见!
|
|
||||||
|
|
||||||
@ -1,88 +0,0 @@
|
|||||||
#### 逆序对
|
|
||||||
|
|
||||||
逆序对:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对,见下图。
|
|
||||||
|
|
||||||
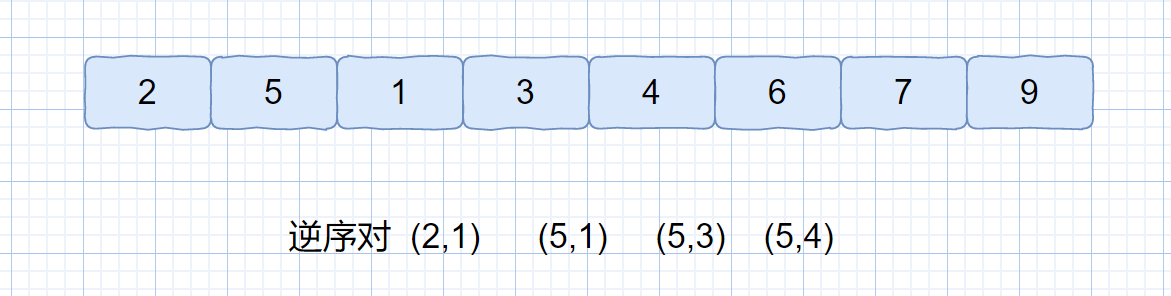
|
|
||||||
|
|
||||||
是不是很容易理解,因为数组是无序的,当较大的数,出现在较小数前面的时候,它俩则可以组成逆序对。因为数组的(有序度+逆序度)= n (n-1) / 2,逆序对个数 = 数组的逆序度,有序对个数 = 数组的有序度,所以我们知道有序对个数的话,也能得到逆序对的个数。另外我们如何通过归并排序来计算逆序对个数呢?
|
|
||||||
|
|
||||||
关键点在我们的**归并过程中**,我们先来看下归并过程中是怎么计算逆序对个数的。见下图
|
|
||||||
|
|
||||||
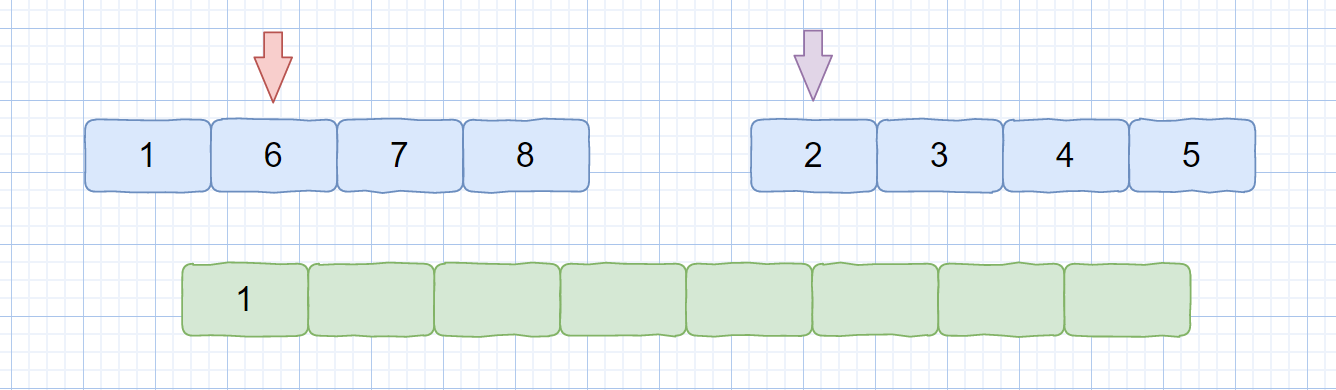
|
|
||||||
|
|
||||||
我们来拆解下上图,我们此时 temp1 指向元素为 6,temp2 指向元素为 2, nums[temp1] > temp[temp2],则此时我们需要将 temp2 指向的元素存入临时数组中,又因为每个小集合中的元素都是有序的,所以 temp1 后面的元素也一定大于 2,那么我们就可以根据 temp1 的索引得出逆序对中包含 2 的逆序对个数,则是 mid - temp + 1。
|
|
||||||
|
|
||||||
好啦这个题目你已经会做啦,下面我们一起来做下吧。
|
|
||||||
|
|
||||||
**题目描述**
|
|
||||||
|
|
||||||
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
|
|
||||||
|
|
||||||
**示例 1:**
|
|
||||||
|
|
||||||
> 输入: [7,5,6,4]
|
|
||||||
> 输出: 5
|
|
||||||
|
|
||||||
**题目解析**
|
|
||||||
|
|
||||||
各位如果忘记归并排序的话,可以再看一下咱们之前的文章回顾一下 [归并排序详解](https://mp.weixin.qq.com/s/YK43J73UNFRjX4r0vh13ZA),这个题目我们仅仅在归并排序的基础上加了一行代码。那就是在归并过程时,nums[temp2] < nums[temp1] 时统计个数。下面我们直接看代码吧。
|
|
||||||
|
|
||||||
**题目代码**
|
|
||||||
|
|
||||||
```java
|
|
||||||
class Solution {
|
|
||||||
//全局变量
|
|
||||||
private int count;
|
|
||||||
public int reversePairs(int[] nums) {
|
|
||||||
count = 0;
|
|
||||||
merge(nums,0,nums.length-1);
|
|
||||||
return count;
|
|
||||||
}
|
|
||||||
|
|
||||||
public void merge (int[] nums, int left, int right) {
|
|
||||||
|
|
||||||
if (left < right) {
|
|
||||||
int mid = left + ((right - left) >> 1);
|
|
||||||
merge(nums,left,mid);
|
|
||||||
merge(nums,mid+1,right);
|
|
||||||
mergeSort(nums,left,mid,right);
|
|
||||||
}
|
|
||||||
|
|
||||||
}
|
|
||||||
|
|
||||||
public void mergeSort(int[] nums, int left, int mid, int right) {
|
|
||||||
|
|
||||||
int[] temparr = new int[right-left+1];
|
|
||||||
int index = 0;
|
|
||||||
int temp1 = left, temp2 = mid+1;
|
|
||||||
|
|
||||||
while (temp1 <= mid && temp2 <= right) {
|
|
||||||
|
|
||||||
if (nums[temp1] <= nums[temp2]) {
|
|
||||||
temparr[index++] = nums[temp1++];
|
|
||||||
} else {
|
|
||||||
//增加的一行代码,用来统计逆序对个数
|
|
||||||
count += (mid - temp1 + 1);
|
|
||||||
temparr[index++] = nums[temp2++];
|
|
||||||
}
|
|
||||||
}
|
|
||||||
|
|
||||||
if (temp1 <= mid) System.arraycopy(nums,temp1,temparr,index,mid-temp1+1);
|
|
||||||
if (temp2 <= right) System.arraycopy(nums,temp2,temparr,index,right-temp2+1);
|
|
||||||
System.arraycopy(temparr,0,nums,left,right-left+1);
|
|
||||||
}
|
|
||||||
}
|
|
||||||
```
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
好啦,这个题目我们就解决啦,哦对,大家也可以顺手去解决下这个题目。leetcode 912 排序数组,这个题目大家可以用来练手,因为有些排序算法是面试高频考点,所以大家可以防止遗忘,多用这个题目进行练习,防止手生。下面则是我写文章时代码的提交情况,冒泡排序怎么优化都会超时,其他排序算法倒是都可以通过。
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
好啦,下面我们继续做一个题目吧,也完全可以用归并排序解决,稍微加了一丢丢代码,但是也是很好理解的。感谢支持
|
|
||||||
|
|
||||||
Loading…
Reference in New Issue
Block a user