ehlxr/algorithm-base
1
0
Fork 0
mirror of https://github.com/chefyuan/algorithm-base.git synced 2024-11-24 13:03:41 +00:00
Code Issues Projects Releases Wiki Activity

test

Browse Source
This commit is contained in:
chefyuan 2021-03-18 09:28:12 +08:00
parent 6879ed51a2
commit 4ca5164ea9
6 changed files with 344 additions and 73 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

90
gif-algorithm/前缀和/leetcode1248寻找优美子数组.md Normal file
View File

@ -0,0 +1,90 @@
### leetcode1248. 统计「优美子数组」
**题目描述**
> 给你一个整数数组 nums 和一个整数 k。
>
> 如果某个 连续 子数组中恰好有 k 个奇数数字，我们就认为这个子数组是「优美子数组」。
>
> 请返回这个数组中「优美子数组」的数目。
**示例 1：**
> 输入：nums = [1,1,2,1,1], k = 3
> 输出：2
> 解释：包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。
**示例 2：**
> 输入：nums = [2,4,6], k = 1
> 输出：0
> 解释：数列中不包含任何奇数，所以不存在优美子数组。
**示例 3：**
> 输入：nums = [2,2,2,1,2,2,1,2,2,2], k = 2
> 输出：16
如果上面那个题目我们完成了，这个题目做起来，分分钟的事，不信你去写一哈，百分百就整出来了，我们继续按上面的思想来解决。
**HashMap**
**解析**
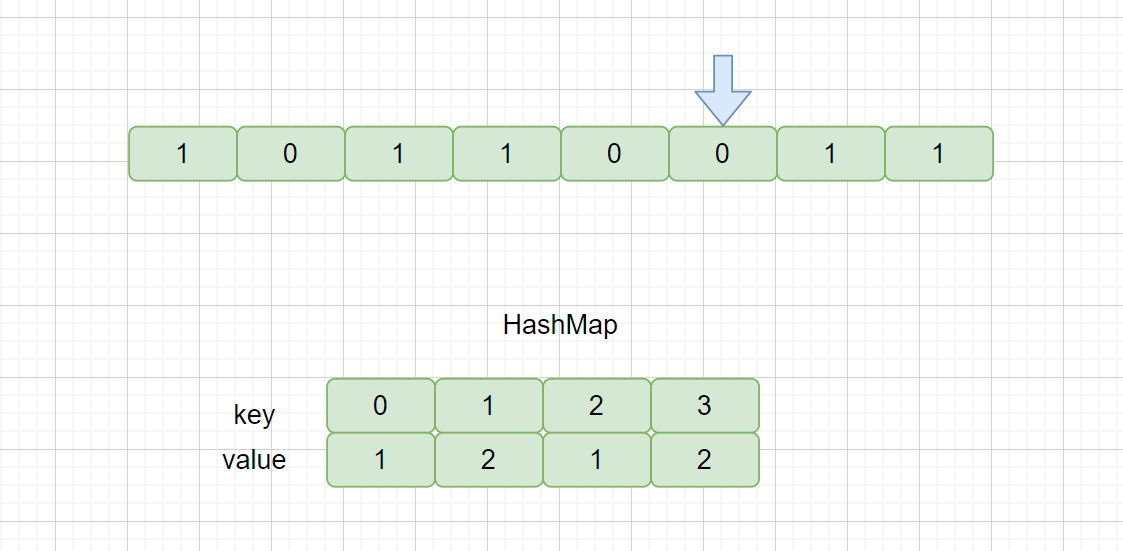
上个题目我们是求和为 K 的子数组，这个题目是让我们求 恰好有 k 个奇数数字的连续子数组，这两个题几乎是一样的，上个题中我们将前缀区间的和保存到哈希表中，这个题目我们只需将前缀区间的奇数个数保存到区间内即可，只不过将 sum += x 改成了判断奇偶的语句，见下图。
![微信截图_20210114222339](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210114222339.c0gwtdh8m94.png)
我们来解析一下哈希表，key 代表的是含有 1 个奇数的前缀区间，value 代表这种子区间的个数，含有两个，也就是nums[0],nums[0,1].后面含义相同，那我们下面直接看代码吧，一下就能读懂。
```java
class Solution {
public int numberOfSubarrays(int[] nums, int k) {
if (nums.length == 0) {
return 0;
}
HashMap<Integer,Integer> map = new HashMap<>();
//统计奇数个数，相当于我们的 presum
int oddnum = 0;
int count = 0;
map.put(0,1);
for (int x : nums) {
// 统计奇数个数
oddnum += x & 1;
// 发现存在，则 count增加
if (map.containsKey(oddnum - k)) {
count += map.get(oddnum - k);
}
//存入
map.put(oddnum,map.getOrDefault(oddnum,0)+1);
}
return count;
}
}
```
但是也有一点不同，就是我们是统计奇数的个数，数组中的奇数个数肯定不会超过原数组的长度，所以这个题目中我们可以用数组来模拟 HashMap ，用数组的索引来模拟 HashMap 的 key，用值来模拟哈希表的 value。下面我们直接看代码吧。
```java
class Solution {
public int numberOfSubarrays(int[] nums, int k) {
int len = nums.length;
int[] map = new int[len + 1];
map[0] = 1;
int oddnum = 0;
int count = 0;
for (int i = 0; i < len; ++i) {
//如果是奇数则加一，偶数加0，相当于没加
oddnum += nums[i] & 1;
if (oddnum - k >= 0) {
count += map[oddnum-k];
}
map[oddnum]++;
}
return count;
}
}
```
###

77
gif-algorithm/前缀和/leetcode724寻找数组的中心索引.md Normal file
View File

@ -0,0 +1,77 @@
今天我们来说一下刷题时经常用到的前缀和思想，前缀和思想和滑动窗口会经常用在求子数组和子串问题上，当我们遇到此类问题时，则应该需要想到此类解题方式，该文章深入浅出描述前缀和思想，读完这个文章就会有属于自己的解题框架，遇到此类问题时就能够轻松应对。
下面我们先来了解一下什么是前缀和。
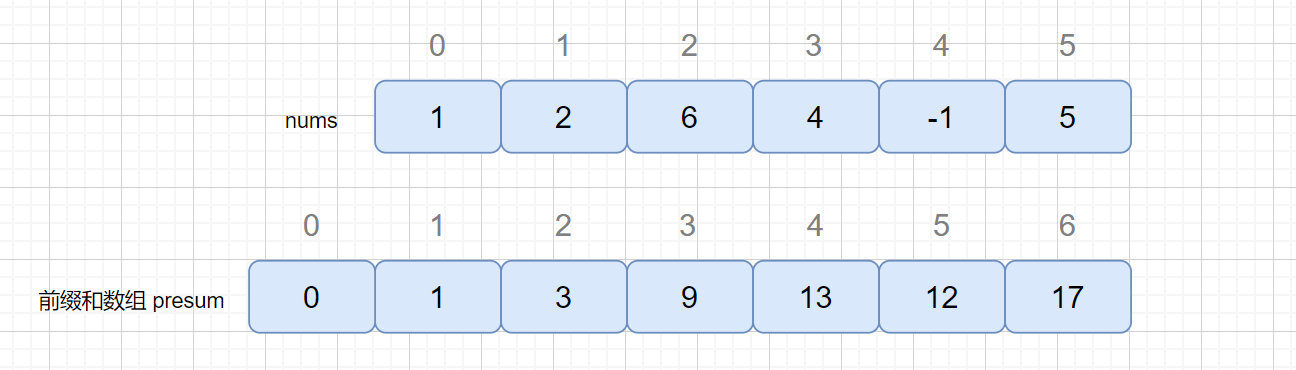
前缀和其实我们很早之前就了解过的，我们求数列的和时，Sn = a1+a2+a3+...an; 此时Sn就是数列的前 n 项和。例 S5 = a1 + a2 + a3 + a4 + a5; S2 = a1 + a2。所以我们完全可以通过 S5-S2 得到 a3+a4+a5 的值，这个过程就和我们做题用到的前缀和思想类似。我们的前缀和数组里保存的就是前 n 项的和。见下图
![](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210113193831.4wk2b9zc8vm0.png)
我们通过前缀和数组保存前 n 位的和，presum[1]保存的就是 nums 数组中前 1 位的和，也就是 **presum[1]** = nums[0], **presum[2]** = nums[0] + nums[1] = **presum[1]** + nums[1]. 依次类推，所以我们通过前缀和数组可以轻松得到每个区间的和。
例如我们需要获取 nums[2] 到 nums[4] 这个区间的和，我们则完全根据 presum 数组得到，是不是有点和我们之前说的字符串匹配算法中 BM,KMP 中的 next 数组和 suffix 数组作用类似。那么我们怎么根据 presum 数组获取 nums[2] 到 nums[4] 区间的和呢？见下图
![前缀和](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/前缀和.77twdj3gpkg0.png)
好啦，我们已经了解了前缀和的解题思想了，我们可以通过下面这段代码得到我们的前缀和数组，非常简单
```java
for (int i = 0; i < nums.length; i++) {
presum[i+1] = nums[i] + presum[i];
}
```
好啦，我们开始实战吧。
### leetcode 724. 寻找数组的中心索引
**题目描述**
> 给定一个整数类型的数组 nums，请编写一个能够返回数组 “中心索引” 的方法。
>
> 我们是这样定义数组 中心索引 的：数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
>
> 如果数组不存在中心索引，那么我们应该返回 -1。如果数组有多个中心索引，那么我们应该返回最靠近左边的那一个。
**示例 1：**
> 输入：
> nums = [1, 7, 3, 6, 5, 6]
> 输出：3
解释：
索引 3 (nums[3] = 6) 的左侧数之和 (1 + 7 + 3 = 11)，与右侧数之和 (5 + 6 = 11) 相等。
同时, 3 也是第一个符合要求的中心索引。
**示例 2：**
> 输入：
> nums = [1, 2, 3]
> 输出：-1
解释：
数组中不存在满足此条件的中心索引。
理解了我们前缀和的概念（不知道好像也可以做，这个题太简单了哈哈）。我们可以一下就能把这个题目做出来，先遍历一遍求出数组的和，然后第二次遍历时，直接进行对比左半部分和右半部分是否相同，如果相同则返回 true，不同则继续遍历。
```java
class Solution {
public int pivotIndex(int[] nums) {
int presum = 0;
//数组的和
for (int x : nums) {
presum += x;
}
int leftsum = 0;
for (int i = 0; i < nums.length; ++i) {
//发现相同情况
if (leftsum == presum - nums[i] - leftsum) {
return i;
}
leftsum += nums[i];
}
return -1;
}
}
```
###

103
gif-algorithm/前缀和/leetcode974和可被K整除的子数组.md Normal file
View File

@ -0,0 +1,103 @@
### leetcode 974 和可被 K 整除的子数组
**题目描述**
> 给定一个整数数组 A，返回其中元素之和可被 K 整除的（连续、非空）子数组的数目。
**示例：**
> 输入：A = [4,5,0,-2,-3,1], K = 5
> 输出：7
**解释：**
> 有 7 个子数组满足其元素之和可被 K = 5 整除：
> [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
**前缀和+HashMap**
**解析**
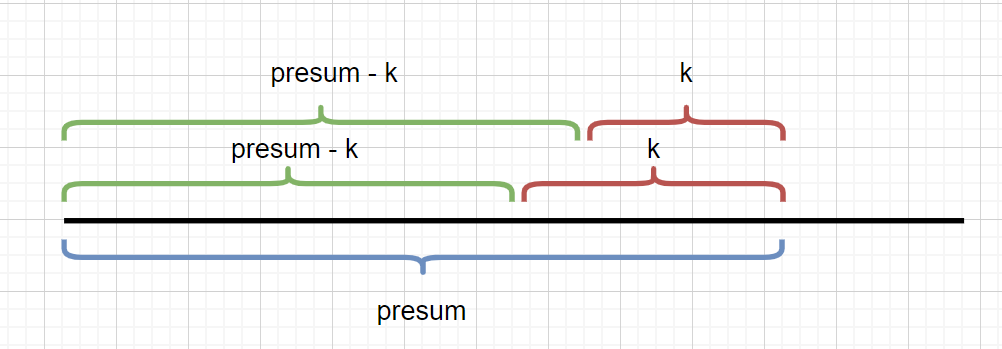
我们在该文的第一题 **和为K的子数组 **中，我们需要求出满足条件的区间，见下图
![微信截图_20210115194113](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210115194113.5e56re9qdic0.png)
我们需要找到满足，和为 K 的区间。我们此时 presum 是已知的，k 也是已知的，我们只需要找到 presum - k区间的个数，就能得到 k 的区间个数。但是我们在当前题目中应该怎么做呢？见下图。
![微信截图_20210115150520](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210115150520.3kh5yiwwmlm0.png)
我们在之前的例子中说到，presum[j+1] - presum[i] 可以得到 nums[i] + nums[i+1]+.... nums[j]，也就是[i,j]区间的和。
那么我们想要判断区间 [i,j] 的和是否能整除 K，也就是上图中紫色那一段是否能整除 K，那么我们只需判断
(presum[j+1] - presum[i] ) % k 是否等于 0 即可，
我们假设 (presum[j+1] - presum[i] ) % k == 0；则
presum[j+1] % k - presum[i] % k == 0;
presum[j +1] % k = presum[i] % k ;
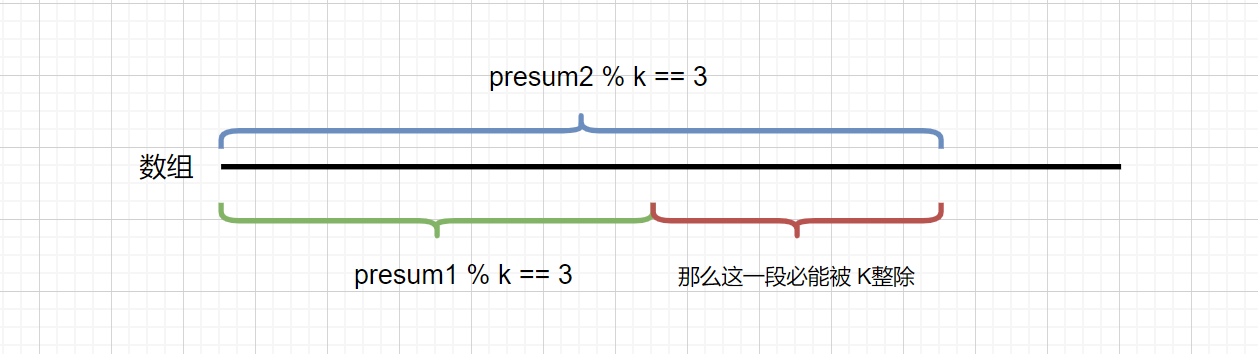
我们 presum[j +1] % k 的值 key 是已知的，则是当前的 presum 和 k 的关系，我们只需要知道之前的前缀区间里含有相同余数 （key）的个数。则能够知道当前能够整除 K 的区间个数。见下图
![微信截图_20210115152113](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210115152113.606bcpexpww0.png)
**题目代码**
```java
class Solution {
public int subarraysDivByK(int[] A, int K) {
HashMap<Integer,Integer> map = new HashMap<>();
map.put(0,1);
int presum = 0;
int count = 0;
for (int x : A) {
presum += x;
//当前 presum 与 K的关系，余数是几，当被除数为负数时取模结果为负数，需要纠正
int key = (presum % K + K) % K;
//查询哈希表获取之前key也就是余数的次数
if (map.containsKey(key)) {
count += map.get(key);
}
//存入哈希表当前key，也就是余数
map.put(key,map.getOrDefault(key,0)+1);
}
return count;
}
}
```
我们看到上面代码中有一段代码是这样的
```java
int key = (presum % K + K) % K;
```
这是为什么呢？不能直接用 presum % k 吗？
这是因为当我们 presum 为负数时，需要对其纠正。纠正前(-1) %2 = (-1)，纠正之后 ( (-1) % 2 + 2) % 2=1 保存在哈希表中的则为 1.则不会漏掉部分情况，例如输入为 [-1,2,9],K = 2如果不对其纠正则会漏掉区间 [2] 此时 2 % 2 = 0，符合条件，但是不会被计数。
那么这个题目我们可不可以用数组，代替 map 呢？当然也是可以的，因为此时我们的哈希表存的是余数，余数最大也只不过是 K-1所以我们可以用固定长度 K 的数组来模拟哈希表。
```java
class Solution {
public int subarraysDivByK(int[] A, int K) {
int[] map = new int[K];
map[0] = 1;
int len = A.length;
int presum = 0;
int count = 0;
for (int i = 0; i < len; ++i) {
presum += A[i];
//求key
int key = (presum % K + K) % K;
//count添加次数，并将当前的map[key]++;
count += map[key]++;
}
return count;
}
}
```

0
gif-algorithm/前缀和/新建文本文档.txt
View File

2
gif-algorithm/数组篇/leetcode560和为K的子数组.md
View File

@ -112,7 +112,7 @@ class Solution {
**动图解析** **动图解析**
![](https://img-blog.csdnimg.cn/2021031809231883.gif#pic_center)
**题目代码** **题目代码**

139
gif-algorithm/数组篇/leetcode75颜色分类.md
View File

@ -1,17 +1,17 @@
### leetcode 75 颜色分类 **leetcode 75 颜色分类**
**题目描述** 题目描述：
> 给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。 给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
>
> 此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
**示例 1：** 此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
示例 1：
> 输入：nums = [2,0,2,1,1,0] > 输入：nums = [2,0,2,1,1,0]
> 输出：[0,0,1,1,2,2] > 输出：[0,0,1,1,2,2]
**示例 2：** 示例 2：
> 输入：nums = [2,0,1] > 输入：nums = [2,0,1]
> 输出：[0,1,2] > 输出：[0,1,2]
@ -26,78 +26,28 @@
> 输入：nums = [1] > 输入：nums = [1]
> 输出：[1] > 输出：[1]
**两次遍历** **做题思路**
**解析：** 这个题目我们使用 Arrays.sort() 解决，哈哈，但是那样太无聊啦，题目含义就是让我们将所有的 0 放在前面，2放在后面，1 放在中间，是不是和我们上面说的荷兰国旗问题一样。我们仅仅将 1 做为 pivot 值。
通过两次遍历，第一遍遍历首先将 0 归位，第二遍遍历将 1 归位，自然 2 也就被归位了，这个方法很容易理解我们直接看代码吧。 下面我们直接看代码吧，和三向切分基本一致。
**题目代码**
```java
class Solution {
public void sortColors(int[] nums) {
int pro = 0;
//将0归位
for (int i = 0; i < nums.length; ++i) {
if (nums[i] == 0) {
swap(nums,i,pro);
pro++;
}
}
//将1归位
for (int j = pro; j < nums.length; ++j) {
if(nums[j] == 1) {
swap(nums,j,pro);
pro++;
}
}
}
public void swap(int[] nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
```
**一次遍历**
**解析**
两次遍历实现是十分容易的，也很容易实现，那么我们可不可以一次遍历就将其归位呢？其实这里也利用了我们双指针的思想，我们首先定义两个指针，一个位于数组头部，一个位于数组尾部，当我们遇到 0 时则给我们头部指针交换，遇到 2 时，则给尾部指针交换。不过里面有两个细节我们需要注意。
1.遍历数组时，指针的上界，不能是 i < nums.length;应是 i <= right;
2.需要注意交换后，当前指针指向的仍不为1。
干看上面两种注意事项，可能不是特别容易理解，我们来看我们的视频解析，就可以搞懂这两个情况啦。
**动图解析**
![leetcode75颜色分类](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/leetcode75颜色分类.5w4sa458rr40.gif)
**题目代码**
```java ```java
class Solution { class Solution {
public void sortColors(int[] nums) { public void sortColors(int[] nums) {
int len = nums.length; int len = nums.length;
int left = 0; int left = 0;
//这里和三向切分不完全一致
int i = left;
int right = len-1; int right = len-1;
//注意看 for 循环的结束条件
for (int i = 0; i <= right; ++i) { while (i <= right) {
if (nums[i] == 0) {
swap(nums,i,left);
left++;
}
if (nums[i] == 2) { if (nums[i] == 2) {
swap(nums,i,right); swap(nums,i,right--);
right--; } else if (nums[i] == 0) {
// 发现此时不为1，则指针不移动，继续交换 swap(nums,i++,left++);
if (nums[i] != 1) { } else {
i--; i++;
}
} }
} }
} }
@ -109,3 +59,54 @@ class Solution {
} }
``` ```
另外我们看这段代码，有什么问题呢？那就是我们即使完全符合时，仍会交换元素，这样会大大降低我们的效率。
例如：[0,0,0,1,1,1,2,2,2]
此时我们完全符合情况，不需要交换元素，但是按照我们上面的代码，0,2 的每个元素会和自己进行交换，所以这里我们可以根据 i 和 left 的值是否相等来决定是否需要交换，大家可以自己写一下。
下面我们看一下另外一种写法
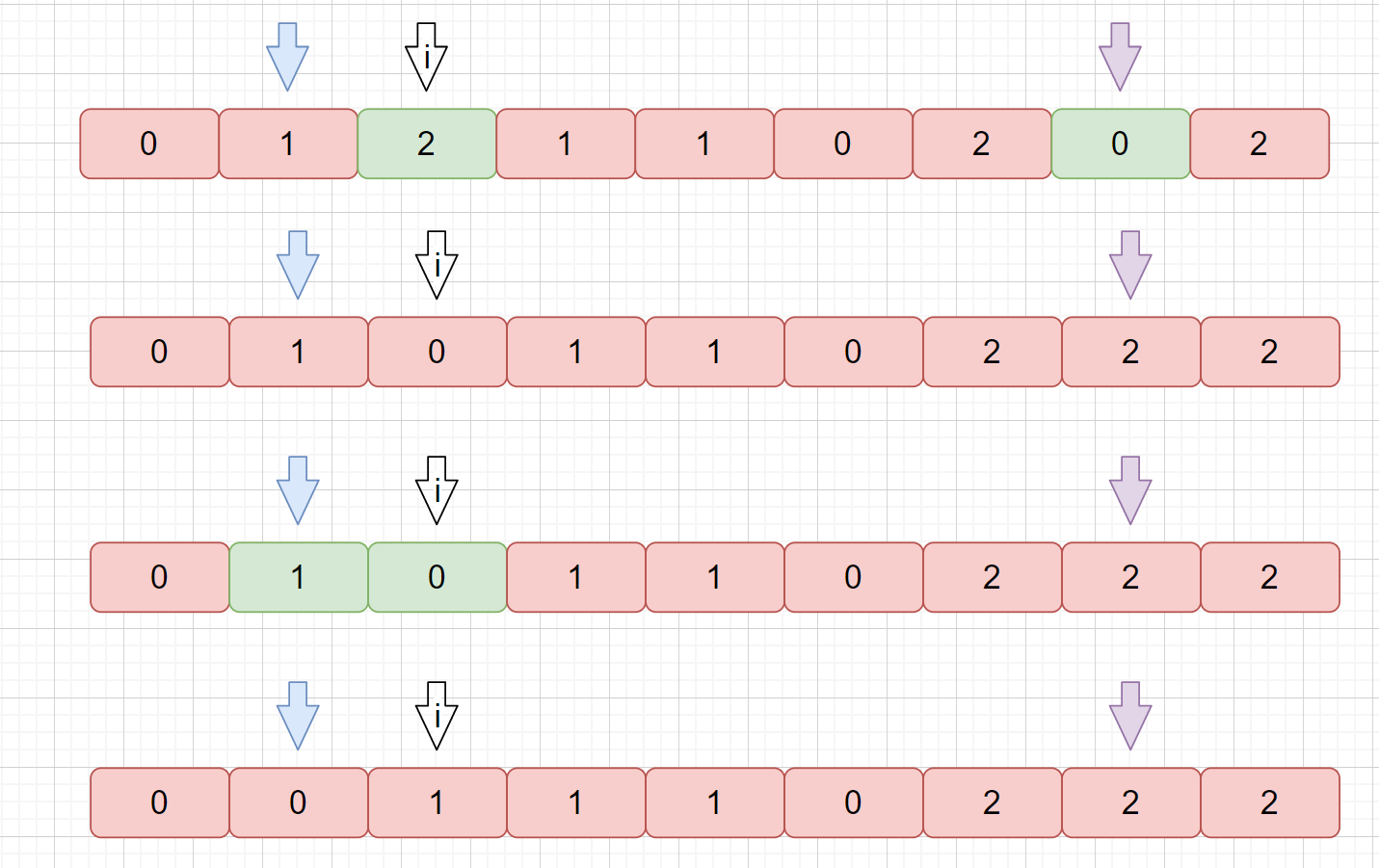
这个题目的关键点就是，当我们 nums[i] 和 nums[right] 交换后，我们的 nums[right] 此时指向的元素是符合要求的，但是我们 nums[i] 指向的元素不一定符合要求，所以我们需要继续判断。
![细节地方](https://cdn.jsdelivr.net/gh/tan45du/test@master/photo/微信截图_20210305153911.28capmzljy80.png)
我们 2 和 0 交换后，此时 i 指向 0 ，0 应放在头部，所以不符合情况，所以 0 和 1 仍需要交换。下面我们来看一下动画来加深理解吧。
![leetcode75颜色分类](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/leetcode75颜色分类.5w4sa458rr40.gif)
另一种代码表示
```java
class Solution {
public void sortColors(int[] nums) {
int left = 0;
int len = nums.length;
int right = len - 1;
for (int i = 0; i <= right; ++i) {
if (nums[i] == 0) {
swap(nums,i,left);
left++;
}
if (nums[i] == 2) {
swap(nums,i,right);
right--;
//如果不等于 1 则需要继续判断，所以不移动 i 指针，i--
if (nums[i] != 1) {
i--;
}
}
}
}
public void swap (int[] nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
```
好啦，这个问题到这就结束啦，是不是很简单啊，我们明天见！