ehlxr/algorithm-base
1
0
Fork 0
mirror of https://github.com/chefyuan/algorithm-base.git synced 2024-12-27 04:46:17 +00:00
Code Issues Projects Releases Wiki Activity

添加了python版本代码

Browse Source 
为数据结构和算法文件夹下的代码增加了python语言版本
This commit is contained in:
goodyong 2021-07-05 22:25:41 +08:00
parent a503e97f11
commit 4e661354d4
16 changed files with 1088 additions and 83 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

56
animation-simulation/数据结构和算法/BF算法.md
View File

@ -68,6 +68,8 @@
#### 题目代码
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -101,10 +103,38 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
haylen = len(haystack)
needlen = len(needle)
# 特殊情况
if haylen < needlen:
return -1
if needlen == 0:
return 0
# 主串
for i in range(0, haylen - needlen + 1):
# 模式串
j = 0
while j < needlen:
if haystack[i + j] != needle[j]:
break
j += 1
# 匹配成功
if j == needlen:
return i
return -1
```
我们看一下BF算法的另一种算法（显示回退），其实原理一样，就是对代码进行了一下修改，只要是看完咱们的动图，这个也能够一下就能看懂，大家可以结合下面代码中的注释和动图进行理解。
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -132,3 +162,29 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
# i代表主串指针，j模式串
i = 0
j = 0
# 主串长度和模式串长度
halen = len(haystack)
nelen = len(needle)
# 循环条件，这里只有 i 增长
while i < halen and j < nelen:
# 相同时，则移动 j 指针
if haystack[i] == needle[j]:
j += 1
else:
# 不匹配时，将 j 重新只想模式串的头部，将 i 本次匹配的开始位置的下一字符
i -= j
j = 0
i += 1
# 查询成功时返回索引，查询失败时返回 -1
renum = i - nelen if j == nelen else -1
return renum
```

85
animation-simulation/数据结构和算法/BM.md
View File

@ -122,6 +122,8 @@ BM 算法是从右往左进行比较，发现坏字符的时候此时 cac 已
这破图画起来是真费劲啊。下面我们来看一下算法代码，代码有点长，我都标上了注释也在网站上 AC 了，如果各位感兴趣可以看一下，不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -215,6 +217,89 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
haylen = len(haystack)
needlen = len(needle)
return self.bm(haystack, haylen, needle, needlen)
# 用来求坏字符情况下移动位数
def badChar(self, b: str, m: int, bc: List[int]):
# 初始化
for i in range(0, 256):
bc[i] = -1
# m 代表模式串的长度，如果有两个 a，则后面那个会覆盖前面那个
for i in range(0, m,):
ascii = ord(b[i])
bc[ascii] = i# 下标
# 用来求好后缀条件下的移动位数
def goodSuffix(self, b: str, m: int, suffix: List[int], prefix: List[bool]):
# 初始化
for i in range(0, m):
suffix[i] = -1
prefix[i] = False
for i in range(0, m - 1):
j = i
k = 0
while j >= 0 and b[j] == b[m - 1 - k]:
j -= 1
k += 1
suffix[k] = j + 1
if j == -1:
prefix[k] = True
def bm(self, a: str, n: int, b: str, m: int)->int:
bc = [0] * 256# 创建一个数组用来保存最右边字符的下标
self.badChar(b, m, bc)
# 用来保存各种长度好后缀的最右位置的数组
suffix_index = [0] * m
# 判断是否是头部，如果是头部则True
ispre = [False] * m
self.goodSuffix(b, m, suffix_index, ispre)
i = 0# 第一个匹配字符
# 注意结束条件
while i <= n - m:
# 从后往前匹配，匹配失败，找到坏字符
j = m - 1
while j >= 0:
if a[i + j] != b[j]:
break
j -= 1
# 模式串遍历完毕，匹配成功
if j < 0:
return i
# 下面为匹配失败时，如何处理
# 求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
x = j - bc[ord(a[i + j])]
y = 0
# 好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
if y < m - 1 and m - 1 - j > 0:
y = self.move(j, m, suffix_index, ispre)
# 移动
i += max(x, y)
return -1
# j代表坏字符的下标
def move(j: int, m: int, suffix_index: List[int], ispre: List[bool])->int:
# 好后缀长度
k = m - 1 - j
# 如果含有长度为 k 的好后缀，返回移动位数
if suffix_index[k] != -1:
return j - suffix_index[k] + 1
# 找头部为好后缀子串的最大长度，从长度最大的子串开始
for r in range(j + 2, m):
# //如果是头部
if ispre[m - r] == True:
return r
# 如果没有发现好后缀匹配的串，或者头部为好后缀子串，则移动到 m 位，也就是匹配串的长度
return m
```
我们来理解一下我们代码中用到的两个数组，因为两个规则的移动位数，只与模式串有关，与主串无关，所以我们可以提前求出每种情况的移动情况，保存到数组中。
![头缀函数](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/头缀函数.145da63ig3s0.png)

60
animation-simulation/数据结构和算法/KMP.md
View File

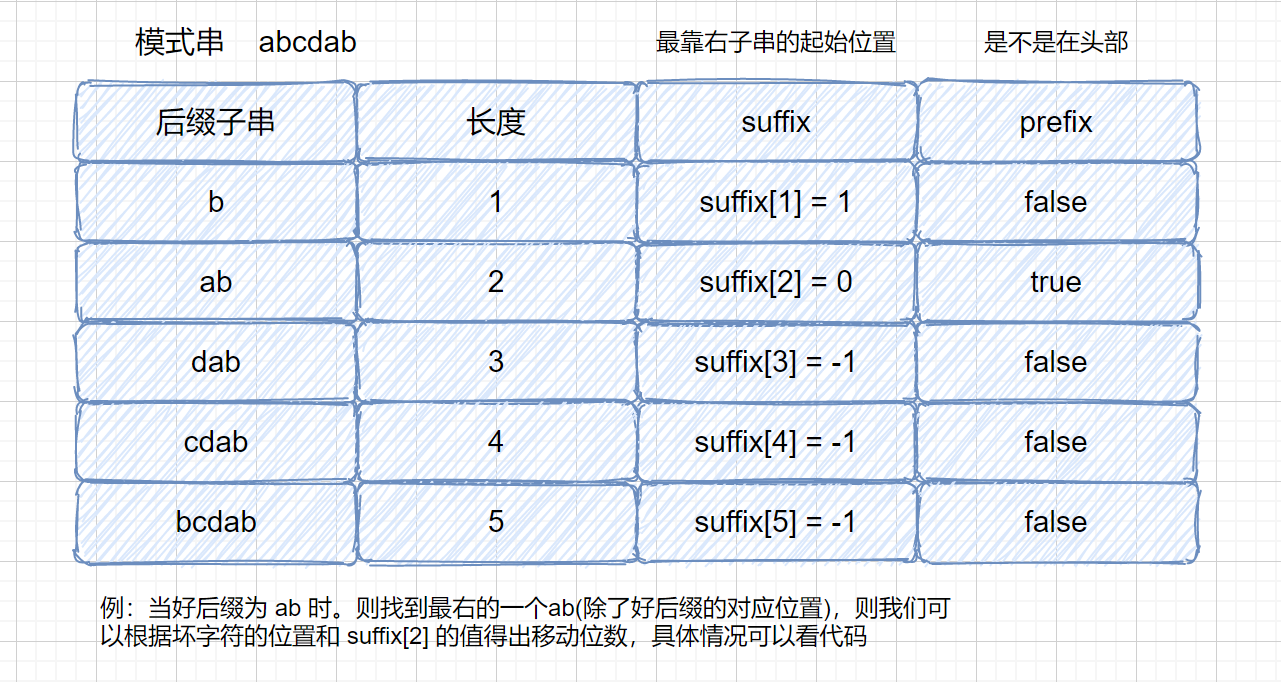
@ -113,7 +113,7 @@ class Solution {
k = next[k];
}
// 相同情况，就是 k的下一位，和 i 相同时，此时我们已经知道 [0,i-1]的最长前后缀
//然后 k - 1 又和 i 相同，最长前后缀加1，即可
//然后 k + 1 又和 i 相同，最长前后缀加1，即可
if (needle[k+1] == needle[i]) {
++k;
}
@ -125,5 +125,63 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
# 两种特殊情况
if len(needle) == 0:
return 0
if len(haystack) == 0:
return -1
# 长度
halen = len(haystack)
nelen = len(needle)
# 返回下标
return self.kmp(haystack, halen, needle, nelen)
def kmp(self, hasyarr: str, halen: int, nearr: str, nelen: int)->int:
# 获取next 数组
next = self.next(nearr, nelen)
j = 0
for i in range(0, halen):
# 发现不匹配的字符，然后根据 next 数组移动指针，移动到最大公共前后缀的，
# 前缀的后一位,和咱们移动模式串的含义相同
while j > 0 and hasyarr[i] != nearr[j]:
j = next[j - 1] + 1
# 超出长度时，可以直接返回不存在
if nelen - j + i > halen:
return -1
# 如果相同就将指针同时后移一下，比较下个字符
if hasyarr[i] == nearr[j]:
j += 1
# 遍历完整个模式串，返回模式串的起点下标
if j == nelen:
return i - nelen + 1
return -1
# 这一块比较难懂，不想看的同学可以忽略，了解大致含义即可，或者自己调试一下，看看运行情况
# 我会每一步都写上注释
def next(self, needle: str, len:int)->List[int]:
# 定义 next 数组
next = [0] * len
# 初始化
next[0] = -1
k = -1
for i in range(1, len):
# 我们此时知道了 [0,i-1]的最长前后缀，但是k+1的指向的值和i不相同时，我们则需要回溯
# 因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标（即长度）
# 就要找 k+1前一个元素在next数组里的值,即next[k+1]
while k != -1 and needle[k + 1] != needle[i]:
k = next[k]
# 相同情况，就是 k的下一位，和 i 相同时，此时我们已经知道 [0,i-1]的最长前后缀
# 然后 k + 1 又和 i 相同，最长前后缀加1，即可
if needle[k + 1] == needle[i]:
k += 1
next[i] = k
return next
```

49
animation-simulation/数据结构和算法/冒泡排序.md
View File

@ -80,6 +80,8 @@
我们来看一下这段代码
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -102,6 +104,25 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
leng = len(nums)
for i in range(0, leng):
for j in range(i + 1, leng):
if nums[i] > nums[j]:
self.swap(nums, i, j)
return nums
def swap(self, nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
```
我们来思考一下上面的代码，每次让关键字 nums[i] 和 nums[j] 进行比较如果 nums[i] > nums[j] 时则进行交换，这样 nums[0] 在经过一次循环后一定为最小值。那么这段代码是冒泡排序吗？
显然不是，我们冒泡排序的思想是两两比较**相邻记录**的关键字，注意里面有相邻记录，所以这段代码不是我们的冒泡排序，下面我们用动图来模拟一下冒泡排序的执行过程，看完之后一定可以写出正宗的冒泡排序。
@ -143,6 +164,8 @@ class Solution {
我们来对冒泡排序进行改进
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -172,6 +195,32 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
leng = len(nums)
# 标志位
flag = True
for i in range(0, leng):
if not flag:
break
flag = False
for j in range(0, leng - i - 1):
if nums[j] > nums[j + 1]:
self.swap(nums, j, j + 1)
# 发生交换，则变为true，下次继续判断
flag = True
return nums
def swap(self, nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
```
这样我们就避免掉了已经有序的情况下无意义的循环判断。
**冒泡排序时间复杂度分析**

57
animation-simulation/数据结构和算法/合成.md
View File

@ -144,6 +144,8 @@ BC < CB 整理得 B / (10 ^ b - 1) < C / (10 ^ c - 1);
好啦，我们证明我们定义的规则有效下面我们直接看代码吧。继续使用我们的三向切分来解决
Java Code:
```java
class Solution {
public String minNumber(int[] nums) {
@ -166,23 +168,23 @@ class Solution {
return;
}
int low = left;
int hight = right;
int high = right;
int i = low+1;
String pivot = arr[low];
while (i <= hight) {
while (i <= high) {
//比较大小
if ((pivot+arr[i]).compareTo(arr[i]+pivot) > 0 ) {
swap(arr,i++,low++);
} else if ((pivot+arr[i]).compareTo(arr[i]+pivot) < 0) {
swap(arr,i,hight--);
swap(arr,i,high--);
} else {
i++;
}
}
quickSort(arr,left,low-1);
quickSort(arr,hight+1,right);
quickSort(arr,high+1,right);
}
public void swap(String[] arr, int i, int j) {
@ -193,6 +195,53 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def minNumber(self, nums: List[int])->str:
arr = [''] * len(nums)
# 解决大数问题，将数字转换为字符串
for i in range(0, len(nums)):
arr[i] = str(nums[i])
self.quickSort(arr, 0, len(arr) - 1)
s = ''
for x in arr:
s += x
return s
def quickSort(self, arr: List[str], left: int, right: int):
if left >= right:
return
low = left
high = right
i = low + 1
pivot = arr[low]
while i <= high:
# 比较大小
if int(pivot + arr[i]) > int(arr[i] + pivot):
self.swap(arr, i, low)
i += 1
low += 1
elif int(pivot + arr[i]) < int(arr[i] + pivot):
self.swap(arr, i, high)
high -= 1
else:
i += 1
self.quickSort(arr, left, low - 1)
self.quickSort(arr, high + 1, right)
def swap(self, arr: List[str], i: int, j: int):
temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
```

75
animation-simulation/数据结构和算法/堆排序.md
View File

@ -3,7 +3,7 @@
> 如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ，备注 github + 题目 + 问题 向我反馈
>
> 感谢支持，该仓库会一直维护，希望对各位有一丢丢帮助。
>
>刷题网站
> 另外希望手机阅读的同学可以来我的 <u>[**公众号：袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
说堆排序之前，我们先简单了解一些什么是堆？堆这种数据结构应用场景非常多，所以我们需要熟练掌握呀！
@ -99,8 +99,10 @@
我们一起来看一下上浮操作代码。
Java Code:
```java
public void swim (int index) {
public void swim (int[] nums, int index) {
while (index > 1 && nums[index/2] > nums[index]) {
swap(index/2,index);//交换
index = index/2;
@ -108,6 +110,15 @@ public void swim (int index) {
}
```
Python Code:
```python
def swim(nums: int, index: int):
while index > 1 and nums[int(index/2)] > nums[index]:
swap(int(index/2), index)# 交换
index = int(index/2)
```
既然利用上浮操作建堆已经搞懂啦，那么我们再来了解一下，利用下沉操作建堆吧，也很容易理解。
给我们一个无序数组（不满足堆的要求），见下图
@ -145,6 +156,8 @@ public void swim (int index) {
好啦我们一起看哈下沉操作的代码吧。
Java Code:
```java
public void sink (int[] nums, int index,int len) {
while (true) {
@ -165,6 +178,24 @@ public void sink (int[] nums, int index,int len) {
}
```
Python Code:
```python
def sink(nums: list, index: int, len: int):
while True:
# 获取子节点
j = 2 * index
if j < len-1 and nums[j] < nums[j+1]:
j += 1
# 交换操作，父节点下沉，与最大的孩子节点交换
if j < len and nums[index] < nums[j]:
swap(nums, index, j)
else:
break
# 继续下沉
index = j
```
好啦，两种建堆方式我们都已经了解啦，那么我们如何进行排序呢？
了解排序之前我们先来，看一下如何删除堆顶元素，我们需要保证的是，删除堆顶元素后，其他元素仍能满足堆的要求，我们思考一下如何实现呢？见下图
@ -187,6 +218,8 @@ public void sink (int[] nums, int index,int len) {
好啦，下面我们一起看代码吧
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -238,6 +271,44 @@ class Solution {
}
```
Python Code:
```python
def sortArray(nums: list)->list:
leng = len(nums)
a = [0] + nums
# 下沉建堆
for i in range(int(leng / 2), 0, -1):
sink(a, i, leng)
k = leng
# 排序
while k > 1:
swap(a, 1, k)
k -= 1
sink(a, 1, k)
for i in range(1, leng + 1):
nums[i - 1] = a[i]
return nums
def swap(nums: list, i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
def sink(nums: list, k: int, end: int):
while 2 * k <= end:
j = 2 * k
if j + 1 <= end and nums[j + 1] > nums[j]:
j += 1
if nums[j] > nums[k]:
swap(nums, j, k)
else:
break
k = j
```
好啦，堆排序我们就到这里啦，是不是搞定啦，总的来说堆排序比其他排序算法稍微难理解一些，重点就是建堆，而且应用比较广泛，大家记得打卡呀。
好啦，我们再来分析一下堆排序的时间复杂度、空间复杂度以及稳定性。

201
animation-simulation/数据结构和算法/字符串匹配算法.md
View File

@ -70,6 +70,8 @@
#### 题目代码
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -103,10 +105,37 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
haylen = len(haystack)
needlen = len(needle)
# 特殊情况
if haylen < needlen:
return -1
if needlen == 0:
return 0
# 主串
for i in range(0, haylen - needlen + 1):
# 模式串
j = 0
while j < needlen:
if haystack[i + j] != needle[j]:
break
j += 1
# 匹配成功
if j == needlen:
return i
return -1
```
我们看一下BF算法的另一种算法（显示回退），其实原理一样，就是对代码进行了一下修改，只要是看完咱们的动图，这个也能够一下就能看懂，大家可以结合下面代码中的注释和动图进行理解。
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -134,6 +163,32 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
# i代表主串指针，j模式串
i = 0
j = 0
# 主串长度和模式串长度
halen = len(haystack)
nelen = len(needle)
# 循环条件，这里只有 i 增长
while i < halen and j < nelen:
# 相同时，则移动 j 指针
if haystack[i] == needle[j]:
j += 1
else:
# 不匹配时，将 j 重新只想模式串的头部，将 i 本次匹配的开始位置的下一字符
i -= j
j = 0
i += 1
# 查询成功时返回索引，查询失败时返回 -1
renum = i - nelen if j == nelen else -1
return renum
```
## BM算法(Boyer-Moore)
@ -262,6 +317,8 @@ BM 算法是从右往左进行比较，发现坏字符的时候此时 cac 已
这破图画起来是真费劲啊。下面我们来看一下算法代码，代码有点长，我都标上了注释也在网站上 AC 了，如果各位感兴趣可以看一下，不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -355,6 +412,89 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
haylen = len(haystack)
needlen = len(needle)
return self.bm(haystack, haylen, needle, needlen)
# 用来求坏字符情况下移动位数
def badChar(self, b: str, m: int, bc: List[int]):
# 初始化
for i in range(0, 256):
bc[i] = -1
# m 代表模式串的长度，如果有两个 a，则后面那个会覆盖前面那个
for i in range(0, m,):
ascii = ord(b[i])
bc[ascii] = i# 下标
# 用来求好后缀条件下的移动位数
def goodSuffix(self, b: str, m: int, suffix: List[int], prefix: List[bool]):
# 初始化
for i in range(0, m):
suffix[i] = -1
prefix[i] = False
for i in range(0, m - 1):
j = i
k = 0
while j >= 0 and b[j] == b[m - 1 - k]:
j -= 1
k += 1
suffix[k] = j + 1
if j == -1:
prefix[k] = True
def bm(self, a: str, n: int, b: str, m: int)->int:
bc = [0] * 256# 创建一个数组用来保存最右边字符的下标
self.badChar(b, m, bc)
# 用来保存各种长度好后缀的最右位置的数组
suffix_index = [0] * m
# 判断是否是头部，如果是头部则True
ispre = [False] * m
self.goodSuffix(b, m, suffix_index, ispre)
i = 0# 第一个匹配字符
# 注意结束条件
while i <= n - m:
# 从后往前匹配，匹配失败，找到坏字符
j = m - 1
while j >= 0:
if a[i + j] != b[j]:
break
j -= 1
# 模式串遍历完毕，匹配成功
if j < 0:
return i
# 下面为匹配失败时，如何处理
# 求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
x = j - bc[ord(a[i + j])]
y = 0
# 好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
if y < m - 1 and m - 1 - j > 0:
y = self.move(j, m, suffix_index, ispre)
# 移动
i += max(x, y)
return -1
# j代表坏字符的下标
def move(j: int, m: int, suffix_index: List[int], ispre: List[bool])->int:
# 好后缀长度
k = m - 1 - j
# 如果含有长度为 k 的好后缀，返回移动位数
if suffix_index[k] != -1:
return j - suffix_index[k] + 1
# 找头部为好后缀子串的最大长度，从长度最大的子串开始
for r in range(j + 2, m):
# //如果是头部
if ispre[m - r] == True:
return r
# 如果没有发现好后缀匹配的串，或者头部为好后缀子串，则移动到 m 位，也就是匹配串的长度
return m
```
我们来理解一下我们代码中用到的两个数组，因为两个规则的移动位数，只与模式串有关，与主串无关，所以我们可以提前求出每种情况的移动情况，保存到数组中。
![头缀函数](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/头缀函数.145da63ig3s0.png)
@ -413,6 +553,8 @@ next 数组存的咱们最长公共前后缀中，前缀的结尾字符下标。
**注：很多教科书的 next 数组表示方式不一致，理解即可**
Java Code:
```java
class Solution {
public int strStr(String haystack, String needle) {
@ -486,5 +628,64 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def strStr(self, haystack: str, needle: str)->int:
# 两种特殊情况
if len(needle) == 0:
return 0
if len(haystack) == 0:
return -1
# 长度
halen = len(haystack)
nelen = len(needle)
# 返回下标
return self.kmp(haystack, halen, needle, nelen)
def kmp(self, hasyarr: str, halen: int, nearr: str, nelen: int)->int:
# 获取next 数组
next = self.next(nearr, nelen)
j = 0
for i in range(0, halen):
# 发现不匹配的字符，然后根据 next 数组移动指针，移动到最大公共前后缀的，
# 前缀的后一位,和咱们移动模式串的含义相同
while j > 0 and hasyarr[i] != nearr[j]:
j = next[j - 1] + 1
# 超出长度时，可以直接返回不存在
if nelen - j + i > halen:
return -1
# 如果相同就将指针同时后移一下，比较下个字符
if hasyarr[i] == nearr[j]:
j += 1
# 遍历完整个模式串，返回模式串的起点下标
if j == nelen:
return i - nelen + 1
return -1
# 这一块比较难懂，不想看的同学可以忽略，了解大致含义即可，或者自己调试一下，看看运行情况
# 我会每一步都写上注释
def next(self, needle: str, len:int)->List[int]:
# 定义 next 数组
next = [0] * len
# 初始化
next[0] = -1
k = -1
for i in range(1, len):
# 我们此时知道了 [0,i-1]的最长前后缀，但是k+1的指向的值和i不相同时，我们则需要回溯
# 因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标（即长度）
# 就要找 k+1前一个元素在next数组里的值,即next[k+1]
while k != -1 and needle[k + 1] != needle[i]:
k = next[k]
# 相同情况，就是 k的下一位，和 i 相同时，此时我们已经知道 [0,i-1]的最长前后缀
# 然后 k - 1 又和 i 相同，最长前后缀加1，即可
if needle[k + 1] == needle[i]:
k += 1
next[i] = k
return next
```
这篇文章真的写了很久很久，觉得还不错的话，就麻烦您点个赞吧，大家也可以去我的公众号看我的所有文章，每个都有动图解析，公众号：[袁厨的算法小屋](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/qrcode_for_gh_1f36d2ef6df9_258.5lojyphpkso0.jpg)

30
animation-simulation/数据结构和算法/希尔排序.md
View File

@ -28,6 +28,8 @@
**希尔排序代码**
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -58,6 +60,34 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
increment = len(nums)
# 注意看结束条件
while increment > 1:
# 这里可以自己设置
increment = int(increment / 2)
# 根据增量分组
for i in range(0, increment):
# 这块是不是有点面熟，回去看看咱们的插入排序
for j in range(i + increment, len(nums), increment):
temp = nums[j]
k = j - increment
while k >= 0:
if temp < nums[k]:
nums[k + increment] = nums[k]
k -= increment
continue
break
nums[k + increment] = temp
return nums
```
我们刚才说，我们的增量可以自己设置的，我们上面的例子是用的希尔增量，下面我们看这个例子，看看使用希尔增量会出现什么问题。
![](https://cdn.jsdelivr.net/gh/tan45du/bedphoto2@master/20210122/微信截图_20210127212901.62c3o3ss6pg0.png)

100
animation-simulation/数据结构和算法/归并排序.md
View File

@ -54,6 +54,8 @@
下面我们看代码吧。
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -90,6 +92,48 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
self.mergeSort(nums, 0, len(nums) - 1)
return nums
def mergeSort(self, arr: List[int], left: int, right: int):
if left < right:
mid = left + ((right - left) >> 1)
self.mergeSort(arr, left, mid)
self.mergeSort(arr, mid + 1, right)
self.merge(arr, left, mid, right)
# 归并
def merge(self, arr: List[int], left: int, mid: int, right: int):
# 第一步，定义一个新的临时数组
temparr = [0] * (right - left + 1)
temp1 = left
temp2 = mid + 1
index = 0
# 对应第二步，比较每个指针指向的值，小的存入大集合
while temp1 <= mid and temp2 <= right:
if arr[temp1] <= arr[temp2]:
temparr[index] = arr[temp1]
index += 1
temp1 += 1
else:
temparr[index] = arr[temp2]
index += 1
temp2 += 1
# 对应第三步，将某一集合的剩余元素存到大集合中
if temp1 <= mid:
temparr[index: index + mid - temp1 + 1] = arr[temp1: temp1 + mid - temp1 + 1]
if temp2 <= right:
temparr[index: index + right - temp2 + 1] = arr[temp2: temp2 + right - temp2 + 1]
# 将大集合的元素复制回原数组
arr[left: left + right- left + 1] = temparr[0: right - left + 1]
```
**归并排序时间复杂度分析**
我们一趟归并，需要将两个小集合的长度放到大集合中，则需要将待排序序列中的所有记录扫描一遍所以时间复杂度为O(n)。归并排序把集合一层一层的折半分组，则由完全二叉树的深度可知，整个排序过程需要进行 logn（向上取整）次,则总的时间复杂度为 O(nlogn)。另外归并排序的执行效率与要排序的原始数组的有序程度无关，所以在最好，最坏，平均情况下时间复杂度均为 O(nlogn) 。虽然归并排序时间复杂度很稳定，但是他的应用范围却不如快速排序广泛，这是因为归并排序不是原地排序算法，空间复杂度不为 O(1)，那么他的空间复杂度为多少呢？
@ -134,6 +178,8 @@ class Solution {
注：递归法和迭代法的 merge函数代码一样。
Java Code:
```java
class Solution {
public int[] sortArray (int[] nums) {
@ -162,7 +208,7 @@ class Solution {
}
public void merge (int[] arr,int left, int mid, int right) {
//第一步，定义一个新的临时数组
int[] temparr = new int[right -left + 1];
int[] temparr = new int[right - left + 1];
int temp1 = left, temp2 = mid + 1;
int index = 0;
//对应第二步，比较每个指针指向的值，小的存入大集合
@ -182,3 +228,55 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
# 代表子集合大小，1，2，4，8，16.....
k = 1
leng = len(nums)
while k < leng:
self.mergePass(nums, k, leng)
k *= 2
print(nums)
return nums
def mergePass(self, array: List[int], k: int, leng: int):
i = 0
while i < leng - 2 * k:
# 归并
self.merge(array, i, i + k - 1, i + 2 * k - 1)
i += 2 * k
# 归并最后两个序列
if i + k < leng:
self.merge(array, i, i + k - 1, leng - 1)
# 归并
def merge(self, arr: List[int], left: int, mid: int, right: int):
# 第一步，定义一个新的临时数组
temparr = [0] * (right - left + 1)
temp1 = left
temp2 = mid + 1
index = 0
# 对应第二步，比较每个指针指向的值，小的存入大集合
while temp1 <= mid and temp2 <= right:
if arr[temp1] <= arr[temp2]:
temparr[index] = arr[temp1]
index += 1
temp1 += 1
else:
temparr[index] = arr[temp2]
index += 1
temp2 += 1
# 对应第三步，将某一集合的剩余元素存到大集合中
if temp1 <= mid:
temparr[index: index + mid - temp1 + 1] = arr[temp1: temp1 + mid - temp1 + 1]
if temp2 <= right:
temparr[index: index + right - temp2 + 1] = arr[temp2: temp2 + right - temp2 + 1]
# 将大集合的元素复制回原数组
arr[left: left + right- left + 1] = temparr[0: right - left + 1]
```

214
animation-simulation/数据结构和算法/快速排序.md
View File

@ -36,7 +36,7 @@
下面我们先来介绍下挖坑填数的分区方法
基本思想是我们首先以序列的第一个元素为基准数，然后将该位置挖坑，下面判断 nums[hight] 是否大于基准数，如果大于则左移 hight 指针，直至找到一个小于基准数的元素，将其填入之前的坑中，则 hight 位置会出现一个新的坑，此时移动 low 指针，找到大于基准数的元素，填入新的坑中。不断迭代直至完成分区。
基本思想是我们首先以序列的第一个元素为基准数，然后将该位置挖坑，下面判断 nums[high] 是否大于基准数，如果大于则左移 high 指针，直至找到一个小于基准数的元素，将其填入之前的坑中，则 high 位置会出现一个新的坑，此时移动 low 指针，找到大于基准数的元素，填入新的坑中。不断迭代直至完成分区。
大家直接看我们的视频模拟吧，一目了然。
@ -46,6 +46,8 @@
是不是很容易就理解啦，下面我们直接看代码吧。
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -54,30 +56,30 @@ class Solution {
return nums;
}
public void quickSort (int[] nums, int low, int hight) {
public void quickSort (int[] nums, int low, int high) {
if (low < hight) {
int index = partition(nums,low,hight);
if (low < high) {
int index = partition(nums,low,high);
quickSort(nums,low,index-1);
quickSort(nums,index+1,hight);
quickSort(nums,index+1,high);
}
}
public int partition (int[] nums, int low, int hight) {
public int partition (int[] nums, int low, int high) {
int pivot = nums[low];
while (low < hight) {
while (low < high) {
//移动hight指针
while (low < hight && nums[hight] >= pivot) {
hight--;
while (low < high && nums[high] >= pivot) {
high--;
}
//填坑
if (low < hight) nums[low] = nums[hight];
while (low < hight && nums[low] <= pivot) {
if (low < high) nums[low] = nums[high];
while (low < high && nums[low] <= pivot) {
low++;
}
//填坑
if (low < hight) nums[hight] = nums[low];
if (low < high) nums[high] = nums[low];
}
//基准数放到合适的位置
nums[low] = pivot;
@ -107,26 +109,26 @@ class Solution {
}
public void quickSort (int[] nums, int low, int hight) {
public void quickSort (int[] nums, int low, int high) {
if (low < hight) {
int index = partition(nums,low,hight);
if (low < high) {
int index = partition(nums,low,high);
quickSort(nums,low,index-1);
quickSort(nums,index+1,hight);
quickSort(nums,index+1,high);
}
}
public int partition (int[] nums, int low, int hight) {
public int partition (int[] nums, int low, int high) {
int pivot = nums[low];
int start = low;
while (low < hight) {
while (low < hight && nums[hight] >= pivot) hight--;
while (low < hight && nums[low] <= pivot) low++;
if (low >= hight) break;
swap(nums, low, hight);
while (low < high) {
while (low < high && nums[high] >= pivot) high--;
while (low < high && nums[low] <= pivot) low++;
if (low >= high) break;
swap(nums, low, high);
}
//基准值归位
swap(nums,start,low);
@ -175,29 +177,29 @@ class Solution {
stack.push(0);
while (!stack.isEmpty()) {
int low = stack.pop();
int hight = stack.pop();
int high = stack.pop();
if (low < hight) {
int index = partition(nums, low, hight);
if (low < high) {
int index = partition(nums, low, high);
stack.push(index - 1);
stack.push(low);
stack.push(hight);
stack.push(high);
stack.push(index + 1);
}
}
return nums;
}
public int partition (int[] nums, int low, int hight) {
public int partition (int[] nums, int low, int high) {
int pivot = nums[low];
int start = low;
while (low < hight) {
while (low < high) {
while (low < hight && nums[hight] >= pivot) hight--;
while (low < hight && nums[low] <= pivot) low++;
if (low >= hight) break;
swap(nums, low, hight);
while (low < high && nums[high] >= pivot) high--;
while (low < high && nums[low] <= pivot) low++;
if (low >= high) break;
swap(nums, low, high);
}
swap(nums,start,low);
return low;
@ -226,13 +228,13 @@ class Solution {
所以我们可以加上这几行代码实现三数取中法。
```java
int mid = low + ((hight-low) >> 1);
if (nums[low] > nums[hight]) swap(nums,low,hight);
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
int mid = low + ((high-low) >> 1);
if (nums[low] > nums[high]) swap(nums,low,high);
if (nums[mid] > nums[high]) swap(nums,mid,high);
if (nums[mid] > nums[low]) swap(nums,mid,low);
```
其含义就是让我们将中间元素放到 nums[low] 位置做为基准值，最大值放到 nums[hight],最小值放到 nums[mid],即 [4,2,3] 经过上面代码处理后，则变成了 [3,2,4].此时我们选取 3 做为基准值，这样也就避免掉了选取最大或最小值做为基准值的情况。
其含义就是让我们将中间元素放到 nums[low] 位置做为基准值，最大值放到 nums[high],最小值放到 nums[mid],即 [4,2,3] 经过上面代码处理后，则变成了 [3,2,4].此时我们选取 3 做为基准值，这样也就避免掉了选取最大或最小值做为基准值的情况。
**三数取中法**
@ -242,28 +244,28 @@ class Solution {
quickSort(nums,0,nums.length-1);
return nums;
}
public void quickSort (int[] nums, int low, int hight) {
if (low < hight) {
int index = partition(nums,low,hight);
public void quickSort (int[] nums, int low, int high) {
if (low < high) {
int index = partition(nums,low,high);
quickSort(nums,low,index-1);
quickSort(nums,index+1,hight);
quickSort(nums,index+1,high);
}
}
public int partition (int[] nums, int low, int hight) {
public int partition (int[] nums, int low, int high) {
//三数取中，大家也可以使用其他方法
int mid = low + ((hight-low) >> 1);
if (nums[low] > nums[hight]) swap(nums,low,hight);
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
int mid = low + ((high-low) >> 1);
if (nums[low] > nums[high]) swap(nums,low,high);
if (nums[mid] > nums[high]) swap(nums,mid,high);
if (nums[mid] > nums[low]) swap(nums,mid,low);
//下面和之前一样，仅仅是多了上面几行代码
int pivot = nums[low];
int start = low;
while (low < hight) {
while (low < hight && nums[hight] >= pivot) hight--;
while (low < hight && nums[low] <= pivot) low++;
if (low >= hight) break;
swap(nums, low, hight);
while (low < high) {
while (low < high && nums[high] >= pivot) high--;
while (low < high && nums[low] <= pivot) low++;
if (low >= high) break;
swap(nums, low, high);
}
swap(nums,start,low);
return low;
@ -291,38 +293,38 @@ class Solution {
return nums;
}
public void quickSort (int[] nums, int low, int hight) {
public void quickSort (int[] nums, int low, int high) {
if (hight - low <= INSERTION_SORT_MAX_LENGTH) {
insertSort(nums,low,hight);
if (high - low <= INSERTION_SORT_MAX_LENGTH) {
insertSort(nums,low,high);
return;
}
int index = partition(nums,low,hight);
int index = partition(nums,low,high);
quickSort(nums,low,index-1);
quickSort(nums,index+1,hight);
quickSort(nums,index+1,high);
}
public int partition (int[] nums, int low, int hight) {
public int partition (int[] nums, int low, int high) {
//三数取中，大家也可以使用其他方法
int mid = low + ((hight-low) >> 1);
if (nums[low] > nums[hight]) swap(nums,low,hight);
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
int mid = low + ((high-low) >> 1);
if (nums[low] > nums[high]) swap(nums,low,high);
if (nums[mid] > nums[high]) swap(nums,mid,high);
if (nums[mid] > nums[low]) swap(nums,mid,low);
int pivot = nums[low];
int start = low;
while (low < hight) {
while (low < hight && nums[hight] >= pivot) hight--;
while (low < hight && nums[low] <= pivot) low++;
if (low >= hight) break;
swap(nums, low, hight);
while (low < high) {
while (low < high && nums[high] >= pivot) high--;
while (low < high && nums[low] <= pivot) low++;
if (low >= high) break;
swap(nums, low, high);
}
swap(nums,start,low);
return low;
}
public void insertSort (int[] nums, int low, int hight) {
public void insertSort (int[] nums, int low, int high) {
for (int i = low+1; i <= hight; ++i) {
for (int i = low+1; i <= high; ++i) {
int temp = nums[i];
int j;
for (j = i-1; j >= 0; --j) {
@ -366,6 +368,8 @@ class Solution {
**三数取中+三向切分+插入排序**
Java Code:
```java
class Solution {
private static final int INSERTION_SORT_MAX_LENGTH = 7;
@ -374,19 +378,19 @@ class Solution {
return nums;
}
public void quickSort(int nums[], int low, int hight) {
public void quickSort(int nums[], int low, int high) {
//插入排序
if (hight - low <= INSERTION_SORT_MAX_LENGTH) {
insertSort(nums,low,hight);
if (high - low <= INSERTION_SORT_MAX_LENGTH) {
insertSort(nums,low,high);
return;
}
//三数取中
int mid = low + ((hight-low) >> 1);
if (nums[low] > nums[hight]) swap(nums,low,hight);
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
int mid = low + ((high-low) >> 1);
if (nums[low] > nums[high]) swap(nums,low,high);
if (nums[mid] > nums[high]) swap(nums,mid,high);
if (nums[mid] > nums[low]) swap(nums,mid,low);
//三向切分
int left = low, i = low + 1, right = hight;
int left = low, i = low + 1, right = high;
int pvoit = nums[low];
while (i <= right) {
if (pvoit < nums[i]) {
@ -401,11 +405,11 @@ class Solution {
}
}
quickSort(nums,low,left-1);
quickSort(nums,right+1,hight);
quickSort(nums,right+1,high);
}
public void insertSort (int[] nums, int low, int hight) {
public void insertSort (int[] nums, int low, int high) {
for (int i = low+1; i <= hight; ++i) {
for (int i = low+1; i <= high; ++i) {
int temp = nums[i];
int j;
for (j = i-1; j >= 0; --j) {
@ -426,5 +430,65 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
INSERTION_SORT_MAX_LENGTH = 7
def sortArray(self, nums: List[int])->List[int]:
self.quickSort(nums, 0, len(nums) - 1)
return nums
def quickSort(self, nums: List[int], low: int, high: int):
# 插入排序
if high - low <= self.INSERTION_SORT_MAX_LENGTH:
self.insertSort(nums, low, high)
return
# 三数取中
mid = low + ((high - low) >> 1)
if nums[low] > nums[high]:
self.swap(nums, low, high)
if nums[mid] > nums[high]:
self.swap(nums, mid, high)
if nums[mid] > nums[low]:
self. swap(nums, mid, low)
# 三向切分
left = low
i = low + 1
right = high
pivot = nums[low]
while i <= right:
if pivot < nums[i]:
self.swap(nums, i, right)
right -= 1
elif pivot == nums[i]:
i += 1
else:
self.swap(nums, left, i)
left += 1
i += 1
self.quickSort(nums, low, left - 1)
self.quickSort(nums, right + 1, high)
def insertSort(self, nums: List[int], low: int, high: int):
for i in range(low + 1, high + 1):
temp = nums[i]
j = i - 1
while j >= 0:
if temp < nums[j]:
nums[j + 1] = nums[j]
j -= 1
continue
break
nums[j + 1] = temp
def swap(self, nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
```
好啦，一些常用的优化方法都整理出来啦，还有一些其他的优化算法九数取中，优化递归操作等就不在这里进行描述啦，感兴趣的可以自己看一下。好啦，这期的文章就到这里啦，我们下期见，拜了个拜。

27
animation-simulation/数据结构和算法/直接插入排序.md
View File

@ -22,6 +22,8 @@
**直接插入排序代码**
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -48,6 +50,31 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
# 注意 i 的初始值为 1 ，也就是第二个元素开始
for i in range(1, len(nums)):
# 待排序的值
temp = nums[i]
# 需要注意
j = i - 1
while j >= 0:
# 找到合适位置
if temp < nums[j]:
nums[j + 1] = nums[j]
j -= 1
continue
# 跳出循环
break
# 插入到合适位置，这也就是我们没有在循环内定义变量的原因
nums[j + 1] = temp
return nums
```
**直接插入排序时间复杂度分析**
最好情况时，也就是有序的时候，我们不需要移动元素，每次只需要比较一次即可找到插入位置，那么最好情况时的时间复杂度为O(n)。

25
animation-simulation/数据结构和算法/简单选择排序.md
View File

@ -22,6 +22,8 @@
**简单选择排序代码**
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -46,6 +48,29 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
leng = len(nums)
min = 0
for i in range(0, leng):
min = i
# 遍历到最小值
for j in range(i + 1, leng):
if nums[min] > nums[j]:
min = j
if min != i:
self.swap(nums, i, min)
return nums
def swap(self, nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
```
**简单选择排序时间复杂度分析**

55
animation-simulation/数据结构和算法/翻转对.md
View File

@ -40,6 +40,8 @@
是不是很容易理解啊，那我们直接看代码吧，仅仅是在归并排序的基础上加了几行代码。
Java Code:
```java
class Solution {
private int count;
@ -95,3 +97,56 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
count = 0
def reversePairs(self, nums: List[int])->int:
self.count = 0
self.merge(nums, 0, len(nums) - 1)
return self.count
def merge(self, nums: List[int], left: int, right: int):
if left < right:
mid = left + ((right - left) >> 1)
self.merge(nums, left, mid)
self.merge(nums, mid + 1, right)
self.mergeSort(nums, left, mid, right)
def mergeSort(self, nums: List[int], left: int, mid: int, right: int):
temparr = [0] * (right - left + 1)
temp1 = left
temp2 = mid + 1
index = 0
while temp1 <= mid and temp2 <= right:
# 这里需要防止溢出
if nums[temp1] > 2 * nums[temp2]:
self.count += mid - temp1 + 1
temp2 += 1
else:
temp1 += 1
# 记得归位，我们还要继续使用
temp1 = left
temp2 = mid + 1
# 归并排序
while temp1 <= mid and temp2 <= right:
if nums[temp1] <= nums[temp2]:
temparr[index] = nums[temp1]
index += 1
temp1 += 1
else:
temparr[index] = nums[temp2]
index += 1
temp2 += 1
# 照旧
if temp1 <= mid:
temparr[index: index + mid - temp1 + 1] = nums[temp1: temp1 + mid - temp1 + 1]
if temp2 <= right:
temparr[index: index + right - temp2 + 1] = nums[temp2: temp2 + right - temp2 + 1]
nums[left: left + right- left + 1] = temparr[0: right - left + 1]
```

51
animation-simulation/数据结构和算法/荷兰国旗.md
View File

@ -132,6 +132,33 @@ public:
};
```
Python Code:
```python
from typing import List
class Solution:
def sortColors(self, nums: List[int]):
leng = len(nums)
left = 0
# 这里和三向切分不完全一致
i = left
right = leng - 1
while i <= right:
if nums[i] == 2:
self.swap(nums, i, right)
right -= 1
elif nums[i] == 0:
self.swap(nums, i, left)
i += 1
left += 1
else:
i += 1
def swap(self, nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
```
另外我们看这段代码，有什么问题呢？那就是我们即使完全符合时，仍会交换元素，这样会大大降低我们的效率。
例如：[0,0,0,1,1,1,2,2,2]
@ -216,5 +243,29 @@ public:
};
```
```python
from typing import List
class Solution:
def sortColors(self, nums: List[int]):
left = 0
leng = len(nums)
right = leng - 1
for i in range(0, right + 1):
if nums[i] == 0:
self.swap(nums, i, left)
left += 1
if nums[i] == 2:
swap(nums, i, right)
right -= 1
# 如果不等于 1 则需要继续判断，所以不移动 i 指针，i--
if nums[i] != 1:
i -= 1
def swap(nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
```
好啦，这个问题到这就结束啦，是不是很简单啊，我们明天见！

40
animation-simulation/数据结构和算法/计数排序.md
View File

@ -128,6 +128,8 @@ temp[8] = 5。然后再将 presum[5] 减 1 。
一样可以，哦了，到这里我们就搞定了计数排序，下面我们来看一哈代码吧。
Java Code:
```java
class Solution {
public int[] sortArray(int[] nums) {
@ -169,6 +171,44 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
def sortArray(self,nums: List[int])->List[int]:
leng = len(nums)
if leng < 1:
return nums
# 求出最大最小值
max = nums[0]
min = nums[0]
for x in nums:
if max < x:
max = x
if min > x:
min = x
# 设置 presum 数组长度,然后求出我们的前缀和数组，
# 这里我们可以把求次数数组和前缀和数组用一个数组处理
presum = [0] * (max - min + 1)
for x in nums:
presum[x - min] += 1
for i in range(1, len(presum)):
presum[i] = presum[i - 1] + presum[i]
# 临时数组
temp = [0] * leng
# 遍历数组，开始排序，注意偏移量
for i in range(leng - 1, -1, -1):
# 查找 presum 字典，然后将其放到临时数组，注意偏移度
index = presum[nums[i] - min] - 1
temp[index] = nums[i]
# 相应位置减一
presum[nums[i] - min] -= 1
# copy回原数组
nums = temp
return nums
```
好啦，这个排序算法我们已经搞定了，下面我们来扒一扒它。
**计数排序时间复杂度分析**

46
animation-simulation/数据结构和算法/逆序对问题.md
View File

@ -35,6 +35,8 @@
**题目代码**
Java Code:
```java
class Solution {
//全局变量
@ -80,7 +82,51 @@ class Solution {
}
```
Python Code:
```python
from typing import List
class Solution:
count = 0
def reversePairs(self, nums: List[int])->int:
self.count = 0
self.mergeSort(nums, 0, len(nums) - 1)
return self.count
def mergeSort(self, arr: List[int], left: int, right: int):
if left < right:
mid = left + ((right - left) >> 1)
self.mergeSort(arr, left, mid)
self.mergeSort(arr, mid + 1, right)
self.merge(arr, left, mid, right)
# 归并
def merge(self, arr: List[int], left: int, mid: int, right: int):
# 第一步，定义一个新的临时数组
temparr = [0] * (right - left + 1)
temp1 = left
temp2 = mid + 1
index = 0
# 对应第二步，比较每个指针指向的值，小的存入大集合
while temp1 <= mid and temp2 <= right:
if arr[temp1] <= arr[temp2]:
temparr[index] = arr[temp1]
index += 1
temp1 += 1
else:
self.count += (mid - temp1 + 1)
temparr[index] = arr[temp2]
index += 1
temp2 += 1
# 对应第三步，将某一集合的剩余元素存到大集合中
if temp1 <= mid:
temparr[index: index + mid - temp1 + 1] = arr[temp1: temp1 + mid - temp1 + 1]
if temp2 <= right:
temparr[index: index + right - temp2 + 1] = arr[temp2: temp2 + right - temp2 + 1]
# 将大集合的元素复制回原数组
arr[left: left + right- left + 1] = temparr[0: right - left + 1]
```
好啦，这个题目我们就解决啦，哦对，大家也可以顺手去解决下这个题目。leetcode 912 排序数组，这个题目大家可以用来练手，因为有些排序算法是面试高频考点，所以大家可以防止遗忘，多用这个题目进行练习，防止手生。下面则是我写文章时代码的提交情况，冒泡排序怎么优化都会超时，其他排序算法倒是都可以通过。