数组

gif-algorithm/数组篇/leetcode1052爱生气的书店老板.md

@@ -0,0 +1,72 @@
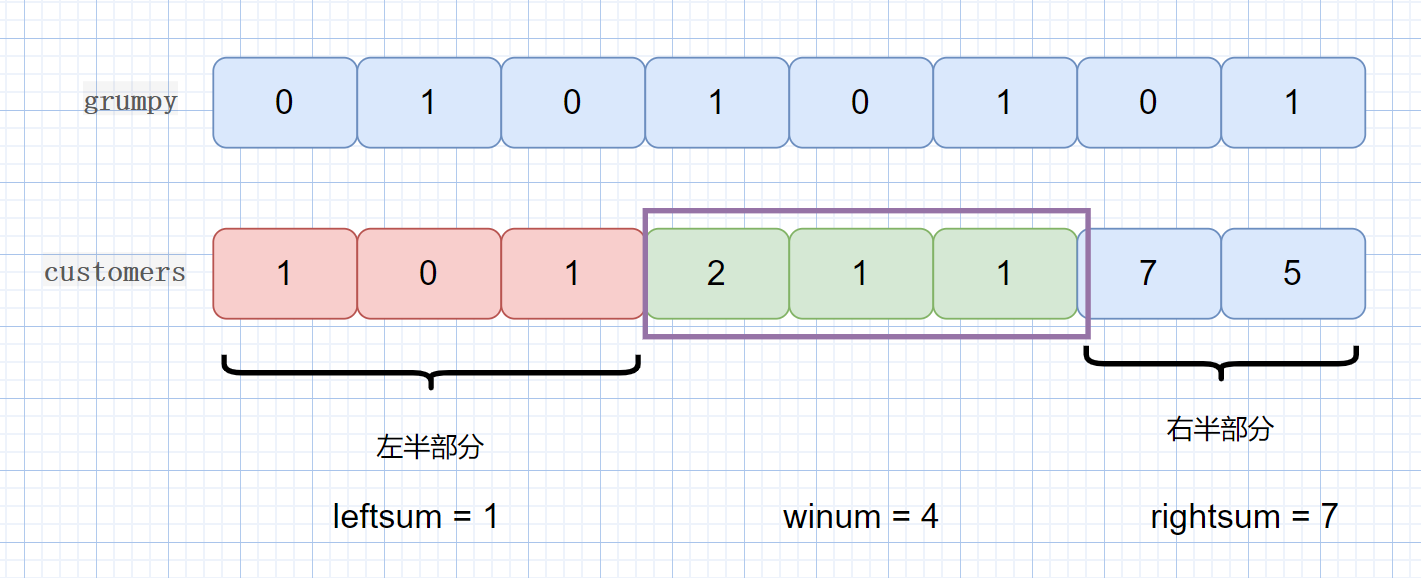
+该题目思想就是，我们将 customer 数组的值分为三部分， leftsum, winsum, rightsum。我们题目的返回值则是三部分的最大和。
+
+注意这里的最大和，我们是怎么计算的。
+
+![](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/微信截图_20210223083057.1vns7wrs2z0.png)
+
+winsum 是窗口内的所有值，不管 grumpy[i] 的值是 0 还是 1,窗口的大小，就对应 K 的值，也就是老板的技能发动时间，该时间段内，老板不会生气，所以为所有的值。
+
+leftsum 是窗口左边区间的值，此时我们不能为所有值，只能是 grumpy[i] == 0 时才可以加入，因为此时不是技能发动期，老板只有在 grumpy[i] == 0 时，才不会生气。
+
+rightsum 是窗口右区间的值，和左区间加和方式一样。那么我们易懂一下窗口，我们的 win 值和 leftsum 值，rightsum 值是怎么变化的呢？
+
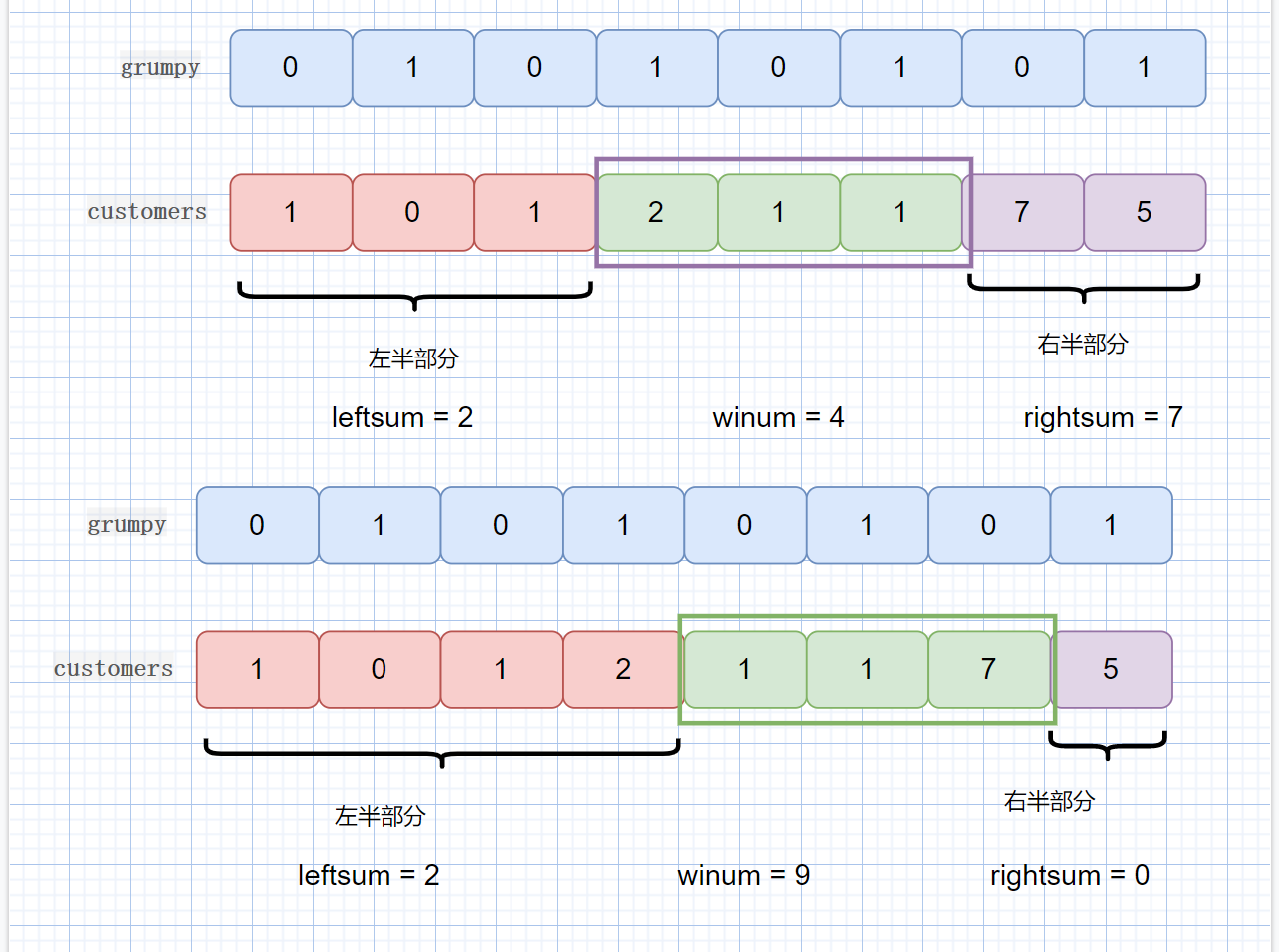
+见下图
+
+![](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/微信截图_20210223084549.5ht4nytfe1o0.png)
+
+我们此时移动了窗口，
+
+则左半区间范围扩大，但是 leftsum 的值没有变，这时因为新加入的值，所对应的 grumpy[i] == 1，所以其值不会发生改变，因为我们只统计 grumpy[i] == 0 的值， 
+
+右半区间范围减少，rightsum 值也减少，因为右半区间减小的值，其对应的 grumpy[i] == 0，所以 rightsum -=  grumpy[i]。
+
+winsum 也会发生变化， winsum 需要加上新加入窗口的值，减去刚离开窗口的值, 也就是 customer[left-1]，left 代表窗口左边缘。
+
+好啦，知道怎么做了，我们直接开整吧。
+
+```java
+class Solution {
+    public int maxSatisfied(int[] customers, int[] grumpy, int X) {
+
+        int winsum = 0;
+        int rightsum = 0;
+        int len = customers.length;
+        //右区间的值
+        for (int i = X; i < len; ++i) {
+            if (grumpy[i] == 0) {
+                rightsum += customers[i];
+            }
+        }
+        //窗口的值
+        for (int i = 0; i < X; ++i) {        
+              winsum += customers[i];          
+        }
+        int leftsum = 0;
+        //窗口左边缘
+        int left = 1;
+        //窗口右边缘
+        int right = X;
+        int maxcustomer = winsum + leftsum + rightsum;     
+        while (right < customers.length) {
+            //重新计算左区间的值，也可以用 customer 值和 grumpy 值相乘获得
+            if (grumpy[left-1] == 0) {
+                leftsum += customers[left-1];
+            }
+            //重新计算右区间值
+            if (grumpy[right] == 0) {
+                rightsum -= customers[right];
+            }
+            //窗口值
+            winsum = winsum - customers[left-1] + customers[right];
+            //保留最大值
+            maxcustomer = Math.max(maxcustomer,winsum+leftsum+rightsum);
+            //移动窗口
+            left++;
+            right++;
+        }        
+        return maxcustomer;
+    }
+}
+```
+
+ 

gif-algorithm/数组篇/leetcode1438绝对值不超过限制的最长子数组.md

@@ -0,0 +1,75 @@
+#### 1438. 绝对差不超过限制的最长连续子数组
+
+给你一个整数数组 nums ，和一个表示限制的整数 limit，请你返回最长连续子数组的长度，该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
+
+如果不存在满足条件的子数组，则返回 0 。
+
+示例
+
+> 输入：nums = [10,1,2,4,7,2], limit = 5
+> 输出：4 
+> 解释：满足题意的最长子数组是 [2,4,7,2]，其最大绝对差 |2-7| = 5 <= 5 。
+
+**提示：**
+
+- 1 <= nums.length <= 10^5
+
+- 1 <= nums[i] <= 10^9
+- 0 <= limit <= 10^9
+
+**题目解析**
+
+我们结合题目，示例，提示来看，这个题目也可以使用滑动窗口的思想来解决。我们需要判断某个子数组是否满足最大绝对差不超过限制值。
+
+那么我们应该怎么解决呢？
+
+我们想一下，窗口内的最大绝对差，如果我们知道窗口的最大值和最小值，最大值减去最小值就能得到最大绝对差。
+
+所以我们这个问题就变成了获取滑动窗口内的最大值和最小值问题，哦？滑动窗口的最大值，是不是很熟悉，大家可以先看一下[滑动窗口的最大值](https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/solution/yi-shi-pin-sheng-qian-yan-shuang-duan-du-mbga/)这个题目，那我们完全可以借助刚才题目的思想来解决这个题目。啪的一下我就搞懂了。
+
+滑动窗口的最大值，我们当时借助了双端队列，来维护一个单调递减的双端队列，进而得到滑动窗口的最大值
+
+那么我们同样可以借助双端队列，来维护一个单调递增的双端队列，来获取滑动窗口的最小值。既然知道了最大值和最小值，我们就可以判断当前窗口是否符合要求，如果符合要求则扩大窗口，不符合要求则缩小窗口，循环结束返回最大的窗口值即可。
+
+下面我们来看一下我们的动画模拟，一下就能看懂！
+
+
+
+
+
+其实，我们只要把握两个重点即可，我们的 maxdeque 维护的是一个单调递减的双端队列，头部为当前窗口的最大值， mindeque 维护的是一个单调递增的双端队列，头部为窗口的最小值，即可。好啦我们一起看代码吧。
+
+```java
+class Solution {
+    public int longestSubarray(int[] nums, int limit) {
+      
+        Deque<Integer> maxdeque = new LinkedList<>();
+        Deque<Integer> mindeque = new LinkedList<>();
+        int len = nums.length;
+        int right = 0, left = 0, maxwin = 0;
+
+        while (right < len) {
+             while (!maxdeque.isEmpty() && maxdeque.peekLast() < nums[right]) {
+                  maxdeque.removeLast();
+             }
+             while (!mindeque.isEmpty() && mindeque.peekLast() > nums[right]) {
+                  mindeque.removeLast();
+             }
+             //需要更多视频解算法，可以来我的公众号：袁厨的算法小屋
+             maxdeque.addLast(nums[right]);
+             mindeque.addLast(nums[right]);                        
+             while (maxdeque.peekFirst() - mindeque.peekFirst() > limit) {
+                if (maxdeque.peekFirst() == nums[left]) maxdeque.removeFirst();
+                if (mindeque.peekFirst() == nums[left]) mindeque.removeFirst();
+                 left++;
+             }
+             //保留最大窗口
+             maxwin = Math.max(maxwin,right-left+1);
+             right++;
+        }
+        return maxwin;
+    }
+}
+```
+
+是不是很有趣这个题目，大家快来打卡吧，希望对各位有一丢丢帮助吧。

gif-algorithm/数组篇/leetcode219数组中重复元素2.md

@@ -0,0 +1,87 @@
+### leetcode 219 数组中重复元素2
+
+**题目描述**
+
+给定一个整数数组和一个整数 k，判断数组中是否存在两个不同的索引 i 和 j，使得 nums [i] = nums [j]，并且 i 和 j 的差的 绝对值 至多为 k。
+
+示例 1:
+
+> 输入: nums = [1,2,3,1], k = 3
+> 输出: true
+
+示例 2:
+
+> 输入: nums = [1,0,1,1], k = 1
+> 输出: true
+
+示例 3:
+
+> 输入: nums = [1,2,3,1,2,3], k = 2
+> 输出: false
+
+**Hashmap**
+
+这个题目和我们上面那个数组中的重复数字几乎相同，只不过是增加了一个判断相隔是否小于K位的条件，我们先用 HashMap 来做一哈，和刚才思路一致，我们直接看代码就能整懂
+
+```java
+class Solution {
+    public boolean containsNearbyDuplicate(int[] nums, int k) {
+        //特殊情况
+        if (nums.length == 0) {
+            return false;
+        }
+        // hashmap
+        HashMap<Integer,Integer> map = new HashMap<>();
+        for (int i = 0; i < nums.length; i++) {
+            // 如果含有
+            if (map.containsKey(nums[i])) {
+                //判断是否小于K，如果小于则直接返回
+                int abs = Math.abs(i - map.get(nums[i]));
+                if (abs <= k)  return true;//小于则返回        
+            }
+            //更新索引，此时有两种情况，不存在，或者存在时，将后出现的索引保存
+            map.put(nums[i],i);
+        }
+        return false;
+    }
+}
+```
+
+**HashSet**
+
+**解析**
+
+这个方法算是属于固定滑动窗口。我们需要维护一个长度为 K 的滑动窗口，如果窗口内含有该值，则直接返回 true，尾部进入新元素时，则将头部的元素去掉。继续查看是否含有该元素。下面我们来看视频解析吧，保证以下就能搞懂了。
+
+![leetcode219数组中重复元素2](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/leetcode219数组中重复元素2.6m947ehfpb40.gif)
+
+
+
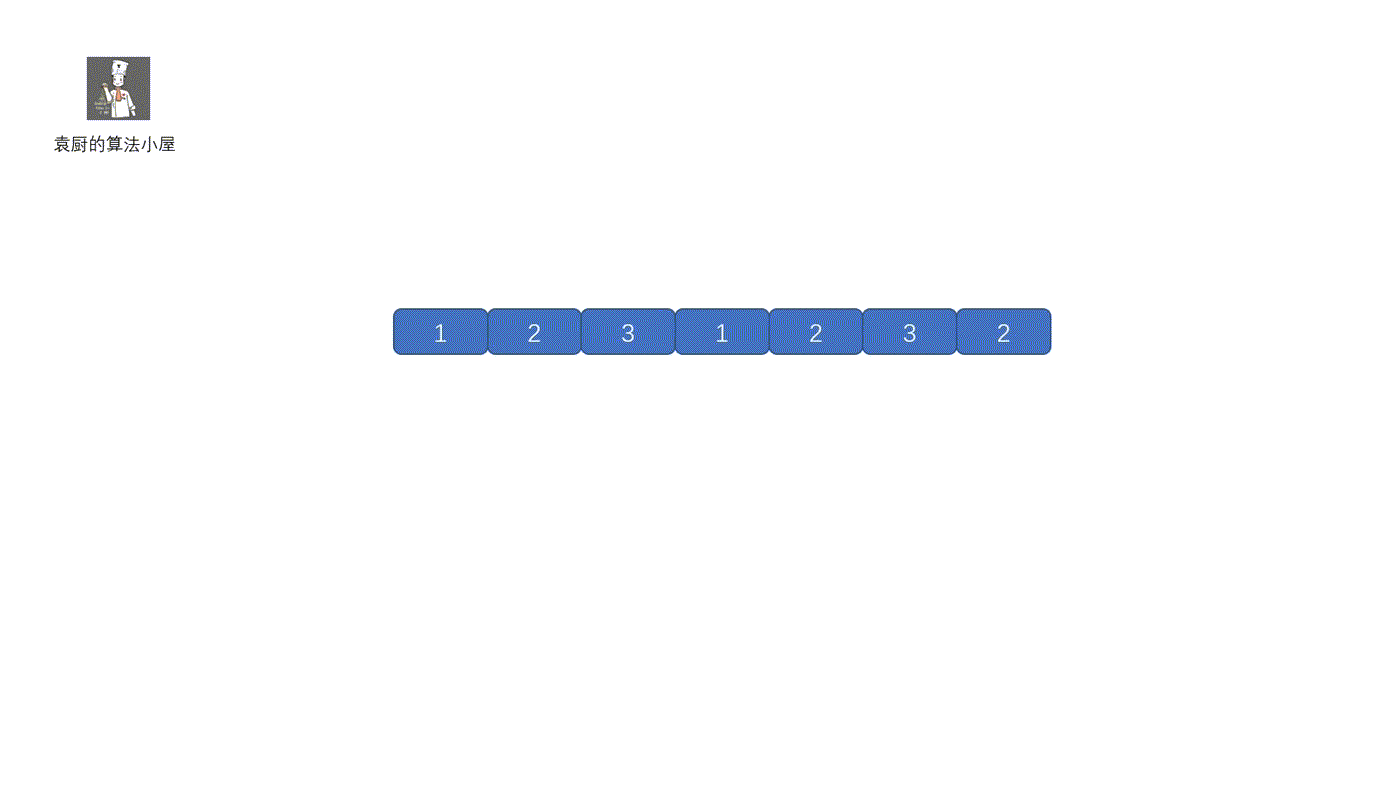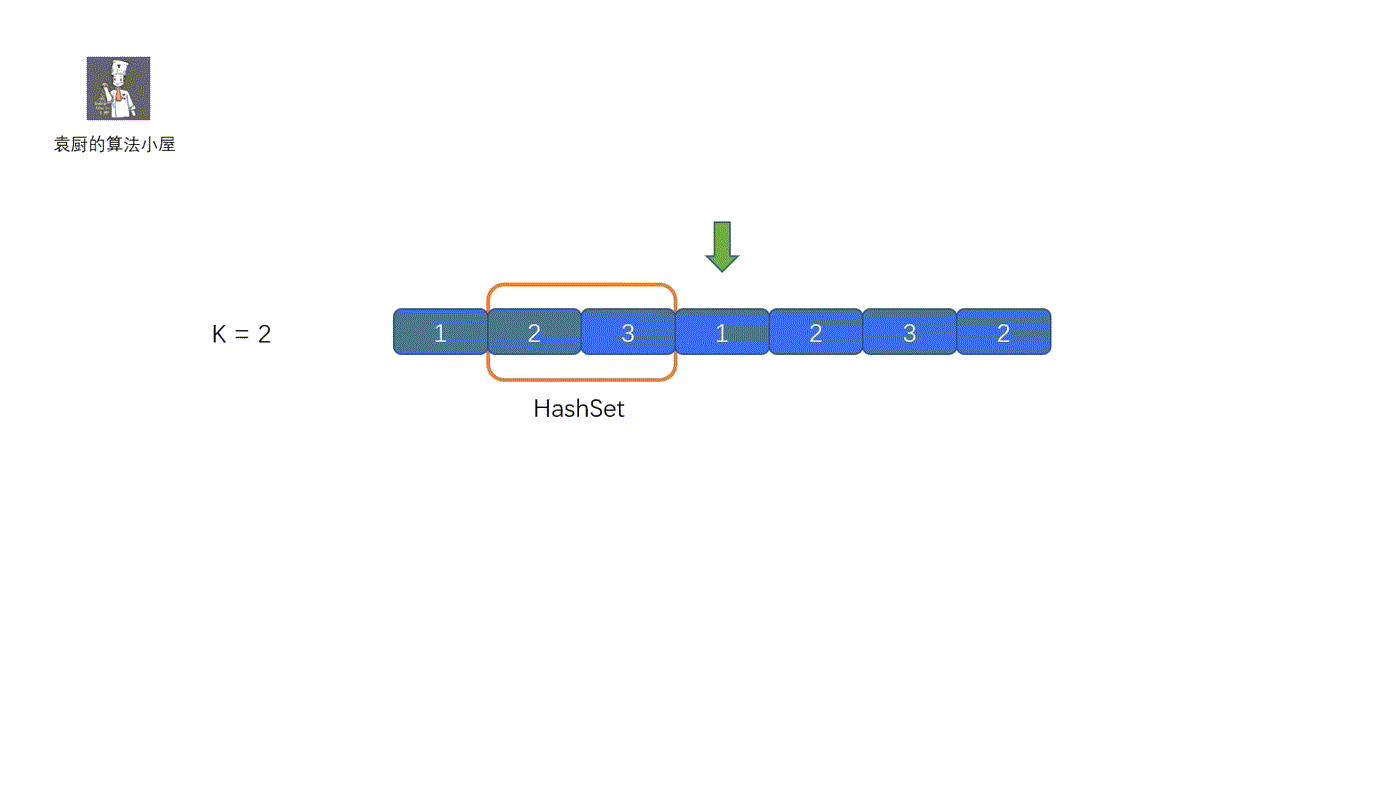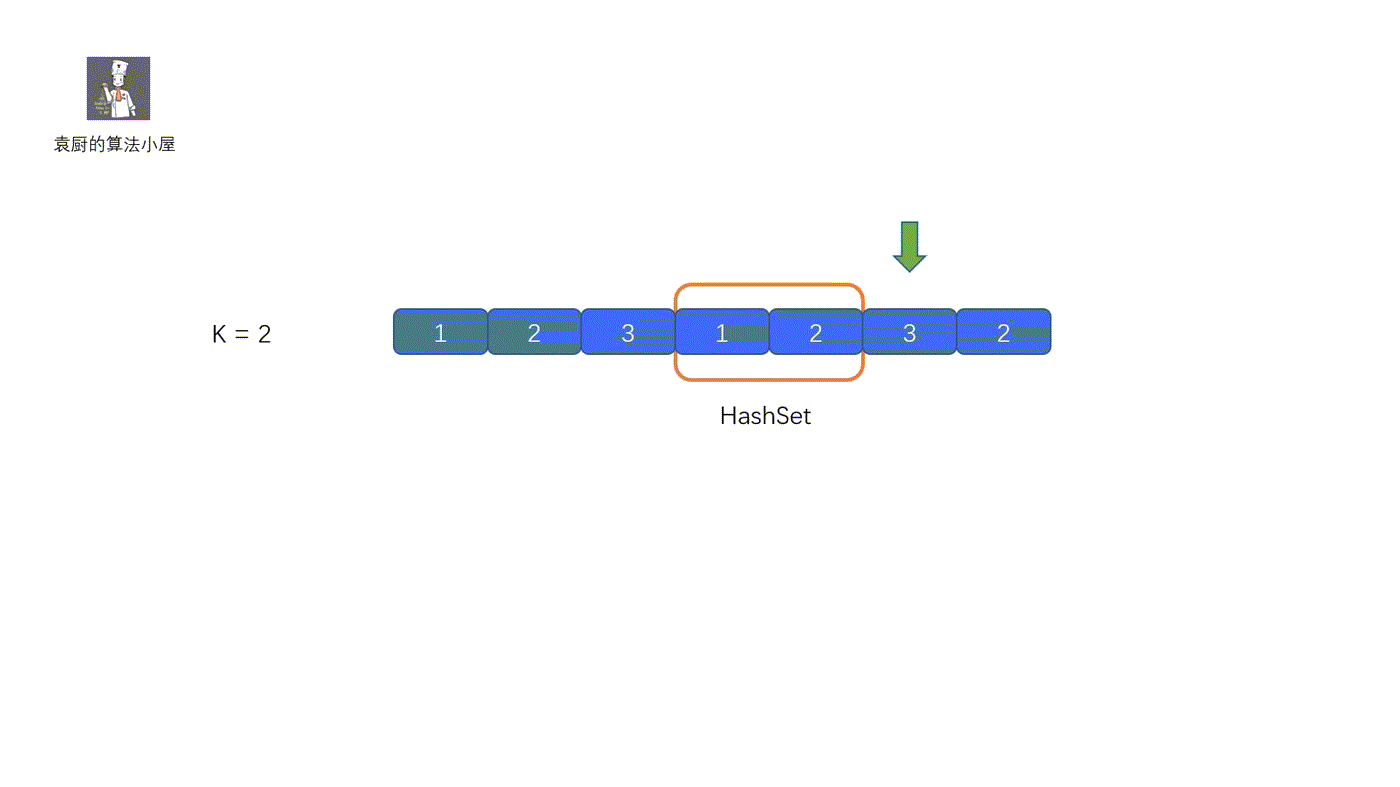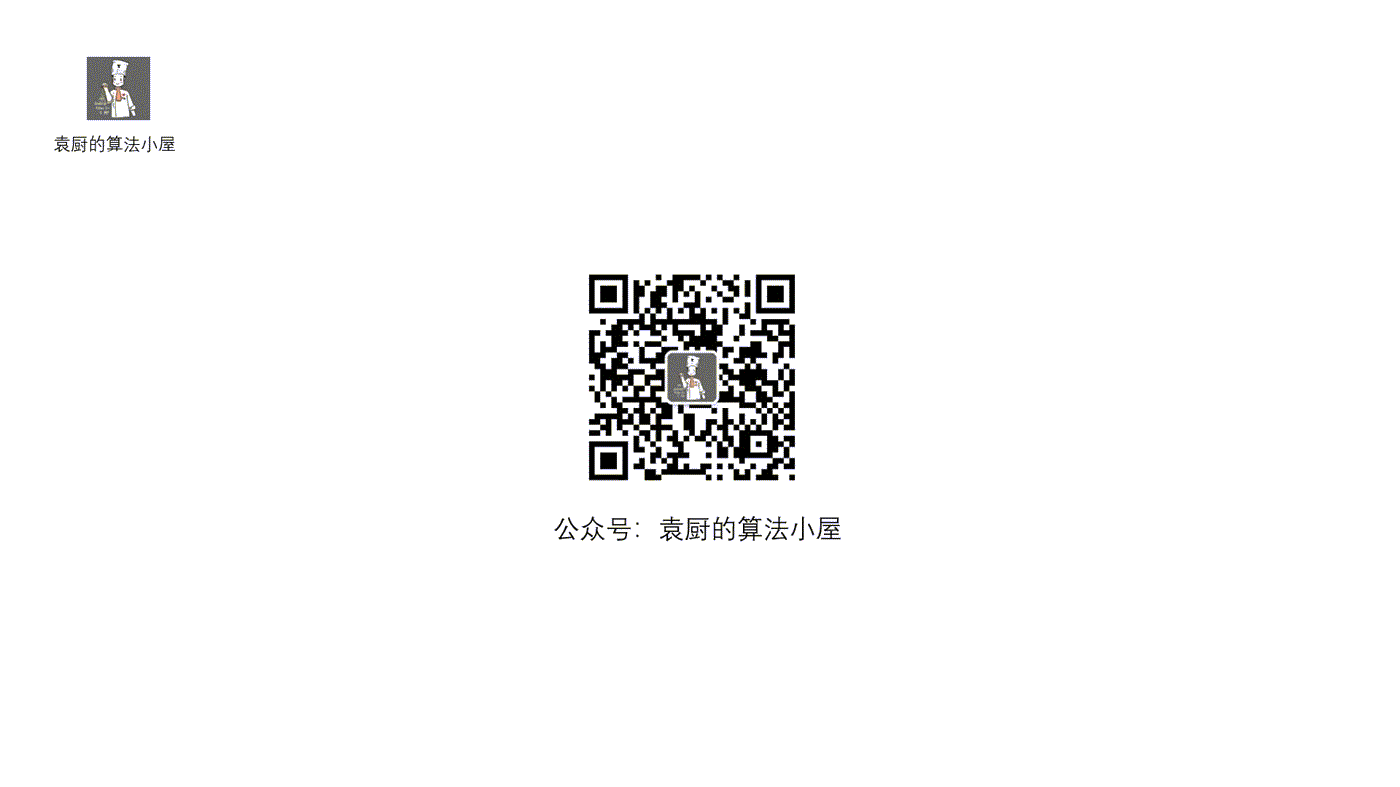
+**题目代码**
+
+```java
+class Solution {
+    public boolean containsNearbyDuplicate(int[] nums, int k) {
+        //特殊情况
+        if (nums.length == 0) {
+            return false;
+        }
+        // set
+        HashSet<Integer> set = new HashSet<>();
+        for (int i = 0; i < nums.length; ++i) {
+            //含有该元素，返回true
+            if (set.contains(nums[i])) {
+                return true;
+            }
+            // 添加新元素
+            set.add(nums[i]);
+            //维护窗口长度
+            if (set.size() > k) {
+                set.remove(nums[i-k]);
+            }
+        }
+        return false;
+    }
+}
+```
+

gif-algorithm/数组篇/leetcode485最大连续1的个数.md

@@ -0,0 +1,84 @@
+## **leetcode 485 最大连续 1 的个数**
+
+给定一个二进制数组， 计算其中最大连续1的个数。
+
+示例 1:
+
+> 输入: [1,1,0,1,1,1]
+> 输出: 3
+> 解释: 开头的两位和最后的三位都是连续1，所以最大连续1的个数是 3.
+
+我的这个方法比较奇怪，但是效率还可以，战胜了 100% , 尽量减少了 Math.max()的使用，我们来看一下具体思路，利用 right 指针进行探路，如果遇到 1 则继续走，遇到零时则停下，求当前 1 的个数。
+
+这时我们可以通过 right - left 得到 1 的 个数，因为此时我们的 right 指针指在 0 处，所以不需要和之前一样通过 right - left + 1 获得窗口长度。 
+
+然后我们再使用 while 循环，遍历完为 0 的情况，跳到下一段为 1 的情况，然后移动 left 指针。 left = right，站在同一起点，继续执行上诉过程。
+
+下面我们通过一个视频模拟代码执行步骤大家一下就能搞懂了。
+
+ ![leetcode485最长连续1的个数](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/leetcode485最长连续1的个数.7avzcthkit80.gif)
+
+
+
+
+
+下面我们直接看代码吧
+
+```java
+class Solution {
+    public int findMaxConsecutiveOnes(int[] nums) {
+
+        int len = nums.length;
+        int left = 0, right = 0;
+        int maxcount = 0;
+
+        while (right < len) {
+            if (nums[right] == 1) {
+                right++;
+                continue;
+            }
+            //保存最大值
+            maxcount = Math.max(maxcount, right - left);
+            //跳过 0 的情况
+            while (right < len && nums[right] == 0) {
+                right++;
+            }
+            //同一起点继续遍历
+            left = right;
+        }
+        return Math.max(maxcount, right-left);
+
+    }
+}
+```
+
+
+
+刚才的效率虽然相对高一些，但是代码不够优美，欢迎各位改进，下面我们说一下另外一种情况，一个特别容易理解的方法。
+
+我们通过计数器计数 连续 1 的个数，当 nums[i] == 1 时，count++，nums[i] 为 0 时，则先保存最大 count，再将 count 清零，因为我们需要的是连续的 1 的个数，所以需要清零。
+
+好啦，下面我们直接看代码吧。
+
+```java
+class Solution {
+    public int findMaxConsecutiveOnes(int[] nums) {
+
+        int count = 0;
+        int maxcount = 0;
+        
+        for (int i = 0; i < nums.length; ++i) {
+            if (nums[i] == 1) {
+                count++;
+            //这里可以改成 while
+            } else {
+                 maxcount = Math.max(maxcount,count);
+                 count = 0;
+            }
+        }
+        return Math.max(count,maxcount);
+
+    }
+}
+```
+

gif-algorithm/数组篇/leetcode560和为K的子数组.md

@@ -0,0 +1,146 @@
+### leetcode560. 和为K的子数组
+
+**题目描述**
+
+> 给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。
+
+**示例 1 :**
+
+> 输入:nums = [1,1,1], k = 2
+> 输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
+
+**暴力法**
+
+**解析**
+
+这个题目的题意很容易理解，就是让我们返回和为 k 的子数组的个数，所以我们直接利用双重循环解决该题，这个是很容易想到的。我们直接看代码吧。
+
+```java
+class Solution {
+    public int subarraySum(int[] nums, int k) {
+         int len = nums.length;
+         int sum = 0;
+         int count = 0;
+         for (int i = 0; i < len; ++i) {
+             for (int j = i; j < len; ++j) {
+                 sum += nums[j];
+                 if (sum == k) {
+                     count++;
+                 }
+             }
+             sum = 0;
+         }
+         return count;
+    }
+}
+```
+
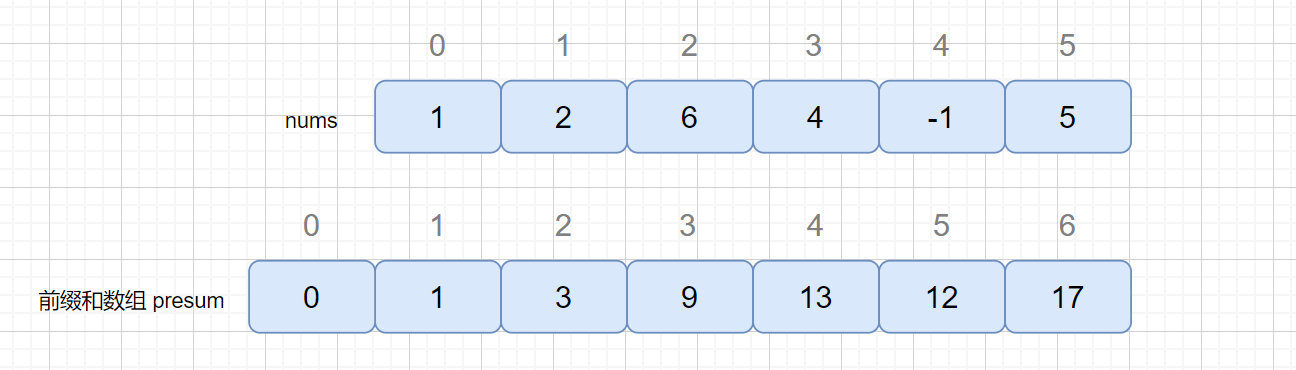
+下面我们我们使用前缀和的方法来解决这个题目，那么我们先来了解一下前缀和是什么东西。其实这个思想我们很早就接触过了。见下图
+
+![](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210113193831.4wk2b9zc8vm0.png)
+
+我们通过上图发现，我们的 presum 数组中保存的是 nums 元素的和，presum[1] = presum[0] + nums[0];
+
+presum [2] = presum[1] + nums[1],presum[3] = presum[2] + nums[2] ... 所以我们通过前缀和数组可以轻松得到每个区间的和，
+
+例如我们需要获取 nums[2] 到 nums[4] 这个区间的和，我们则完全根据 presum 数组得到，是不是有点和我们之前说的字符串匹配算法中 BM,KMP 中的 next 数组和 suffix 数组作用类似。
+
+那么我们怎么根据presum 数组获取 nums[2] 到 nums[4] 区间的和呢？见下图
+
+![前缀和](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/前缀和.77twdj3gpkg0.png)
+
+所以我们 nums[2] 到 nums[4] 区间的和则可以由 presum[5] - presum[2] 得到。
+
+也就是前 5 项的和减去前 2 项的和，得到第 3 项到第 5 项的和。那么我们可以遍历 presum 就能得到和为 K 的子数组的个数啦。
+
+直接上代码。
+
+```java
+class Solution {
+    public int subarraySum(int[] nums, int k) {
+        //前缀和数组
+        int[] presum = new int[nums.length+1];
+        for (int i = 0; i < nums.length; i++) {
+            //这里需要注意，我们的前缀和是presum[1]开始填充的
+            presum[i+1] = nums[i] + presum[i];
+        }
+        //统计个数
+        int count = 0;
+        for (int i = 0; i < nums.length; ++i) {
+            for (int j = i; j < nums.length; ++j) {
+                //注意偏移，因为我们的nums[2]到nums[4]等于presum[5]-presum[2]
+                //所以这样就可以得到nums[i,j]区间内的和
+                if (presum[j+1] - presum[i] == k) {
+                    count++;
+                }
+            }
+        }
+        return count;
+    }
+}
+```
+
+我们通过上面的例子我们简单了解了前缀和思想，那么我们如果继续将其优化呢？
+
+**前缀和 + HashMap**
+
+**解析**
+
+其实我们在之前的两数之和中已经用到了这个方法，我们一起来回顾两数之和 HashMap 的代码.
+
+```java
+class Solution {
+    public int[] twoSum(int[] nums, int target) {
+
+        HashMap<Integer,Integer> map  = new HashMap<>();
+        //一次遍历
+        for (int i = 0; i < nums.length; ++i) {
+            //存在时，我们用数组得值为 key，索引为 value
+            if (map.containsKey(target - nums[i])){              
+               return new int[]{i,map.get(target-nums[i])};
+            }
+            //存入值
+            map.put(nums[i],i);
+        }
+        //返回
+        return new int[]{};
+    }
+}
+```
+
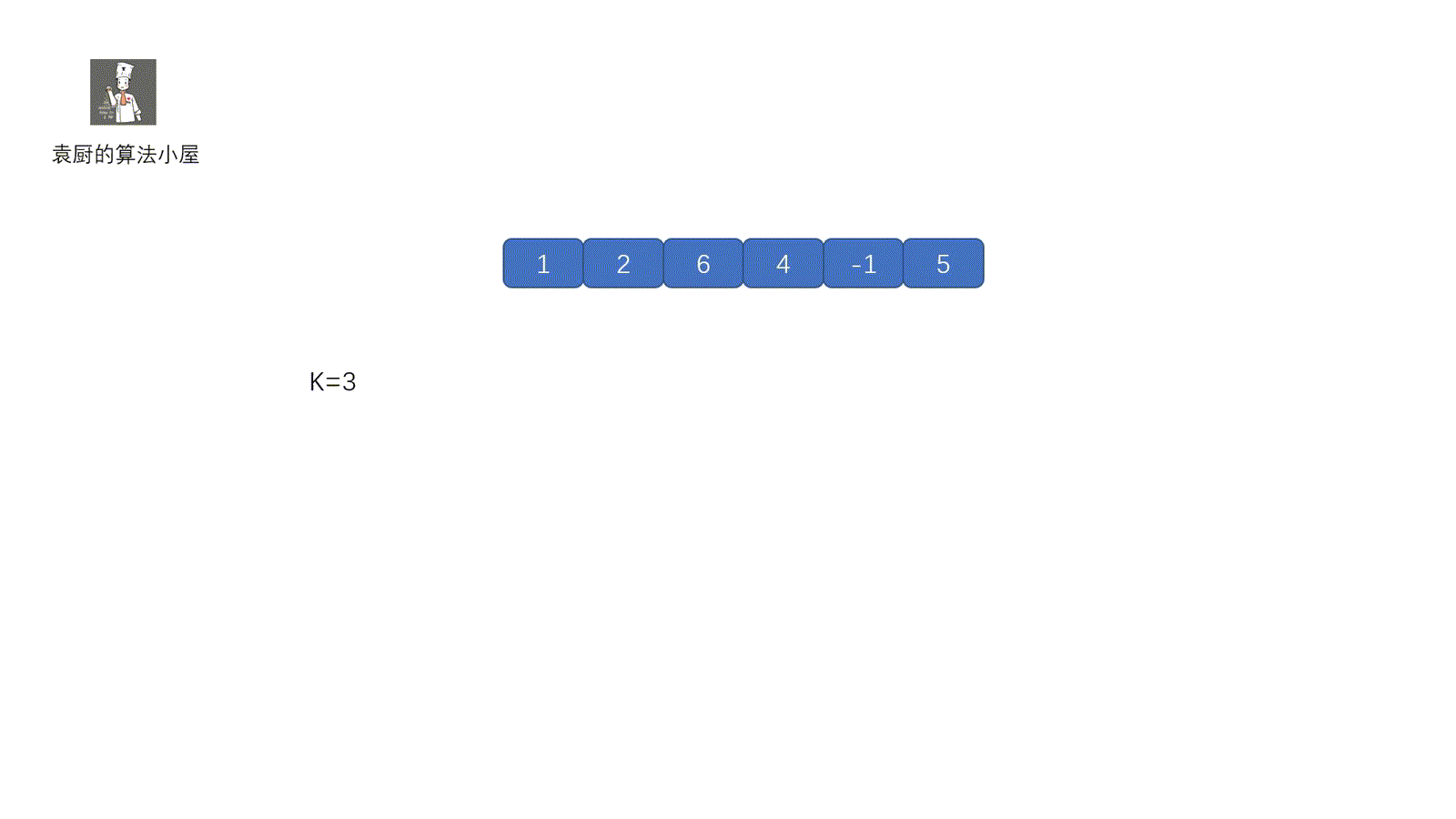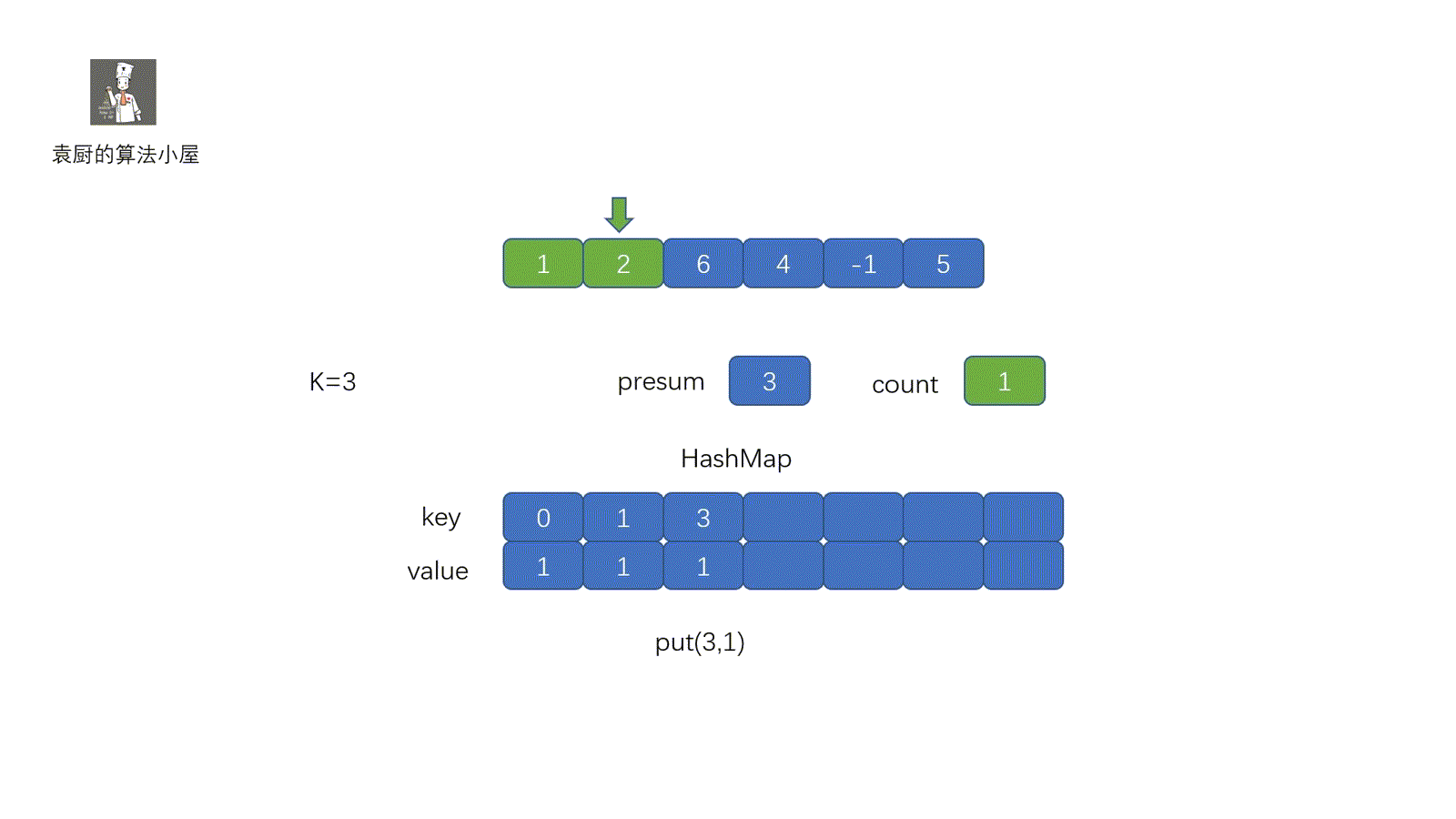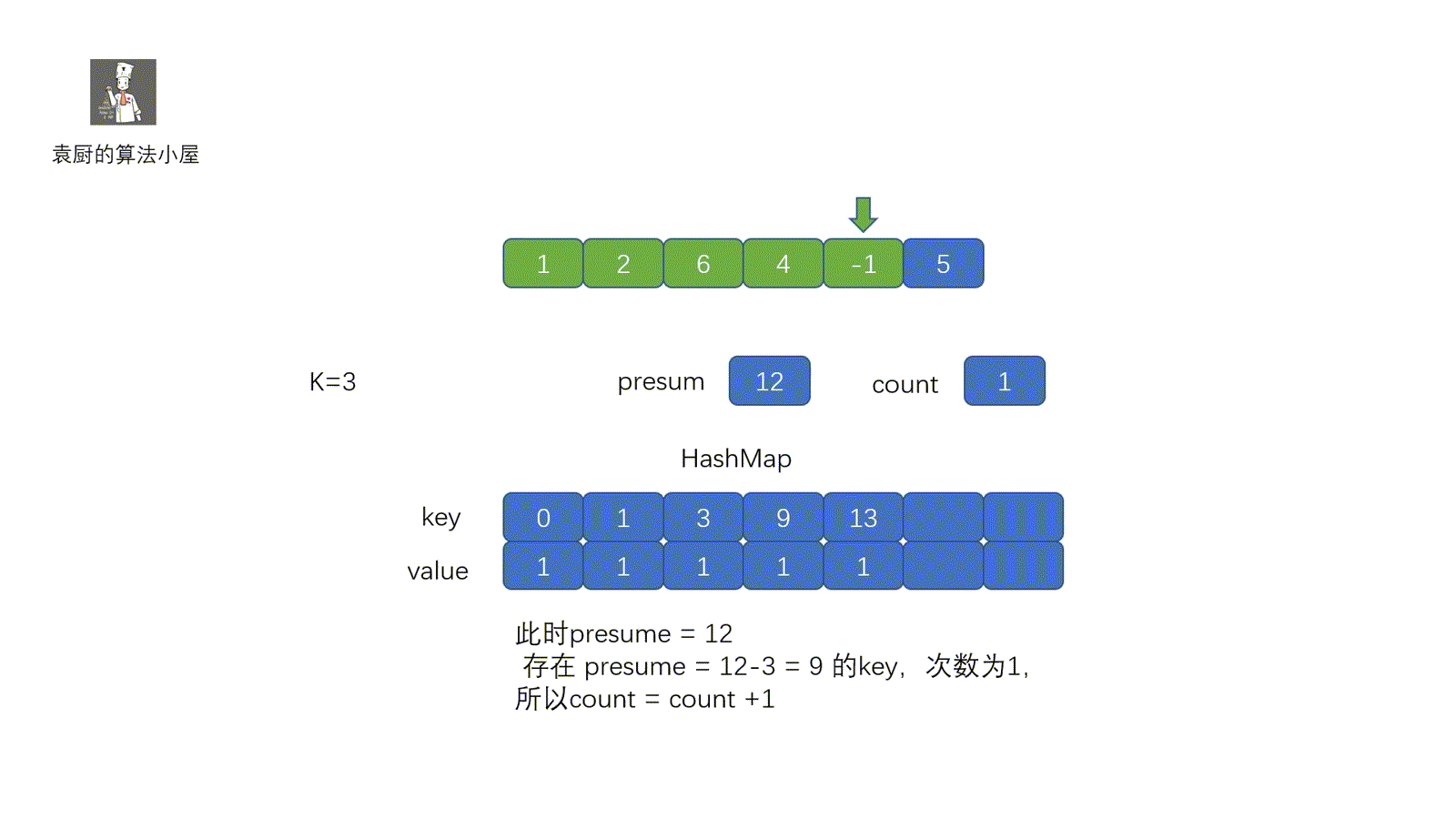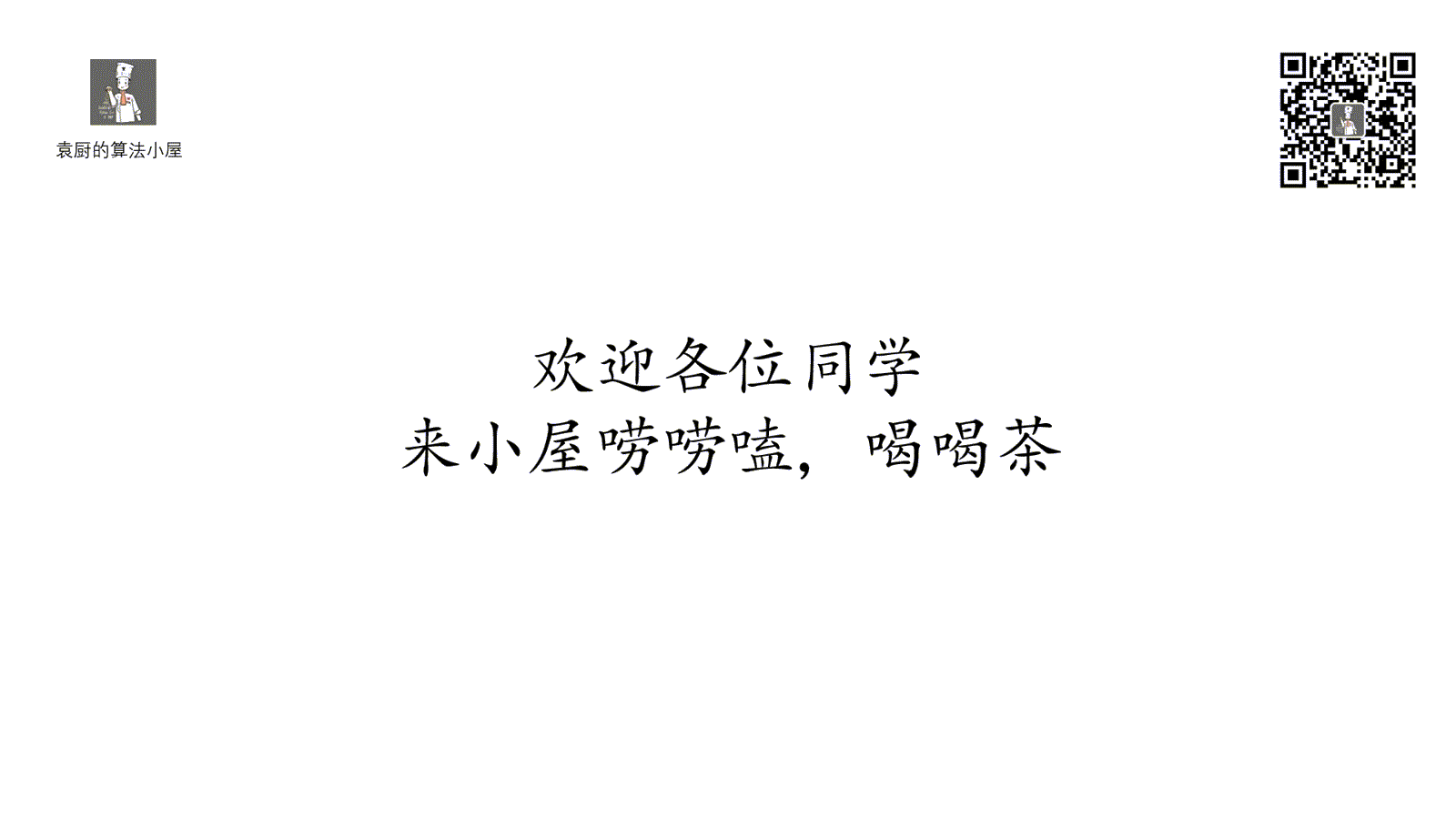
+上面代码中，我们将数组的值和索引存入 map 中，当我们遍历到某一值 x 时，判断 map 中是否含有 target - x，即可。其实我们现在这个题目和两数之和原理是一致的，只不过我们是将**所有的前缀和**该**前缀和出现的次数**存到了 map 里。下面我们来看一下代码的执行过程。
+
+**动图解析**
+
+![leetcode560和为k的子数组](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/leetcode560和为k的子数组.1266gnukwxr4.gif)
+
+**题目代码**
+
+```java
+class Solution {
+    public int subarraySum(int[] nums, int k) {
+        if (nums.length == 0) {
+            return 0;
+        }
+        HashMap<Integer,Integer> map = new HashMap<>();
+        //细节，这里需要预存前缀和为 0 的情况，会漏掉前几位就满足的情况
+        //例如输入[1,1,0]，k = 2 如果没有这行代码，则会返回0,漏掉了1+1=2，和1+1+0=2的情况
+        //输入：[3,1,1,0] k = 2时则不会漏掉
+        //因为presum[3] - presum[0]表示前面 3 位的和，所以需要map.put(0,1),垫下底
+        map.put(0, 1);
+        int count = 0;
+        int presum = 0;
+        for (int x : nums) {
+            presum += x;
+            //当前前缀和已知，判断是否含有 presum - k的前缀和，那么我们就知道某一区间的和为 k 了。
+            if (map.containsKey(presum - k)) {
+                count += map.get(presum - k);//获取presum-k前缀和出现次数
+            }
+            //更新
+            map.put(presum,map.getOrDefault(presum,0) + 1);
+        }
+        return count;
+    }
+}
+```
+

gif-algorithm/数组篇/leetcode66加一.md

@@ -0,0 +1,60 @@
+### leetcode 66 加一
+
+**题目描述**
+
+> 给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。
+>
+> 最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。
+>
+> 你可以假设除了整数 0 之外，这个整数不会以零开头。
+
+**示例 1：**
+
+> 输入：digits = [1,2,3]
+> 输出：[1,2,4]
+> 解释：输入数组表示数字 123。
+
+**示例 2：**
+
+> 输入：digits = [4,3,2,1]
+> 输出：[4,3,2,2]
+> 解释：输入数组表示数字 4321。
+
+**示例 3：**
+
+输入：digits = [0]
+输出：[1]
+
+**数组遍历**
+
+**题目解析**
+
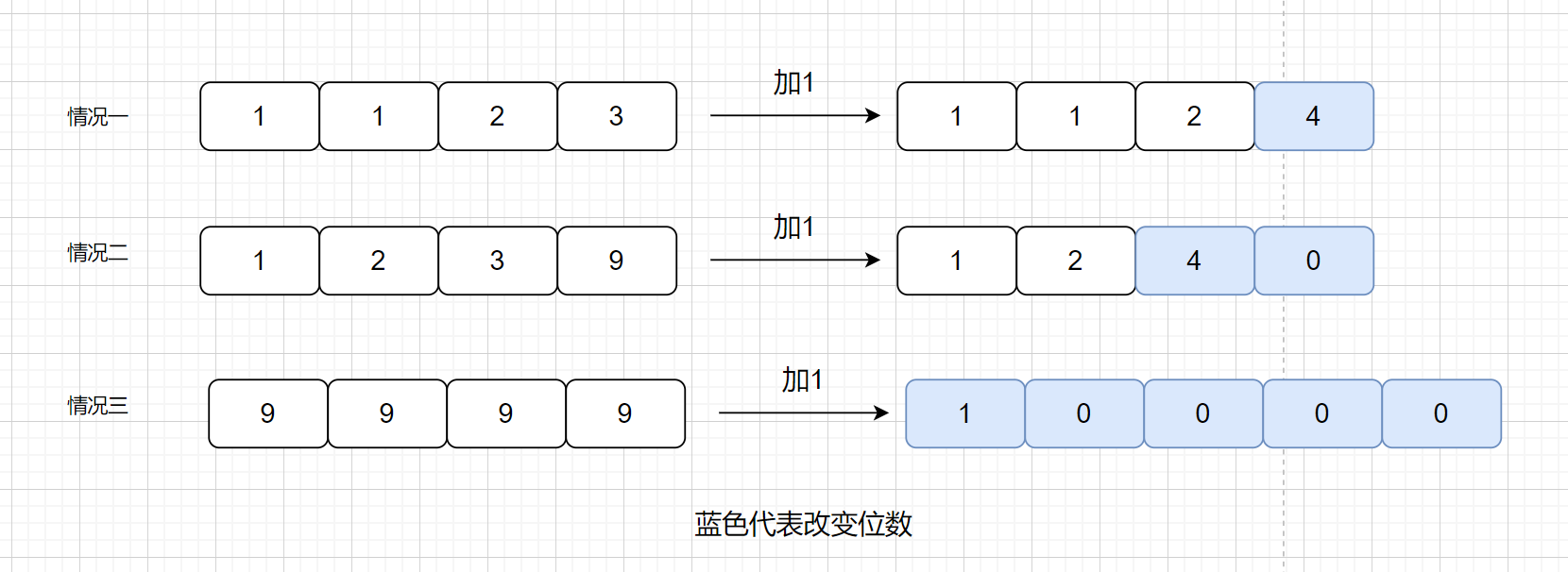
+我们思考一下，加一的情况一共有几种情况呢？是不是有以下三种情况
+
+![加一](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/加一.3lp9zidw61s0.png)
+
+则我们根据什么来判断属于第几种情况呢？
+
+我们可以根据当前位 余10来判断，这样我们就可以区分属于第几种情况了，大家直接看代码吧，很容易理解的。
+
+```java
+class Solution {
+    public int[] plusOne(int[] digits) {
+        //获取长度
+        int len = digits.length;
+        for (int i = len-1; i >= 0; i--) {
+            digits[i] = (digits[i] + 1) % 10;
+            //第一种和第二种情况，如果此时某一位不为 0 ，则直接返回即可。
+            if (digits[i] != 0) {
+                return digits;
+            }
+        
+        }
+        //第三种情况，因为数组初始化每一位都为0，我们只需将首位设为1即可
+        int[] arr = new int[len+1]; 
+        arr[0] = 1;
+        return arr;
+    }
+}
+```
+

gif-algorithm/数组篇/leetcode75颜色分类.md

@@ -0,0 +1,111 @@
+### leetcode 75 颜色分类
+
+**题目描述**
+
+> 给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
+>
+> 此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
+
+**示例 1：**
+
+> 输入：nums = [2,0,2,1,1,0]
+> 输出：[0,0,1,1,2,2]
+
+**示例 2：**
+
+> 输入：nums = [2,0,1]
+> 输出：[0,1,2]
+
+示例 3：
+
+> 输入：nums = [0]
+> 输出：[0]
+
+示例 4：
+
+> 输入：nums = [1]
+> 输出：[1]
+
+**两次遍历**
+
+**解析：**
+
+通过两次遍历，第一遍遍历首先将 0 归位，第二遍遍历将 1 归位，自然 2 也就被归位了，这个方法很容易理解我们直接看代码吧。
+
+**题目代码**
+
+```java
+class Solution {
+    public void sortColors(int[] nums) {
+        int pro = 0;
+        //将0归位
+        for (int i = 0; i < nums.length; ++i) {
+            if (nums[i] == 0) {
+                swap(nums,i,pro);
+                pro++;
+            }        
+        }
+        //将1归位
+        for (int j = pro; j < nums.length; ++j) {
+            if(nums[j] == 1) {
+                swap(nums,j,pro);
+                pro++;
+            }
+        }
+    }
+    public void swap(int[] nums,int i, int j) {
+        int temp = nums[i];
+        nums[i] = nums[j];
+        nums[j] = temp;
+    }
+}
+```
+
+  **一次遍历**
+
+**解析**
+
+两次遍历实现是十分容易的，也很容易实现，那么我们可不可以一次遍历就将其归位呢？其实这里也利用了我们双指针的思想，我们首先定义两个指针，一个位于数组头部，一个位于数组尾部，当我们遇到 0 时则给我们头部指针交换，遇到 2 时，则给尾部指针交换。不过里面有两个细节我们需要注意。
+
+1.遍历数组时，指针的上界，不能是 i < nums.length;应是 i <= right;
+
+2.需要注意交换后，当前指针指向的仍不为1。
+
+干看上面两种注意事项，可能不是特别容易理解，我们来看我们的视频解析，就可以搞懂这两个情况啦。
+
+**动图解析**
+
+![leetcode75颜色分类](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/leetcode75颜色分类.5w4sa458rr40.gif)
+
+**题目代码**
+
+```java
+class Solution {
+    public void sortColors(int[] nums) {
+        int len = nums.length;
+        int left = 0;
+        int right = len-1;
+        //注意看 for 循环的结束条件
+        for (int i = 0; i <= right; ++i) {
+            if (nums[i] == 0) {
+                swap(nums,i,left);
+                left++;
+            }
+            if (nums[i] == 2) {
+                swap(nums,i,right);
+                right--;
+                // 发现此时不为1，则指针不移动，继续交换
+                if (nums[i] != 1) {
+                    i--;
+                }
+            }
+        }
+    }
+    public void swap (int[] nums, int i, int j) {
+        int temp = nums[i];
+        nums[i] = nums[j];
+        nums[j] = temp;
+    }
+}
+```
+

gif-algorithm/数组篇/剑指offer3数组中重复的数.md

@@ -0,0 +1,76 @@
+### 剑指 offer 3 数组中重复的数字
+
+**题目描述**
+
+找出数组中重复的数字。
+
+
+在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
+
+示例 1：
+
+输入：
+[2, 3, 1, 0, 2, 5, 3]
+输出：2 或 3 
+
+**HashSet**
+
+**解析**
+
+这种题目或许一下就让人想到 HashSet，题目描述很清楚就是让我们找到数组中重复的元素，那我们第一下想到的就是 HashSet，我们遍历数组，如果发现 set 含有该元素则返回，不含有则存入哈希表，题目代码也很简单
+
+**题目代码**
+
+```java
+class Solution {
+    public int findRepeatNumber(int[] nums) {
+        // HashSet
+        HashSet<Integer> set = new HashSet<Integer>();
+        for (int x : nums) {
+            //发现某元素存在，返回
+            if (set.contains(x)) {
+                return x;
+            }
+            //存入哈希表
+            set.add(x);
+        }
+        return -1;
+    }
+}
+```
+
+**原地置换**
+
+**解析**
+
+这一种方法也是我们经常用到的，主要用于重复出现的数，缺失的数等题目中，下面我们看一下这个原地置换法，原地置换的大体思路就是将我们**指针对应**的元素放到属于他的位置（索引对应的地方）。我们可以这样理解，每个人都有自己的位置，我们需要和别人调换回到属于自己的位置，调换之后，如果发现我们的位置上有人了，则返回。大致意思了解了，下面看代码的执行过程。通过视频一下就可以搞懂啦。
+
+![剑指offer3数组中重复的数](https://cdn.jsdelivr.net/gh/tan45du/test1@master/20210122/剑指offer3数组中重复的数.2p6cd5os0em0.gif)
+
+
+
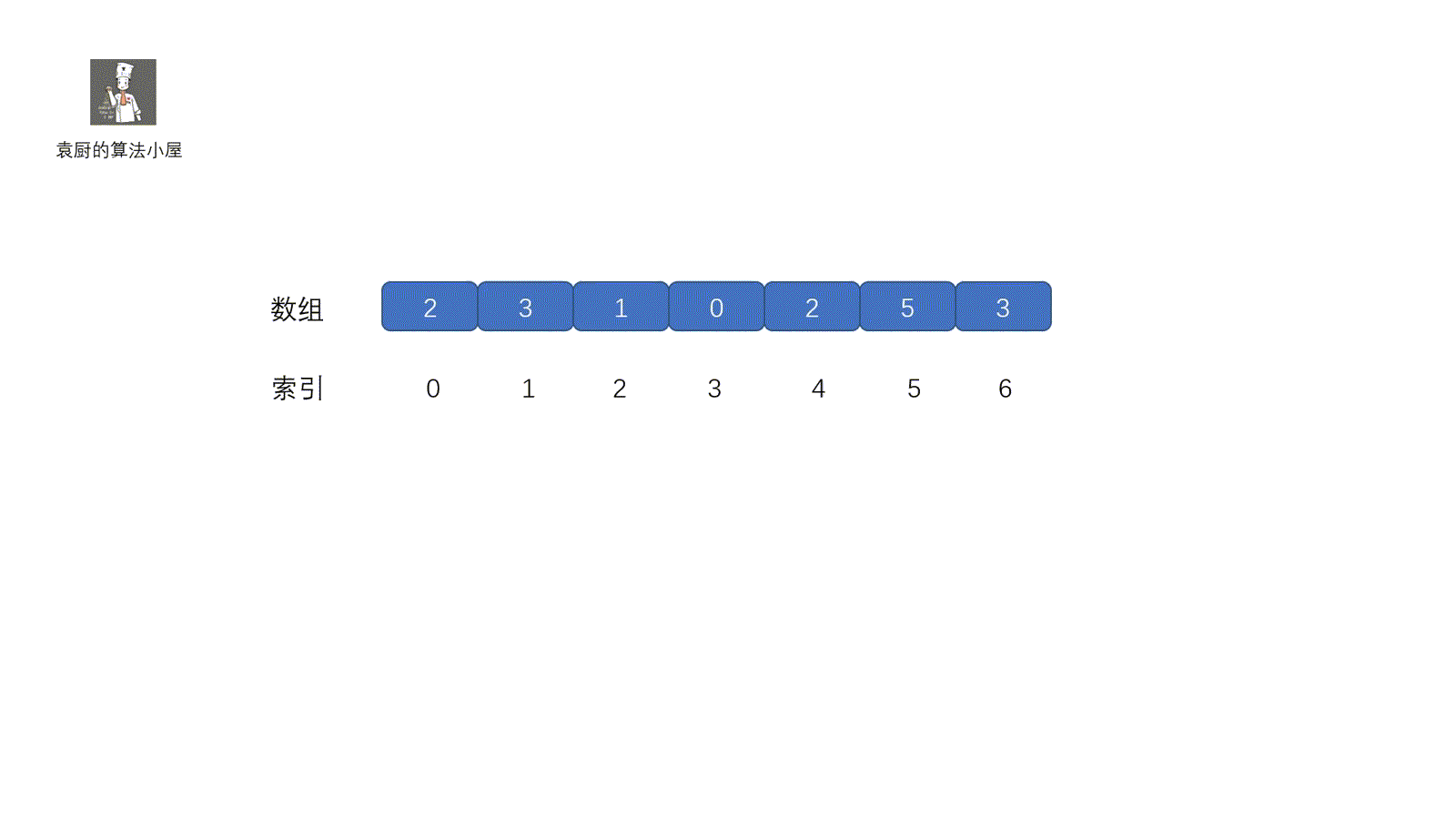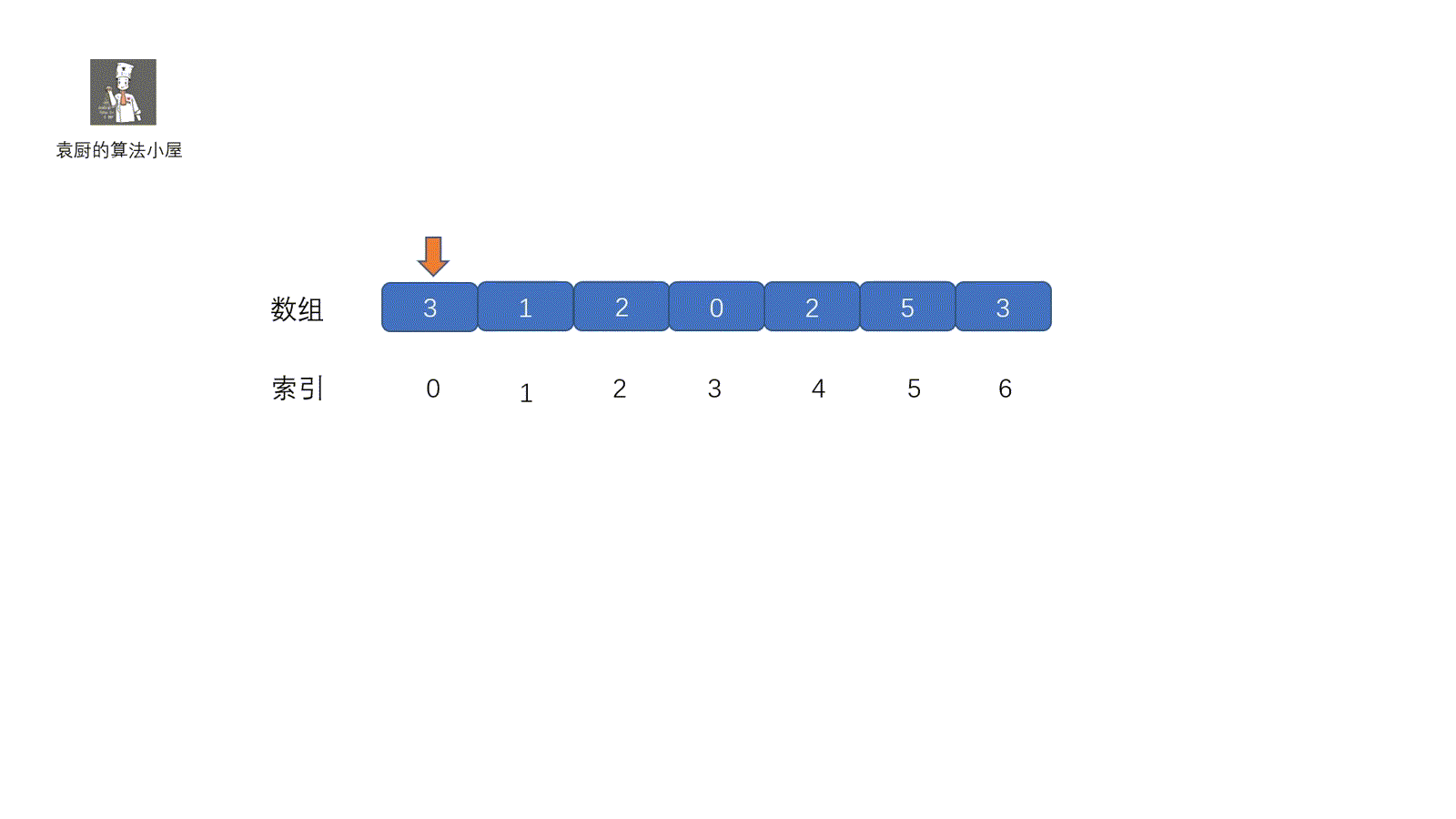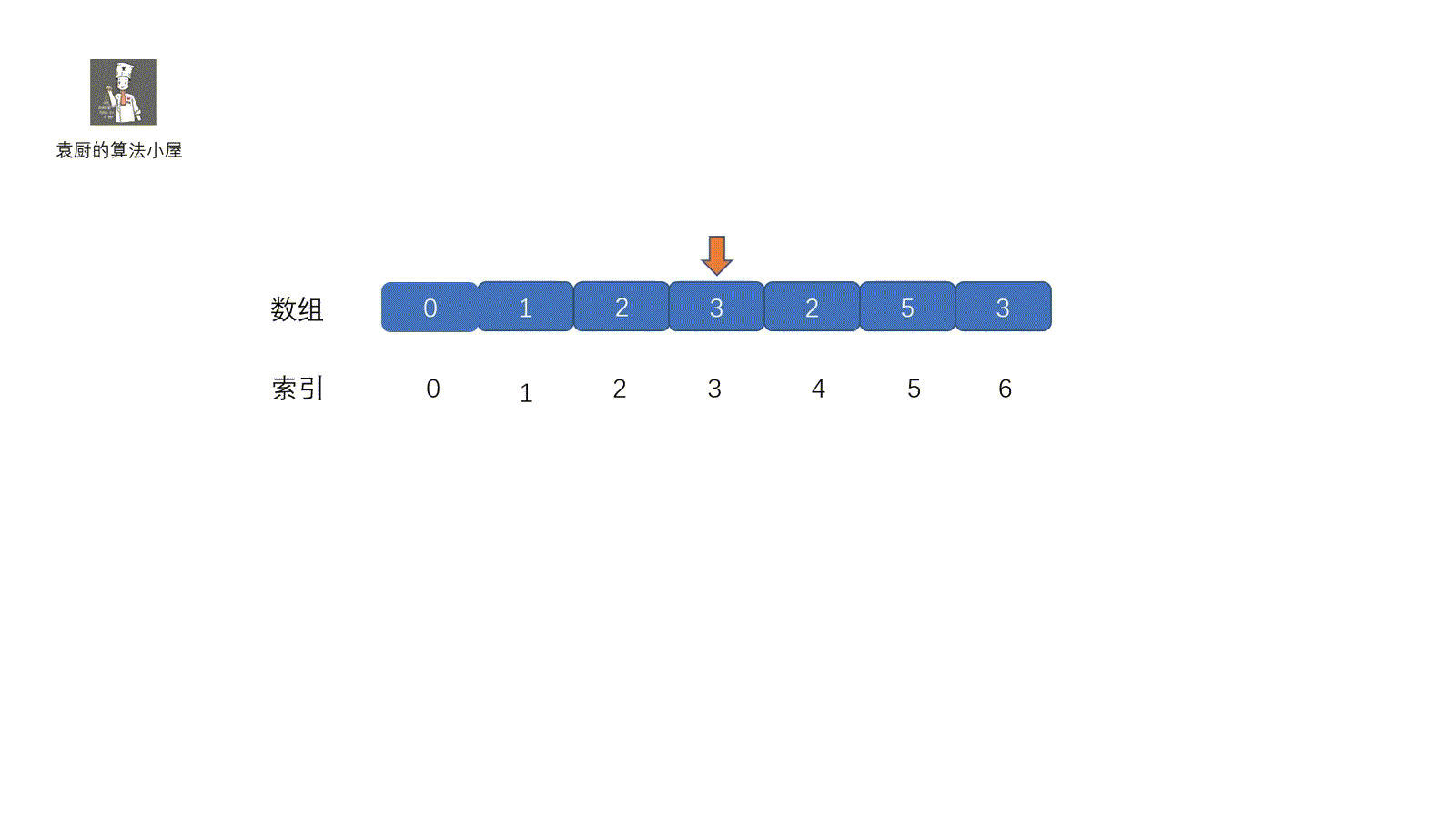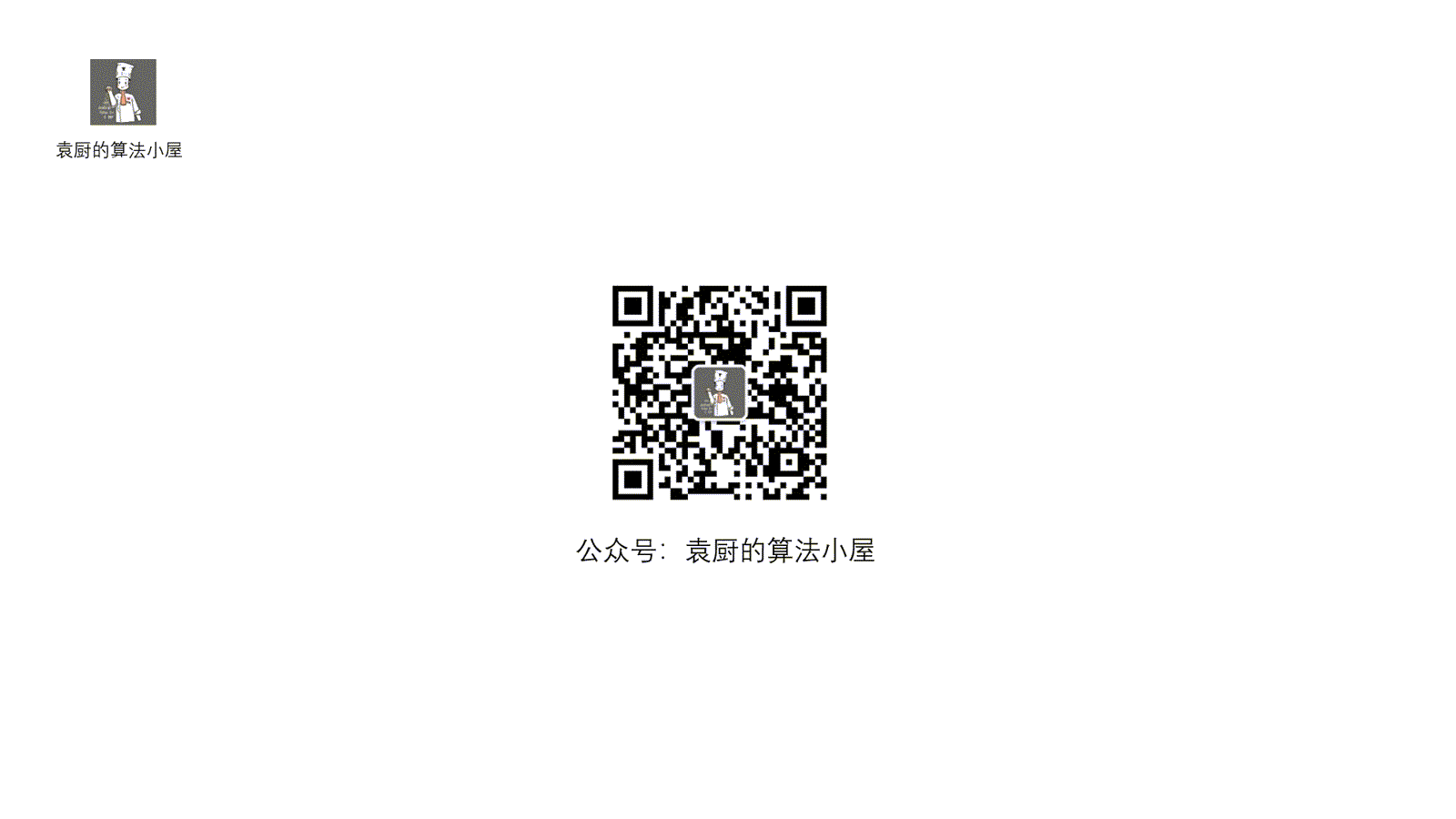
+**题目代码**
+
+```java
+class Solution {
+    public int findRepeatNumber(int[] nums) {
+        if (nums.length == 0) {
+            return -1;
+        }
+        for (int i = 0; i < nums.length; ++i) {
+            while (nums[i] != i) {
+                //发现重复元素
+                if (nums[i] == nums[nums[i]]) {
+                    return nums[i];
+                }
+                //置换，将指针下的元素换到属于他的索引处
+                int temp = nums[i];
+                nums[i] = nums[temp];
+                nums[temp] = temp;
+            }
+        }
+        return -1;
+    }
+}
+```
+