mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2026-03-10 20:04:44 +00:00
2021.3.19
This commit is contained in:
156
gif-algorithm/数据结构和算法/关于栈和队列的那些事.md
Normal file
156
gif-algorithm/数据结构和算法/关于栈和队列的那些事.md
Normal file
@@ -0,0 +1,156 @@
|
||||
# 希望这篇文章能合你的胃口
|
||||
|
||||
大家在学习数据结构的时候应该都学习过栈和队列,对他俩的原理应该很熟悉了,栈是先进后出,队列是后进后出。下面我们通过这篇文章来帮助小伙伴们回忆一下栈和队列的那些事。
|
||||
|
||||
阅读完这篇文章你会有以下收获。
|
||||
|
||||
了解栈和队列的意义
|
||||
|
||||
了解栈和队列的实现方式
|
||||
|
||||
了解循环队列
|
||||
|
||||
学会中缀表达式转后缀表达式
|
||||
|
||||
学会后缀表达式的运算
|
||||
|
||||
## 这是栈
|
||||
|
||||
### 栈模型
|
||||
|
||||
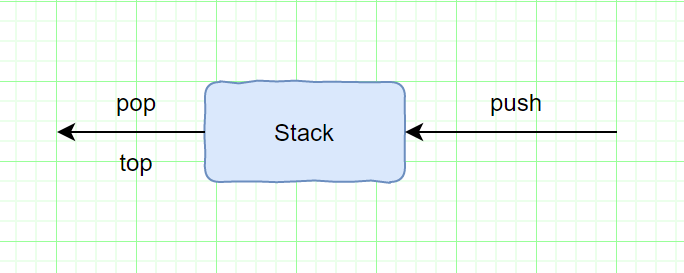
**栈(stack)是限制插入和删除只能在一个位置上进行的表**,该位置是表的末端叫做栈的顶(top),对栈的基本操作有push(进栈)和pop(出栈),前者相当于插入,后者则是删除最后插入的元素。
|
||||
|
||||
栈的另一个名字是LIFO(先进后出)表。普通的清空栈的操作和判断是否空栈的测试都是栈的操作指令系统的一部分,我们对栈能做的基本上也就是push和pop操作。
|
||||
|
||||
注:该图描述的模型只象征着push是输入操作,pop和top是输出操作
|
||||
|
||||
|
||||
|
||||
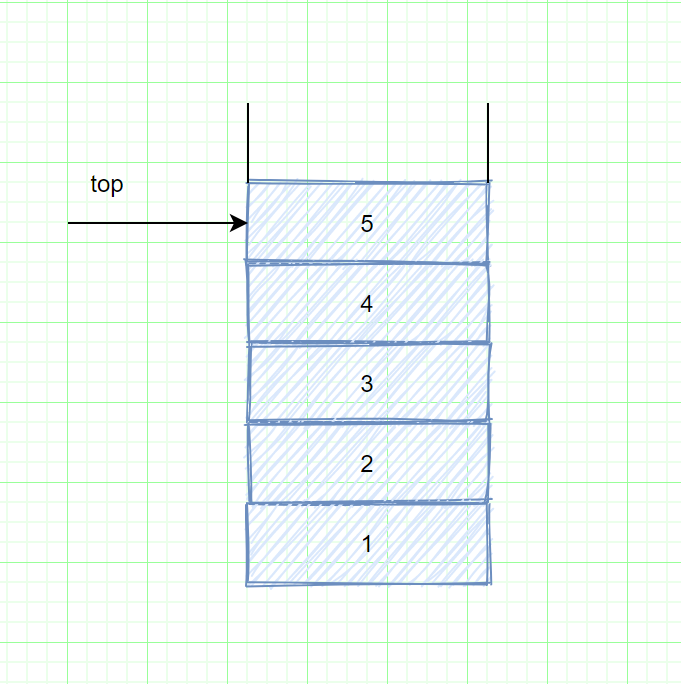
下图表示进行若干操作后的一个抽象的栈。一般的模型是,存在某个元素位于栈顶,而该元素是唯一可见元素。
|
||||
|
||||
|
||||
|
||||
### 栈的实现
|
||||
|
||||
因为栈是一个表,因此能够实现表的方法都可以实现栈,ArrayList和LinkedList都可以支持栈操作。
|
||||
|
||||
刷题时我们可以直接使用Stack类来进行创建一个栈。刷题时我们可以通过下列代码创建一个栈。下面两种方式哪种都可以使用。
|
||||
|
||||
```
|
||||
Deque<TreeNode> stack = new LinkedList<TreeNode>();//类型为TreeNode
|
||||
Stack<TreeNode> stack = new Stack<TreeNode>();
|
||||
```
|
||||
|
||||
### 栈的应用
|
||||
|
||||
栈在现实中应用场景很多,大家在刷题时就可以注意到,很多题目都可以用栈来解决的。下面我们来说一个比较常用的情景,数字表达式的求值。
|
||||
|
||||
不知道大家是否还记得那句口令,先乘除,后加减,从左算到右,有括号的话就先算括号里面的。这是我们做小学数学所用到的。四则运算中括号也是其中的一部分,先乘除后加减使运算变的复杂,加上括号后甚之,那么我们有什么办法可以让其变的更好处理呢?波兰数学家**Jan Łukasiewicz**想到了一种不需要括号的后缀表达式,,我们也将它称之为逆波兰表示。不用数学家名字命名的原因有些尴尬,居然是因为他的名字太复杂了,所以用了国籍来表示而不是姓名。所以各位小伙伴以后给孩子起名字的时候不要太复杂啊。
|
||||
|
||||
> 扬·武卡谢维奇([波兰语](https://baike.baidu.com/item/波兰语):*Jan Łukasiewicz*,1878年12月21日[乌克兰](https://baike.baidu.com/item/乌克兰)利沃夫 - 1956年2月13日爱尔兰都柏林),[波兰](https://baike.baidu.com/item/波兰)数学家,主要致力于[数理逻辑](https://baike.baidu.com/item/数理逻辑)的研究。著名的波兰表示法逆波兰表示法就是他的研究成果。
|
||||
|
||||
#### 中缀表达式转为后缀表达式
|
||||
|
||||
我们通过一个例子,来说明如何将中缀表达式转为后缀表达式。
|
||||
|
||||
例
|
||||
|
||||
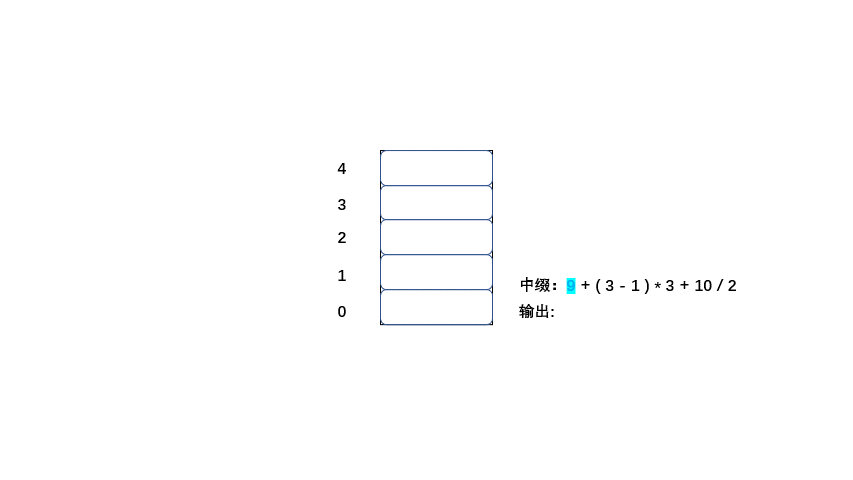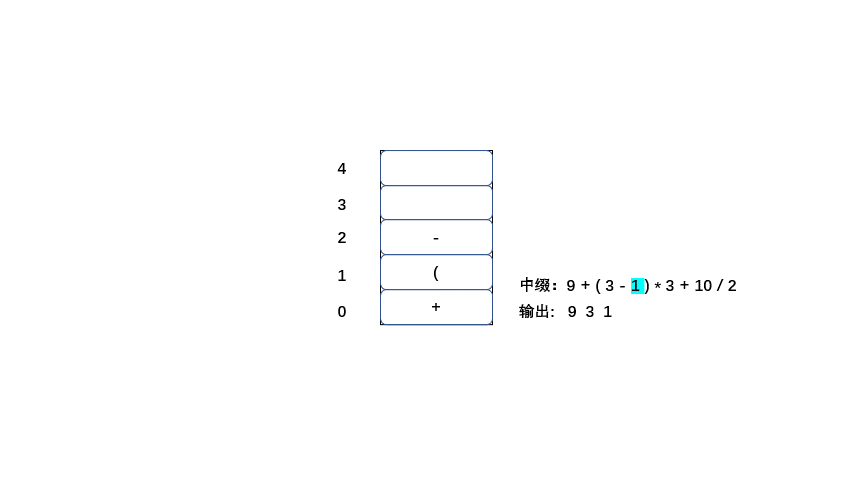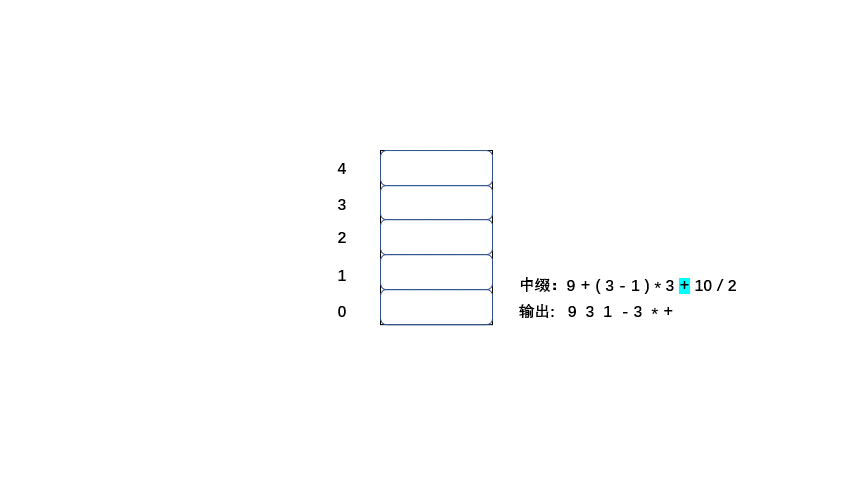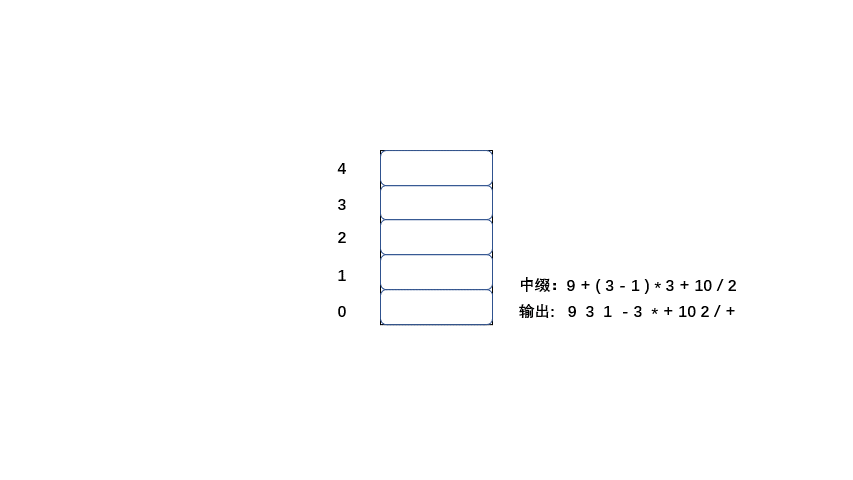
中缀:9 + ( 3 - 1 ) * 3 + 10 / 2
|
||||
|
||||
后缀:9 3 1 - 3 * + 10 2 / +
|
||||
|
||||
规则
|
||||
|
||||
1.从左到右遍历中缀表达式的每个数字和符号,若是数字就输出(直接成为后缀表达式的一部分,不进入栈)
|
||||
|
||||
2.若是符合则判断其与栈顶符号的优先级,是右括号或低于栈顶元素,则栈顶元素依次出栈并输出,等出栈完毕,当前元素入栈。
|
||||
|
||||
3.遵循以上两条直到输出后缀表达式为止。
|
||||
|
||||
老样子大家直接看动图吧简单粗暴,清晰易懂
|
||||
|
||||
|
||||
|
||||
#### 后缀表达式计算结果
|
||||
|
||||
中缀:9 + ( 3 - 1 ) * 3 + 10 / 2=20
|
||||
|
||||
后缀:9 3 1 - 3 * + 10 2 / +
|
||||
|
||||
后缀表达式的值也为20,那么我们来了解一下计算机是如何将后缀表达式计算为20的。
|
||||
|
||||
规则:
|
||||
|
||||
1.从左到右遍历表达式的每个数字和符号,如果是数字就进栈
|
||||
|
||||
2.如果是符号就将栈顶的两个数字出栈,进行运算,并将结果入栈,一直到获得最终结果。
|
||||
|
||||
下面大家 继续看动图吧。
|
||||
|
||||
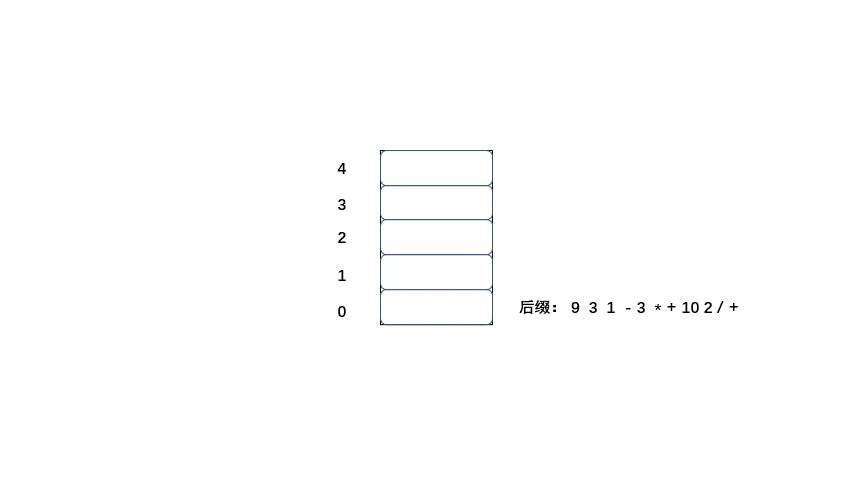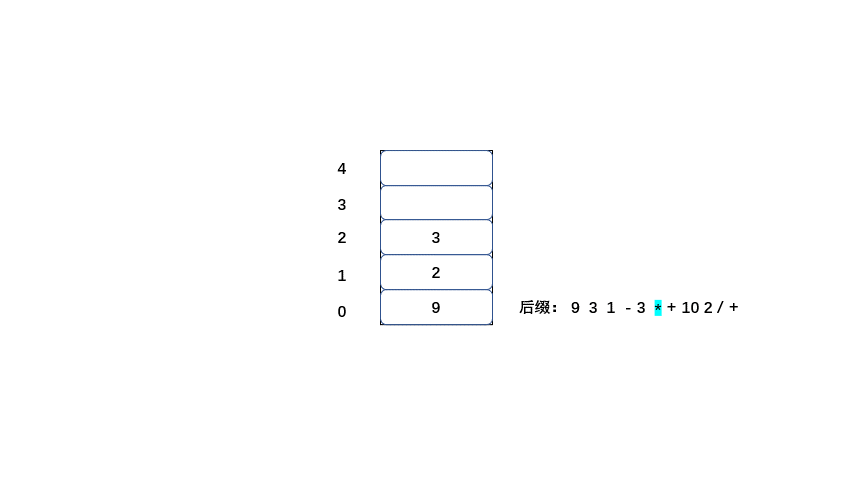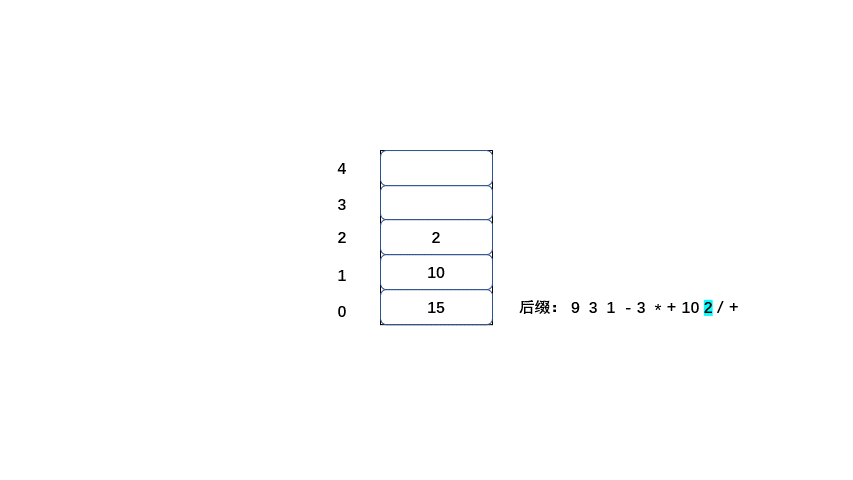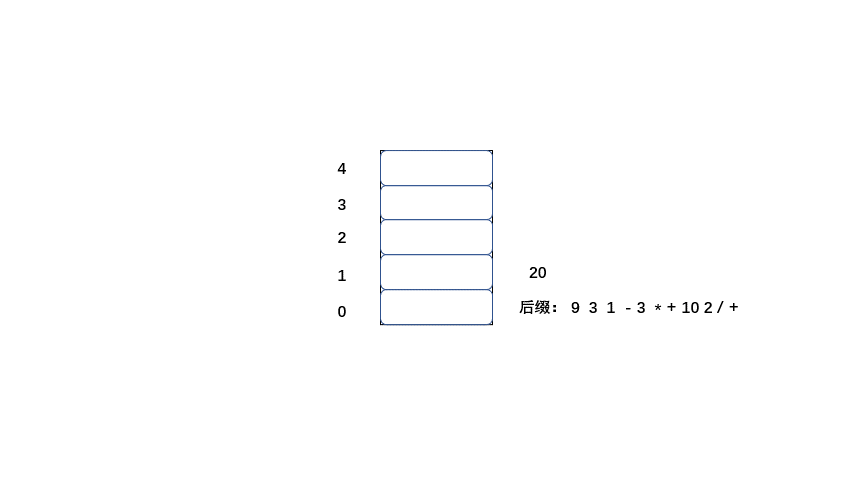
|
||||
|
||||
|
||||
|
||||
注:为了用动图把逻辑整的清晰明了,十几秒的动图,就要整半个多小时,改进好几遍。如果觉得图片对你有帮助的话就点个赞和在看吧。
|
||||
|
||||
## 这是队列
|
||||
|
||||
### 队列模型
|
||||
|
||||
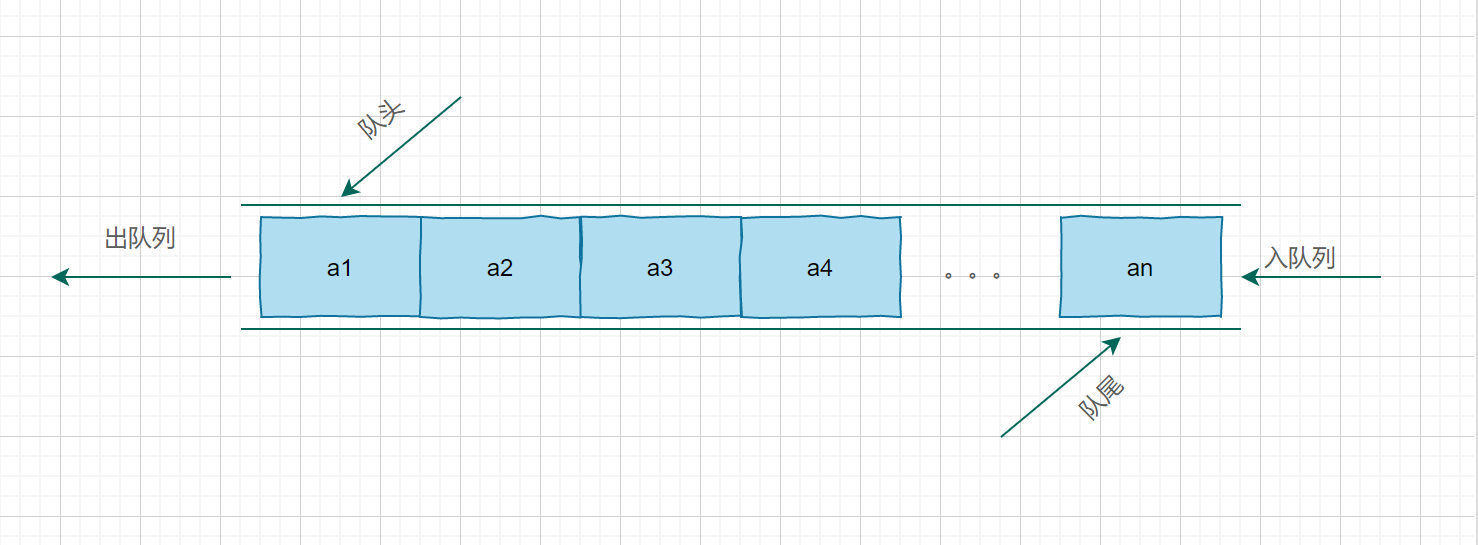
像栈一样,队列(queue)也是表。然而使用队列时插入在一端进行而删除在另一端进行,遵守先进先出的规则。所以队列的另一个名字是(FIFO)。
|
||||
|
||||
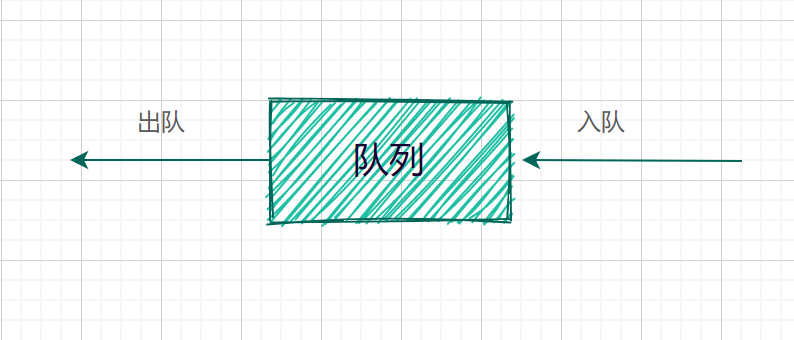
队列的基本操作是入队(enqueue):它是在表的末端(队尾(rear)插入一个元素。出队(dequeue):出队他是删除在表的开头(队头(front))的元素。
|
||||
|
||||
注:下面模型只象征着输入输出操作
|
||||
|
||||
|
||||
|
||||
具体模型
|
||||
|
||||
|
||||
|
||||
### 队列的实现
|
||||
|
||||
队列我们在树的层次遍历时经常使用,后面我们写到树的时候会给大家整理框架。队列同样也可以由数组和LinkedList实现,刷题时比较常用的方法是
|
||||
|
||||
```
|
||||
Queue<TreeNode> queue = new LinkedList<TreeNode>();
|
||||
```
|
||||
|
||||
### 循环队列
|
||||
|
||||
循环队列的出现就是为了解决队列的假溢出问题。何为假溢出呢?我们运用数组实现队列时,数组长度为5,我们放入了[1,2,3,4,5],我们将1,2出队,此时如果继续加入6时,因为数组末尾元素已经被占用,再向后加则会溢出,但是我们的下标0,和下标1还是空闲的。所以我们把这种现象叫做“假溢出”。
|
||||
|
||||
例如,我们在学校里面排队洗澡一人一个格,当你来到澡堂发现前面还有两个格,但是后面已经满了,你是去前面洗,还是等后面格子的哥们洗完再洗?肯定是去前面的格子洗。除非澡堂的所有格子都满了。我们才会等。
|
||||
|
||||
所以我们用来解决假溢出的方法就是后面满了,就再从头开始,也就是头尾相接的循环,我们把队列的这种头尾相接的顺序存储结构成为循环队列。
|
||||
|
||||
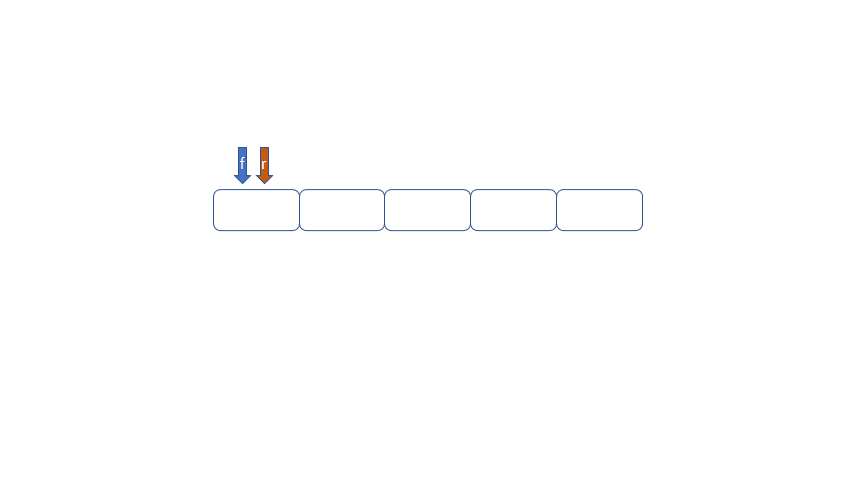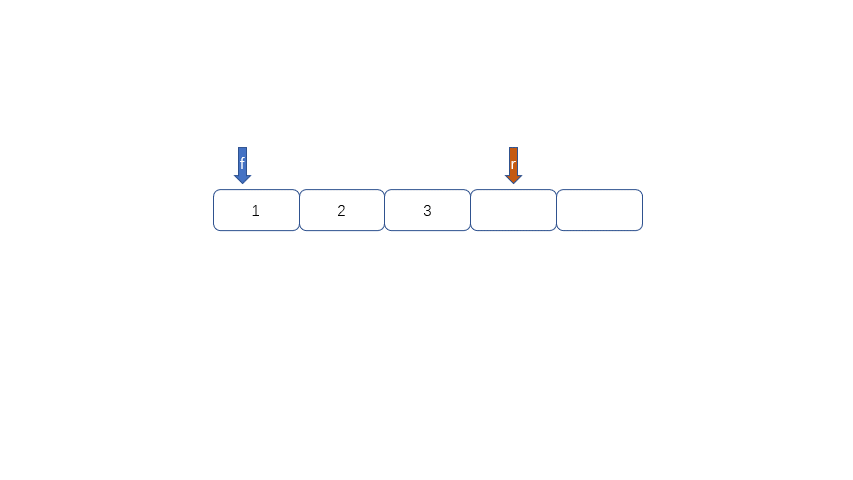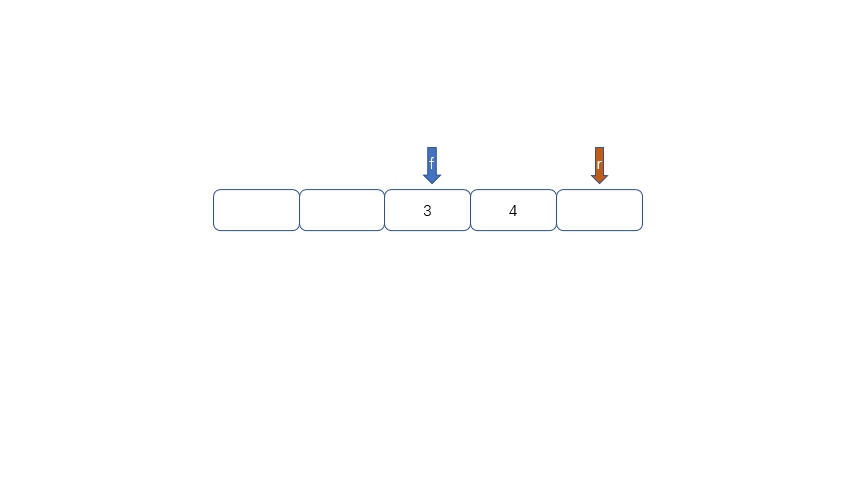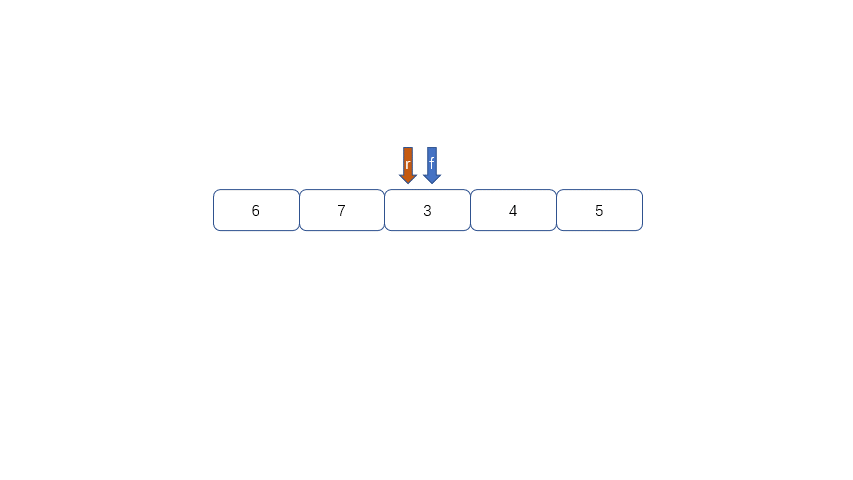
|
||||
|
||||
|
||||
|
||||
我们发现队列为空时front == rear,队列满时也是front == rear,那么问题来了,我们应该怎么区分满和空呢?
|
||||
|
||||
我们可以通过以下两种方法进行区分,
|
||||
|
||||
1.设置标记变量flag;当front==rear 时且flag==0时为空,当front==rear且rear为1时且flag==1时为满
|
||||
|
||||
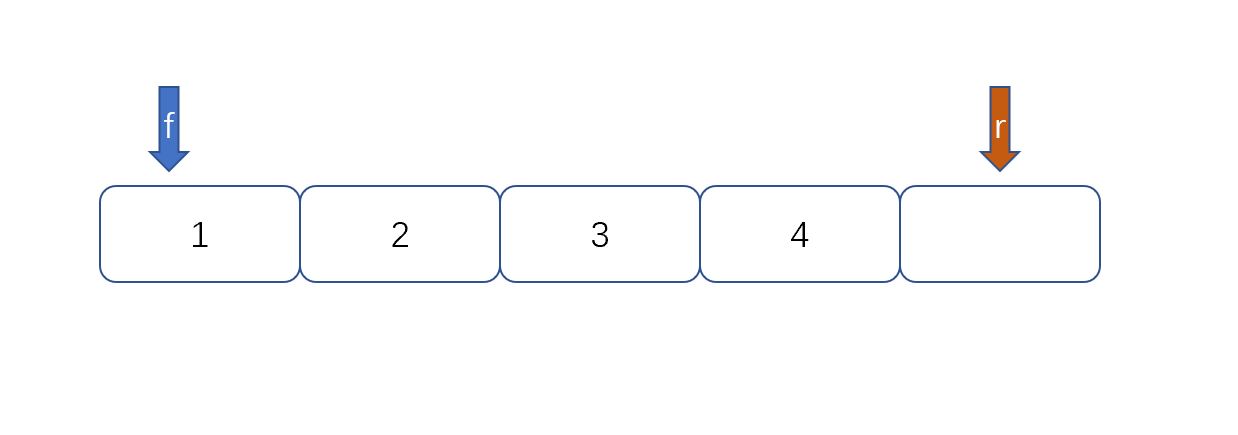
2.当队列为空时,front==rear,当队列满是我们保留一个元素空间,也就是说,队列满时,数组内还有一个空间。
|
||||
|
||||
例:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
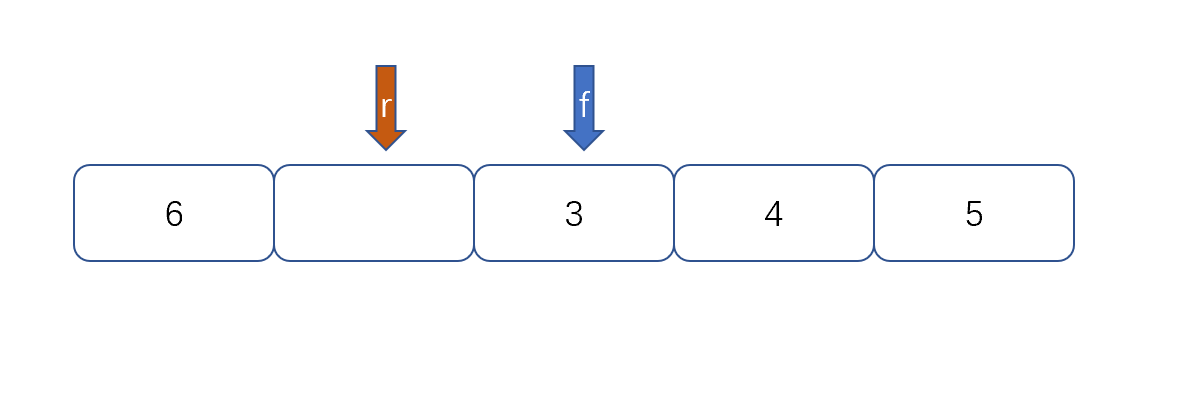
然后我们再根据以下公式则能够判断队列满没满了。
|
||||
|
||||
(rear+1)%queuesize==front
|
||||
|
||||
queuesize,代表队列的长度,上图为5。我们来判断上面两张图是否满。(4+1)%5==0,(2+1)%5==3
|
||||
|
||||
两种情况都是满的,over。
|
||||
|
||||
注:为了用动图把逻辑整的清晰明了,十几秒的动图,就要整半个多小时,改进好几遍。如果觉得图片对你有帮助的话就点个赞和在看吧。
|
||||
151
gif-algorithm/数据结构和算法/关于链表的那些事.md
Normal file
151
gif-algorithm/数据结构和算法/关于链表的那些事.md
Normal file
@@ -0,0 +1,151 @@
|
||||
# 链表详解
|
||||
|
||||
阅读完本文你会有以下收获
|
||||
|
||||
1.知道什么是链表?
|
||||
|
||||
2.了解链表的几种类型。
|
||||
|
||||
3.了解链表如何构造。
|
||||
|
||||
4.链表的存储方式
|
||||
|
||||
5.如何遍历链表
|
||||
|
||||
6.了解链表的操作。
|
||||
|
||||
7.知道链表和数组的不同点
|
||||
|
||||
8.掌握链表的经典题目。
|
||||
|
||||
### 链表的定义:
|
||||
|
||||
> 定义:链表是一种递归的数据结构,他或者为空(null),或者是指向一个结点(node)的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。
|
||||
|
||||
我们来对其解读一下,链表是一种常见且基础的数据结构,是一种线性表,但是他不是按线性顺序存取数据,而是在每一个节点里存到下一个节点的地址。我们可以这样理解,链表是通过指针串联在一起的线性结构,每一个链表结点由两部分组成,数据域及指针域,链表的最后一个结点指向null。也就是我们所说的空指针。
|
||||
|
||||
### 链表的几种类型
|
||||
|
||||
我们先来看一下链表的可视化表示方法,以便更好的对其理解。
|
||||
|
||||
- 用长方形表示对象
|
||||
- 将实例变量的值写在长方形中;
|
||||
- 用指向被引用对象的箭头表示引用关系。
|
||||
|
||||
#### 单链表
|
||||
|
||||
一个单向链表包含两个值: 当前节点的值和一个指向下一个节点的链接。
|
||||
|
||||
我们通过上面说到的可视化表示方法,构造单链表的可视化模型,如图所示。
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
#### 双向链表
|
||||
|
||||
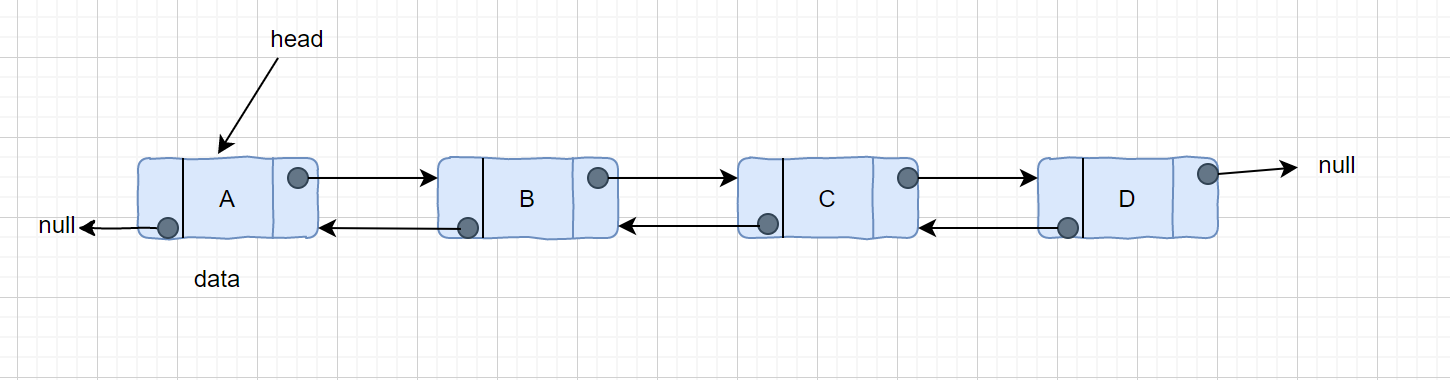
上面提到了单链表的节点只能指向节点的下一个节点。而双向链表有三个整数值: 数值、向后的节点链接、向前的节点链接,所以双链表既能向前查询也可以向后查询。
|
||||
|
||||
|
||||
|
||||
####
|
||||
|
||||
还有一个常用的链表则为循环单链表,则单链表尾部的指针指向头节点。例如在leetcode61旋转链表中,我们就是先将链表闭合成环,找到新的打开位置,并定义新的表头和表尾。
|
||||
|
||||
### 构造链表
|
||||
|
||||
java是面向对象语言,实现链表很容易。我们首先用一个嵌套类来定义节点的抽象数据类型
|
||||
|
||||
```java
|
||||
private class Node {
|
||||
Item item;
|
||||
Node next;
|
||||
}
|
||||
```
|
||||
|
||||
现在我们需要构造一条含有one,two,three的链表,我们首先为每个元素创造一个节点
|
||||
|
||||
```java
|
||||
Node first = new Node();
|
||||
Node second = new Node();
|
||||
Node third = new Node();
|
||||
```
|
||||
|
||||
将每个节点的item域设为所需的值
|
||||
|
||||
```java
|
||||
first.item = "one";
|
||||
second.item = "two";
|
||||
third.item = "three";
|
||||
```
|
||||
|
||||
然后我们设置next域来构造链表
|
||||
|
||||
```java
|
||||
first.next = second;
|
||||
second.next = third;
|
||||
```
|
||||
|
||||
注:此时third的next仍为null,即被初始化的值。
|
||||
|
||||
### 链表的存储方式
|
||||
|
||||
我们知道了如何构造链表,我们再来说一下链表的存储方式。
|
||||
|
||||
我们都知道数组在内存中是连续分布的,但是链表在内存不是连续分配的。链表是通过指针域的指针链接内存中的各个节点。
|
||||
|
||||
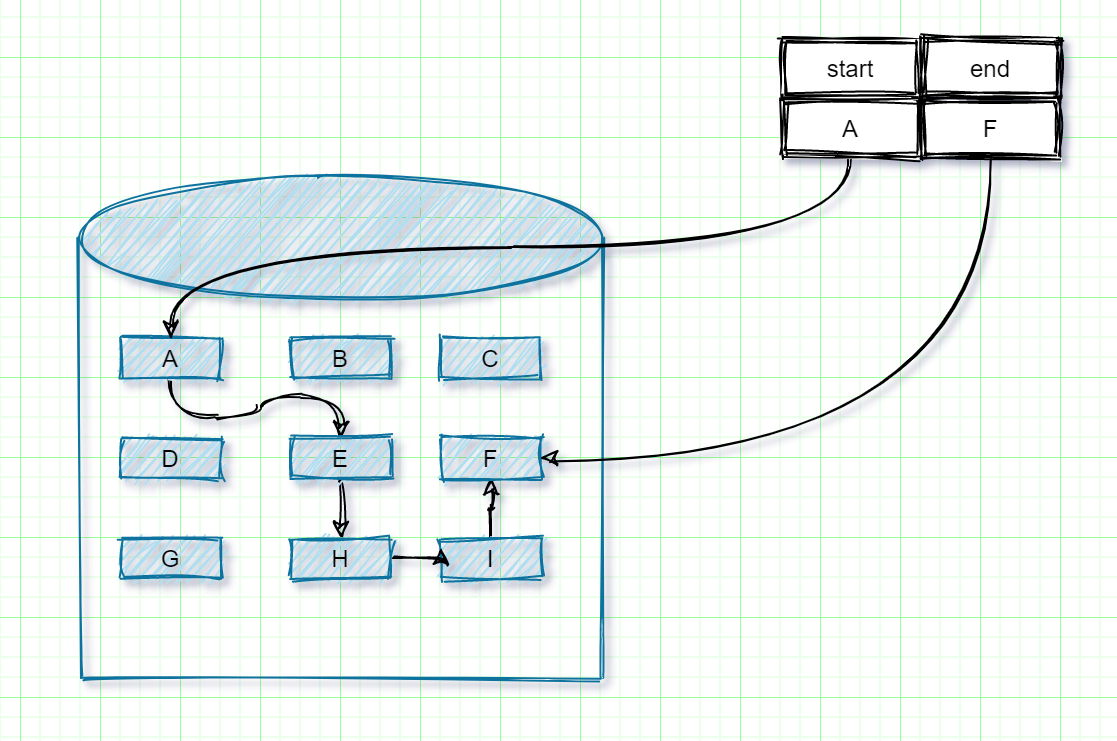
所以链表在内存中是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。我们可以根据下图来进行理解。
|
||||
|
||||
|
||||
|
||||
### 遍历链表
|
||||
|
||||
链表的遍历我们通常使用while循环(for循环也可以但是代码不够简洁)下面我们来看一下链表的遍历代码
|
||||
|
||||
for:
|
||||
|
||||
```java
|
||||
for (Node x = first; x != null; x = x.next) {
|
||||
//处理x.item
|
||||
}
|
||||
```
|
||||
|
||||
while:
|
||||
|
||||
```
|
||||
Node x = first;
|
||||
while (x!=null) {
|
||||
//处理x.item
|
||||
x = x.next;
|
||||
}
|
||||
```
|
||||
|
||||
### 链表的几种操作
|
||||
|
||||
#### 添加节点
|
||||
|
||||
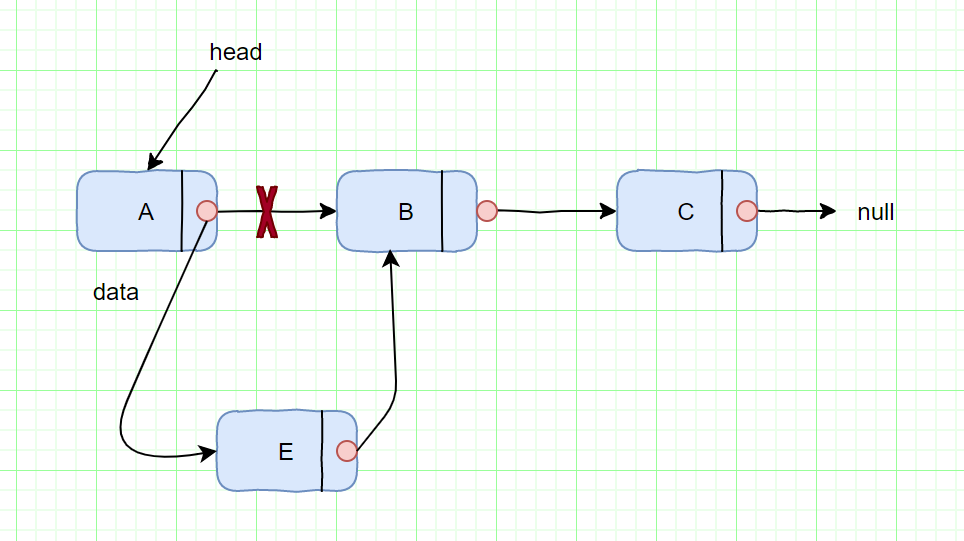
|
||||
|
||||
|
||||
|
||||
#### 删除节点
|
||||
|
||||
删除B节点,如图所示
|
||||
|
||||
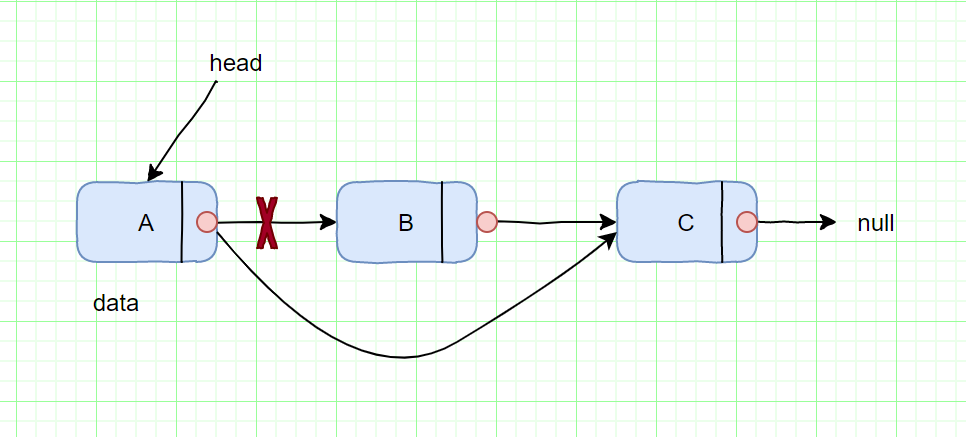
|
||||
|
||||
我们只需将A节点的next指针指向C节点即可。
|
||||
|
||||
有的同学可能会有这种疑问,B节点这样不会留着内存里吗?java含有自己的内存回收机制,不用自己手动释放内存了,但是C++,则需要手动释放。
|
||||
|
||||
我们通过上图的删除和插入都是O(1)操作。
|
||||
|
||||
链表和数组的比较
|
||||
|
||||
| | 插入/删除操作(时间复杂度) | 查询(时间复杂度) | 存储方式 |
|
||||
| ---- | ------------------------- | ------------------ | ------------ |
|
||||
| 数组 | O(n) | O(1) | 内存连续分布 |
|
||||
| 链表 | O(1) | O(n) | 内存散乱分布 |
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user