mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2026-03-10 11:54:43 +00:00
test
This commit is contained in:
172
gif-algorithm/一些分享/区块链详解.md
Normal file
172
gif-algorithm/一些分享/区块链详解.md
Normal file
@@ -0,0 +1,172 @@
|
||||
最近总是能在一些网站上看到比特币大涨的消息,诺,这不都涨破20000美元啦。
|
||||
|
||||
最近比特币涨势喜人,牵动着每一位股民的心,持有的老哥后悔说当时我咋就没多买点呢,不然明天早饭又能多加个鸡蛋啦,没持有的呢,就在懊恼后悔当时为啥就没买入呢?这不我女朋友也看到新闻了,说比特币最近涨那么厉害,咱们要不买两个呀!然后这个总是听到的比特币到底是什么东西呀?
|
||||
|
||||
你说那个比特币呀,我也不是很懂,知道一点点,我给你讲一下我知道的吧。
|
||||
|
||||
**注:本文和股票无关,单纯的介绍一下比特币原理,投资有风险,入场需谨慎**
|
||||
|
||||
> 关键词 :比特币,去中心化,挖矿,区块链,双重支付,最长链原则,工作量证明
|
||||
|
||||
我先给你说一下比特币的历史吧。
|
||||
|
||||
> 2008年爆发全球金融危机,同年11月1日,一个自称中本聪(Satoshi Nakamoto)的人在P2P foundation网站上发布了比特币白皮书《比特币:一种点对点的电子现金系统》 陈述了他对电子货币的新设想——比特币就此面世。2009年1月3日,比特币创世区块诞生。
|
||||
|
||||
你平时不是会把每天的收入和支出记在自己的小本本上,我们称之为记账。我们平常在消费的时候,银行也会为我们记录这条交易记录及交易后银行卡里的余额。然后我们会通过银行卡里数字来评估自己拥有的财富。所以我们拥有多少财富都通过银行的记账本来决定的。
|
||||
|
||||
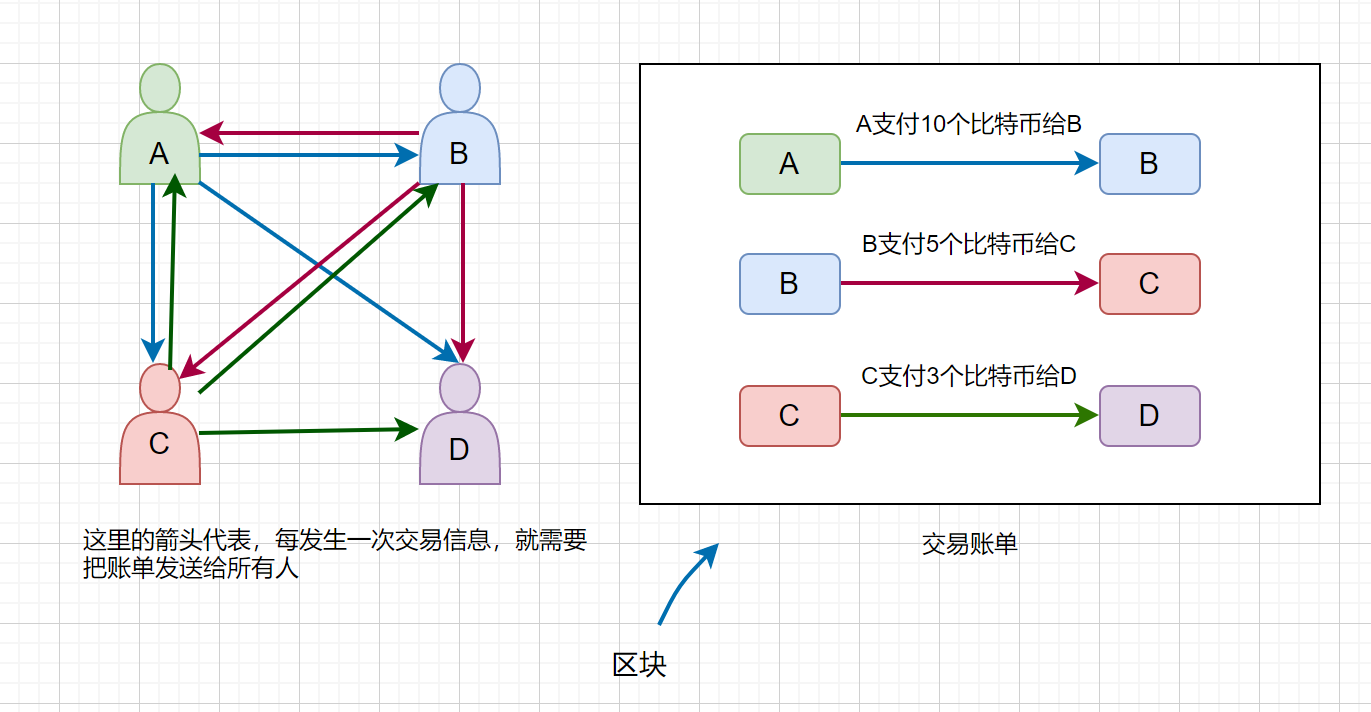
**中本聪**在**2008**年提出,其实我们可以不需要一个**中心化**的记账系统,不需要以某个人或者机构为中心来帮我们记账,我们可以**去中心化**,每一个人的账本都是透明公开的,这就叫做**去中心化电子记账系统**。下面我们通过一个例子来进行描述。
|
||||
|
||||
|
||||
|
||||
### 1.那你说的那个区块链到底是什么东西呀,我不是很懂哎?
|
||||
|
||||
我们对上图进行解析,A,B,C,D,四个小伙伴进行交易,首先 A 支付 5 个比特币给 B,那么他需要将这条交易信息发送给每位小伙伴,同理 B 和 C,C 和 D的交易也要传送给所有的小伙伴,用户会将这些交易信息记录下来,并打包成块,我们称之为**区块**,(区块大小约为1M,约4000条左右交易记录),当块存满时我们将这个块接到以前的交易记录上,形成一条链,过一段时间再把新的块接到它后面,我们称这条链为**区块链**,如下图。
|
||||
|
||||

|
||||
|
||||
|
||||
好啦,我们大概了解什么是区块链了。
|
||||
|
||||
### 2.好啦我知道什么是区块链了,但是那些用户为什么要记录交易信息呢?
|
||||
|
||||
记账奖励:每个用户都可以去记账,如果某个用户进行记帐则会奖励他一些手续费,比如A 和 B 交易 10 个比特币,A 就需要多支出一点点给为其记录的人。其实现实生活中,我们使用银行卡时也会有手续费,这里的手续费是支付给银行。
|
||||
|
||||
打包(将交易记录打包成块)奖励:打包者只能有一位,完成打包的那一位能够获得**打包奖励**,
|
||||
|
||||
### 3.哦,知道了,那打包一次能获得多少奖励呢?
|
||||
|
||||
2008年刚提出这个系统时,奖励方案如下
|
||||
|
||||
每十分钟打一个包,最开始的时候,每打一个包会奖励打包者 50 个比特币,过了四年之后,每打一个包奖励 25 个比特币,再过四年的则奖励 12.5个比特币,以此类推。
|
||||
|
||||
### 4.哇,那么多,那世界上一共有多少个比特币呢?
|
||||
|
||||
一个包奖励 50 个比特币,一个小时 6 个包,一天 24 小时,一年 365天 ,每隔四年减半,则计算公式如下
|
||||
|
||||
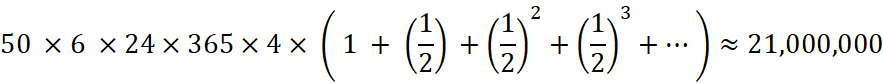
|
||||
|
||||
总数大概为 2100万个比特币。
|
||||
|
||||
### 5.因为我们有手续费和打包费的奖励机制,所以大家都抢着打包,但是打包者只能有一个人,那么我们应该让谁打包呢?
|
||||
|
||||
中本聪提出了一个**工作量证明**的办法,说白了就是想打包的用户都要去做一个很难的数学题,谁先做出来,谁就能获得这个打包的权力。打包者就能够获得奖励,但是这个题目很特别,就是我们任何人都不能用脑子把他做出来,我们只能一个数一个数的去尝试,直到你把这个数尝试出来,那么你就获得了奖励,这个过程就是我们经常说的挖矿。
|
||||
|
||||
### 6.你说的那个挖矿的原理是怎样的呢,我想不通?
|
||||
|
||||
刚才我们说挖矿的原理其实是让我们做一道数学题,谁先做出来算谁的,这个题目还不拼智商,需要我们一个一个的试,取决于咱们CPU的运行速度。那么具体原理是什么呢?
|
||||
|
||||
**这里可以选择性阅读,不感兴趣可以直接跳到第 8 个问题**
|
||||
|
||||
介绍原理之前,我们先来了解一下哈希函数,大家可以去看一下我之前之前的文章《[学生物的女朋友都能看懂的哈希表总结!](http://mp.weixin.qq.com/s?__biz=Mzg3NDQ2NDY3MA==&mid=2247486429&idx=1&sn=449b0482f89a4b2778cbd5c5d6dcc67f&chksm=ced11f2cf9a6963ab9ce6331c4bec69775e347ef03e4bae46e93113f6e99d18c83f45359a04c&scene=21#wechat_redirect)》,里面对哈希函数做出了简要描述。下面我们再来了解一下数字摘要。
|
||||
|
||||
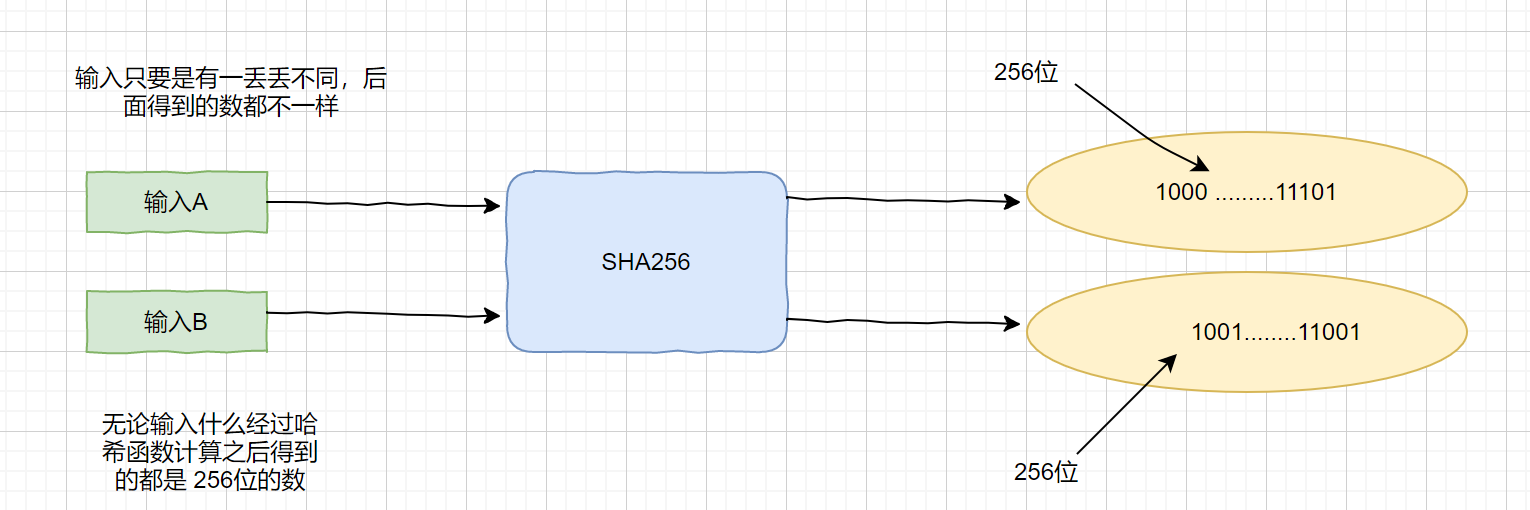
数字摘要就是采用**单向 Hash 函数**将需要加密的明文“摘要”成一串固定长度的密文这一串密文又称为数字指纹,它有固定的长度,而且不同的明文摘要成密文,其结果总是不同的,而同样的明文其摘要必定一致。
|
||||
|
||||
通俗点说就是,一个字符串,我们通过 hash 函数计算,得到一个固定长度的密文,不同的字符串得到的密文不同,哪怕仅仅是两个字符串相差一个 0 最后的得到的密文也可能完全不同,相同的字符串会得到相同的密文。通过明文得到密文很容易,我们通过特定的哈希函数就可以,但是反过来是极其难的。
|
||||
|
||||
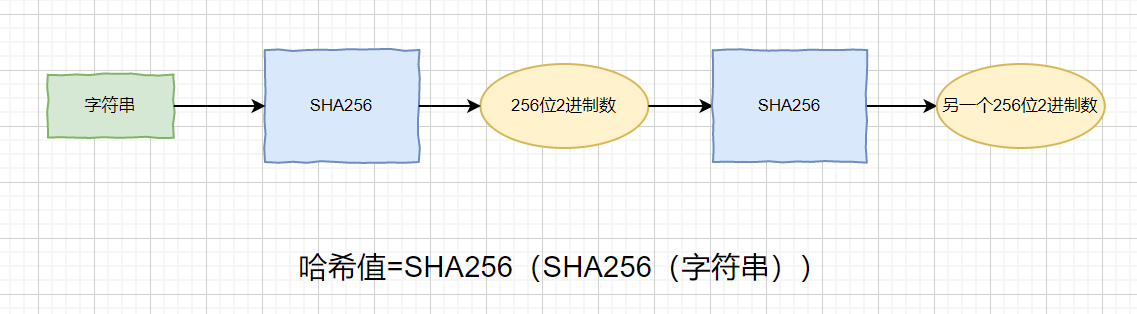
下面我们简单描述一下 著名的哈希函数 SHA256 的生成摘要的过程
|
||||
|
||||
|
||||
|
||||
|
||||
我们已经了解了生成摘要的过程,那么挖矿的具体原理是什么样呢?
|
||||
|
||||
刚才我们说到,区块链其实是一大堆交易信息,其实我们的区块里面不只有交易信息,还有头部。目前有很多人记录了系统的交易信息,然后想把自己记录的交易信息打包成块,并连接到区块链上,获得打包费。那么多人想打包,但是只能有一个人可以获得打包权,那么具体是解决了怎样的数学问题获得打包权的呢?
|
||||
|
||||
刚才我们描述了生成密文过程,那么我们的明文,也就是输入字符串,在这里主要由什么组成呢?
|
||||
|
||||
字符串 :**前块头部 + 账单的信息 + 时间 + 随机数**
|
||||
|
||||
主要有以上信息组成,前块的头部,你所记录的账单信息,时间戳,随机数组成。那么我们看,这里的组成部分对于所用用户来说,只有前块头部是固定的,账单信息因为每个人记录顺序不同也是不固定的,每个人开始的时间不一样,那么时间也是不固定的,随机数也不固定,那么既然我们的输入都是不固定的,那这个题应该怎么答呀,那怎么保证公平呢?主要通过以下方法
|
||||
|
||||
刚才我们也说了,经过 SHA256 加密之后会得到一个 256位的二进制数。
|
||||
|
||||
获得打包权的那个难题就是让我们把字符串经过两次 SHA256 运算之后得到一个哈希值,哈希值要求**前 n 位**为0,意思就是谁先算出那个前 n 位为 0 的哈希值,谁就能获得打包权。
|
||||
|
||||
因为每个人的输入是不固定的,但是对于个人来说,他开始运算的时间是固定的,头部也是固定的,他所记录内容也是固定的,所以他只能依靠调整**随机数**来修改最后的哈希值,只能挨个试,但是如果人品爆发可能试的第一个数就能得到符合要求的哈希值,但是总的来说还是一个考察算力的题目。
|
||||
|
||||
|
||||
|
||||
### 7.那哈希值前 n 位为 0 ,这个 n 是依据什么决定的呢?
|
||||
|
||||
这个 n 越大计算难度就越大,因为我们不能反算,只能挨个去试,每一位上出现 0 或 1 的概率都为 1/2,那么我们获得前 n 位为 0 的哈希值概率也就是 1/2 的 n 次方。
|
||||
|
||||
当时中本聪在设计时,为了保证每十分钟出一个块,所以就会适当的调整 n, 比特币系统每过2016个区块之后,就会自动调整一次难度目标。如果上一个难度目标调整周期(也就是之前2016个区块),平均出块时间大于10分钟,说明挖矿难度偏高,需要降低挖矿难度;反之,前一个难度目标调整周期,平均出块时间小于10分钟,说明挖矿难度偏低,需要提高挖矿难度。难度目标上调和下调的范围都有4倍的限制。
|
||||
|
||||
所以这个 n 是根据挖矿难度(算力)进行调整的,也就是我们矿机的算力和矿机数量等进行调整。
|
||||
|
||||
### 8.哦,我懂了,那如果有人冒充咱们咋办,偷偷花咱们的比特币!
|
||||
|
||||
这个问题问的好
|
||||
|
||||
说到防止假冒,我们先来说一下身份认证,身份验证又称“验证”、“鉴权”,是指通过一定的手段,完成对用户身份的确认。指纹,人脸,签名等都是传统的认证手段,另外我们说一下比特币系统的电子签名。
|
||||
|
||||
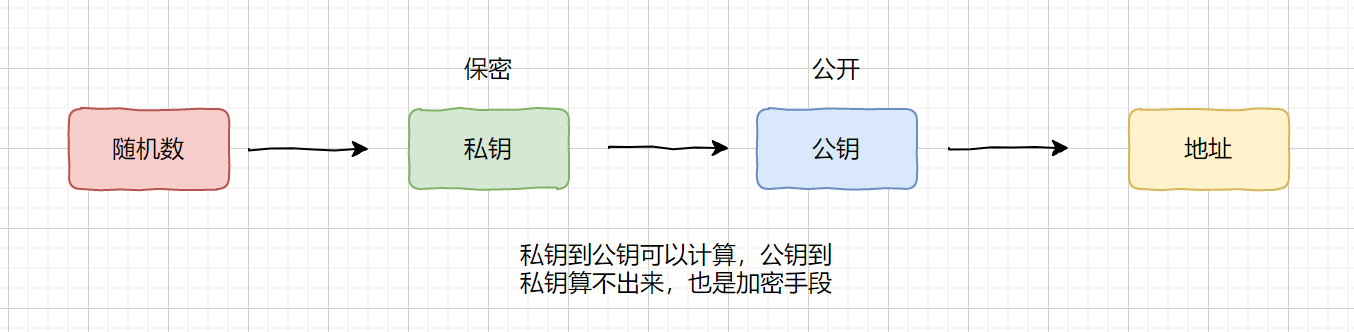
比特币用户在注册时会生成一个随机数,通过随机数会产生一个私钥的字符串,这个私钥又可以产生一个公钥字符串和地址,私钥和公钥是对应的,并且私钥是保密的,别人向你交易时,你只需要把你的地址发过去即可,如果你给别人交易时,则需要将你的公钥和地址一起发过去。流程图如下
|
||||
|
||||
|
||||
|
||||
我们在传输记录时通过私钥加密,然后通过公钥解密,加密和解密的钥匙不一样,所以我们称之为非对称加密
|
||||
|
||||
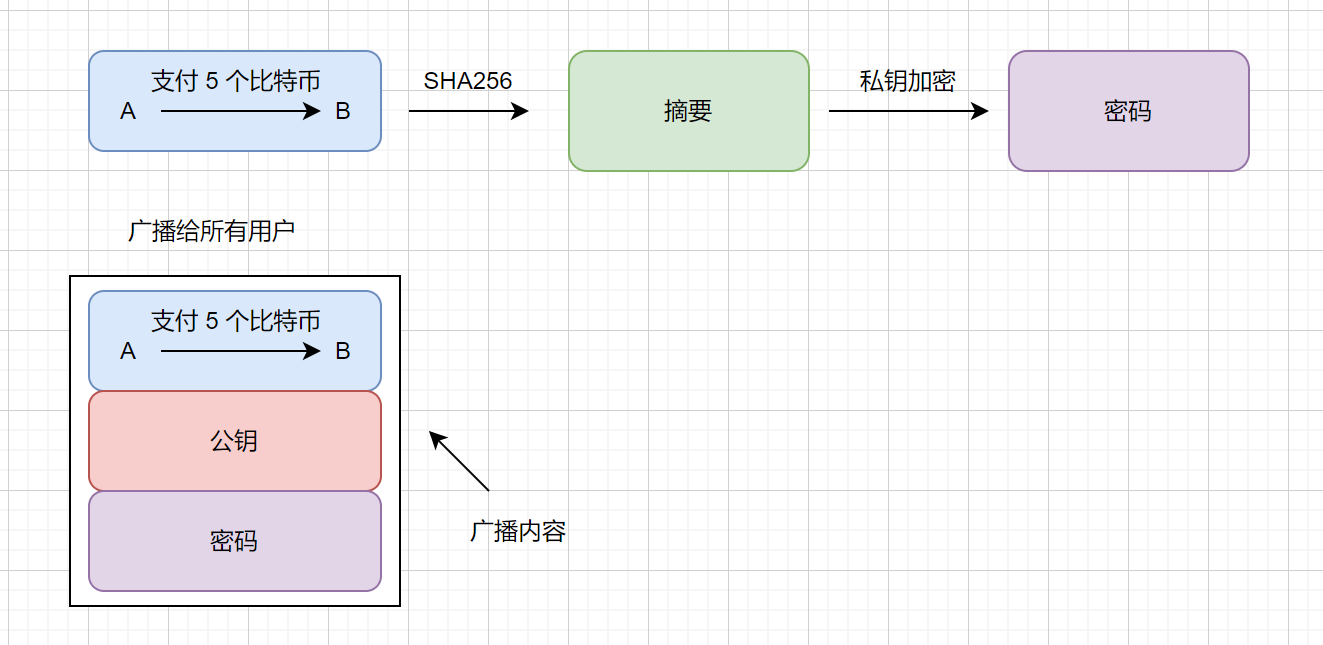
具体交易流程如下,例 A支付 5 个比特币给 B
|
||||
|
||||
|
||||
|
||||
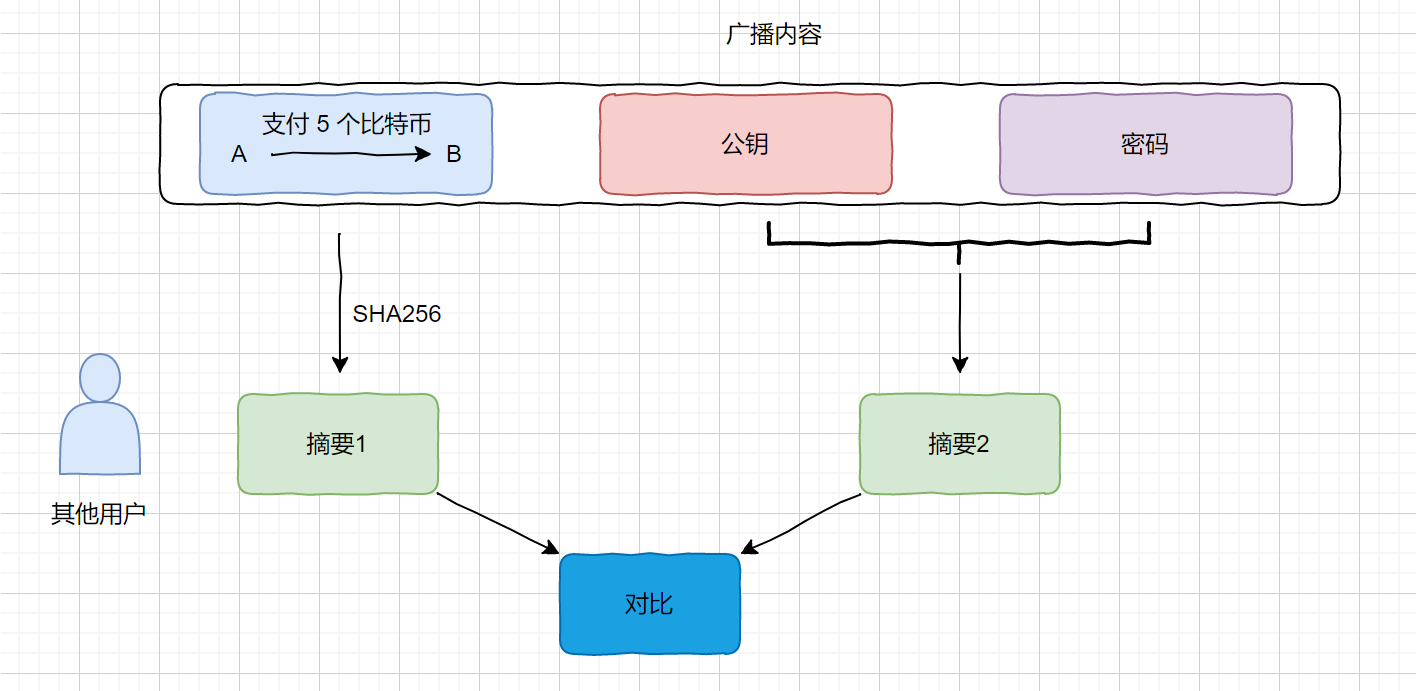
我们其他用户接收到了这个支付消息,那其他用户怎么判断这条信息是不是A发出的呢?不是他人冒充 A 发的呢?具体流程如下
|
||||
|
||||
|
||||
|
||||
其他用户进行对比,如果一致则认可这条消息是A发的,不一致则认为是别人冒充,所有用户则会拒绝这条消息。这里可能会不明白了,公钥和私钥你都发出来了解密肯定的呀,刚才我们说公钥的公开的,但是公钥是由私钥加密得到的,私钥是私密的唯一的,只有 A 用户知道自己的私钥。
|
||||
|
||||
### 9.哇,好神奇啊,我知道了,那要是我只有 5 个比特币,同时支付给两个人咋办,每个人五个,那我岂不是赚了呀。
|
||||
|
||||
厉害呀,这你都能想到,但是你想多啦。
|
||||
|
||||
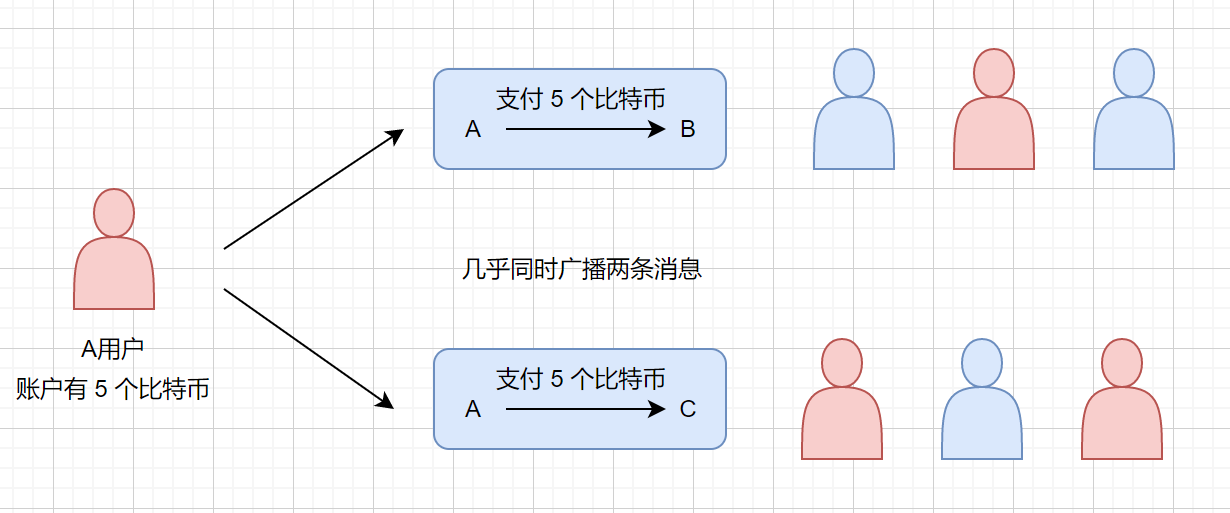
比如A只有五个比特币,他同时发了两个消息,分别是给 B 五个比特币,给 C 五个比特币,但是他总数只有 5 个,这样显然是不行的,我们称之为**双重支付**。
|
||||
|
||||
那么我们如何解决呢?
|
||||
|
||||
##### 余额检查
|
||||
|
||||
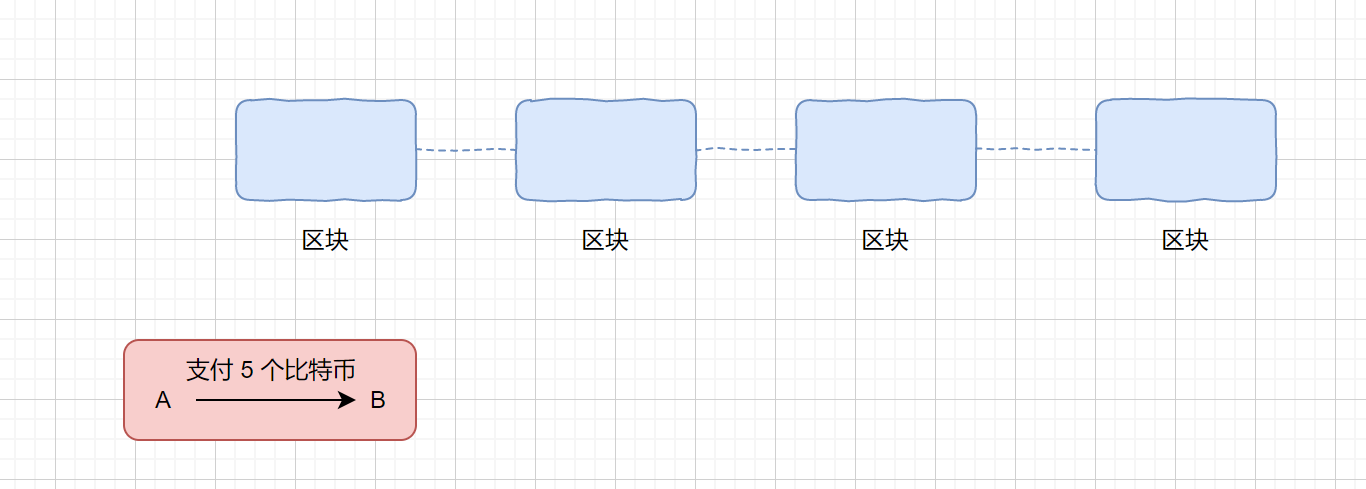追溯
|
||||
|
||||
用户在接收到这个消息时,会先从区块链里,进行查询A的交易记录,得出A的余额是否大于交易数额,如果大于则接收,反之则拒绝。
|
||||
|
||||
##### 解决双重支付
|
||||
|
||||
首先我们来了解下什么是双重支付,打个比方哈,袁记菜馆第963家分店因为店长经营不善,要进行出售,出售的时候店长将这个房子同时卖给了两个人,但是只有一个房子,这就是**双重支付**。
|
||||
|
||||
双重支付
|
||||
|
||||
在比特币系统中是如何解决双重支付问题的呢?我们 A 用户只有 5 个比特币,但是他几乎同时发布了两条广播,此时有些用户会先接收到第一条广播,然后进行追溯,发现 A 只有5个比特币,则会拒绝第二条。同理先接收到第二条广播的用户也会如此。就好比形成了两个阵营,然后两个阵营的用户进行答题,然后获得了打包权,则会将自己打的包接到区块链上,那么他所接收到的那条消息则会被整个系统认可。另一条则会放弃。
|
||||
|
||||
比如用户 D 先接收到了第二条广播 ,A 支付给 C,然后 D 用户获得了打包权,则 D 将包接到链上,那么其余用户则会放弃自己的包,全部都认可 D 所记录的交易信息。所以此时 C 收入 5 个比特币,B 没有收入。所以我们接收到别人交易消息时,不能认为当时已经到账,要等新的块已经形成,消息被记录到主链上才可以。
|
||||
|
||||
### 10.那如果有人偷偷篡改交易信息,那他不就成比特币最多的人了吗?
|
||||
|
||||
想的挺全面呀,厉害呀你
|
||||
|
||||
我们考虑一下这种情况,A 已经支付给了 B 五个比特币,但是他想把这个记录删掉,伪造一下记录。有这种可能吗?
|
||||
|
||||
说之前我们先来描述一下比特币系统遵循的**最长链原则**,那什么是最长链原则呢?
|
||||
|
||||
最长链
|
||||
|
||||
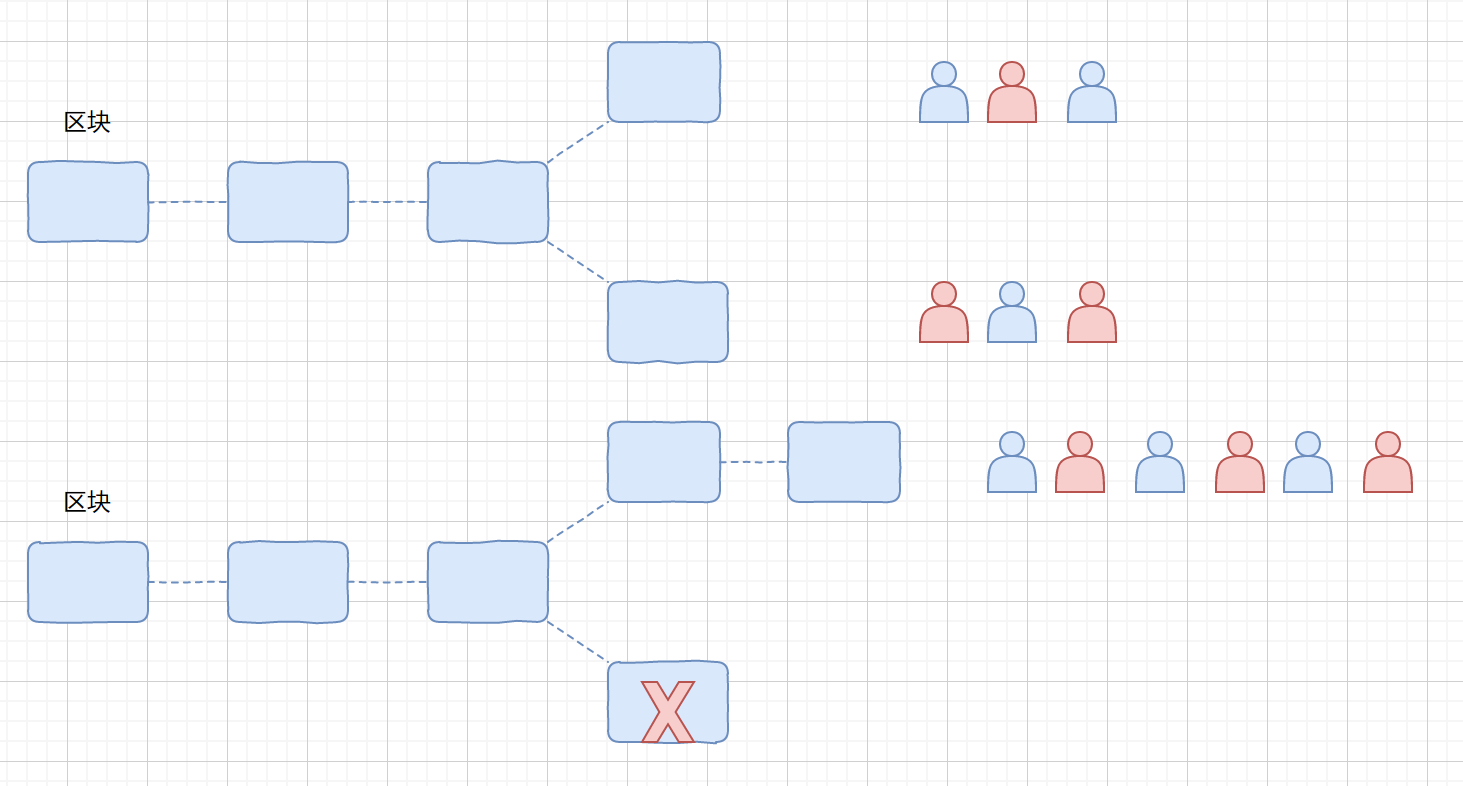
比如上图,我们同时有两个块接到了链上,那么会有两拨人,他们都会以第一个接收到的块为准,然后两拨人继续运算,当某一拨中的某个人获得打包权之后则会将新块接到他接收的块后面,那么此时他的这个链是整个系统最长的链,则会被所有人认可,另一拨人也会来到这个最长链下面继续打包。之前的那个分支则会废弃。如果说某个人他就不想转移阵容,非得死守那个相对短的链,这样也是可以的,只要你一己之力可以对抗所有人,把你这个链变成最长链,大家则会都认可你这条链。
|
||||
|
||||
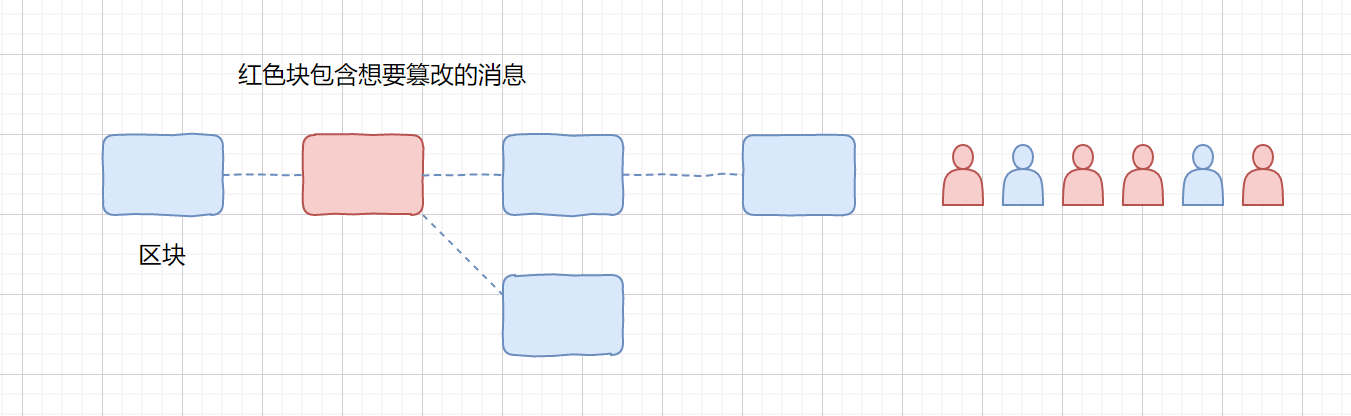
那么我们来说一下,如何防止篡改
|
||||
|
||||
|
||||
|
||||
|
||||
A 此时想要修改红色块里的交易记录,则 A 需要重新计算重新打包,创造出一个支链来,但是大家不会承认你这个支链,因为这个支链不是最长的,所以不会承认你伪造的信息,如果你非要继续往下算,什么时候你自己创造的支链长度大于世界上所有人的打包的链的长度,那么恭喜你,你伪造成功了,大家都认可你的伪造信息了,所以说理论上是可以篡改的,但是你改了之后不会被大家承认,除非你的计算能力超过了世界上其余所有的人。大家试想一下一个掌握全世界一半以上算力的人,会去干这种无聊的事吗?
|
||||
|
||||
这下我全都懂了,那咱们快去买两个吧!
|
||||
|
||||
你看看现在一个多少钱啦,买不起呀咱们。
|
||||
|
||||
<u></u>
|
||||
|
||||
另外给大家建了一个寒假刷题互相监督群,需要的可以联系我,公众号内点击一起刷题即可,为了防止广告党进入,大家记得备注【刷题】,目前人数大概有200来人。大家可以自行组成小队,也可以一起商量题目。多个人一起走,才能走得更远
|
||||
|
||||
|
||||
|
||||
|
||||
101
gif-algorithm/一些分享/学习.md
Normal file
101
gif-algorithm/一些分享/学习.md
Normal file
@@ -0,0 +1,101 @@
|
||||
不知道各位有没有遇到过下面这种情况
|
||||
|
||||
每天早上醒来,先给自己打个气,今天我一定要好好学习。打完气之后,就开始躺在床上玩手机。吃了睡,睡了吃,好不容易打开电脑学个习,看了半个小时就再次倒下。
|
||||
|
||||
还有的时候呢?2:45啦,我再玩一会吧,凑个整,到 3 点再学习,玩着玩着,那边你妈喊你吃晚饭了。
|
||||
|
||||
晚上,躺在床上,再一次给自己打气,我明天一定要早起好好学习,然后一个没忍住继续玩手机,第二天又睡过头了,继续复制昨天的生活。
|
||||
|
||||

|
||||
|
||||
相信大家放假之前都有在假期里大干一场的想法,可谁知回到家之后,身体开始不受控制,总想躺着。给大家总结了一波小技巧,希望对大家有一丢丢帮助。
|
||||
|
||||
**拒绝舒适**
|
||||
|
||||
**换掉睡衣**,或许我们不能好好学习的**罪魁祸首之一**就是身上的睡衣,行为影响态度,如果我们穿着睡衣葛优躺在沙发上的时候,我们就倾向于刷刷视频,找朋友开开黑,做一些放松的活动。但是如果你**穿上上学的衣服**,甚至说穿上校服,你离学习就更近一些,**更容易进入到类似于学校的学习状态**,**成为一个没有感情的学习机器。**
|
||||
|
||||
**欺骗自己**
|
||||
|
||||
有的时候我们好不容易坐到电脑前,然后我们开始纠结,翻两下书又开始背单词,事情太多,先做哪个呢?
|
||||
|
||||
要不还是先看会手机吧,总的来说就是**计划太多,无从下手,犹豫太久,啥也没有**。**重要的不是学什么,而是学。**
|
||||
|
||||
对我们来说更难的不是继续做,而是开始做。就比如我们**离开舒适区**,进入书房,坐在电脑前敲下第一行代码的过程,往往比我们已经开始,继续行动,要难很多很多,所以**我们可以欺骗自己,我就学十分钟,只听一节网课,只做一道算法题,总的来说就是先开始再说。**
|
||||
|
||||
**然后刚开始学习时我们可以先做些简单的工作,提高我们的学习积极性,**帮助我们进入学习状态,**循序渐进**。如果刚一开始就做些困难工作,我们内心会对其抗拒,渐渐失去对学习的耐心。
|
||||
|
||||
**整齐的学习环境**
|
||||
|
||||
一个整齐的学习环境能让你。。。算了,这个我也没做到,不说了,反正还是整洁一点好。
|
||||
|
||||
**学会休息**
|
||||
|
||||
个人认为这一点格外重要,在家里同样需要管理好作息,管理作息不一定非要起的特别早来学习,而是**保持一个较规律的作息习惯**。你可以给自己**设定一个睡觉时间和起床时间**,完全按照这个时间执行。这样你前一天做好的规划就不会被打乱。
|
||||
|
||||
告诉大家一个我经常用的小窍门,那就是**不躺在床上玩手机,看手机的时候坐在桌子旁,到了睡觉时间,则把手机放在桌子上,躺到床上迅速入睡**。那么你的起床时间和睡觉时间就能得到保证。因为我们**晚睡晚起的大多数情况都是赖床玩手机。**
|
||||
|
||||
我们被闹钟吵醒之后肯定还是很困,可能会关掉桌子上的闹钟继续睡觉,这时我们可以**做几个俯卧撑,听听音乐**,就会让你困意全无。起床成功。
|
||||
|
||||
**制定任务清单**
|
||||
|
||||
在前一天晚上**按照轻重缓急**制定第二天的任务清单,第二天我们就可以直接按照任务清单进行工作,这样能让你快速进入学习状态。
|
||||
|
||||
另外我建议大家尽量将**任务拆解细化**,因为我们大脑在面对庞大的工作时内心是拒绝的,**任务量越大,我们越难开始行动**,所以我们**将任务拆解细化之后,更容易让我们开始做**。其实很多时候我们迷惑的不是怎样继续当下的学习任务,而是怎样开始当下的学习任务。
|
||||
|
||||
**不要用时间做计划**
|
||||
|
||||
因为我们是在家里学习,**没有学校那么严格的束缚**,这时我们该想着那我得自己约束自己呀,今天我要学习六个小时,明天七个,后天八个。但是结果是这样的吗?
|
||||
|
||||
**帕金森定理:只要还有时间,工作就会自动地占满所有可用的时间;如果你给自己安排了充裕的时间从事一项活动,你会放慢你的节奏以使用掉所有分配的时间。**
|
||||
|
||||
当我们给我们的某一项工作规划了固定的时间之后,我们可能会出现两种情况
|
||||
|
||||
1.拖延反正还有那么多时间可以用,先玩会手机等会再做吧。
|
||||
|
||||
2.痛苦比如我们给自己规划了今天要学 6 个小时,这时我们可能就在想,哇,今天还有六个小时要学,好煎熬,这样或许就**会打击我们学习的积极性**,总之我们不要低估我们拖延的能力,你会发现自己真的很牛批。
|
||||
|
||||
更好的方法是**用学习量来做规划**,比如今天刷几道题,记几个单词,看几页书等,**一个清晰明确的目标或许会让我们事半功倍。**
|
||||
|
||||
既然都读到了这里,还不赶快行动起来,**快去学习吧**。
|
||||
|
||||
好啦,现在我们坐到桌子前准备学习啦,那么我们有没有遇到过这种情况呢?
|
||||
|
||||
我们学习的时候**总会走神**,一会转转笔,一会抠抠手,刷刷手机,大家**不要太自责**,这不是我们一个人的问题《单核工作法》的作者说,这是人的生理本能惹的货,**大脑会鼓励我们走神**,每次我们走神之后,大脑就会获得一份多巴胺奖励,让你爽一下。
|
||||
|
||||
那么有没有什么办法帮助提升学习时的专注力呢?下面是一些小技巧希望能够帮到大家。
|
||||
|
||||
**舒缓音乐**
|
||||
|
||||
个人习惯会在工作时**听一些舒缓的音乐**,帮助我**提高专注度**,但是不一定适用所有人,大家可以试一下,另外这个歌单的名字是清华大学自习室歌单,不知道真假,俺也没去过清华,不过歌是真不错,大家可以去听一下。
|
||||
|
||||
<img src="https://pic2.zhimg.com/80/v2-ed02d6887fa21ee94815240a7c40cd9d_1440w.jpeg" alt="img" style="zoom: 25%;" />
|
||||
|
||||
**动手实践**
|
||||
|
||||
动手实践在结合我们手和脑方面非常有效,我们可以使用这种方法让自己专注,**边看书,边实践**可以带动我们的思考。比起只看书可以更好的集中我们的注意力,当我们**接受知识的速度和处理知识的速度是趋同的时候**,我们就会**忘记时间,超级专注**。
|
||||
|
||||
为啥我们看电视的时候可以一看看几个小时,忘记时间,是因为我们接收剧情的速度和大脑处理的速度是趋同的,看的时候不用思考,越看越上瘾。
|
||||
|
||||
**巧用工具**
|
||||
|
||||
大家不要排斥利用软件帮助我们学习,毕竟人都是有惰性的,我们不能控制住自己的时候,可以**使用一些工具来帮助我们**,下面我给大家介绍几个我之前读大学的时候用过的软件,个人认为是有一些帮助的。
|
||||
|
||||
<img src="https://pic4.zhimg.com/80/v2-74e41ddace28ffe7449da82bf329ae95_1440w.jpeg" alt="img" style="zoom:25%;" />
|
||||
|
||||
**软件名称:达目标**
|
||||
|
||||
这是一款**设定目标的软件**,我们可以在上面设定我们想要完成的目标,然后我们每天打卡,如果**忘记打卡的次数超过我们设定的休假天数,则会挑战失败**。失败的代价是金钱。是的,我们就失去了我们的挑战金。所以这个软件可以让我们强制打卡,毕竟钱没了还是很心疼的。我们还可以围观别人的目标,**监督别人打卡,如果他挑战失败则可以分得他的挑战金。**
|
||||
|
||||
<img src="https://pic2.zhimg.com/80/v2-cd03cec563095eb03e74880ff3bf936b_1440w.jpeg" alt="img" style="zoom:25%;" />
|
||||
|
||||
**软件名称:番茄ToDo**
|
||||
|
||||
这是一款锁机软件,我们可以用它来**强制锁机,只保留通话功能,**设定好锁机时间之后,手机就变成了一块板砖,只有等到时间结束之后,才能使用手机。如果手机**没有禅定模式**的话,则可以用这个软件代替
|
||||
|
||||
<img src="https://pic1.zhimg.com/80/v2-41cbd40c65ee96ac81768b757f024f58_1440w.jpeg" alt="img" style="zoom:25%;" />
|
||||
|
||||
**软件名称:Forest**
|
||||
|
||||
这也是一款能够**帮助我们自律**的软件,我们可以设定学习时长,**如果期间玩手机,则会让你的小树枯萎,完成目标则会让小树长大**,有点类似养成型游戏。这是同学推荐的,他经常用,听说效果还不错,感兴趣的同学可以试试。
|
||||
|
||||
好啦,我知道的大概就这么多啦,希望大家可以利用好寒假,冲冲冲!
|
||||
@@ -0,0 +1,130 @@
|
||||
> 为保证代码严谨性,文中所有代码均在 leetcode 刷题网站 AC ,大家可以放心食用。
|
||||
|
||||
皇上生辰之际,举国同庆,袁记菜馆作为天下第一饭店,所以被选为这次庆典的菜品供应方,这次庆典对于袁记菜馆是一项前所未有的挑战,毕竟是第一次给皇上庆祝生辰,稍有不慎就是掉脑袋的大罪,整个袁记菜馆内都在紧张的布置着。此时突然有一个店小二慌慌张张跑到袁厨面前汇报,到底发生了什么事,让店小二如此慌张呢?
|
||||
|
||||
袁记菜馆内
|
||||
|
||||
店小二:不好了不好了,掌柜的,出大事了。
|
||||
|
||||
袁厨:发生什么事了,慢慢说,如此慌张,成何体统。(开店开久了,架子出来了哈)
|
||||
|
||||
店小二:皇上按照咱们菜单点了 666 道菜,但是咱们做西湖醋鱼的师傅请假回家结婚了,不知道皇上有没有点这道菜,如果点了这道菜,咱们做不出来,那咱们店可就完了啊。
|
||||
|
||||
(袁厨听了之后,吓得一屁股坐地上了,缓了半天说道)
|
||||
|
||||
袁厨:别说那么多了,快给我找找皇上点的菜里面,有没有这道菜!
|
||||
|
||||
找了很久,并且核对了很多遍,最后确认皇上没有点这道菜。菜馆内的人都松了一口气
|
||||
|
||||
通过上面的一个例子,让我们简单了解了字符串匹配。
|
||||
|
||||
字符串匹配:设 S 和 T 是给定的两个串,在主串 S 中找到模式串 T 的过程称为字符串匹配,如果在主串 S 中找到 模式串 T ,则称匹配成功,函数返回 T 在 S 中首次出现的位置,否则匹配不成功,返回 -1。
|
||||
|
||||
例:
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
在上图中,我们试图找到模式 T = baab,在主串 S = abcabaabcabac 中第一次出现的位置,即为红色阴影部分, T 第一次在 S 中出现的位置下标为 4 ( 字符串的首位下标是 0 ),所以返回 4。如果模式串 T 没有在主串 S 中出现,则返回 -1。
|
||||
|
||||
解决上面问题的算法我们称之为字符串匹配算法,今天我们来介绍三种字符串匹配算法,大家记得打卡呀,说不准面试的时候就问到啦。
|
||||
|
||||
## BF算法(Brute Force)
|
||||
|
||||
这个算法很容易理解,就是我们将模式串和主串进行比较,一致时则继续比较下一字符,直到比较完整个模式串。不一致时则将模式串后移一位,重新从模式串的首位开始对比,重复刚才的步骤下面我们看下这个方法的动图解析,看完肯定一下就能搞懂啦。
|
||||
|
||||

|
||||
|
||||
**因为不可以放置视频,所以想看视频的同学,可以去看公众号原文,那里有视频**
|
||||
|
||||
通过上面的代码是不是一下就将这个算法搞懂啦,下面我们用这个算法来解决下面这个经典题目吧。
|
||||
|
||||
### leetcdoe 28. 实现 strStr()
|
||||
|
||||
#### 题目描述
|
||||
|
||||
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
|
||||
|
||||
示例 1:
|
||||
|
||||
> 输入: haystack = "hello", needle = "ll"
|
||||
> 输出: 2
|
||||
|
||||
示例 2:
|
||||
|
||||
> 输入: haystack = "aaaaa", needle = "bba"
|
||||
> 输出: -1
|
||||
|
||||
#### 题目解析
|
||||
|
||||
其实这个题目很容易理解,但是我们需要注意的是一下几点,比如我们的模式串为 0 时,应该返回什么,我们的模式串长度大于主串长度时,应该返回什么,也是我们需要注意的地方。下面我们来看一下题目代码吧。
|
||||
|
||||
#### 题目代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
int haylen = haystack.length();
|
||||
int needlen = needle.length();
|
||||
//特殊情况
|
||||
if (haylen < needlen) {
|
||||
return -1;
|
||||
}
|
||||
if (needlen == 0) {
|
||||
return 0;
|
||||
}
|
||||
//主串
|
||||
for (int i = 0; i < haylen - needlen + 1; ++i) {
|
||||
int j;
|
||||
//模式串
|
||||
for (j = 0; j < needlen; j++) {
|
||||
//不符合的情况,直接跳出,主串指针后移一位
|
||||
if (haystack.charAt(i+j) != needle.charAt(j)) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
//匹配成功
|
||||
if (j == needlen) {
|
||||
return i;
|
||||
}
|
||||
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
我们看一下BF算法的另一种算法(显示回退),其实原理一样,就是对代码进行了一下修改,只要是看完咱们的动图,这个也能够一下就能看懂,大家可以结合下面代码中的注释和动图进行理解。
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
//i代表主串指针,j模式串
|
||||
int i,j;
|
||||
//主串长度和模式串长度
|
||||
int halen = haystack.length();
|
||||
int nelen = needle.length();
|
||||
//循环条件,这里只有 i 增长
|
||||
for (i = 0 , j = 0; i < halen && j < nelen; ++i) {
|
||||
//相同时,则移动 j 指针
|
||||
if (haystack.charAt(i) == needle.charAt(j)) {
|
||||
++j;
|
||||
} else {
|
||||
//不匹配时,将 j 重新指向模式串的头部,将 i 本次匹配的开始位置的下一字符
|
||||
i -= j;
|
||||
j = 0;
|
||||
}
|
||||
}
|
||||
//查询成功时返回索引,查询失败时返回 -1;
|
||||
int renum = j == nelen ? i - nelen : -1;
|
||||
return renum;
|
||||
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@@ -0,0 +1,214 @@
|
||||
## BM算法(Boyer-Moore)
|
||||
|
||||
我们刚才说过了 BF 算法,但是 BF 算法是有缺陷的,比如我们下面这种情况
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
如上图所示,如果我们利用 BF 算法,遇到不匹配字符时,每次右移一位模式串,再重新从头进行匹配,我们观察一下,我们的模式串 abcdex 中每个字符都不一样,但是我们第一次进行字符串匹配时,abcde 都匹配成功,到 x 时失败,又因为模式串每位都不相同,所以我们不需要再每次右移一位,再重新比较,我们可以直接跳过某些步骤。如下图
|
||||
|
||||

|
||||
|
||||
我们可以跳过其中某些步骤,直接到下面这个步骤。那我们是依据什么原则呢?
|
||||
|
||||

|
||||
|
||||
### 坏字符规则
|
||||
|
||||
我们之前的 BF 算法是从前往后进行比较 ,BM 算法是从后往前进行比较,我们来看一下具体过程,我们还是利用上面的例子。
|
||||
|
||||
|
||||
|
||||
BM 算法是从后往前进行比较,此时我们发现比较的第一个字符就不匹配,我们将**主串**这个字符称之为**坏字符**,也就是 f ,我们发现坏字符之后,模式串 T 中查找是否含有该字符(f),我们发现并不存在 f,此时我们只需将模式串右移到坏字符的后面一位即可。如下图
|
||||
|
||||

|
||||
|
||||
那我们在模式串中找到坏字符该怎么办呢?
|
||||
|
||||
|
||||
|
||||
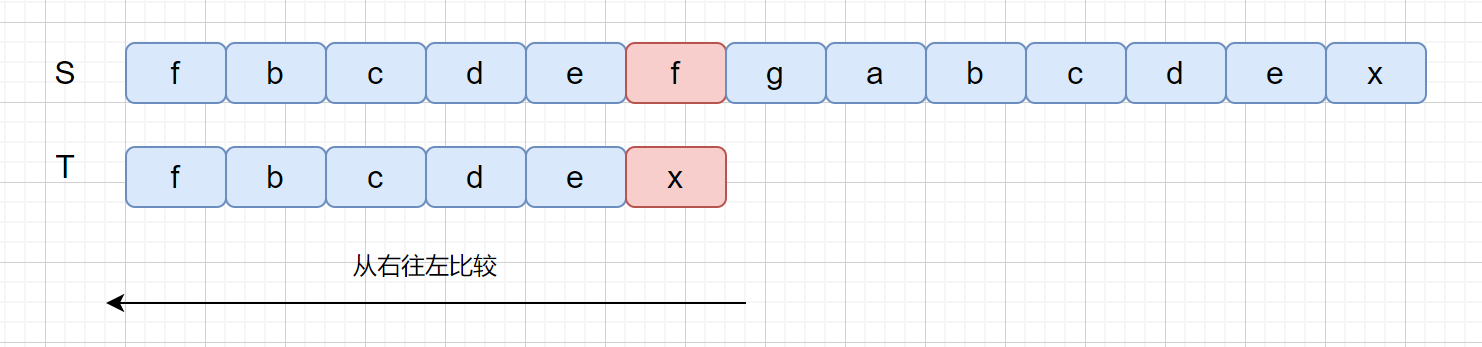
此时我们的坏字符为 f ,我们在模式串中,查找发现含有坏字符 f,我们则需要移动模式串 T ,将模式串中的 f 和坏字符对齐。见下图。
|
||||
|
||||

|
||||
|
||||
然后我们继续从右往左进行比较,发现 d 为坏字符,则需要将模式串中的 d 和坏字符对齐。
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
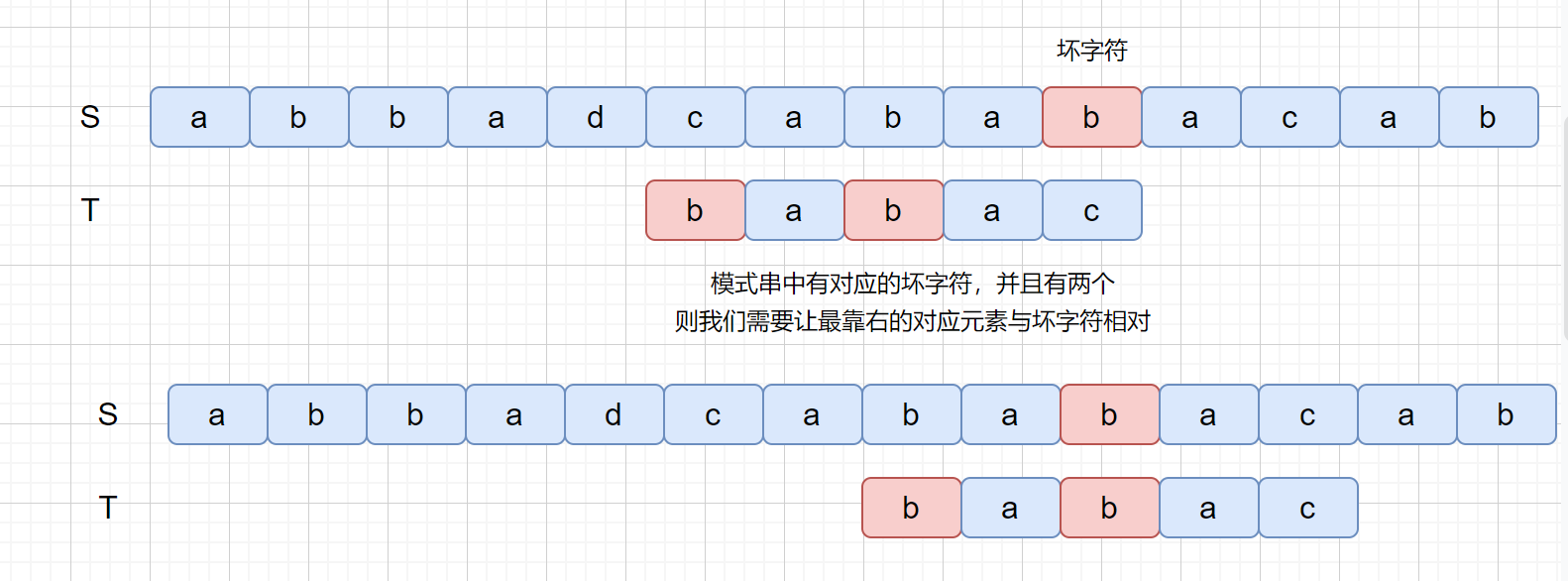
那么我们在来思考一下这种情况,那就是模式串中含有多个坏字符怎么办呢?
|
||||
|
||||
|
||||
|
||||
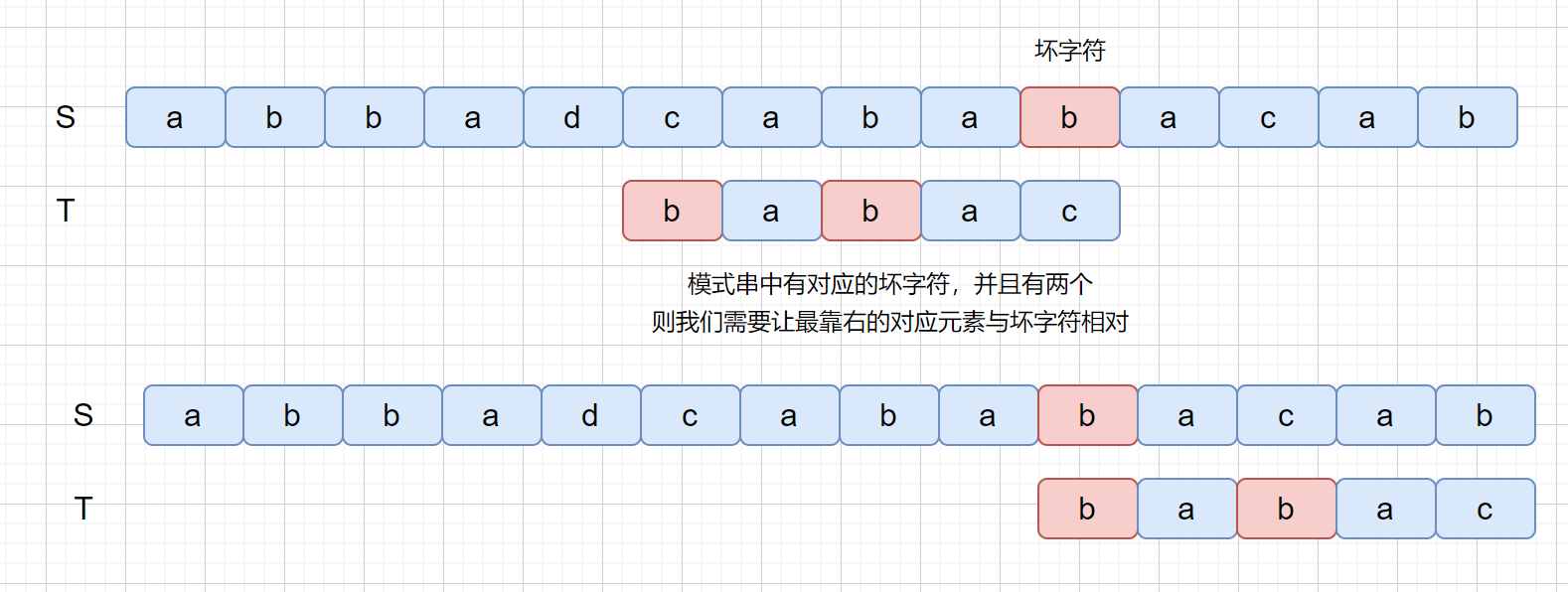
那么我们为什么要让**最靠右的对应元素与坏字符匹配**呢?如果上面的例子我们没有按照这条规则看下会产生什么问题。
|
||||
|
||||
|
||||
|
||||
如果没有按照我们上述规则,则会**漏掉我们的真正匹配**。我们的主串中是**含有 babac** 的,但是却**没有匹配成功**,所以应该遵守**最靠右的对应字符与坏字符相对**的规则。
|
||||
|
||||
我们上面一共介绍了三种移动情况,分别是下方的模式串中没有发现与坏字符对应的字符,发现一个对应字符,发现两个。这三种情况我们分别移动不同的位数,那我们是根据依据什么来决定移动位数的呢?下面我们给图中的字符加上下标。见下图
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
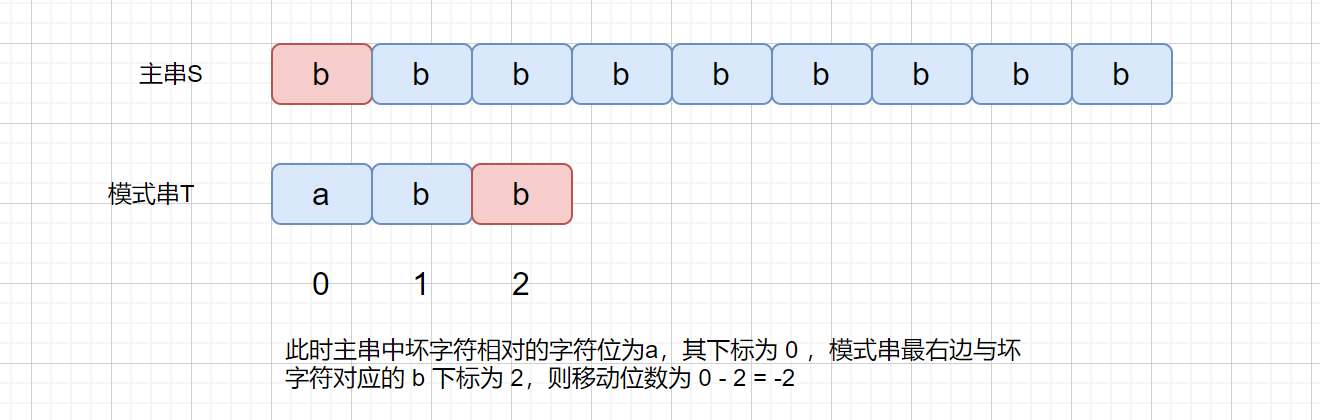
下面我们来考虑一下这种情况。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
此时这种情况肯定是不行的,不往右移动,甚至还有可能左移,那么我们有没有什么办法解决这个问题呢?继续往下看吧。
|
||||
|
||||
### 好后缀规则
|
||||
|
||||
好后缀其实也很容易理解,我们之前说过 BM 算法是从右往左进行比较,下面我们来看下面这个例子。
|
||||
|
||||

|
||||
|
||||
这里如果我们按照坏字符进行移动是不合理的,这时我们可以使用好后缀规则,那么什么是好后缀呢?
|
||||
|
||||
BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已经匹配成功,在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀,此时我们拿它在模式串中查找,如果找到了另一个和好后缀相匹配的串,那我们就将另一个和**好后缀相匹配**的串 ,滑到和好后缀对齐的位置。
|
||||
|
||||
是不是感觉有点拗口,没关系,我们看下图,红色代表坏字符,绿色代表好后缀
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
上面那种情况搞懂了,但是我们思考一下下面这种情况
|
||||
|
||||
|
||||
|
||||
上面我们说到了,如果在模式串的**头部**没有发现好后缀,发现好后缀的子串也可以。但是为什么要强调这个头部呢?
|
||||
|
||||
我们下面来看一下这种情况
|
||||
|
||||
|
||||
|
||||
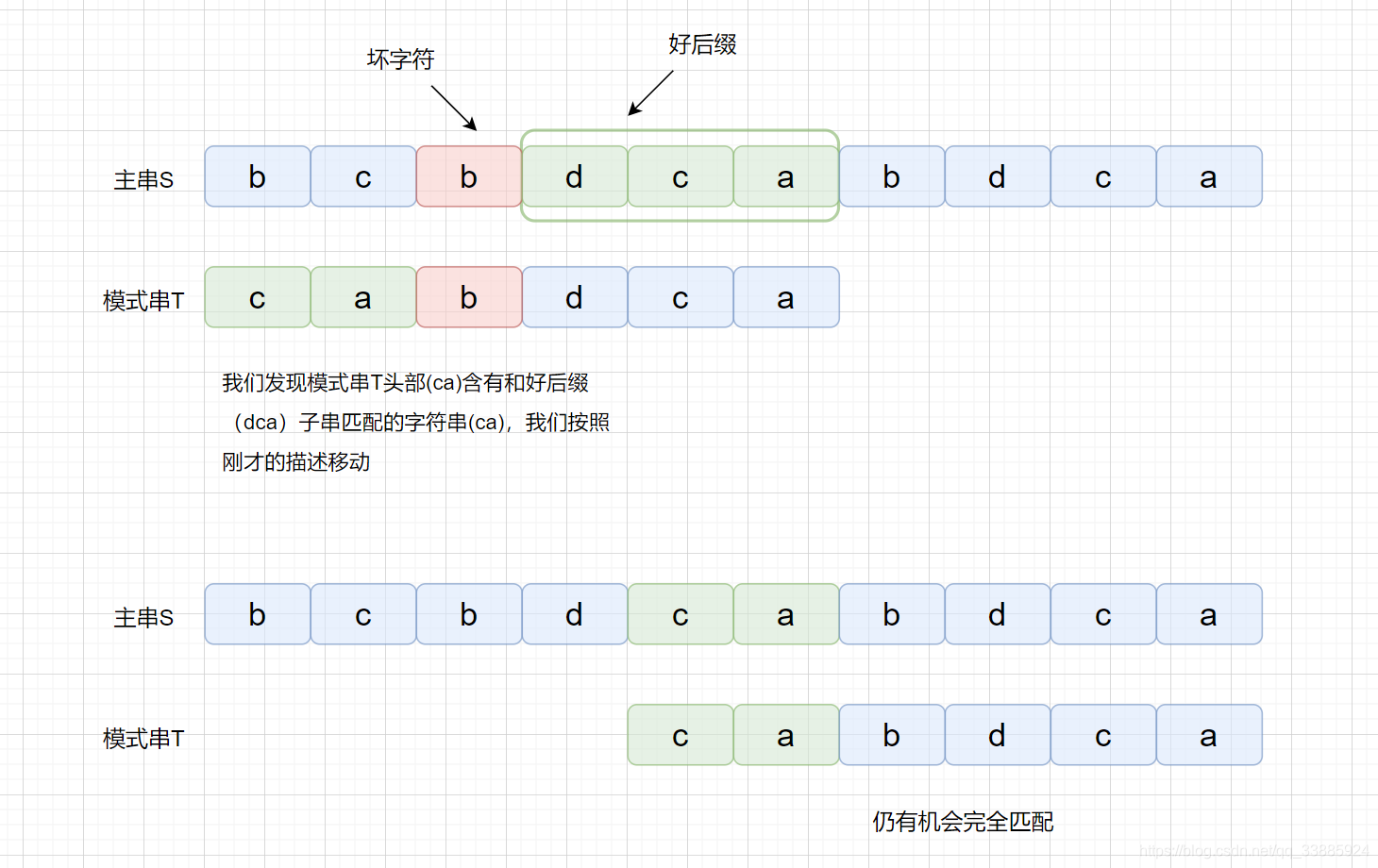
但是当我们在头部发现好后缀的子串时,是什么情况呢?
|
||||
|
||||
|
||||
|
||||
下面我们通过动图来看一下某一例子的具体的执行过程
|
||||
|
||||

|
||||
|
||||
说到这里,坏字符和好后缀规则就算说完了,坏字符很容易理解,我们对好后缀总结一下
|
||||
|
||||
1.如果模式串**含有好后缀**,无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次,则以**最右侧的好后缀**为基准。
|
||||
|
||||
2.如果模式串**头部含有**好后缀子串则可以按照规则进行移动,中间部分含有好后缀子串则不可以。
|
||||
|
||||
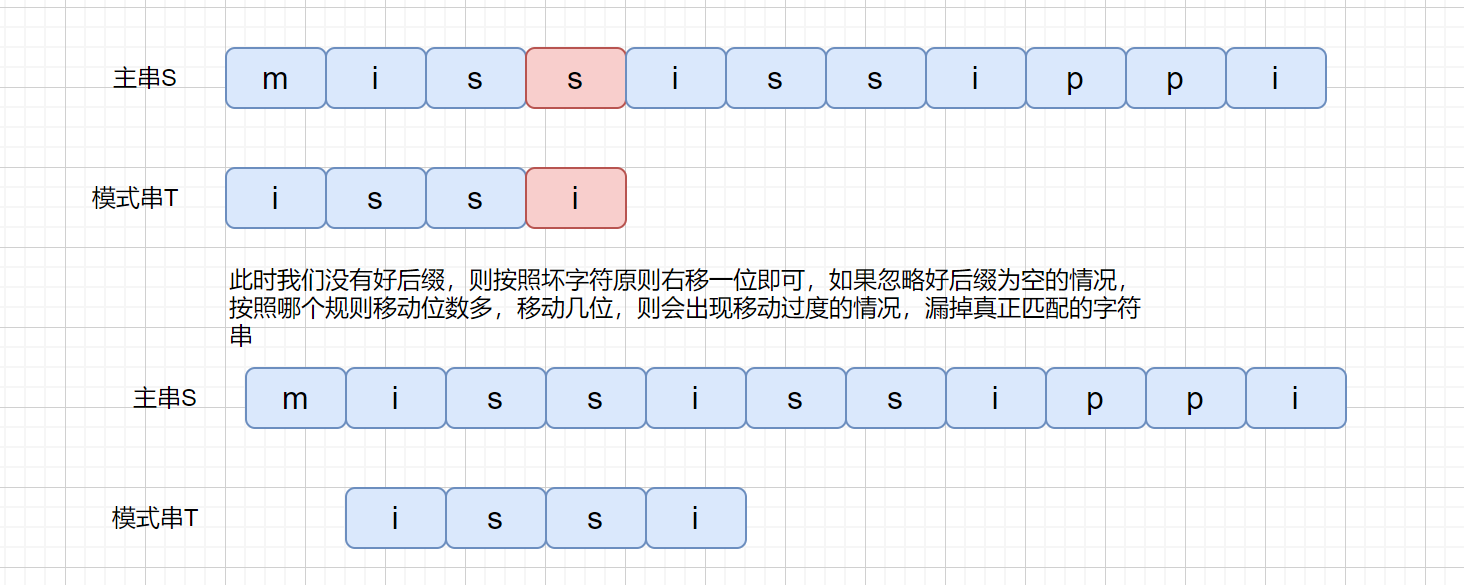
3.如果在模式串尾部就出现不匹配的情况,即不存在好后缀时,则根据坏字符进行移动,这里有的文章没有提到,是个需要特别注意的地方,我是在这个论文里找到答案的,感兴趣的同学可以看下。
|
||||
|
||||
> Boyer R S,Moore J S. A fast string searching algorithm[J]. Communications of the ACM,1977,10: 762-772.
|
||||
|
||||
|
||||
|
||||
之前我们刚开始说坏字符的时候,是不是有可能会出现负值的情况,即往左移动的情况,所以我们为了解决这个问题,我们可以分别计算好后缀和坏字符往后滑动的位数**(好后缀不为 0 的情况)**,然后取两个数中最大的,作为模式串往后滑动的位数。
|
||||
|
||||
|
||||
|
||||
这破图画起来是真费劲啊。下面我们来看一下算法代码,代码有点长,我都标上了注释也在网站上 AC 了,如果各位感兴趣可以看一下,不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
char[] hay = haystack.toCharArray();
|
||||
char[] need = needle.toCharArray();
|
||||
int haylen = haystack.length();
|
||||
int needlen = need.length;
|
||||
return bm(hay,haylen,need,needlen);
|
||||
}
|
||||
//用来求坏字符情况下移动位数
|
||||
private static void badChar(char[] b, int m, int[] bc) {
|
||||
//初始化
|
||||
for (int i = 0; i < 256; ++i) {
|
||||
bc[i] = -1;
|
||||
}
|
||||
//m 代表模式串的长度,如果有两个 a,则后面那个会覆盖前面那个
|
||||
for (int i = 0; i < m; ++i) {
|
||||
int ascii = (int)b[i];
|
||||
bc[ascii] = i;//下标
|
||||
}
|
||||
}
|
||||
//用来求好后缀条件下的移动位数
|
||||
private static void goodSuffix (char[] b, int m, int[] suffix,boolean[] prefix) {
|
||||
//初始化
|
||||
for (int i = 0; i < m; ++i) {
|
||||
suffix[i] = -1;
|
||||
prefix[i] = false;
|
||||
}
|
||||
for (int i = 0; i < m - 1; ++i) {
|
||||
int j = i;
|
||||
int k = 0;
|
||||
while (j >= 0 && b[j] == b[m-1-k]) {
|
||||
--j;
|
||||
++k;
|
||||
suffix[k] = j + 1;
|
||||
}
|
||||
if (j == -1) prefix[k] = true;
|
||||
}
|
||||
}
|
||||
public static int bm (char[] a, int n, char[] b, int m) {
|
||||
|
||||
int[] bc = new int[256];//创建一个数组用来保存最右边字符的下标
|
||||
badChar(b,m,bc);
|
||||
//用来保存各种长度好后缀的最右位置的数组
|
||||
int[] suffix_index = new int[m];
|
||||
//判断是否是头部,如果是头部则true
|
||||
boolean[] ispre = new boolean[m];
|
||||
goodSuffix(b,m,suffix_index,ispre);
|
||||
int i = 0;//第一个匹配字符
|
||||
//注意结束条件
|
||||
while (i <= n-m) {
|
||||
int j;
|
||||
//从后往前匹配,匹配失败,找到坏字符
|
||||
for (j = m - 1; j >= 0; --j) {
|
||||
if (a[i+j] != b[j]) break;
|
||||
}
|
||||
//模式串遍历完毕,匹配成功
|
||||
if (j < 0) {
|
||||
return i;
|
||||
}
|
||||
//下面为匹配失败时,如何处理
|
||||
//求出坏字符规则下移动的位数,就是我们坏字符下标减最右边的下标
|
||||
int x = j - bc[(int)a[i+j]];
|
||||
int y = 0;
|
||||
//好后缀情况,求出好后缀情况下的移动位数,如果不含有好后缀的话,则按照坏字符来
|
||||
if (y < m-1 && m - 1 - j > 0) {
|
||||
y = move(j, m, suffix_index,ispre);
|
||||
}
|
||||
//移动
|
||||
i = i + Math.max(x,y);
|
||||
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
// j代表坏字符的下标
|
||||
private static int move (int j, int m, int[] suffix_index, boolean[] ispre) {
|
||||
//好后缀长度
|
||||
int k = m - 1 - j;
|
||||
//如果含有长度为 k 的好后缀,返回移动位数,
|
||||
if (suffix_index[k] != -1) return j - suffix_index[k] + 1;
|
||||
//找头部为好后缀子串的最大长度,从长度最大的子串开始
|
||||
for (int r = j + 2; r <= m-1; ++r) {
|
||||
//如果是头部
|
||||
if (ispre[m-r] == true) {
|
||||
return r;
|
||||
}
|
||||
}
|
||||
//如果没有发现好后缀匹配的串,或者头部为好后缀子串,则移动到 m 位,也就是匹配串的长度
|
||||
return m;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
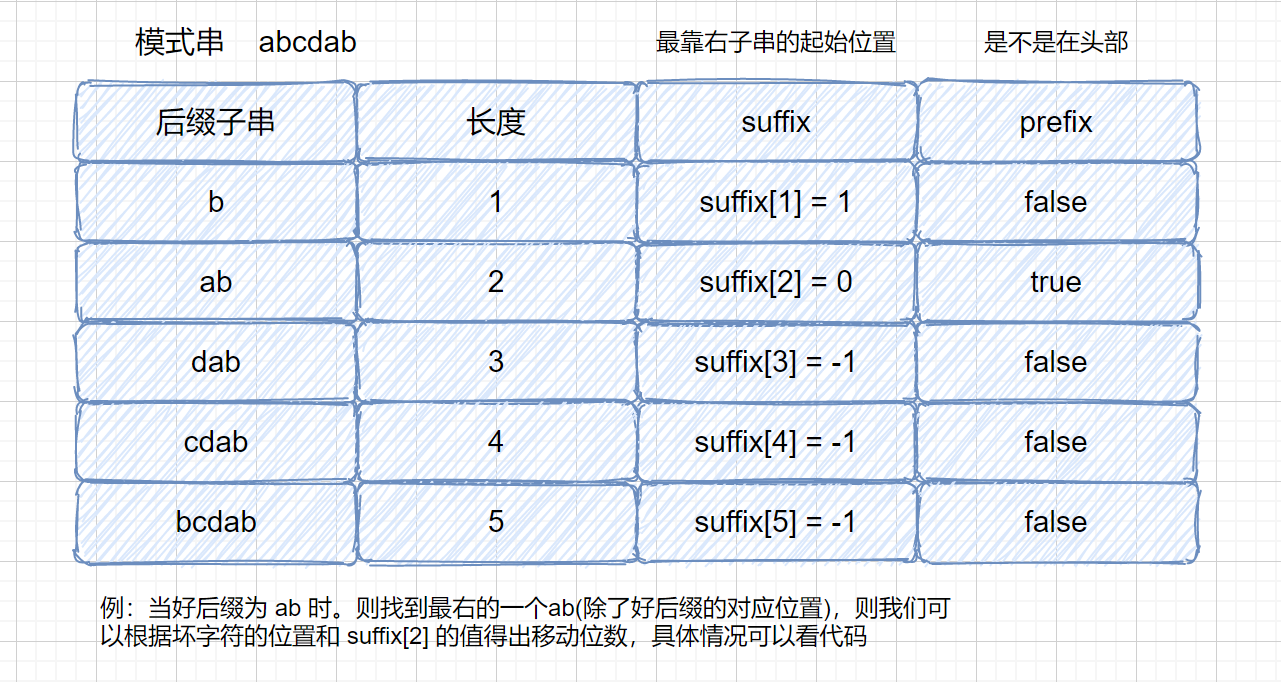
我们来理解一下我们代码中用到的两个数组,因为两个规则的移动位数,只与模式串有关,与主串无关,所以我们可以提前求出每种情况的移动情况,保存到数组中。
|
||||
|
||||
|
||||
363
gif-algorithm/数据结构和算法/Hash表的那些事.md
Normal file
363
gif-algorithm/数据结构和算法/Hash表的那些事.md
Normal file
@@ -0,0 +1,363 @@
|
||||
# 散列(哈希)表总结
|
||||
|
||||
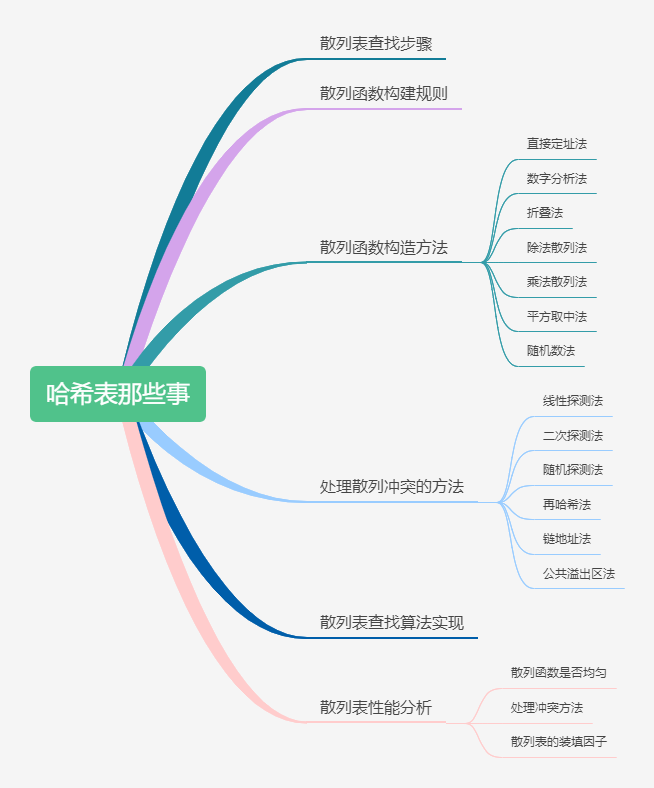
之前给大家介绍了**链表**,**栈和队列**今天我们来说一种新的数据结构散列(哈希)表,散列是应用非常广泛的数据结构,在我们的刷题过程中,散列表的出场率特别高。所以我们快来一起把散列表的内些事给整明白吧。文章框架如下
|
||||
|
||||
|
||||
|
||||
说散列表之前,我们先设想以下场景。
|
||||
|
||||
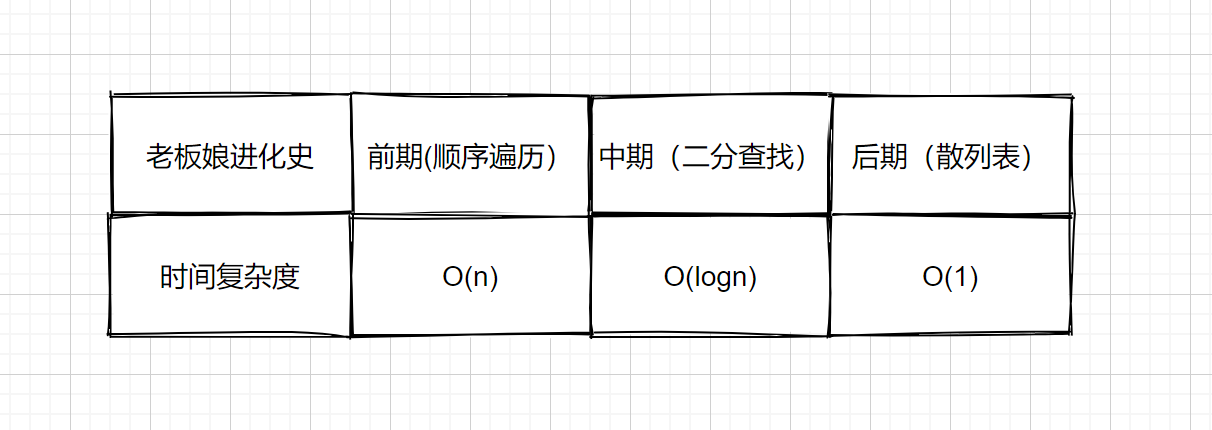
> 袁厨穿越回了古代,凭借从现代学习的做饭手艺,开了一个袁记菜馆,正值开业初期,店里生意十分火爆,但是顾客结账时就犯难了,每当结账的时候,老板娘总是按照菜单一个一个找价格(遍历查找),每次都要找半天,所以结账的地方总是排起长队,顾客们表示用户体验不咋滴。袁厨一想这不是办法啊,让顾客老是等着,太影响客户体验啦。所以袁厨就先把菜单按照首字母排序(二分查找),然后查找的时候根据首字母查找,这样结账的时候就能大大提高检索效率啦!但是呢?工作日顾客不多,老板娘完全应付的过来,但是每逢节假日,还是会排起长队。那么有没有什么更好的办法呢?对呀!我们把所有的价格都背下来不就可以了吗?每个菜的价格我们都了如指掌,结账的时候我们只需简单相加即可。所以袁厨和老板娘加班加点的进行背诵。下次再结账的时候一说吃了什么菜,我们立马就知道价格啦。自此以后收银台再也没有出现过长队啦,袁记菜馆开着开着一不小心就成了天下第一饭店了。
|
||||
|
||||
下面我们来看一下袁记菜馆老板娘进化史。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
上面的后期结账的过程则模拟了我们的散列表查找,那么在计算机中是如何使用进行查找的呢?
|
||||
|
||||
### 散列表查找步骤
|
||||
|
||||
散列表-------最有用的基本数据结构之一。是根据关键码的值儿直接进行访问的数据结构,散列表的实现常常叫做**散列(hasing)**。散列是一种用于以**常数平均时间**执行插入、删除和查找的技术,下面我们来看一下散列过程。
|
||||
|
||||
我们的整个散列过程主要分为两步
|
||||
|
||||
(1)通过**散列函数**计算记录的散列地址,并按此**散列地址**存储该记录。就好比麻辣鱼我们就让它在川菜区,糖醋鱼,我们就让它在鲁菜区。但是我们需要注意的是,无论什么记录我们都需要用**同一个散列函数**计算地址,再存储。
|
||||
|
||||
(2)当我们查找时,我们通过**同样的散列函数**计算记录的散列地址,按此散列地址访问该记录。因为我们存和取得时候用的都是一个散列函数,因此结果肯定相同。
|
||||
|
||||
刚才我们在散列过程中提到了散列函数,那么散列函数是什么呢?
|
||||
|
||||
我们假设某个函数为 **f**,使得
|
||||
|
||||
**存储位置 = f (关键字)**
|
||||
|
||||
**输入:关键字** **输出:存储位置(散列地址)**
|
||||
|
||||
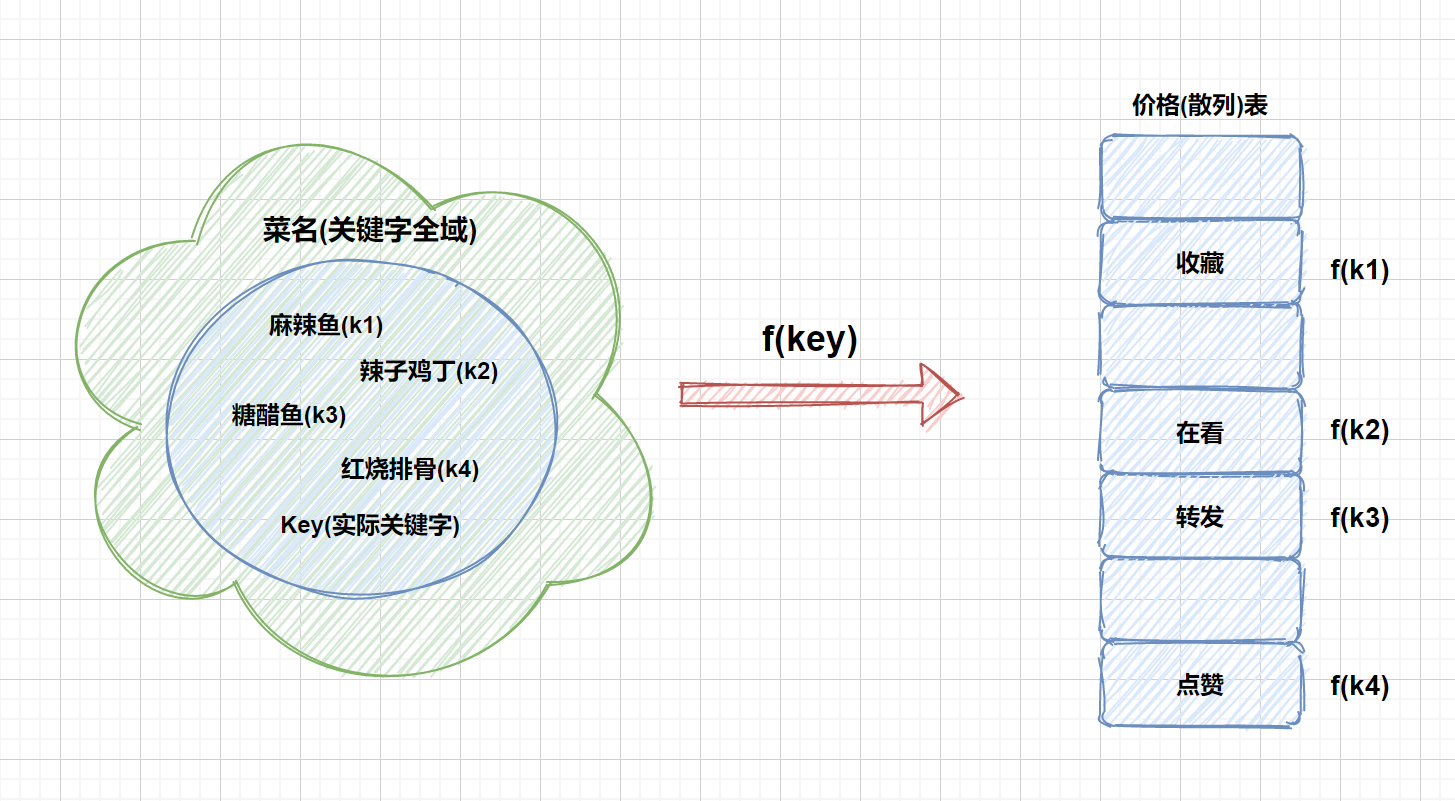
那样我们就能通过查找关键字**不需要比较**就可获得需要的记录的存储位置。这种存储技术被称为散列技术。散列技术是在通过记录的存储位置和它的关键字之间建立一个确定的对应关系 **f** ,使得每个关键字 **key** 都对应一个存储位置 **f(key)**。见下图
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
这里的 **f** 就是我们所说的散列函数(哈希)函数。我们利用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间就是我们本文的主人公------**散列(哈希)表**
|
||||
|
||||
上图为我们描述了用散列函数将关键字映射到散列表,但是大家有没有考虑到这种情况,那就是将关键字映射到同一个槽中的情况,即 **f(k4) = f(k3)** 时。这种情况我们将其称之为**冲突**,**k3** 和 **k4**则被称之为散列函数 **f** 的**同义词**,如果产生这种情况,则会让我们查找错误。幸运的是我们能找到有效的方法解决冲突。
|
||||
|
||||
首先我们可以对哈希函数下手,我们可以精心设计哈希函数,让其尽可能少的产生冲突,所以我们创建哈希函数时应遵循以下规则
|
||||
|
||||
(1)**必须是一致的**,假设你输入辣子鸡丁时得到的是**在看**,那么每次输入辣子鸡丁时,得到的也必须为**在看**。如果不是这样,散列表将毫无用处。
|
||||
|
||||
(2)**计算简单**,假设我们设计了一个算法,可以保证所有关键字都不会冲突,但是这个算法计算复杂,会耗费很多时间,这样的话就大大降低了查找效率,反而得不偿失。所以咱们**散列函数的计算时间不应该超过其他查找技术与关键字的比较时间**,不然的话我们干嘛不使用其他查找技术呢?
|
||||
|
||||
(3)**散列地址分布均匀**我们刚才说了冲突的带来的问题,所以我们最好的办法就是让**散列地址尽量均匀分布在存储空间中**,这样即保证空间的有效利用,又减少了处理冲突而消耗的时间。
|
||||
|
||||
现在我们已经对散列表,散列函数等知识有所了解啦,那么我们来看几种常用的散列函数构造规则。这些方法的共同点为都是将原来的数字按某种规律变成了另一个数字。
|
||||
|
||||
### 散列函数构造方法
|
||||
|
||||
#### 直接定址法
|
||||
|
||||
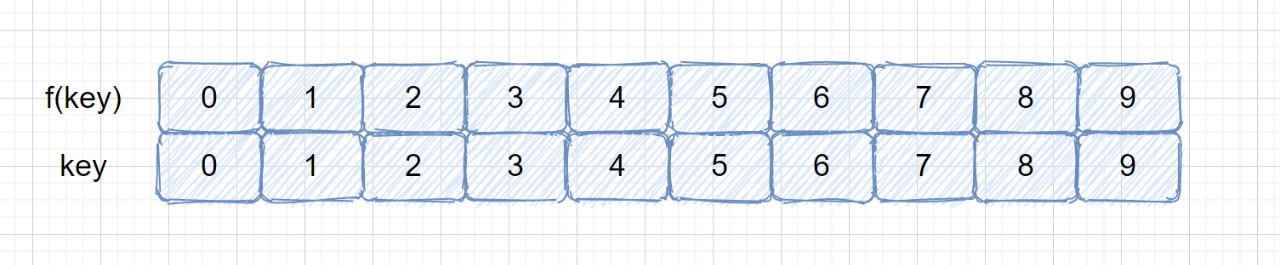
如果我们对盈利为0-9的菜品设计哈希表,我们则直接可以根据作为地址,则 **f(key) = key**;
|
||||
|
||||
即下面这种情况。
|
||||
|
||||
|
||||
|
||||
有没有感觉上面的图很熟悉,没错我们经常用的数组其实就是一张哈希表,关键码就是数组的索引下标,然后我们通过下标直接访问数组中的元素。
|
||||
|
||||
另外我们假设每道菜的成本为50块,那我们还可以根据盈利+成本来作为地址,那么则 f(key) = key + 50。也就是说我们可以根据线性函数值作为散列地址。
|
||||
|
||||
**f(key) = a * key + b** **a,b均为常数**
|
||||
|
||||
优点:简单、均匀、无冲突。
|
||||
|
||||
应用场景:需要事先知道关键字的分布情况,适合查找表较小且连续的情况
|
||||
|
||||
#### 数字分析法
|
||||
|
||||
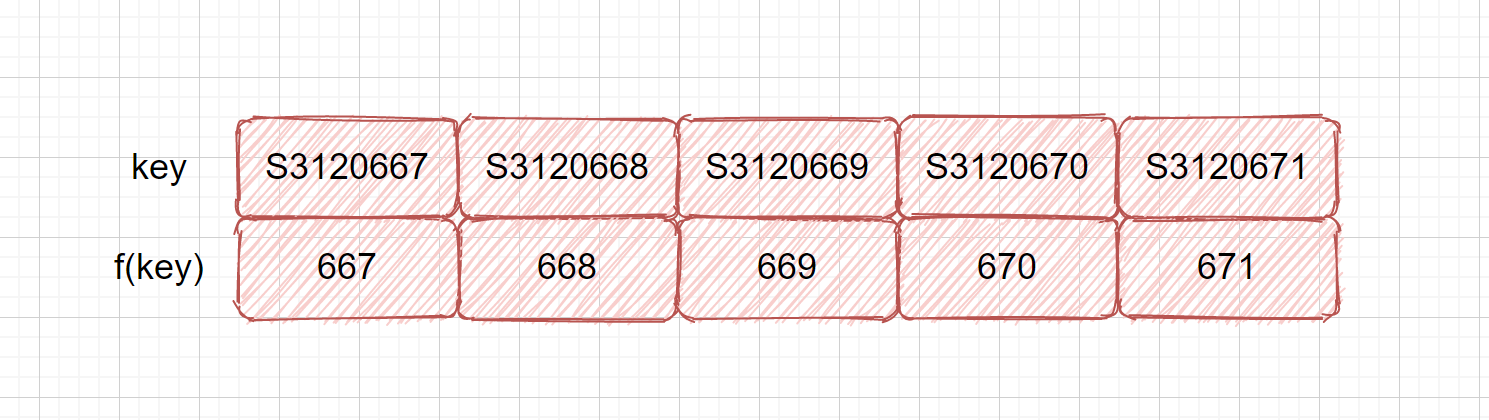
该方法也是十分简单的方法,就是分析我们的关键字,取其中一段,或对其位移,叠加,用作地址。比如我们的学号,前 6 位都是一样的,但是后面 3 位都不相同,我们则可以用学号作为键,后面的 3 位做为我们的散列地址。如果我们这样还是容易产生冲突,则可以对抽取数字再进行处理。我们的目的只有一个,提供一个散列函数将关键字合理的分配到散列表的各位置。这里我们提到了一种新的方式,抽取,这也是在散列函数中经常用到的手段。
|
||||
|
||||
|
||||
|
||||
优点:简单、均匀、适用于关键字位数较大的情况
|
||||
|
||||
应用场景:关键字位数较大,知道关键字分布情况且关键字的若干位较均匀
|
||||
|
||||
#### 折叠法
|
||||
|
||||
其实这个方法也很简单,也是处理我们的关键字然后用作我们的散列地址,主要思路是将关键字从左到右分割成位数相等的几部分,然后叠加求和,并按散列表表长,取后几位作为散列地址。
|
||||
|
||||
比如我们的关键字是123456789,则我们分为三部分 123 ,456 ,789 然后将其相加得 1368 然后我们再取其后三位 368 作为我们的散列地址。
|
||||
|
||||
优点:事先不需要知道关键字情况
|
||||
|
||||
应用场景:适合关键字位数较多的情况
|
||||
|
||||
#### 除法散列法
|
||||
|
||||
在用来设计散列函数的除法散列法中,通过取 key 除以 p 的余数,将关键字映射到 p 个槽中的某一个上,对于散列表长度为 m 的散列函数公式为
|
||||
|
||||
**f(k) = k mod p (p <= m)**
|
||||
|
||||
例如,如果散列表长度为 12,即 m = 12 ,我们的参数 p 也设为12,**那 k = 100时 f(k) = 100 % 12 = 4**
|
||||
|
||||
由于只需要做一次除法操作,所以除法散列法是非常快的。
|
||||
|
||||
由上面的公式可以看出,该方法的重点在于 p 的取值,如果 p 值选的不好,就可能会容易产生同义词。见下面这种情况。我们哈希表长度为6,我们选择6为p值,则有可能产生这种情况,所有关键字都得到了0这个地址数。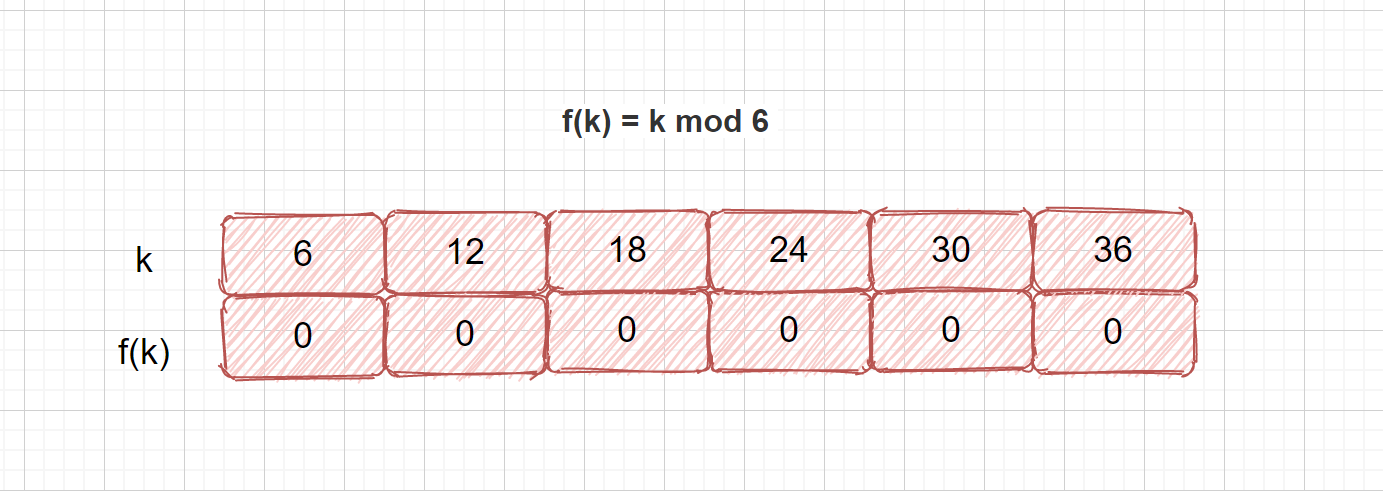
|
||||
|
||||
那我们在选用除法散列法时选取 p 值时应该遵循怎样的规则呢?
|
||||
|
||||
- m 不应为 2 的幂,因为如果 m = 2^p ,则 f(k) 就是 k 的 p 个最低位数字。例 12 % 8 = 4 ,12的二进制表示位1100,后三位为100。
|
||||
- 若散列表长为 m ,通常 p 为 小于或等于表长(最好接近m)的最小质数或不包含小于 20 质因子的合数。
|
||||
|
||||
> **合数:**合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。
|
||||
>
|
||||
> **质因子**:质因子(或质因数)在数论里是指能整除给定正整数的质数。
|
||||
|
||||
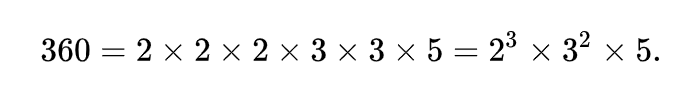
|
||||
|
||||
这里的2,3,5为质因子
|
||||
|
||||
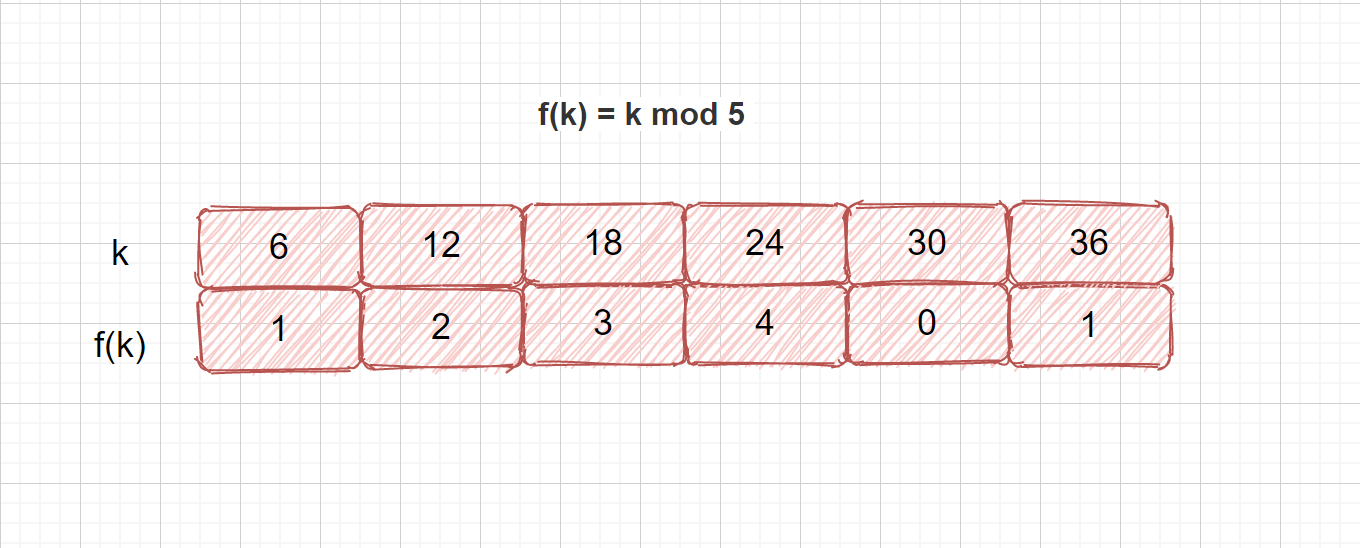
还是上面的例子,我们根据规则选择 5 为 p 值,我们再来看。这时我们发现只有 6 和 36 冲突,相对来说就好了很多。
|
||||
|
||||
|
||||
|
||||
优点:计算效率高,灵活
|
||||
|
||||
应用场景:不知道关键字分布情况
|
||||
|
||||
#### 乘法散列法
|
||||
|
||||
构造散列函数的乘法散列法主要包含两个步骤
|
||||
|
||||
- 用关键字 k 乘上常数 A(0 < A < 1),并提取 k A 的小数部分
|
||||
- 用 m 乘以这个值,再向下取整
|
||||
|
||||
散列函数为
|
||||
|
||||
**f (k) = ⌊ m(kA mod 1) ⌋**
|
||||
|
||||
这里的 **kA mod 1** 的含义是取 keyA 的小数部分,即 **kA - ⌊kA⌋** 。
|
||||
|
||||
优点:对 m 的选择不是特别关键,一般选择它为 2 的某个幂次(m = 2 ^ p ,p为某个整数)
|
||||
|
||||
应用场景:不知道关键字情况
|
||||
|
||||
#### 平方取中法
|
||||
|
||||
这个方法就比较简单了,假设关键字是 321,那么他的平方就是 103041,再抽取中间的 3 位就是 030 或 304 用作散列地址。再比如关键字是 1234 那么它的平方就是 1522756 ,抽取中间 3 位就是 227 用作散列地址.
|
||||
|
||||
优点:灵活,适用范围广泛
|
||||
|
||||
适用场景:不知道关键字分布,而位数又不是很大的情况。
|
||||
|
||||
#### 随机数法
|
||||
|
||||
故名思意,取关键字的随机函数值为它的散列地址。也就是 **f(key) = random(key)**。这里的random是 随机函数。
|
||||
|
||||
优点:易实现
|
||||
|
||||
适用场景:关键字的长度不等时
|
||||
|
||||
上面我们的例子都是通过数字进行举例,那么如果是字符串可不可以作为键呢?当然也是可以的,各种各样的符号我们都可以转换成某种数字来对待,比如我们经常接触的ASCII 码,所以是同样适用的。
|
||||
|
||||
以上就是常用的散列函数构造方法,其实他们的中心思想是一致的,将关键字经过加工处理之后变成另外一个数字,而这个数字就是我们的存储位置,是不是有一种间谍传递情报的感觉。
|
||||
|
||||
一个好的哈希函数可以帮助我们尽可能少的产生冲突,但是也不能完全避免产生冲突,那么遇到冲突时应该怎么做呢?下面给大家带来几种常用的处理散列冲突的方法。
|
||||
|
||||
### 处理散列冲突的方法
|
||||
|
||||
我们在使用 hash 函数之后发现关键字 key1 不等于 key2 ,但是 f(key1) = f(key2),即有冲突,那么该怎么办呢?不急我们慢慢往下看。
|
||||
|
||||
#### 开放地址法
|
||||
|
||||
了解开放地址法之前我们先设想以下场景。
|
||||
|
||||
> 袁记菜馆内,铃铃铃,铃铃铃 电话铃响了
|
||||
>
|
||||
> 大鹏:老袁,给我订个包间,我今天要去带几个客户去你那谈生意。
|
||||
>
|
||||
> 袁厨:大鹏啊,你常用的那个包间被人订走啦。
|
||||
>
|
||||
> 大鹏:老袁你这不仗义呀,咋没给我留住呀,那你给我找个**空房间**吧。
|
||||
>
|
||||
> 袁厨:好滴老哥
|
||||
|
||||
哦,穿越回古代就没有电话啦,那看来穿越的时候得带着几个手机了。
|
||||
|
||||
上面的场景其实就是一种处理冲突的方法-----开放地址法
|
||||
|
||||
**开放地址法**就是一旦发生冲突,就去寻找下一个空的散列地址,只要列表足够大,空的散列地址总能找到,并将记录存入,为了使用开放寻址法插入一个元素,需要连续地检查散列表,或称为**探查**,我们常用的有**线性探测,二次探测,随机探测**。
|
||||
|
||||
##### 线性探测法
|
||||
|
||||
下面我们先来看一下线性探测,公式:
|
||||
|
||||
> **f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
||||
|
||||
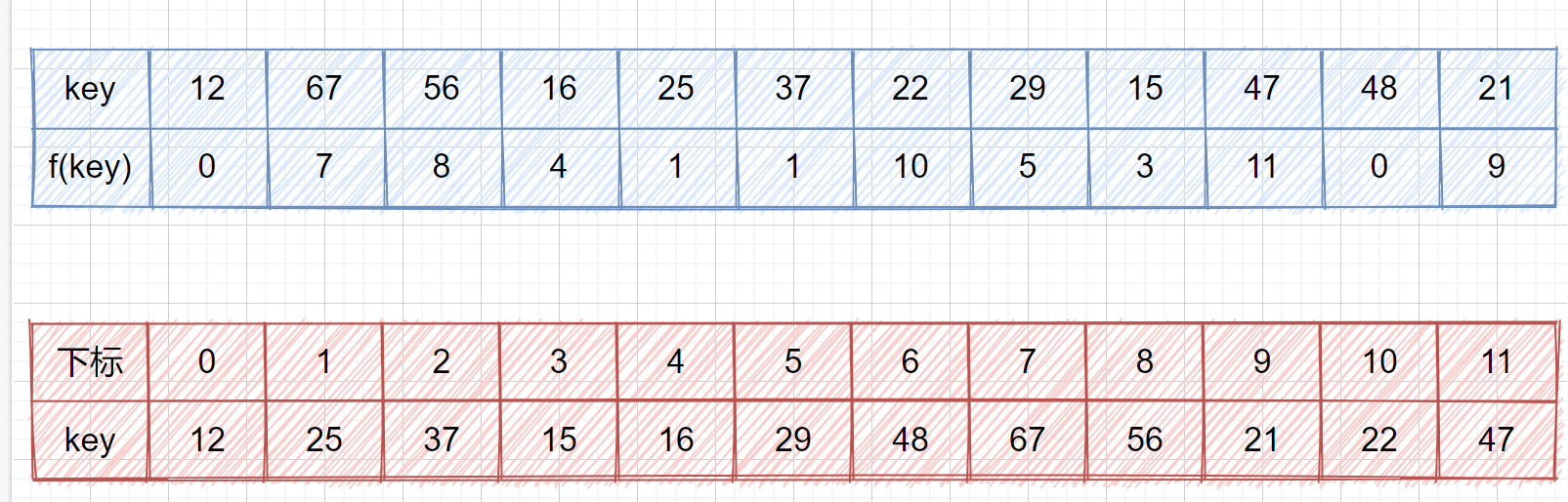
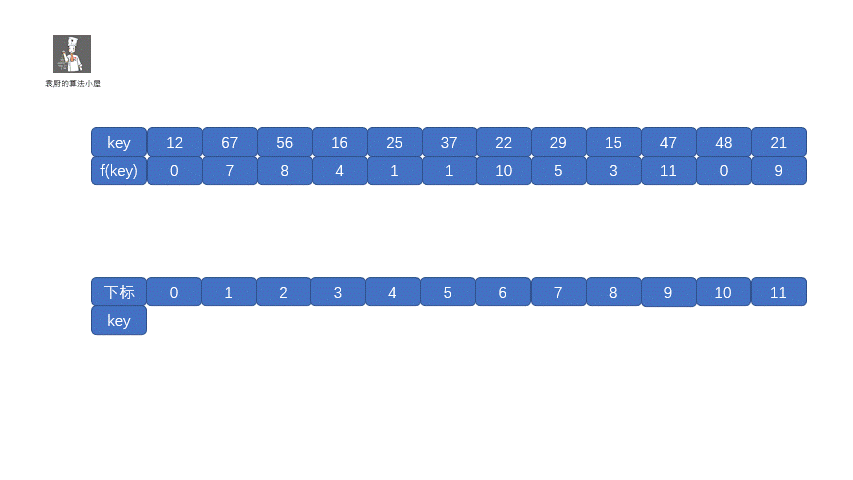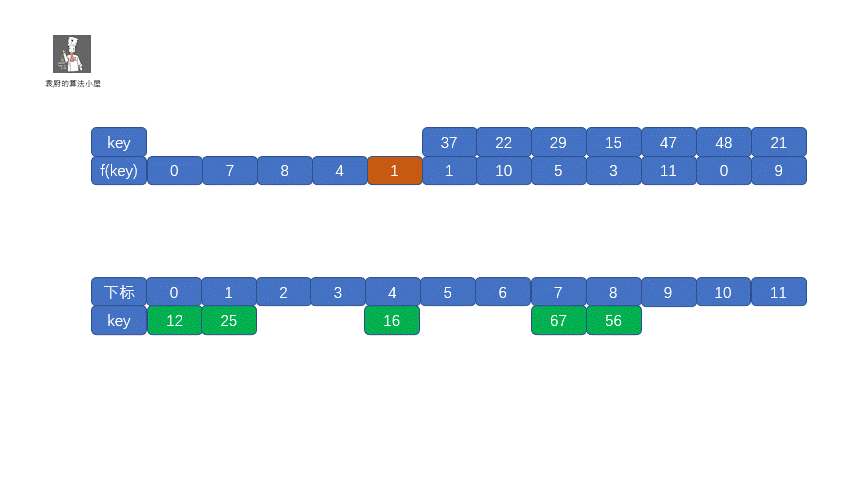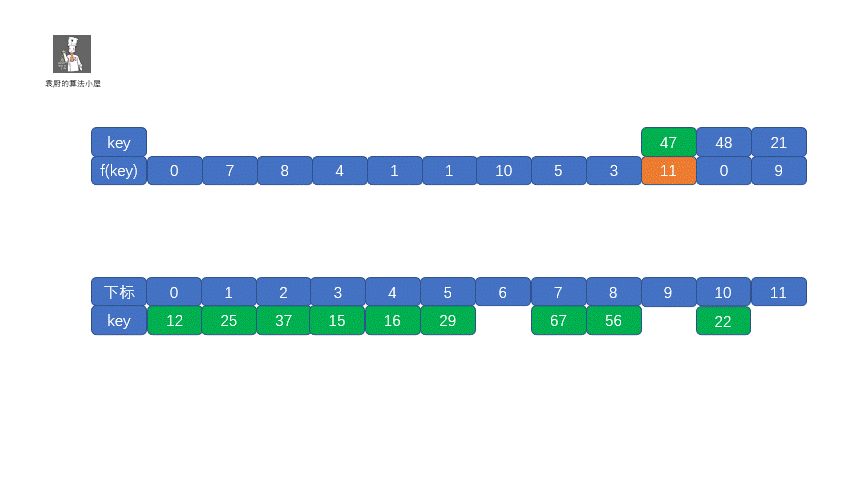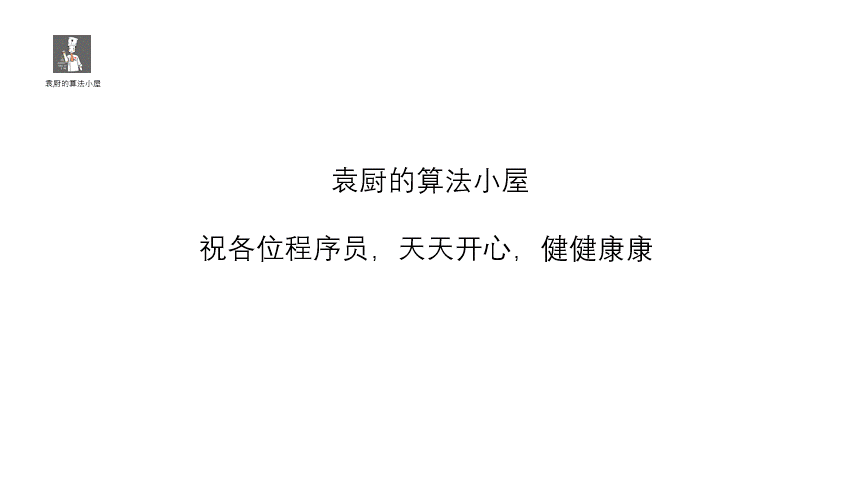
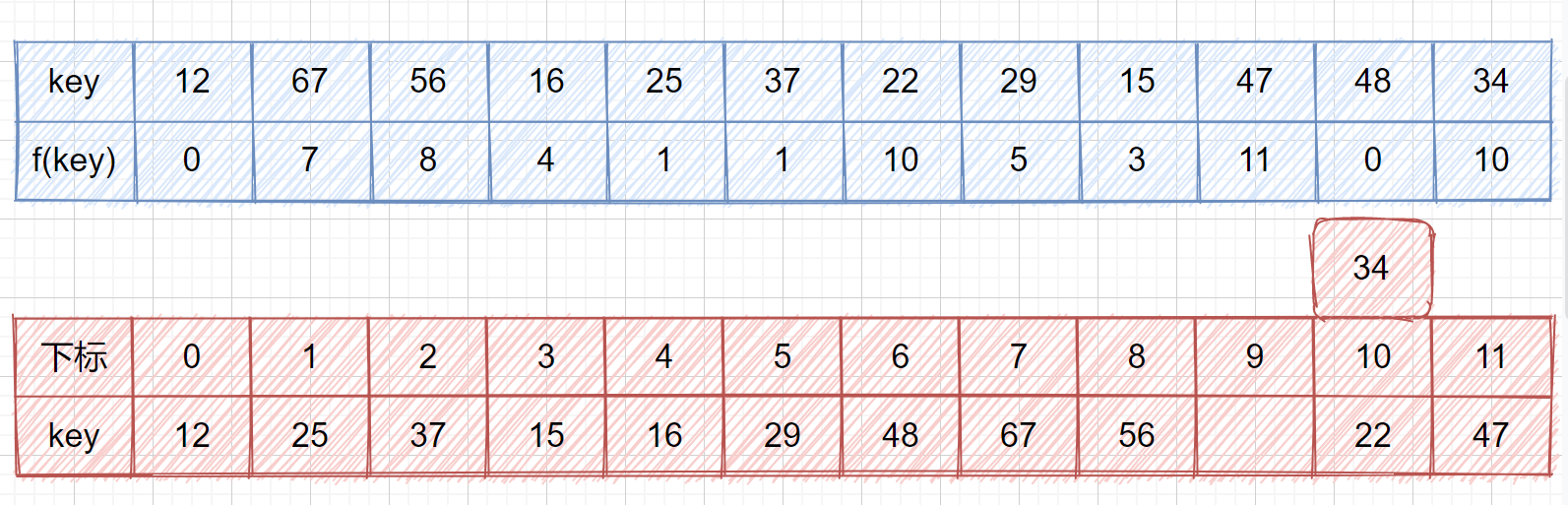
我们来看一个例子,我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为12,我们再用散列函数 **f(key) = key mod 12。**
|
||||
|
||||
我们求出每个 key 的 f(key)见下表
|
||||
|
||||

|
||||
|
||||
我们查看上表发现,前五位的 **f(key)** 都不相同,即没有冲突,可以直接存入,但是到了第六位 **f(37) = f(25) = 1**,那我们就需要利用上面的公式 **f(37) = f (f(37) + 1 ) mod 12 = 2**,这其实就是我们的订包间的做法。下面我们看一下将上面的所有数存入哈希表是什么情况吧。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
我们把这种解决冲突的开放地址法称为**线性探测法**。下面我们通过视频来模拟一下线性探测法的存储过程。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
另外我们在解决冲突的时候,会遇到 48 和 37 虽然不是同义词,却争夺一个地址的情况,我们称其为**堆积**。因为堆积使得我们需要不断的处理冲突,插入和查找效率都会大大降低。
|
||||
|
||||
通过上面的视频我们应该了解了线性探测的执行过程了,那么我们考虑一下这种情况,若是我们的最后一位不为21,为 34 时会有什么事情发生呢?
|
||||
|
||||
|
||||
|
||||
此时他第一次会落在下标为 10 的位置,那么如果继续使用线性探测的话,则需要通过不断取余后得到结果,数据量小还好,要是很大的话那也太慢了吧,但是明明他的前面就有一个空房间呀,如果向前移动只需移动一次即可。不要着急,前辈们已经帮我们想好了解决方法
|
||||
|
||||
##### 二次探测法
|
||||
|
||||
其实理解了我们的上个例子之后,这个一下就能整明白了,根本不用费脑子,这个方法就是更改了一下di的取值
|
||||
|
||||
> **线性探测: f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
||||
>
|
||||
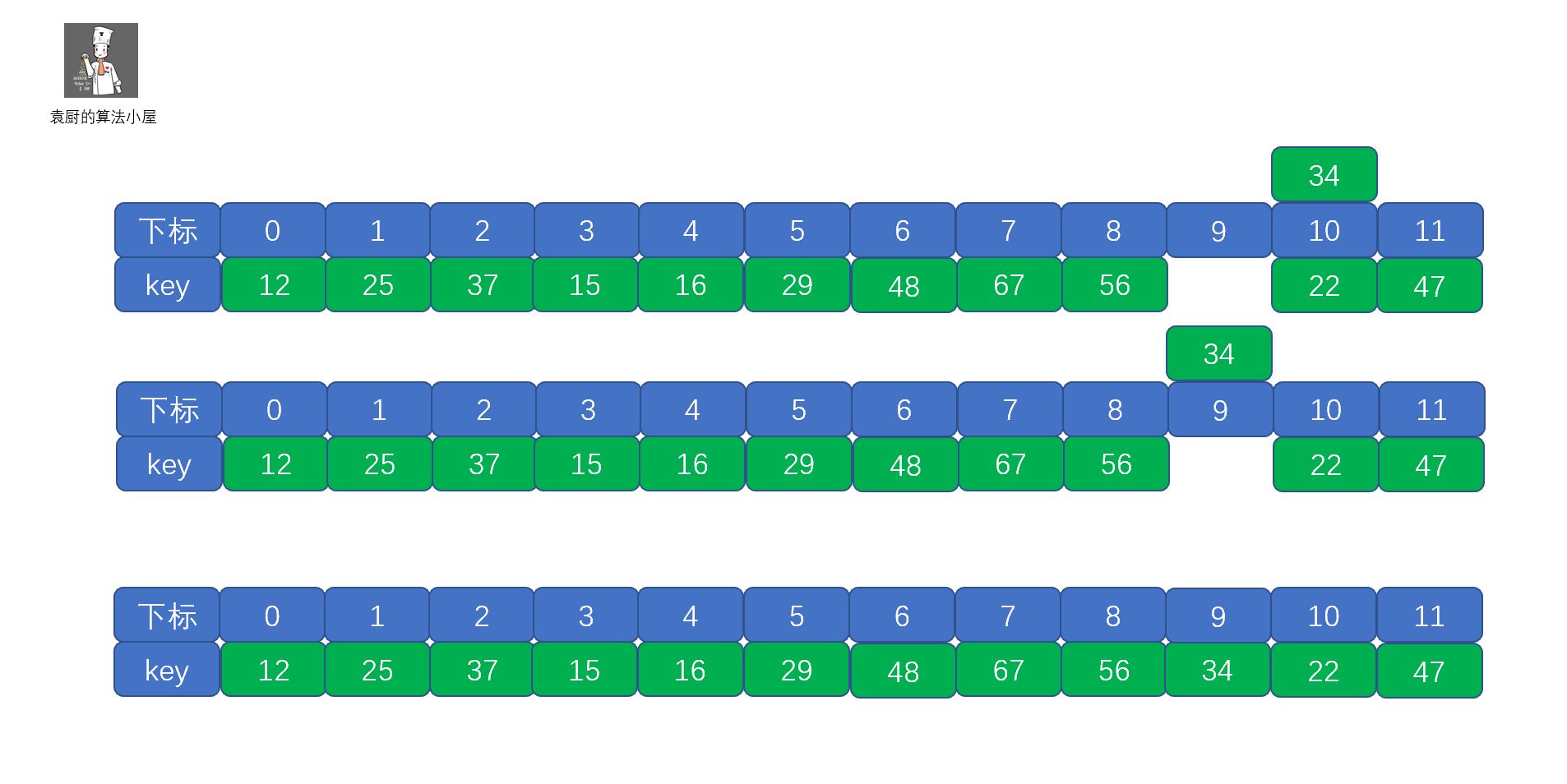
> **二次探测:** **f,(key) = ( f(key) + di ) MOD m(di =1^2 , -1^2 , 2^2 , -2^2 .... q^2, -q^2, q<=m/2)**
|
||||
|
||||
**注:这里的是 -1^2 为负值 而不是 (-1)^2**
|
||||
|
||||
所以对于我们的34来说,当di = -1时,就可以找到空位置了。
|
||||
|
||||
|
||||
|
||||
二次探测法的目的就是为了不让关键字聚集在某一块区域。另外还有一种有趣的方法,位移量采用随机函数计算得到,接着往下看吧.
|
||||
|
||||
##### 随机探测法
|
||||
|
||||
大家看到这是不又有新问题了,刚才我们在散列函数构造规则的第一条中说
|
||||
|
||||
> (1)**必须是一致的**,假设你输入辣子鸡丁时得到的是**在看**,那么每次输入辣子鸡丁时,得到的也必须为**在看**。如果不是这样,散列表将毫无用处。
|
||||
|
||||
咦?怎么又是**在看**哈哈,那么问题来了,我们使用随机数作为他的偏移量,那么我们查找的时候岂不是查不到了?因为我们 di 是随机生成的呀,这里的随机其实是伪随机数,伪随机数含义为,我们设置**随机种子**相同,则不断调用随机函数可以生成**不会重复的数列**,我们在查找时,**用同样的随机种子**,**它每次得到的数列是相同的**,那么相同的 di 就能得到**相同的散列地址**。
|
||||
|
||||
> 随机种子(Random Seed)是计算机专业术语,一种以随机数作为对象的以真随机数(种子)为初始条件的随机数。一般计算机的随机数都是伪随机数,以一个真随机数(种子)作为初始条件,然后用一定的算法不停迭代产生随机数
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
通过上面的测试是不是一下就秒懂啦,为什么我们可以使用随机数作为它的偏移量,理解那句,相同的随机种子,他每次得到的数列是相同的。
|
||||
|
||||
下面我们再来看一下其他的函数处理散列冲突的方法
|
||||
|
||||
#### 再哈希法
|
||||
|
||||
这个方法其实也特别简单,利用不同的哈希函数再求得一个哈希地址,直到不出现冲突为止。
|
||||
|
||||
> **f,(key) = RH,( key ) (i = 1,2,3,4.....k)**
|
||||
|
||||
这里的RH,就是不同的散列函数,你可以把我们之前说过的那些散列函数都用上,每当发生冲突时就换一个散列函数,相信总有一个能够解决冲突的。这种方法能使关键字不产生聚集,但是代价就是增加了计算时间。是不是很简单啊。
|
||||
|
||||
#### 链地址法
|
||||
|
||||
下面我们再设想以下情景。
|
||||
|
||||
> 袁记菜馆内,铃铃铃,铃铃铃电话铃又响了,那个大鹏又来订房间了。
|
||||
>
|
||||
> 大鹏:老袁啊,我一会去你那吃个饭,还是上回那个包间
|
||||
>
|
||||
> 袁厨:大鹏你下回能不能早点说啊,又没人订走了,这回是老王订的
|
||||
>
|
||||
> 大鹏:老王这个老东西啊,反正也是熟人,你再给我整个桌子,我拼在他后面吧
|
||||
|
||||
不好意思啊各位同学,信鸽最近太贵了还没来得及买。上面的情景就是模拟我们的新的处理冲突的方法链地址法。
|
||||
|
||||
上面我们都是遇到冲突之后,就换地方。那么我们有没有不换地方的办法呢?那就是我们现在说的链地址法。
|
||||
|
||||
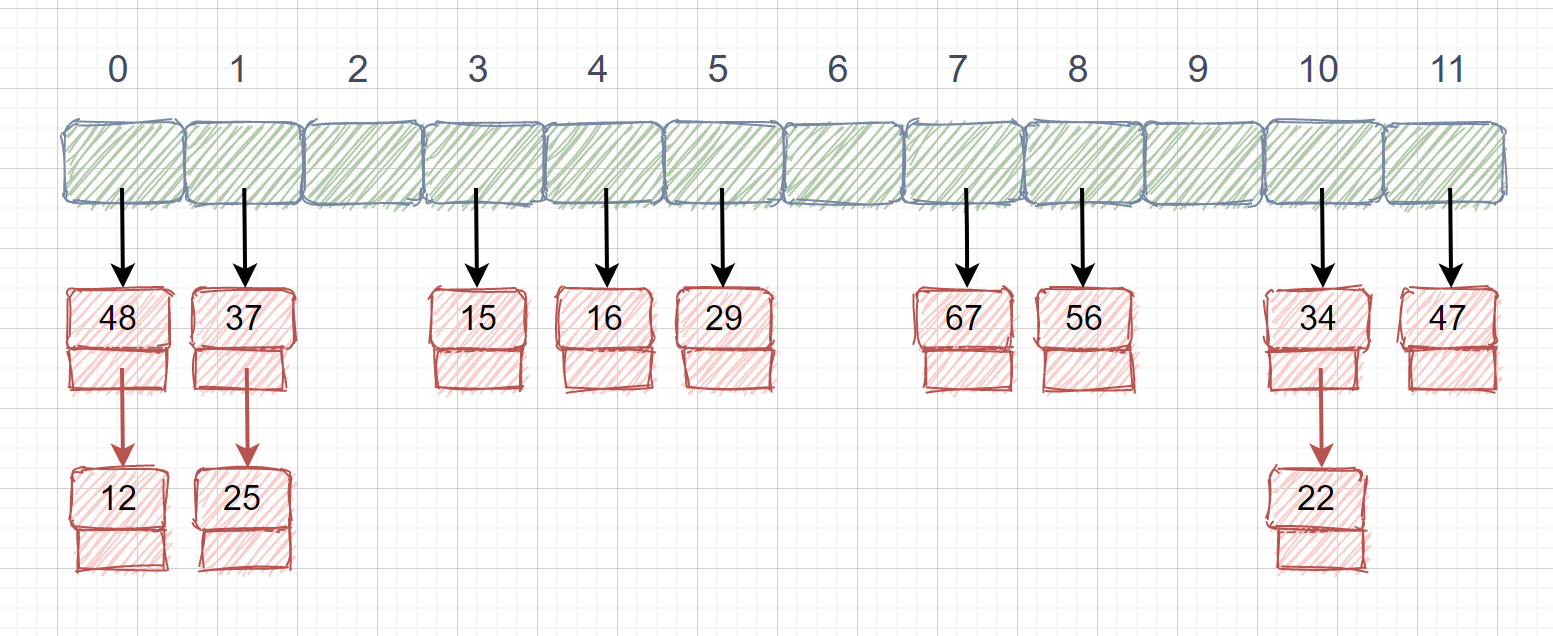
还记得我们说过得同义词吗?就是 key 不同 f(key) 相同的情况,我们将这些同义词存储在一个单链表中,这种表叫做同义词子表,散列表中只存储同义词子表的头指针。我们还是用刚才的例子,关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为12,我们再用散列函数 **f(key) = key mod 12。**我们用了链地址法之后就再也不存在冲突了,无论有多少冲突,我们只需在同义词子表中添加结点即可。下面我们看下链地址法的存储情况。
|
||||
|
||||
|
||||
|
||||
链地址法虽然能够不产生冲突,但是也带来了查找时需要遍历单链表的性能消耗,有得必有失嘛。
|
||||
|
||||
|
||||
|
||||
#### 公共溢出区法
|
||||
|
||||
下面我们再来看一种新的方法,这回大鹏又要来吃饭了。
|
||||
|
||||
> 袁记菜馆内.....
|
||||
>
|
||||
> 袁厨:呦,这是什么风把你给刮来了,咋没开你的大奔啊。
|
||||
>
|
||||
> 大鹏:哎呀妈呀,别那么多废话了,我快饿死了,你快给我找个位置,我要吃点饭。
|
||||
>
|
||||
> 袁厨:你来的,太不巧了,咱们的店已经满了,你先去旁边的小屋看会电视,等有空了我再叫你。小屋里面还有几个和你一样来晚的,你们一起看吧。
|
||||
>
|
||||
> 大鹏:电视?看电视?
|
||||
|
||||
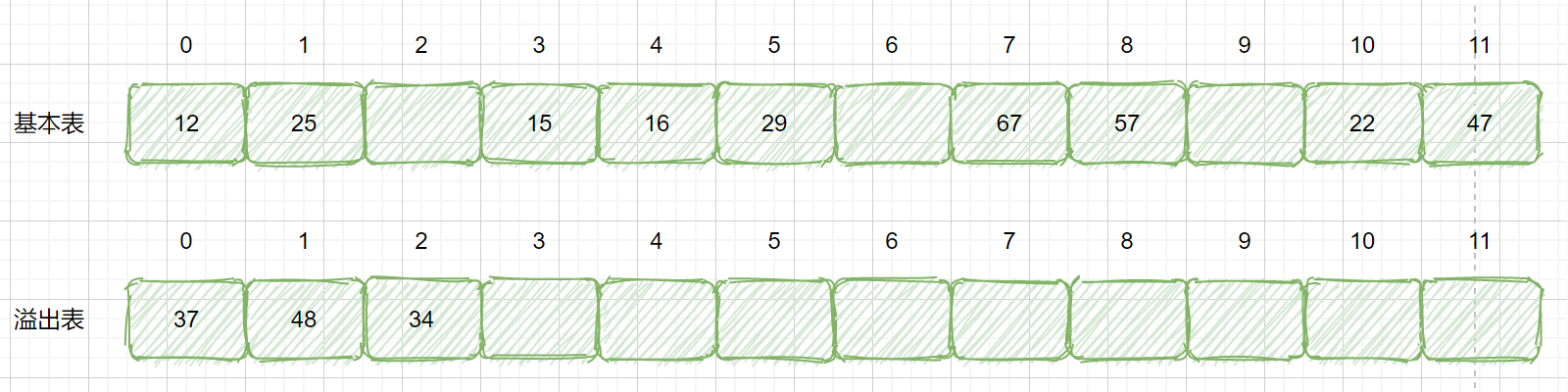
上面得情景就是模拟我们的公共溢出区法,这也是很好理解的,你不是冲突吗?那冲突的各位我先给你安排个地方呆着,这样你就有地方住了。我们为所有冲突的关键字建立了一个公共的溢出区来存放。
|
||||
|
||||
|
||||
|
||||
那么我们怎么进行查找呢?我们首先通过散列函数计算出散列地址后,先于基本表对比,如果不相等再到溢出表去顺序查找。这种解决冲突的方法,对于冲突很少的情况性能还是非常高的。
|
||||
|
||||
### 散列表查找算法(线性探测法)
|
||||
|
||||
下面我们来看一下散列表查找算法的实现
|
||||
|
||||
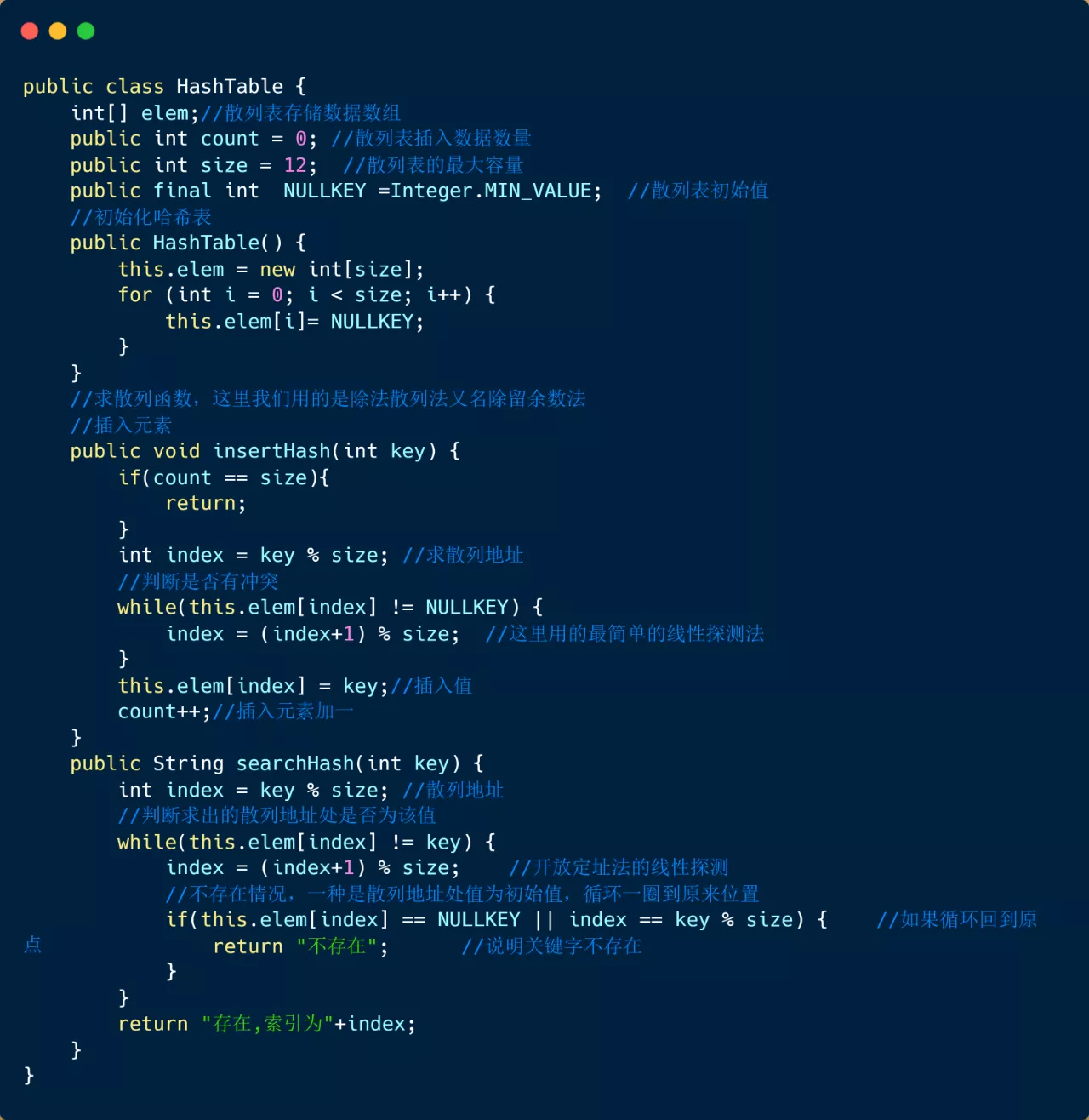
首先需要定义散列列表的结构以及一些相关常数,其中elem代表散列表数据存储数组,count代表的是当前插入元素个数,size代表哈希表容量,NULLKEY散列表初始值,然后我们如果查找成功就返回索引,如果不存在该元素就返回元素不存在。
|
||||
|
||||
我们将哈希表初始化,为数组元素赋初值。
|
||||
|
||||

|
||||
|
||||
插入操作的具体步骤:
|
||||
|
||||
(1)通过哈希函数(除法散列法),将 key 转化为数组下标
|
||||
|
||||
(2)如果该下标中没有元素,则插入,否则说明有冲突,则利用线性探测法处理冲突。详细步骤见注释
|
||||
|
||||

|
||||
|
||||
查找操作的具体步骤:
|
||||
|
||||
(1)通过哈希函数(同插入时一样),将 key 转成数组下标
|
||||
|
||||
(2)通过数组下标找到 key值,如果 key 一致,则查找成功,否则利用线性探测法继续查找。
|
||||
|
||||

|
||||
|
||||
下面我们来看一下完整代码
|
||||
|
||||
|
||||
|
||||
### 散列表性能分析
|
||||
|
||||
如果没有冲突的话,散列查找是我们查找中效率最高的,时间复杂度为O(1),但是没有冲突的情况是一种理想情况,那么散列查找的平均查找长度取决于哪些方面呢?
|
||||
|
||||
**1.散列函数是否均匀**
|
||||
|
||||
我们在上文说到,可以通过设计散列函数减少冲突,但是由于不同的散列函数对一组关键字产生冲突可能性是相同的,因此我们可以不考虑它对平均查找长度的影响。
|
||||
|
||||
**2.处理冲突的方法**
|
||||
|
||||
相同关键字,相同散列函数,不同处理冲突方式,会使平均查找长度不同,比如我们线性探测有时会堆积,则不如二次探测法好,因为链地址法处理冲突时不会产生任何堆积,因而具有最佳的平均查找性能
|
||||
|
||||
**3.散列表的装填因子**
|
||||
|
||||
本来想在上文中提到装填因子的,但是后来发现即使没有说明也不影响我们对哈希表的理解,下面我们来看一下装填因子的总结
|
||||
|
||||
> 装填因子 α = 填入表中的记录数 / 散列表长度
|
||||
|
||||
散列因子则代表着散列表的装满程度,表中记录越多,α就越大,产生冲突的概率就越大。我们上面提到的例子中 表的长度为12,填入记录数为6,那么此时的 α = 6 / 12 = 0.5 所以说当我们的 α 比较大时再填入元素那么产生冲突的可能性就非常大了。所以说散列表的平均查找长度取决于装填因子,而不是取决于记录数。所以说我们需要做的就是选择一个合适的装填因子以便将平均查找长度限定在一个范围之内。
|
||||
|
||||
> 各位如果能感觉到这个文章写的很用心的话,能给您带来一丢丢帮助的话,能麻烦您给这个文章点个赞吗?这样我就巨有动力写下去啦。
|
||||
|
||||
> 另外大家如果需要其他精选算法题的动图解析,大家可以微信关注下 【袁厨的算法小屋】,我是袁厨一个酷爱做饭所以自己考取了厨师证的菜鸡程序员,会一直用心写下去的,感谢支持!
|
||||
@@ -0,0 +1,123 @@
|
||||
## KMP算法(Knuth-Morris-Pratt)
|
||||
|
||||
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
|
||||
|
||||
我们先来看一个实例
|
||||
|
||||

|
||||
|
||||
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
|
||||
|
||||
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
|
||||
|
||||
在上面的例子中我们提到了一个名词,**最长公共前后缀**,这个是什么意思呢?下面我们通过一个较简单的例子进行描述。
|
||||
|
||||

|
||||
|
||||
此时我们在红色阴影处匹配失败,绿色为匹配成功部分,则我们观察匹配成功的部分。
|
||||
|
||||
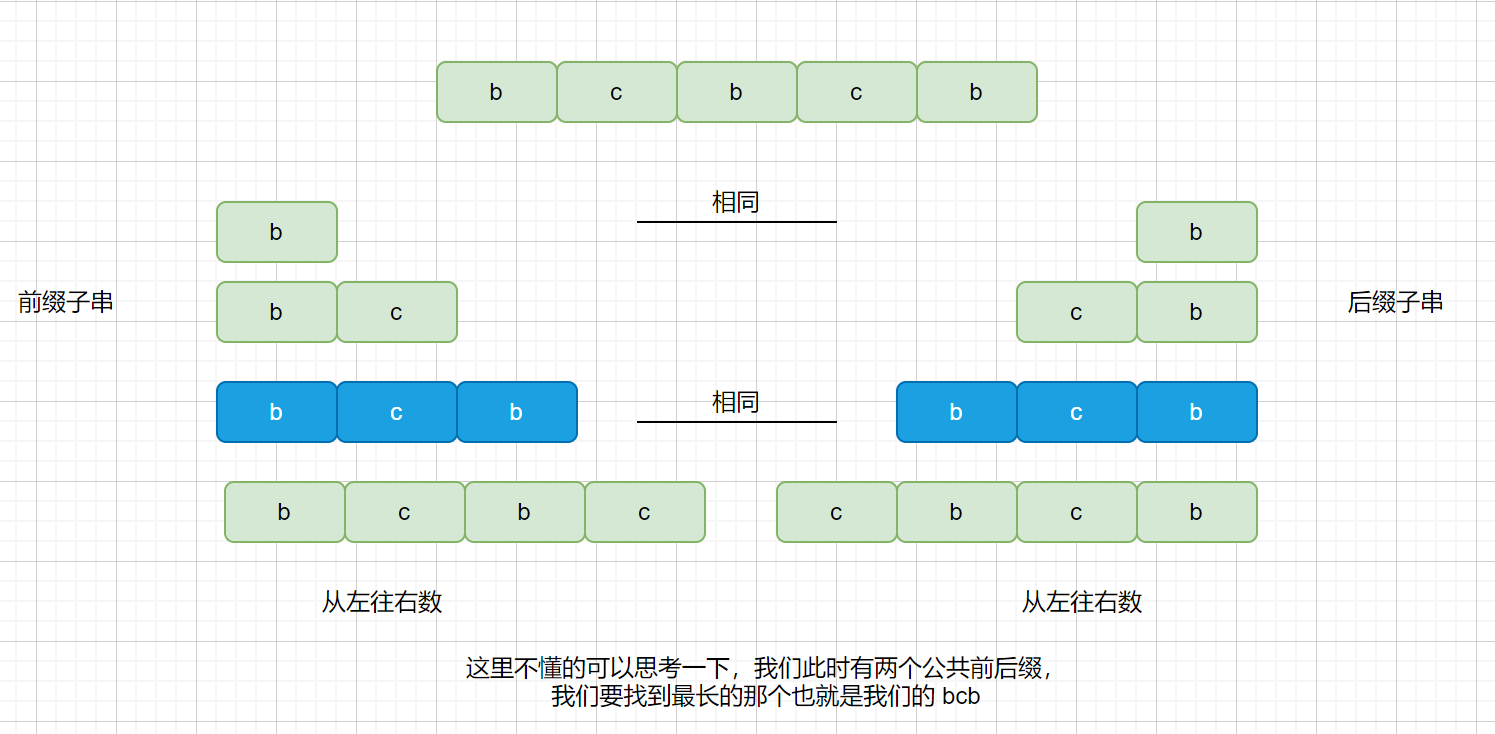
我们来看一下匹配成功部分的所有前缀
|
||||
|
||||
|
||||
|
||||
我们的最长公共前后缀如下图,则我们需要这样移动
|
||||
|
||||

|
||||
|
||||
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
||||
|
||||
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
|
||||
|
||||
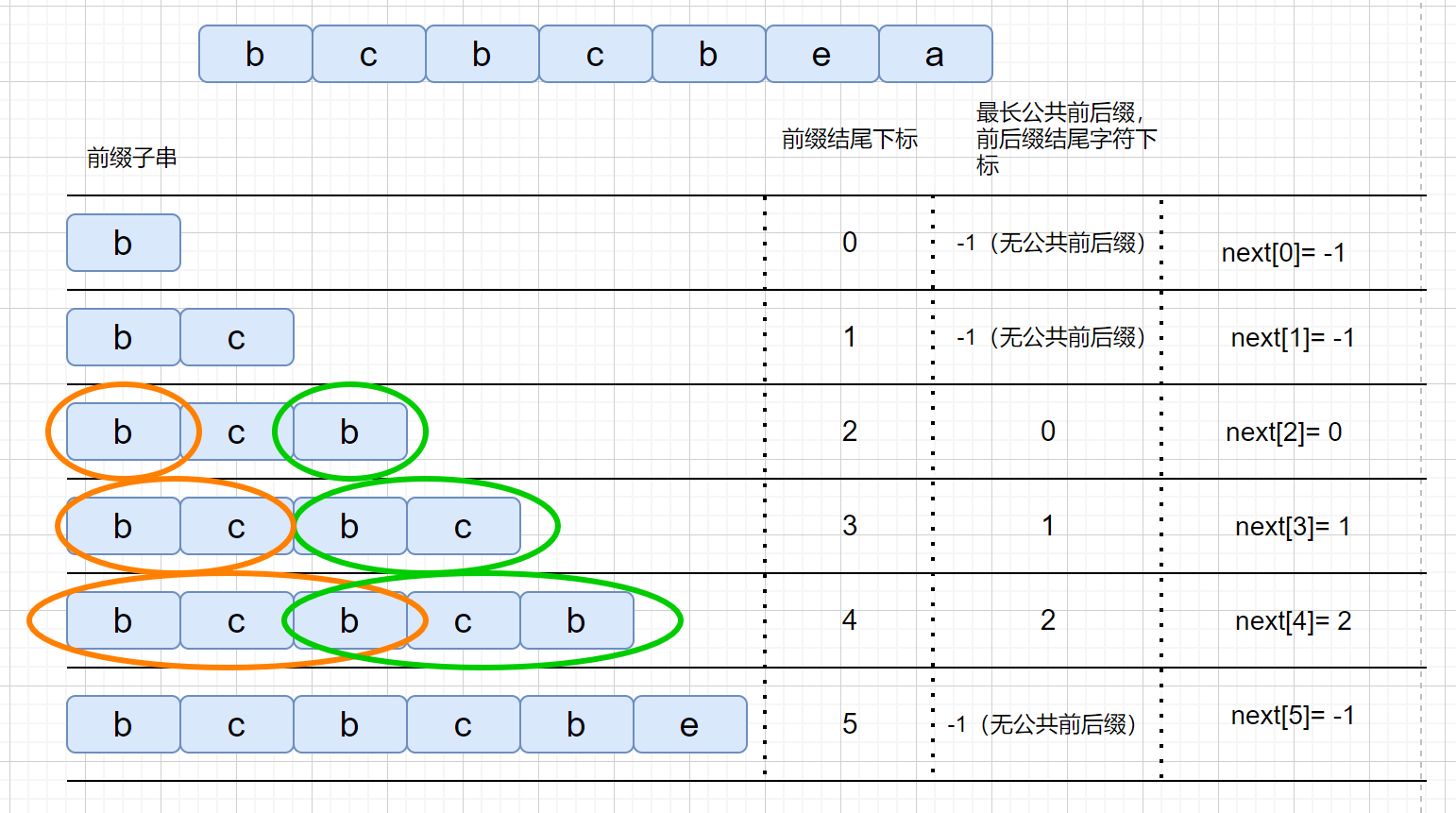
next 数组存的咱们最长公共前后缀中,前缀的结尾字符下标。是不是感觉有点别扭,我们通过一个例子进行说明。
|
||||
|
||||
|
||||
|
||||
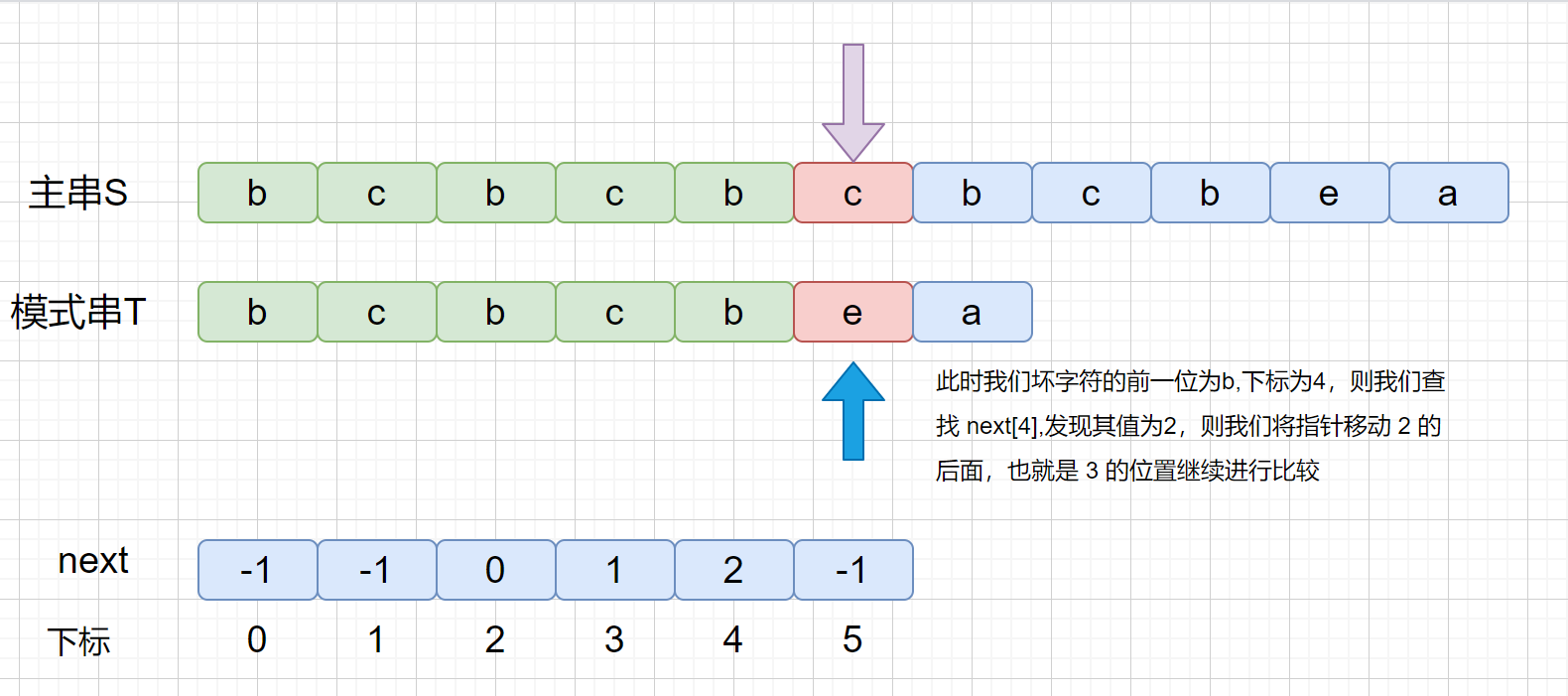
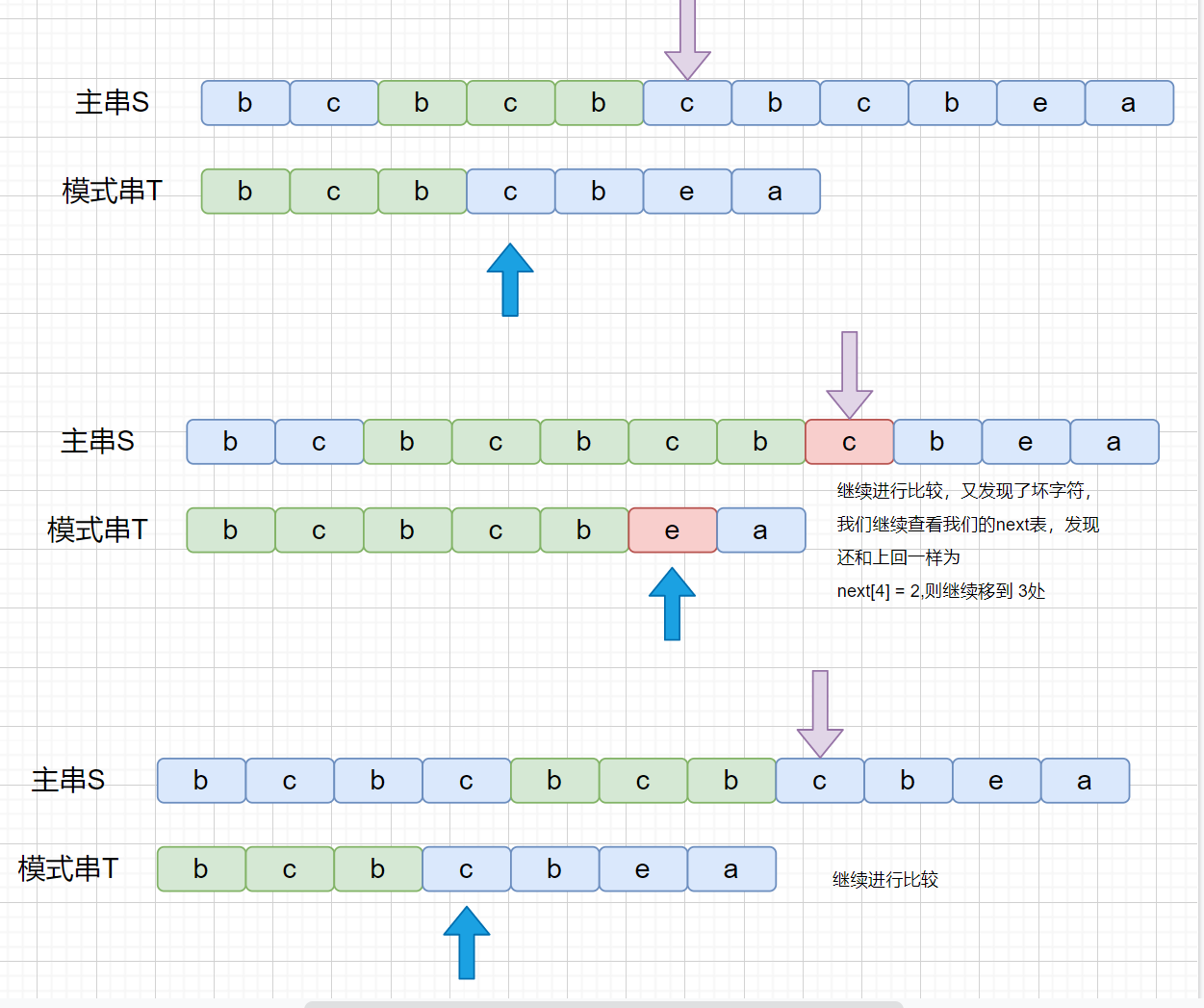
我们知道 next 数组之后,我们的 KMP 算法实现起来就很容易啦,另外我们看一下 next 数组到底是干什么用的。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
剩下的就不用说啦,完全一致啦,咱们将上面这个例子,翻译成和咱们开头对应的动画大家看一下。
|
||||
|
||||

|
||||
|
||||
下面我们看一下代码,标有详细注释,大家认真看呀。
|
||||
|
||||
**注:很多教科书的 next 数组表示方式不一致,理解即可**
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
//两种特殊情况
|
||||
if (needle.length() == 0) {
|
||||
return 0;
|
||||
}
|
||||
if (haystack.length() == 0) {
|
||||
return -1;
|
||||
}
|
||||
// char 数组
|
||||
char[] hasyarr = haystack.toCharArray();
|
||||
char[] nearr = needle.toCharArray();
|
||||
//长度
|
||||
int halen = hasyarr.length;
|
||||
int nelen = nearr.length;
|
||||
//返回下标
|
||||
return kmp(hasyarr,halen,nearr,nelen);
|
||||
|
||||
}
|
||||
public int kmp (char[] hasyarr, int halen, char[] nearr, int nelen) {
|
||||
//获取next 数组
|
||||
int[] next = next(nearr,nelen);
|
||||
int j = 0;
|
||||
for (int i = 0; i < halen; ++i) {
|
||||
//发现不匹配的字符,然后根据 next 数组移动指针,移动到最大公共前后缀的,
|
||||
//前缀的后一位,和咱们移动模式串的含义相同
|
||||
while (j > 0 && hasyarr[i] != nearr[j]) {
|
||||
j = next[j - 1] + 1;
|
||||
//超出长度时,可以直接返回不存在
|
||||
if (nelen - j + i > halen) {
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
//如果相同就将指针同时后移一下,比较下个字符
|
||||
if (hasyarr[i] == nearr[j]) {
|
||||
++j;
|
||||
}
|
||||
//遍历完整个模式串,返回模式串的起点下标
|
||||
if (j == nelen) {
|
||||
return i - nelen + 1;
|
||||
}
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
//这一块比较难懂,不想看的同学可以忽略,了解大致含义即可,或者自己调试一下,看看运行情况
|
||||
//我会每一步都写上注释
|
||||
public int[] next (char[] needle,int len) {
|
||||
//定义 next 数组
|
||||
int[] next = new int[len];
|
||||
// 初始化
|
||||
next[0] = -1;
|
||||
int k = -1;
|
||||
for (int i = 1; i < len; ++i) {
|
||||
//我们此时知道了 [0,i-1]的最长前后缀,但是k+1的指向的值和i不相同时,我们则需要回溯
|
||||
//因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标(即长度)
|
||||
//就要找 k+1前一个元素在next数组里的值,即next[k+1]
|
||||
while (k != -1 && needle[k + 1] != needle[i]) {
|
||||
k = next[k];
|
||||
}
|
||||
// 相同情况,就是 k的下一位,和 i 相同时,此时我们已经知道 [0,i-1]的最长前后缀
|
||||
//然后 k - 1 又和 i 相同,最长前后缀加1,即可
|
||||
if (needle[k+1] == needle[i]) {
|
||||
++k;
|
||||
}
|
||||
next[i] = k;
|
||||
|
||||
}
|
||||
return next;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
486
gif-algorithm/数据结构和算法/字符串匹配算法.md
Normal file
486
gif-algorithm/数据结构和算法/字符串匹配算法.md
Normal file
@@ -0,0 +1,486 @@
|
||||
|
||||
|
||||
> 为保证代码严谨性,文中所有代码均在 leetcode 刷题网站 AC ,大家可以放心食用。
|
||||
|
||||
皇上生辰之际,举国同庆,袁记菜馆作为天下第一饭店,所以被选为这次庆典的菜品供应方,这次庆典对于袁记菜馆是一项前所未有的挑战,毕竟是第一次给皇上庆祝生辰,稍有不慎就是掉脑袋的大罪,整个袁记菜馆内都在紧张的布置着。此时突然有一个店小二慌慌张张跑到袁厨面前汇报,到底发生了什么事,让店小二如此慌张呢?
|
||||
|
||||
袁记菜馆内
|
||||
|
||||
店小二:不好了不好了,掌柜的,出大事了。
|
||||
|
||||
袁厨:发生什么事了,慢慢说,如此慌张,成何体统。(开店开久了,架子出来了哈)
|
||||
|
||||
店小二:皇上按照咱们菜单点了 666 道菜,但是咱们做西湖醋鱼的师傅请假回家结婚了,不知道皇上有没有点这道菜,如果点了这道菜,咱们做不出来,那咱们店可就完了啊。
|
||||
|
||||
(袁厨听了之后,吓得一屁股坐地上了,缓了半天说道)
|
||||
|
||||
袁厨:别说那么多了,快给我找找皇上点的菜里面,有没有这道菜!
|
||||
|
||||
找了很久,并且核对了很多遍,最后确认皇上没有点这道菜。菜馆内的人都松了一口气
|
||||
|
||||
通过上面的一个例子,让我们简单了解了字符串匹配。
|
||||
|
||||
字符串匹配:设 S 和 T 是给定的两个串,在主串 S 中找到模式串 T 的过程称为字符串匹配,如果在主串 S 中找到 模式串 T ,则称匹配成功,函数返回 T 在 S 中首次出现的位置,否则匹配不成功,返回 -1。
|
||||
|
||||
例:
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
在上图中,我们试图找到模式 T = baab,在主串 S = abcabaabcabac 中第一次出现的位置,即为红色阴影部分, T 第一次在 S 中出现的位置下标为 4 ( 字符串的首位下标是 0 ),所以返回 4。如果模式串 T 没有在主串 S 中出现,则返回 -1。
|
||||
|
||||
解决上面问题的算法我们称之为字符串匹配算法,今天我们来介绍三种字符串匹配算法,大家记得打卡呀,说不准面试的时候就问到啦。
|
||||
|
||||
## BF算法(Brute Force)
|
||||
|
||||
这个算法很容易理解,就是我们将模式串和主串进行比较,一致时则继续比较下一字符,直到比较完整个模式串。不一致时则将模式串后移一位,重新从模式串的首位开始对比,重复刚才的步骤下面我们看下这个方法的动图解析,看完肯定一下就能搞懂啦。
|
||||
|
||||
视频详解
|
||||
|
||||
**因为不可以放置视频,所以想看视频的同学,可以去看公众号原文,那里有视频**
|
||||
|
||||
通过上面的代码是不是一下就将这个算法搞懂啦,下面我们用这个算法来解决下面这个经典题目吧。
|
||||
|
||||
### leetcdoe 28. 实现 strStr()
|
||||
|
||||
#### 题目描述
|
||||
|
||||
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
|
||||
|
||||
示例 1:
|
||||
|
||||
> 输入: haystack = "hello", needle = "ll"
|
||||
> 输出: 2
|
||||
|
||||
示例 2:
|
||||
|
||||
> 输入: haystack = "aaaaa", needle = "bba"
|
||||
> 输出: -1
|
||||
|
||||
#### 题目解析
|
||||
|
||||
其实这个题目很容易理解,但是我们需要注意的是一下几点,比如我们的模式串为 0 时,应该返回什么,我们的模式串长度大于主串长度时,应该返回什么,也是我们需要注意的地方。下面我们来看一下题目代码吧。
|
||||
|
||||
#### 题目代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
int haylen = haystack.length();
|
||||
int needlen = needle.length();
|
||||
//特殊情况
|
||||
if (haylen < needlen) {
|
||||
return -1;
|
||||
}
|
||||
if (needlen == 0) {
|
||||
return 0;
|
||||
}
|
||||
//主串
|
||||
for (int i = 0; i < haylen - needlen + 1; ++i) {
|
||||
int j;
|
||||
//模式串
|
||||
for (j = 0; j < needlen; j++) {
|
||||
//不符合的情况,直接跳出,主串指针后移一位
|
||||
if (haystack.charAt(i+j) != needle.charAt(j)) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
//匹配成功
|
||||
if (j == needlen) {
|
||||
return i;
|
||||
}
|
||||
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
我们看一下BF算法的另一种算法(显示回退),其实原理一样,就是对代码进行了一下修改,只要是看完咱们的动图,这个也能够一下就能看懂,大家可以结合下面代码中的注释和动图进行理解。
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
//i代表主串指针,j模式串
|
||||
int i,j;
|
||||
//主串长度和模式串长度
|
||||
int halen = haystack.length();
|
||||
int nelen = needle.length();
|
||||
//循环条件,这里只有 i 增长
|
||||
for (i = 0 , j = 0; i < halen && j < nelen; ++i) {
|
||||
//相同时,则移动 j 指针
|
||||
if (haystack.charAt(i) == needle.charAt(j)) {
|
||||
++j;
|
||||
} else {
|
||||
//不匹配时,将 j 重新指向模式串的头部,将 i 本次匹配的开始位置的下一字符
|
||||
i -= j;
|
||||
j = 0;
|
||||
}
|
||||
}
|
||||
//查询成功时返回索引,查询失败时返回 -1;
|
||||
int renum = j == nelen ? i - nelen : -1;
|
||||
return renum;
|
||||
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
## BM算法(Boyer-Moore)
|
||||
|
||||
我们刚才说过了 BF 算法,但是 BF 算法是有缺陷的,比如我们下面这种情况
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
如上图所示,如果我们利用 BF 算法,遇到不匹配字符时,每次右移一位模式串,再重新从头进行匹配,我们观察一下,我们的模式串 abcdex 中每个字符都不一样,但是我们第一次进行字符串匹配时,abcde 都匹配成功,到 x 时失败,又因为模式串每位都不相同,所以我们不需要再每次右移一位,再重新比较,我们可以直接跳过某些步骤。如下图
|
||||
|
||||

|
||||
|
||||
我们可以跳过其中某些步骤,直接到下面这个步骤。那我们是依据什么原则呢?
|
||||
|
||||

|
||||
|
||||
### 坏字符规则
|
||||
|
||||
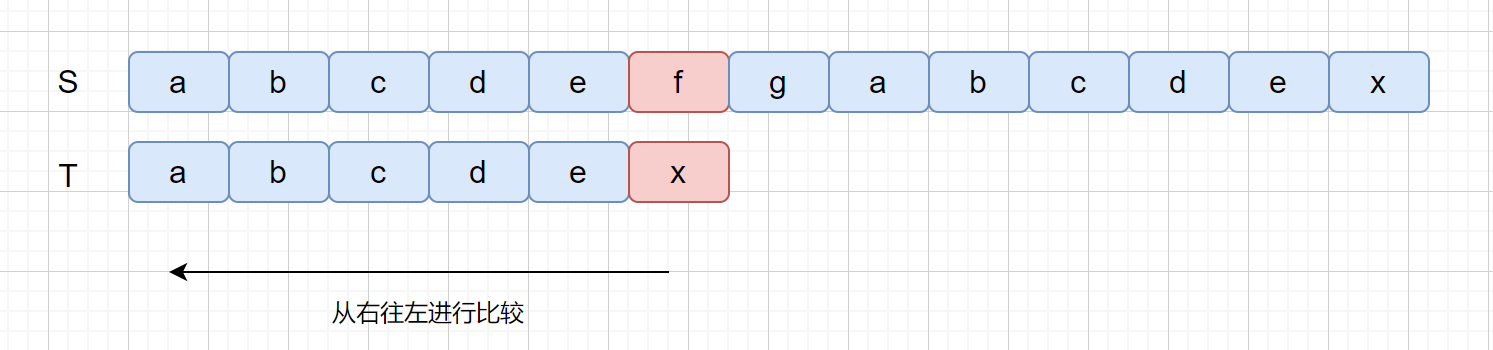
我们之前的 BF 算法是从前往后进行比较 ,BM 算法是从后往前进行比较,我们来看一下具体过程,我们还是利用上面的例子。
|
||||
|
||||

|
||||
|
||||
BM 算法是从后往前进行比较,此时我们发现比较的第一个字符就不匹配,我们将**主串**这个字符称之为**坏字符**,也就是 f ,我们发现坏字符之后,模式串 T 中查找是否含有该字符(f),我们发现并不存在 f,此时我们只需将模式串右移到坏字符的后面一位即可。如下图
|
||||
|
||||

|
||||
|
||||
那我们在模式串中找到坏字符该怎么办呢?
|
||||
|
||||

|
||||
|
||||
此时我们的坏字符为 f ,我们在模式串中,查找发现含有坏字符 f,我们则需要移动模式串 T ,将模式串中的 f 和坏字符对齐。见下图。
|
||||
|
||||

|
||||
|
||||
然后我们继续从右往左进行比较,发现 d 为坏字符,则需要将模式串中的 d 和坏字符对齐。
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
那么我们在来思考一下这种情况,那就是模式串中含有多个坏字符怎么办呢?
|
||||
|
||||

|
||||
|
||||
那么我们为什么要让**最靠右的对应元素与坏字符匹配**呢?如果上面的例子我们没有按照这条规则看下会产生什么问题。
|
||||
|
||||

|
||||
|
||||
如果没有按照我们上述规则,则会**漏掉我们的真正匹配**。我们的主串中是**含有 babac** 的,但是却**没有匹配成功**,所以应该遵守**最靠右的对应字符与坏字符相对**的规则。
|
||||
|
||||
我们上面一共介绍了三种移动情况,分别是下方的模式串中没有发现与坏字符对应的字符,发现一个对应字符,发现两个。这三种情况我们分别移动不同的位数,那我们是根据依据什么来决定移动位数的呢?下面我们给图中的字符加上下标。见下图
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
下面我们来考虑一下这种情况。
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
此时这种情况肯定是不行的,不往右移动,甚至还有可能左移,那么我们有没有什么办法解决这个问题呢?继续往下看吧。
|
||||
|
||||
### 好后缀规则
|
||||
|
||||
好后缀其实也很容易理解,我们之前说过 BM 算法是从右往左进行比较,下面我们来看下面这个例子。
|
||||
|
||||

|
||||
|
||||
这里如果我们按照坏字符进行移动是不合理的,这时我们可以使用好后缀规则,那么什么是好后缀呢?
|
||||
|
||||
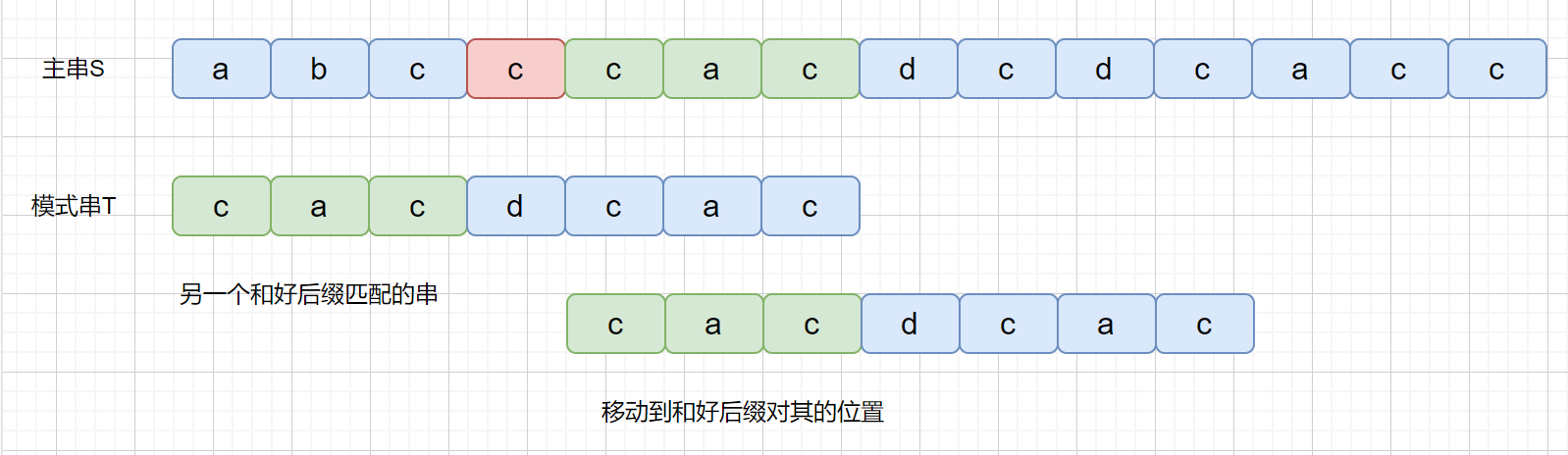
BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已经匹配成功,在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀,此时我们拿它在模式串中查找,如果找到了另一个和好后缀相匹配的串,那我们就将另一个和**好后缀相匹配**的串 ,滑到和好后缀对齐的位置。
|
||||
|
||||
是不是感觉有点拗口,没关系,我们看下图,红色代表坏字符,绿色代表好后缀
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
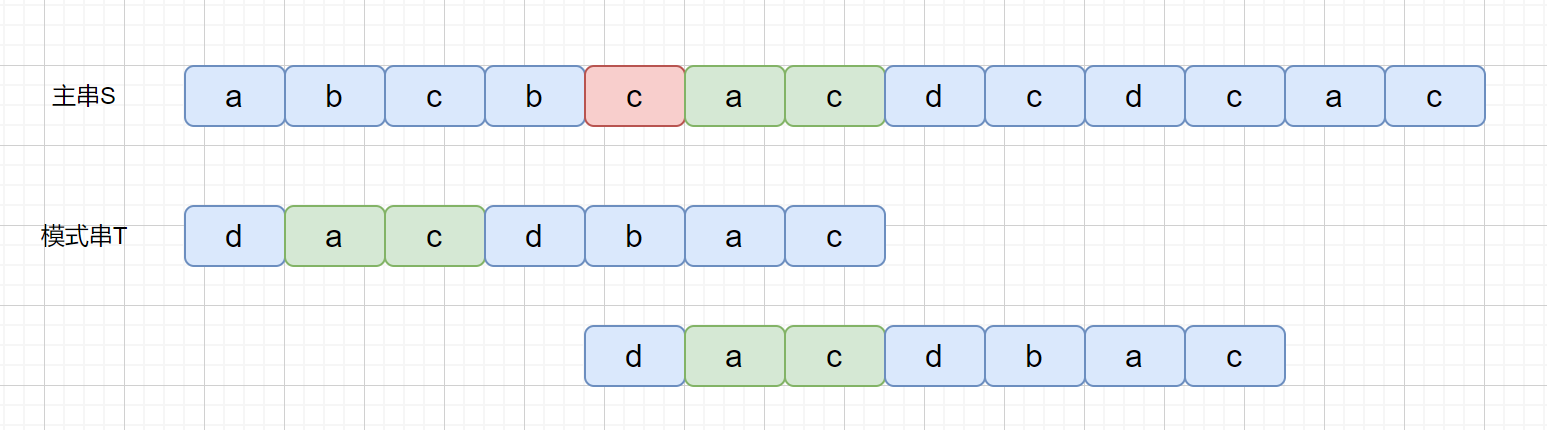
上面那种情况搞懂了,但是我们思考一下下面这种情况
|
||||
|
||||

|
||||
|
||||
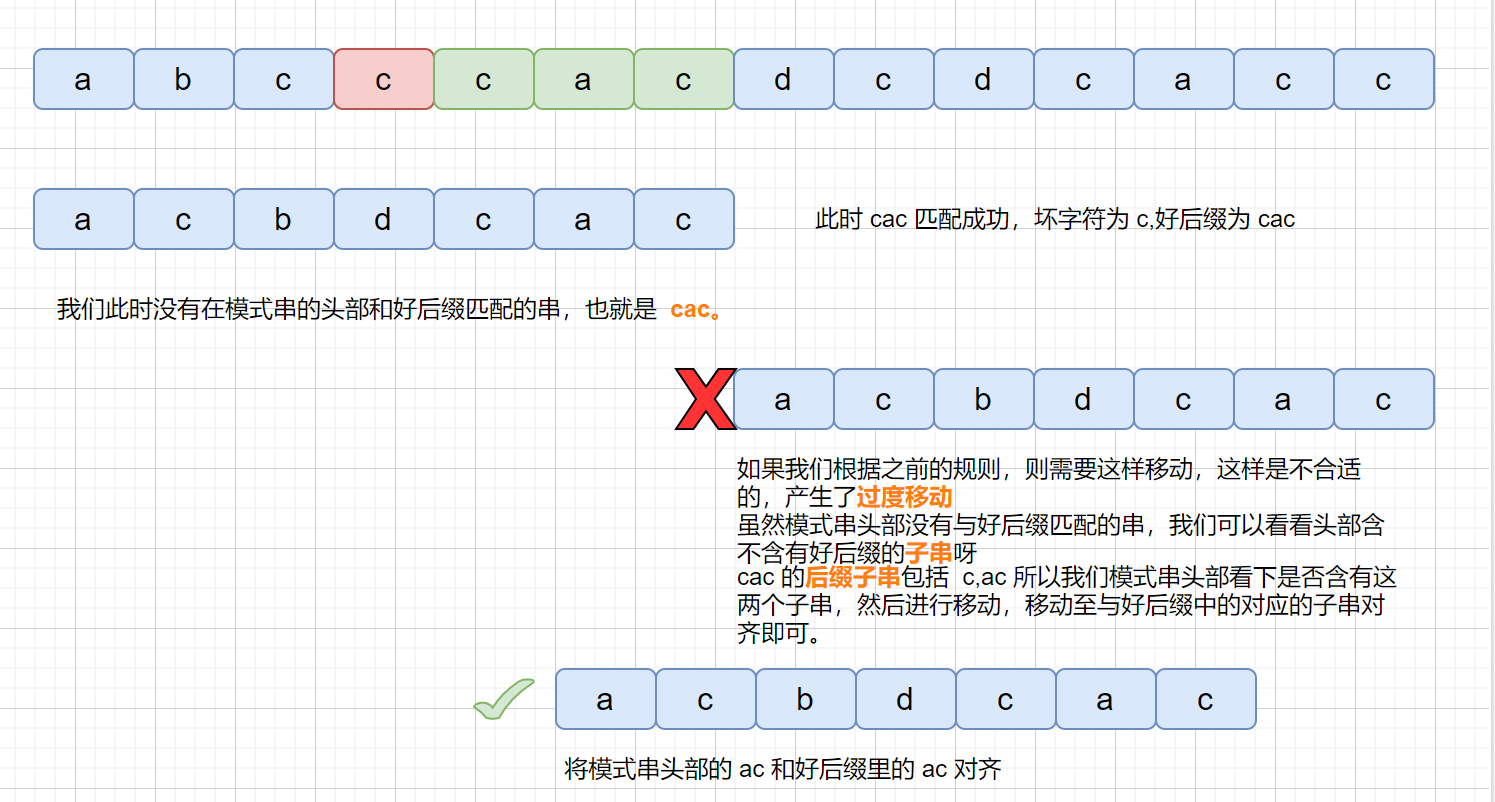
上面我们说到了,如果在模式串的**头部**没有发现好后缀,发现好后缀的子串也可以。但是为什么要强调这个头部呢?
|
||||
|
||||
我们下面来看一下这种情况
|
||||
|
||||

|
||||
|
||||
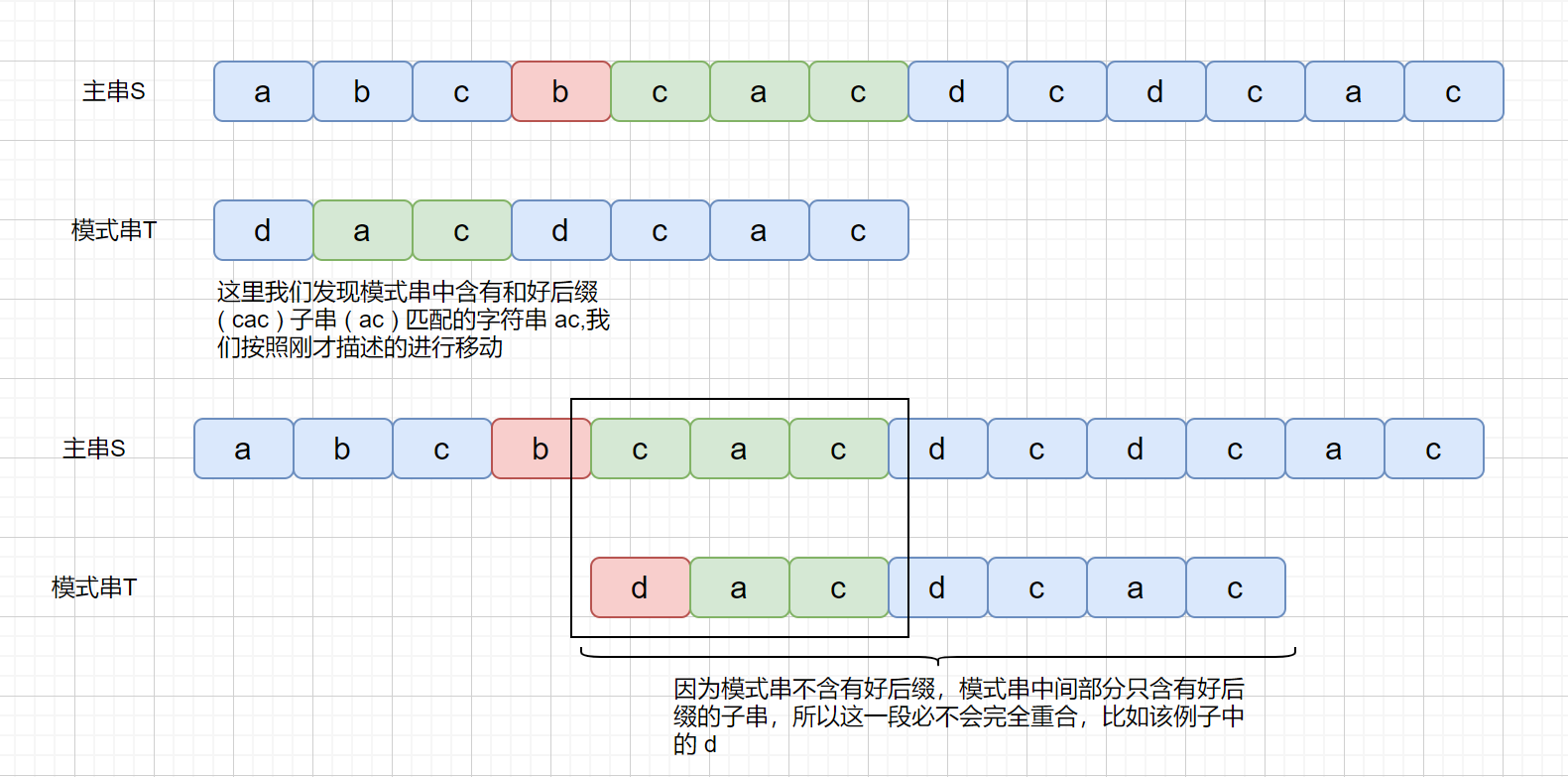
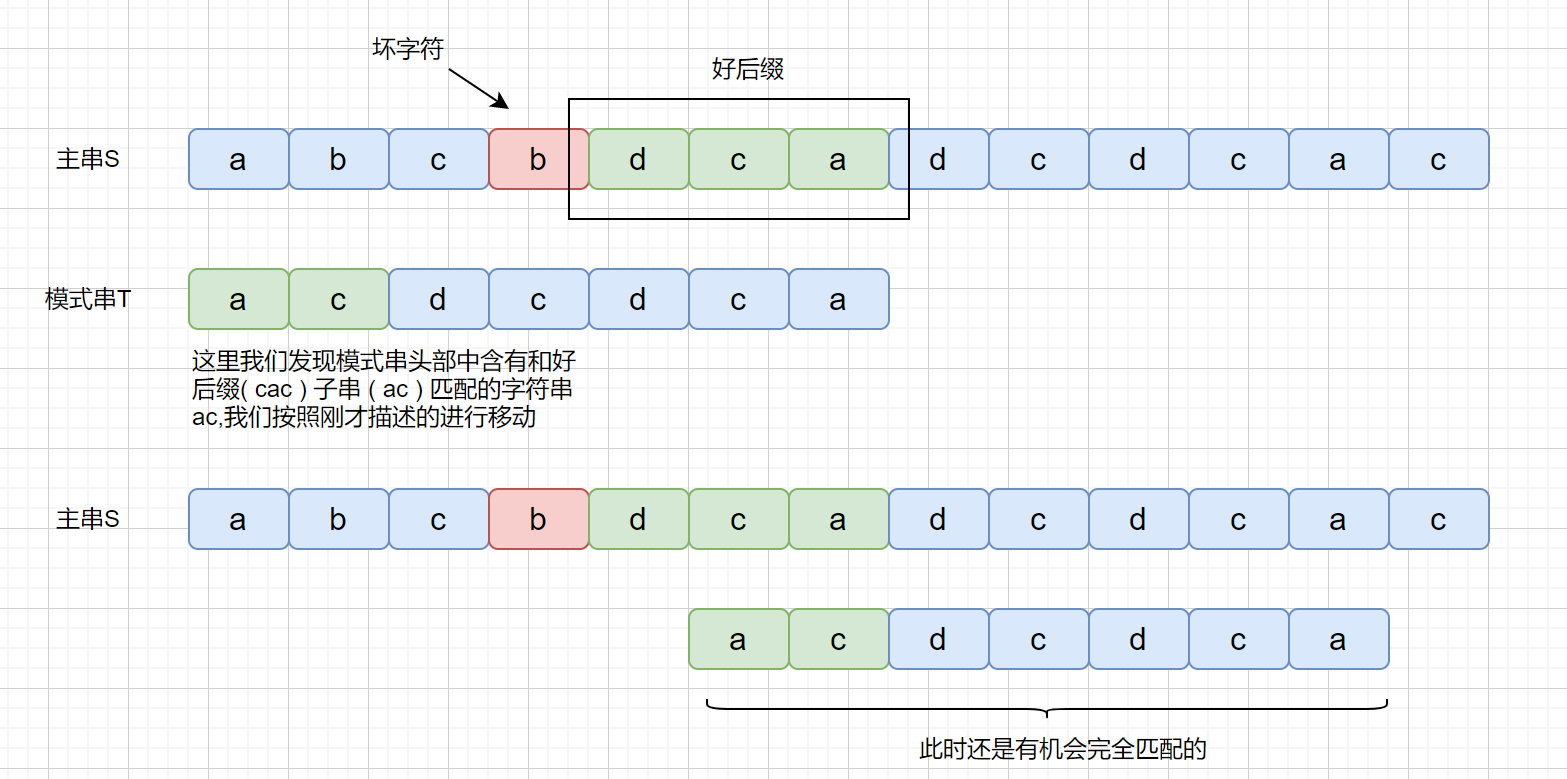
但是当我们在头部发现好后缀的子串时,是什么情况呢?
|
||||
|
||||
|
||||
|
||||
下面我们通过动图来看一下某一例子的具体的执行过程
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
视频
|
||||
|
||||
|
||||
|
||||
说到这里,坏字符和好后缀规则就算说完了,坏字符很容易理解,我们对好后缀总结一下
|
||||
|
||||
1.如果模式串**含有好后缀**,无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次,则以**最右侧的好后缀**为基准。
|
||||
|
||||
2.如果模式串**头部含有**好后缀子串则可以按照规则进行移动,中间部分含有好后缀子串则不可以。
|
||||
|
||||
3.如果在模式串尾部就出现不匹配的情况,即不存在好后缀时,则根据坏字符进行移动,这里有的文章没有提到,是个需要特别注意的地方,我是在这个论文里找到答案的,感兴趣的同学可以看下。
|
||||
|
||||
> Boyer R S,Moore J S. A fast string searching algorithm[J]. Communications of the ACM,1977,10: 762-772.
|
||||
|
||||
|
||||
|
||||
之前我们刚开始说坏字符的时候,是不是有可能会出现负值的情况,即往左移动的情况,所以我们为了解决这个问题,我们可以分别计算好后缀和坏字符往后滑动的位数**(好后缀不为 0 的情况)**,然后取两个数中最大的,作为模式串往后滑动的位数。
|
||||
|
||||

|
||||
|
||||
这破图画起来是真费劲啊。下面我们来看一下算法代码,代码有点长,我都标上了注释也在网站上 AC 了,如果各位感兴趣可以看一下,不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
char[] hay = haystack.toCharArray();
|
||||
char[] need = needle.toCharArray();
|
||||
int haylen = haystack.length();
|
||||
int needlen = need.length;
|
||||
return bm(hay,haylen,need,needlen);
|
||||
}
|
||||
//用来求坏字符情况下移动位数
|
||||
private static void badChar(char[] b, int m, int[] bc) {
|
||||
//初始化
|
||||
for (int i = 0; i < 256; ++i) {
|
||||
bc[i] = -1;
|
||||
}
|
||||
//m 代表模式串的长度,如果有两个 a,则后面那个会覆盖前面那个
|
||||
for (int i = 0; i < m; ++i) {
|
||||
int ascii = (int)b[i];
|
||||
bc[ascii] = i;//下标
|
||||
}
|
||||
}
|
||||
//用来求好后缀条件下的移动位数
|
||||
private static void goodSuffix (char[] b, int m, int[] suffix,boolean[] prefix) {
|
||||
//初始化
|
||||
for (int i = 0; i < m; ++i) {
|
||||
suffix[i] = -1;
|
||||
prefix[i] = false;
|
||||
}
|
||||
for (int i = 0; i < m - 1; ++i) {
|
||||
int j = i;
|
||||
int k = 0;
|
||||
while (j >= 0 && b[j] == b[m-1-k]) {
|
||||
--j;
|
||||
++k;
|
||||
suffix[k] = j + 1;
|
||||
}
|
||||
if (j == -1) prefix[k] = true;
|
||||
}
|
||||
}
|
||||
public static int bm (char[] a, int n, char[] b, int m) {
|
||||
|
||||
int[] bc = new int[256];//创建一个数组用来保存最右边字符的下标
|
||||
badChar(b,m,bc);
|
||||
//用来保存各种长度好后缀的最右位置的数组
|
||||
int[] suffix_index = new int[m];
|
||||
//判断是否是头部,如果是头部则true
|
||||
boolean[] ispre = new boolean[m];
|
||||
goodSuffix(b,m,suffix_index,ispre);
|
||||
int i = 0;//第一个匹配字符
|
||||
//注意结束条件
|
||||
while (i <= n-m) {
|
||||
int j;
|
||||
//从后往前匹配,匹配失败,找到坏字符
|
||||
for (j = m - 1; j >= 0; --j) {
|
||||
if (a[i+j] != b[j]) break;
|
||||
}
|
||||
//模式串遍历完毕,匹配成功
|
||||
if (j < 0) {
|
||||
return i;
|
||||
}
|
||||
//下面为匹配失败时,如何处理
|
||||
//求出坏字符规则下移动的位数,就是我们坏字符下标减最右边的下标
|
||||
int x = j - bc[(int)a[i+j]];
|
||||
int y = 0;
|
||||
//好后缀情况,求出好后缀情况下的移动位数,如果不含有好后缀的话,则按照坏字符来
|
||||
if (y < m-1 && m - 1 - j > 0) {
|
||||
y = move(j, m, suffix_index,ispre);
|
||||
}
|
||||
//移动
|
||||
i = i + Math.max(x,y);
|
||||
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
// j代表坏字符的下标
|
||||
private static int move (int j, int m, int[] suffix_index, boolean[] ispre) {
|
||||
//好后缀长度
|
||||
int k = m - 1 - j;
|
||||
//如果含有长度为 k 的好后缀,返回移动位数,
|
||||
if (suffix_index[k] != -1) return j - suffix_index[k] + 1;
|
||||
//找头部为好后缀子串的最大长度,从长度最大的子串开始
|
||||
for (int r = j + 2; r <= m-1; ++r) {
|
||||
//如果是头部
|
||||
if (ispre[m-r] == true) {
|
||||
return r;
|
||||
}
|
||||
}
|
||||
//如果没有发现好后缀匹配的串,或者头部为好后缀子串,则移动到 m 位,也就是匹配串的长度
|
||||
return m;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
我们来理解一下我们代码中用到的两个数组,因为两个规则的移动位数,只与模式串有关,与主串无关,所以我们可以提前求出每种情况的移动情况,保存到数组中。
|
||||
|
||||

|
||||
|
||||
## KMP算法(Knuth-Morris-Pratt)
|
||||
|
||||
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
|
||||
|
||||
我们先来看一个实例
|
||||
|
||||
视频
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
|
||||
|
||||
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
|
||||
|
||||
在上面的例子中我们提到了一个名词,**最长公共前后缀**,这个是什么意思呢?下面我们通过一个较简单的例子进行描述。
|
||||
|
||||

|
||||
|
||||
此时我们在红色阴影处匹配失败,绿色为匹配成功部分,则我们观察匹配成功的部分。
|
||||
|
||||
我们来看一下匹配成功部分的所有前缀
|
||||
|
||||

|
||||
|
||||
我们的最长公共前后缀如下图,则我们需要这样移动
|
||||
|
||||

|
||||
|
||||
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
||||
|
||||
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
|
||||
|
||||
next 数组存的咱们最长公共前后缀中,前缀的结尾字符下标。是不是感觉有点别扭,我们通过一个例子进行说明。
|
||||
|
||||

|
||||
|
||||
我们知道 next 数组之后,我们的 KMP 算法实现起来就很容易啦,另外我们看一下 next 数组到底是干什么用的。
|
||||
|
||||

|
||||
|
||||

|
||||
|
||||
剩下的就不用说啦,完全一致啦,咱们将上面这个例子,翻译成和咱们开头对应的动画大家看一下。
|
||||
|
||||
**因为不可以放置视频,所以想看视频的同学,可以去看公众号原文,那里有视频**
|
||||
|
||||
下面我们看一下代码,标有详细注释,大家认真看呀。
|
||||
|
||||
**注:很多教科书的 next 数组表示方式不一致,理解即可**
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
//两种特殊情况
|
||||
if (needle.length() == 0) {
|
||||
return 0;
|
||||
}
|
||||
if (haystack.length() == 0) {
|
||||
return -1;
|
||||
}
|
||||
// char 数组
|
||||
char[] hasyarr = haystack.toCharArray();
|
||||
char[] nearr = needle.toCharArray();
|
||||
//长度
|
||||
int halen = hasyarr.length;
|
||||
int nelen = nearr.length;
|
||||
//返回下标
|
||||
return kmp(hasyarr,halen,nearr,nelen);
|
||||
|
||||
}
|
||||
public int kmp (char[] hasyarr, int halen, char[] nearr, int nelen) {
|
||||
//获取next 数组
|
||||
int[] next = next(nearr,nelen);
|
||||
int j = 0;
|
||||
for (int i = 0; i < halen; ++i) {
|
||||
//发现不匹配的字符,然后根据 next 数组移动指针,移动到最大公共前后缀的,
|
||||
//前缀的后一位,和咱们移动模式串的含义相同
|
||||
while (j > 0 && hasyarr[i] != nearr[j]) {
|
||||
j = next[j - 1] + 1;
|
||||
//超出长度时,可以直接返回不存在
|
||||
if (nelen - j + i > halen) {
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
//如果相同就将指针同时后移一下,比较下个字符
|
||||
if (hasyarr[i] == nearr[j]) {
|
||||
++j;
|
||||
}
|
||||
//遍历完整个模式串,返回模式串的起点下标
|
||||
if (j == nelen) {
|
||||
return i - nelen + 1;
|
||||
}
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
//这一块比较难懂,不想看的同学可以忽略,了解大致含义即可,或者自己调试一下,看看运行情况
|
||||
//我会每一步都写上注释
|
||||
public int[] next (char[] needle,int len) {
|
||||
//定义 next 数组
|
||||
int[] next = new int[len];
|
||||
// 初始化
|
||||
next[0] = -1;
|
||||
int k = -1;
|
||||
for (int i = 1; i < len; ++i) {
|
||||
//我们此时知道了 [0,i-1]的最长前后缀,但是k+1的指向的值和i不相同时,我们则需要回溯
|
||||
//因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标(即长度)
|
||||
//就要找 k+1前一个元素在next数组里的值,即next[k+1]
|
||||
while (k != -1 && needle[k + 1] != needle[i]) {
|
||||
k = next[k];
|
||||
}
|
||||
// 相同情况,就是 k的下一位,和 i 相同时,此时我们已经知道 [0,i-1]的最长前后缀
|
||||
//然后 k - 1 又和 i 相同,最长前后缀加1,即可
|
||||
if (needle[k+1] == needle[i]) {
|
||||
++k;
|
||||
}
|
||||
next[i] = k;
|
||||
|
||||
}
|
||||
return next;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这篇文章真的写了很久很久,觉得还不错的话,就麻烦您点个赞吧,大家也可以去我的公众号看我的所有文章,每个都有动图解析,公众号:[袁厨的算法小屋](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/qrcode_for_gh_1f36d2ef6df9_258.5lojyphpkso0.jpg)
|
||||
|
||||
Reference in New Issue
Block a user