mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2025-08-12 17:52:27 +00:00
代码重构 【Github Actions】
This commit is contained in:
@@ -1,8 +1,8 @@
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
>
|
||||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||||
>
|
||||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||||
|
||||
## 查找元素第一个位置和最后一个位置
|
||||
|
||||
@@ -10,8 +10,6 @@
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
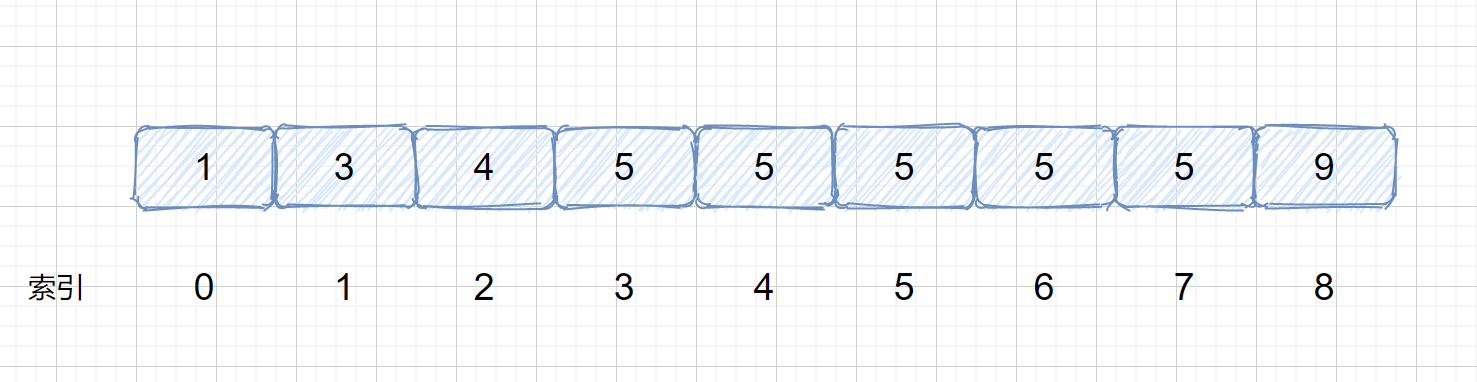
此时我们数组里含有多个 5 ,我们查询是否含有 5 可以很容易查到,但是我们想获取第一个 5 和 最后一个 5 的位置应该怎么实现呢?哦!我们可以使用遍历,当查询到第一个 5 时,我们设立一个指针进行定位,然后到达最后一个 5 时返回,这样我们就能求的第一个和最后一个五了?因为我们这个文章的主题就是二分查找,我们可不可以用二分查找来实现呢?当然是可以的。
|
||||
|
||||
#### [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/)
|
||||
@@ -22,7 +20,6 @@
|
||||
>
|
||||
> 如果数组中不存在目标值 target,返回 [-1, -1]。
|
||||
|
||||
|
||||
示例 1:
|
||||
|
||||
> 输入:nums = [5,7,7,8,8,10], target = 8
|
||||
@@ -53,28 +50,24 @@
|
||||
}else if (nums[mid] > target) {
|
||||
//这里需要注意,移动右指针
|
||||
right = mid - 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
我们只需在这段代码中修改即可,我们再来剖析一下这块代码,nums[mid] == target 时则返回,nums[mid] < target 时则移动左指针,在右区间进行查找, nums[mid] > target时则移动右指针,在左区间内进行查找。
|
||||
我们只需在这段代码中修改即可,我们再来剖析一下这块代码,nums[mid] == target 时则返回,nums[mid] < target 时则移动左指针,在右区间进行查找, nums[mid] > target 时则移动右指针,在左区间内进行查找。
|
||||
|
||||
那么我们思考一下,如果此时我们的 nums[mid] = target ,但是我们不能确定 mid 是否为该目标数的左边界,所以此时我们不可以返回下标。例如下面这种情况。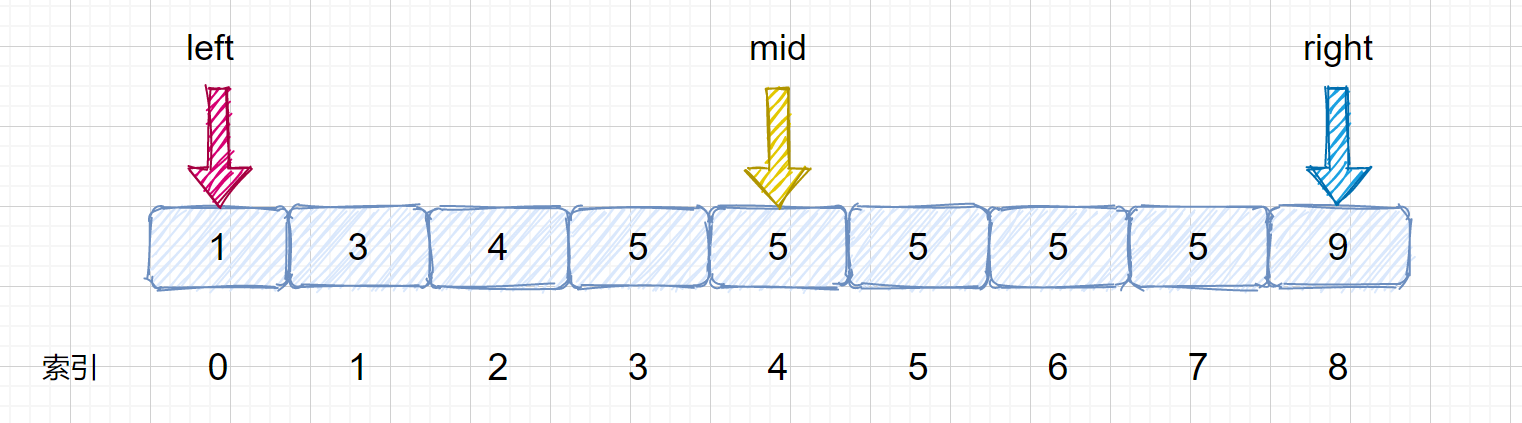
|
||||
|
||||
|
||||
|
||||
此时 mid = 4 ,nums[mid] = 5,但是此时的 mid 指向的并不是第一个 5,所以我们需要继续查找 ,因为我们要找
|
||||
|
||||
的是数的下边界,所以我们需要在 mid 的值的左区间继续寻找 5 ,那我们应该怎么做呢?我们只需在
|
||||
的是数的下边界,所以我们需要在 mid 的值的左区间继续寻找 5 ,那我们应该怎么做呢?我们只需在
|
||||
|
||||
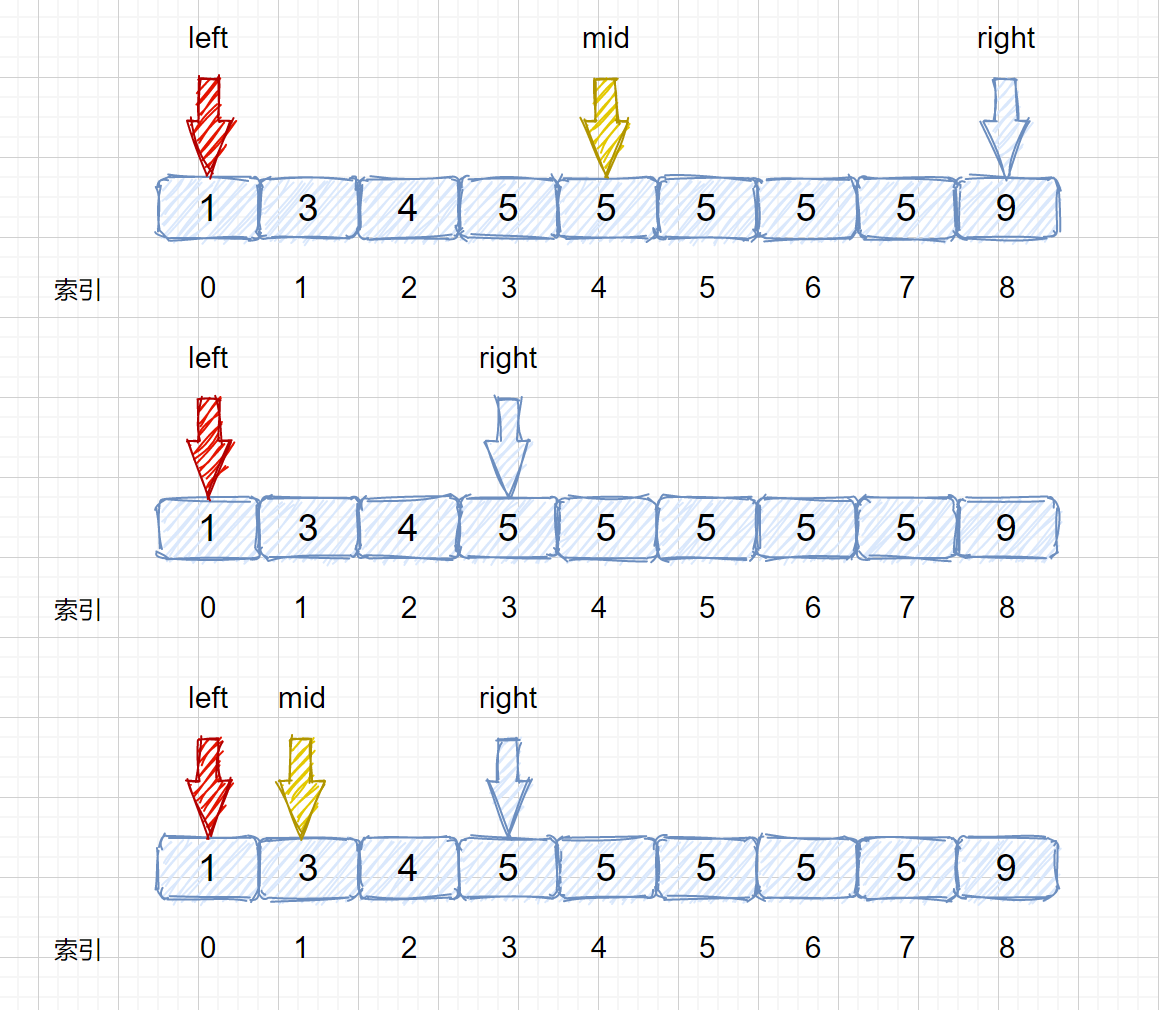
target <= nums[mid] 时,让 right = mid - 1即可,这样我们就可以继续在 mid 的左区间继续找 5 。是不是听着有点绕,我们通过下面这组图进行描述。
|
||||
target <= nums[mid] 时,让 right = mid - 1 即可,这样我们就可以继续在 mid 的左区间继续找 5 。是不是听着有点绕,我们通过下面这组图进行描述。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
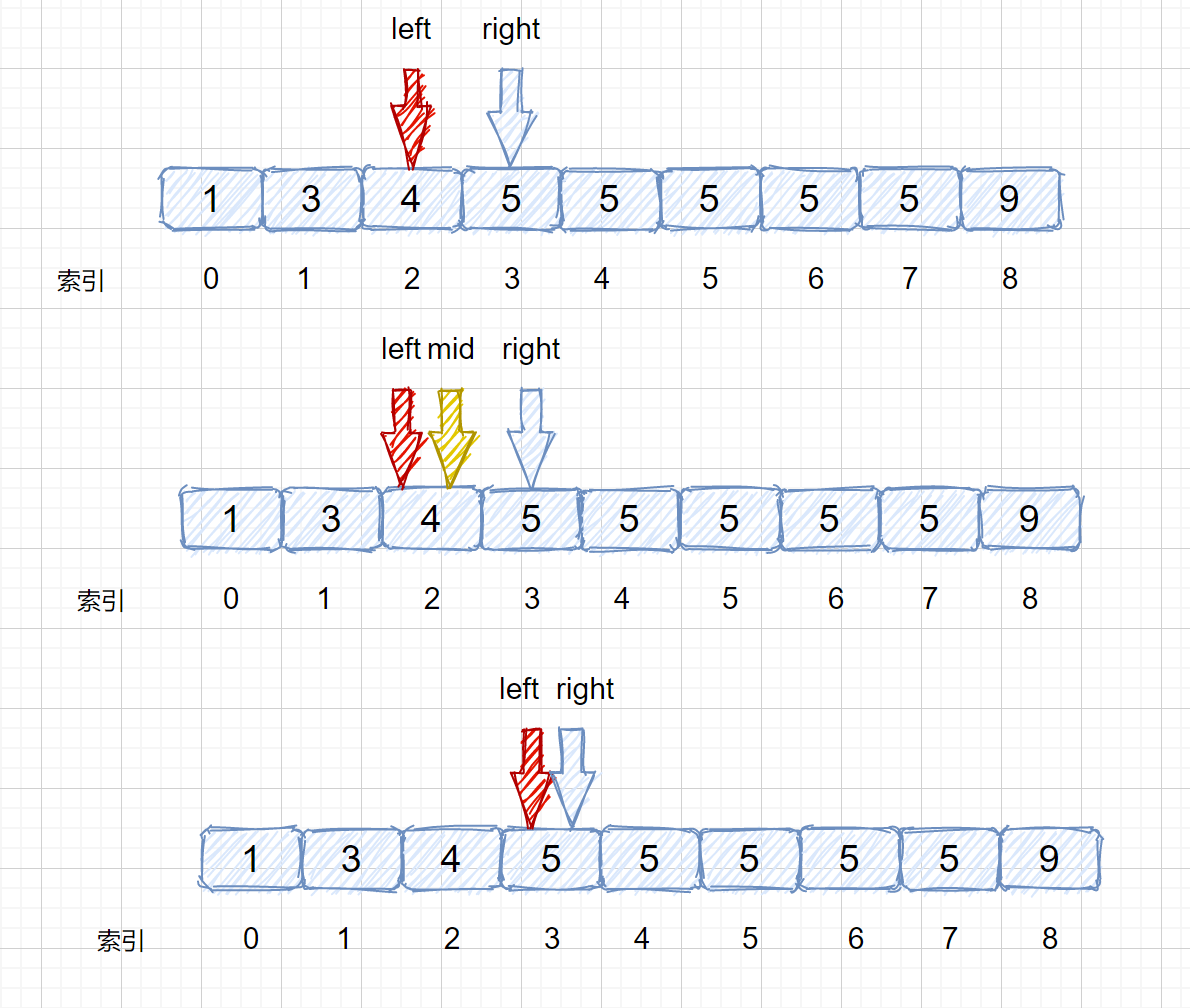
其实原理很简单,就是我们将小于和等于合并在一起处理,当 target <= nums[mid] 时,我们都移动右指针,也就是 right = mid -1,还有一个需要注意的就是,我们计算下边界时最后的返回值为 left ,当上图结束循环时,left = 3,right = 2,返回 left 刚好时我们的下边界。我们来看一下求下边界的具体执行过程。
|
||||
其实原理很简单,就是我们将小于和等于合并在一起处理,当 target <= nums[mid] 时,我们都移动右指针,也就是 right = mid -1,还有一个需要注意的就是,我们计算下边界时最后的返回值为 left ,当上图结束循环时,left = 3,right = 2,返回 left 刚好时我们的下边界。我们来看一下求下边界的具体执行过程。
|
||||
|
||||
**动图解析**
|
||||
|
||||
@@ -100,13 +93,11 @@ int lowerBound(int[] nums, int target) {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
计算上边界时算是和计算上边界时条件相反,
|
||||
|
||||
计算下边界时,当 target <= nums[mid] 时,right = mid -1;target > nums[mid] 时,left = mid + 1;
|
||||
计算下边界时,当 target <= nums[mid] 时,right = mid -1;target > nums[mid] 时,left = mid + 1;
|
||||
|
||||
计算上边界时,当 target < nums[mid] 时,right = mid -1; target >= nums[mid] 时 left = mid + 1;刚好和计算下边界时条件相反,返回right。
|
||||
计算上边界时,当 target < nums[mid] 时,right = mid -1; target >= nums[mid] 时 left = mid + 1;刚好和计算下边界时条件相反,返回 right。
|
||||
|
||||
**计算上边界代码**
|
||||
|
||||
@@ -118,12 +109,12 @@ int upperBound(int[] nums, int target) {
|
||||
int mid = left + ((right - left) >> 1);
|
||||
//移动左指针情况
|
||||
if (target >= nums[mid]) {
|
||||
left = mid + 1;
|
||||
left = mid + 1;
|
||||
//移动右指针情况
|
||||
}else if (target < nums[mid]) {
|
||||
right = mid - 1;
|
||||
}
|
||||
|
||||
|
||||
}
|
||||
return left;
|
||||
}
|
||||
@@ -135,7 +126,7 @@ int upperBound(int[] nums, int target) {
|
||||
class Solution {
|
||||
public int[] searchRange (int[] nums, int target) {
|
||||
int upper = upperBound(nums,target);
|
||||
int low = lowerBound(nums,target);
|
||||
int low = lowerBound(nums,target);
|
||||
//不存在情况
|
||||
if (upper < low) {
|
||||
return new int[]{-1,-1};
|
||||
@@ -163,16 +154,15 @@ class Solution {
|
||||
//计算上边界
|
||||
int upperBound(int[] nums, int target) {
|
||||
int left = 0, right = nums.length - 1;
|
||||
while (left <= right) {
|
||||
while (left <= right) {
|
||||
int mid = left + ((right - left) >> 1);
|
||||
if (target >= nums[mid]) {
|
||||
left = mid + 1;
|
||||
left = mid + 1;
|
||||
}else if (target < nums[mid]) {
|
||||
right = mid - 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
return right;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
Reference in New Issue
Block a user