mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2025-08-06 07:31:57 +00:00
代码重构 【Github Actions】
This commit is contained in:
@@ -4,30 +4,28 @@ Morris 遍历利用树的左右孩子为空(大量空闲指针),实现空
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
看完视频,是不是感觉自己搞懂了,又感觉自己没搞懂,哈哈,咱们继续往下看。
|
||||
|
||||
|
||||
|
||||
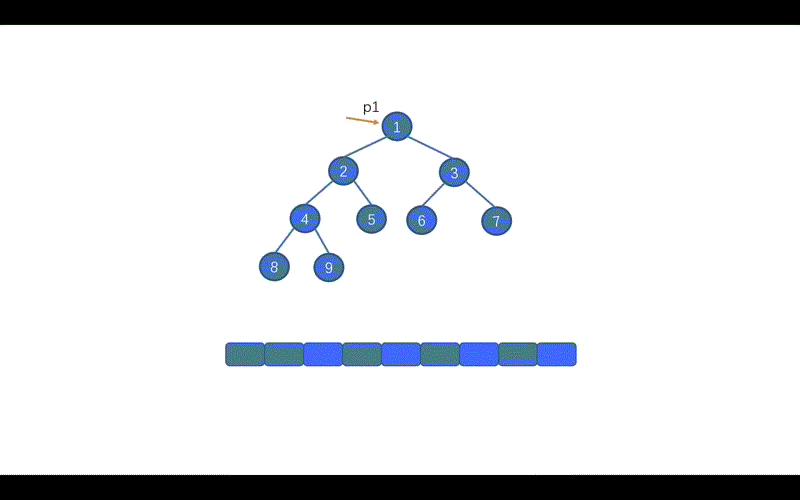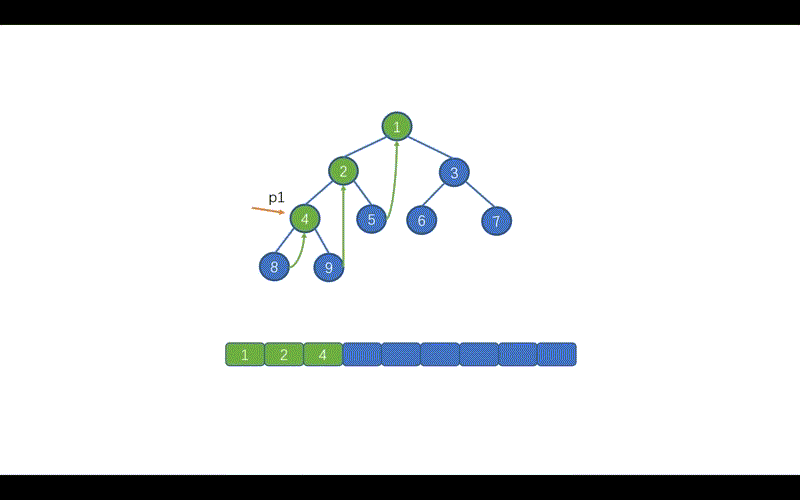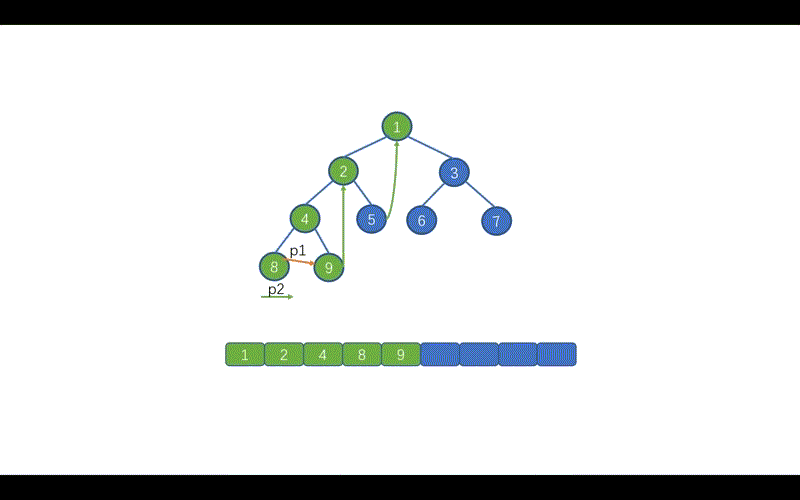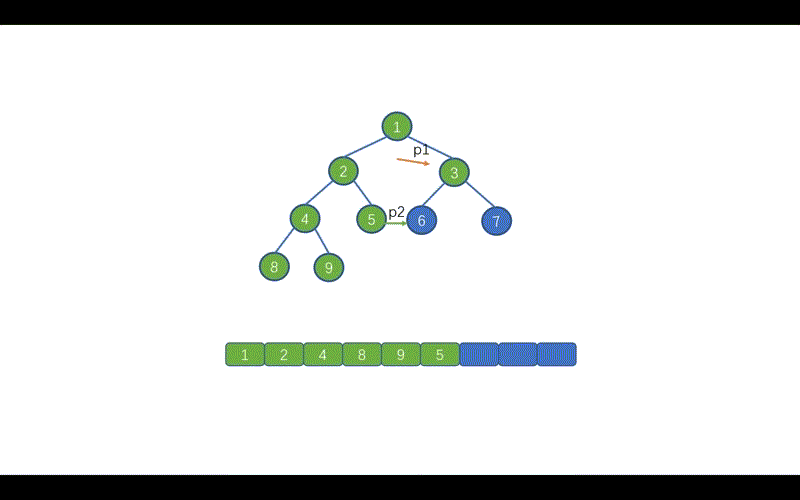
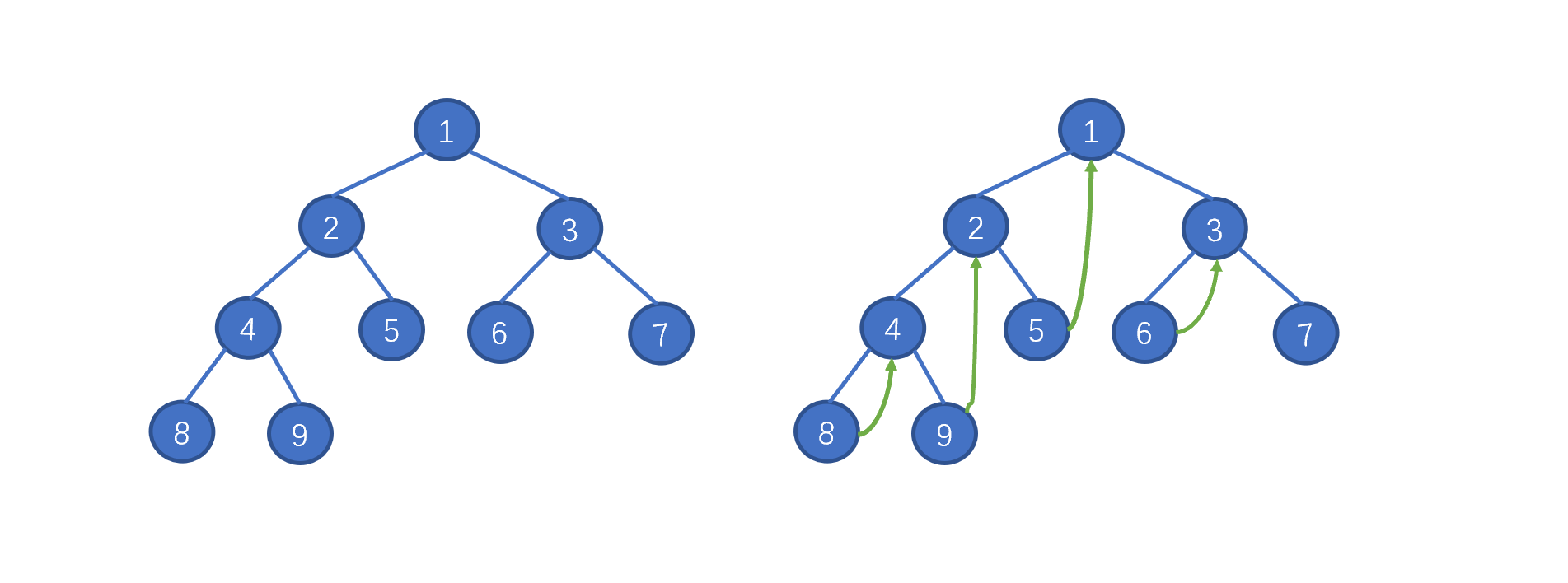
我们之前说的,Morris 遍历利用了`树中大量空闲指针的特性`,我们需要`找到当前节点的左子树中的最右边的叶子节点`,将该叶子节点的 right 指向当前节点。例如当前节点为2,其左子树中的最右节点为 9 ,则在 9 节点添加一个 right 指针指向 2。
|
||||
我们之前说的,Morris 遍历利用了`树中大量空闲指针的特性`,我们需要`找到当前节点的左子树中的最右边的叶子节点`,将该叶子节点的 right 指向当前节点。例如当前节点为 2,其左子树中的最右节点为 9 ,则在 9 节点添加一个 right 指针指向 2。
|
||||
|
||||
其实上图中的 Morris 遍历遵循两个原则,我们在动画中也能够得出。
|
||||
其实上图中的 Morris 遍历遵循两个原则,我们在动画中也能够得出。
|
||||
|
||||
1. 当 p1.left == null 时,p1 = p1.right。(这也就是我们为什么要给叶子节点添加 right 指针的原因)
|
||||
|
||||
2. 如果 p1.left != null,找到 p1 左子树上最右的节点。(也就是我们的 p2 最后停留的位置),此时我们又可以分为两种情况,一种是叶子节点添加 right 指针的情况,一种是去除叶子节点 right 指针的情况。
|
||||
|
||||
3. - 如果 p2 的 right 指针指向空,让其指向 p1,p1向左移动,即 p1 = p1.left
|
||||
3. - 如果 p2 的 right 指针指向空,让其指向 p1,p1 向左移动,即 p1 = p1.left
|
||||
- 如果 p2 的 right 指针指向 p1,让其指向空,(为了防止重复执行,则需要去掉 right 指针)p1 向右移动,p1 = p1.right。
|
||||
|
||||
这时你可以结合咱们刚才提到的两个原则,再去看一遍动画,并代入规则进行模拟,差不多就能完全搞懂啦。
|
||||
|
||||
下面我们来对动画中的内容进行拆解 ,
|
||||
|
||||
首先 p1 指向 root节点
|
||||
首先 p1 指向 root 节点
|
||||
|
||||
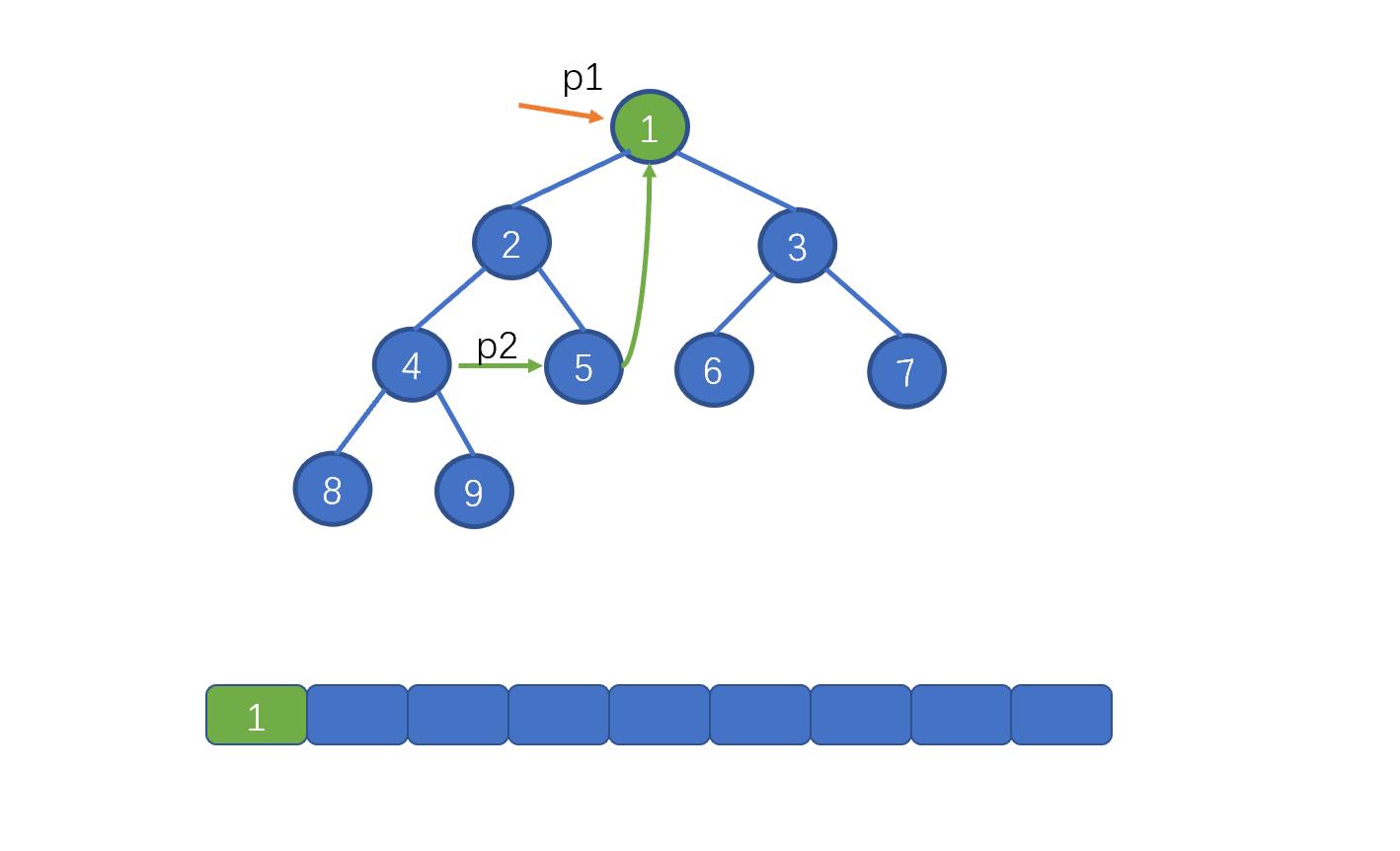
p2 = p1.left,下面我们需要通过 p2 找到 p1的左子树中的最右节点。即节点 5,然后将该节点的 right 指针指向 root。并记录 root 节点的值。
|
||||
p2 = p1.left,下面我们需要通过 p2 找到 p1 的左子树中的最右节点。即节点 5,然后将该节点的 right 指针指向 root。并记录 root 节点的值。
|
||||
|
||||
|
||||
|
||||
@@ -37,14 +35,10 @@ p2 = p1.left ,即节点 4 ,找到 p1 的左子树中的最右叶子节点,
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
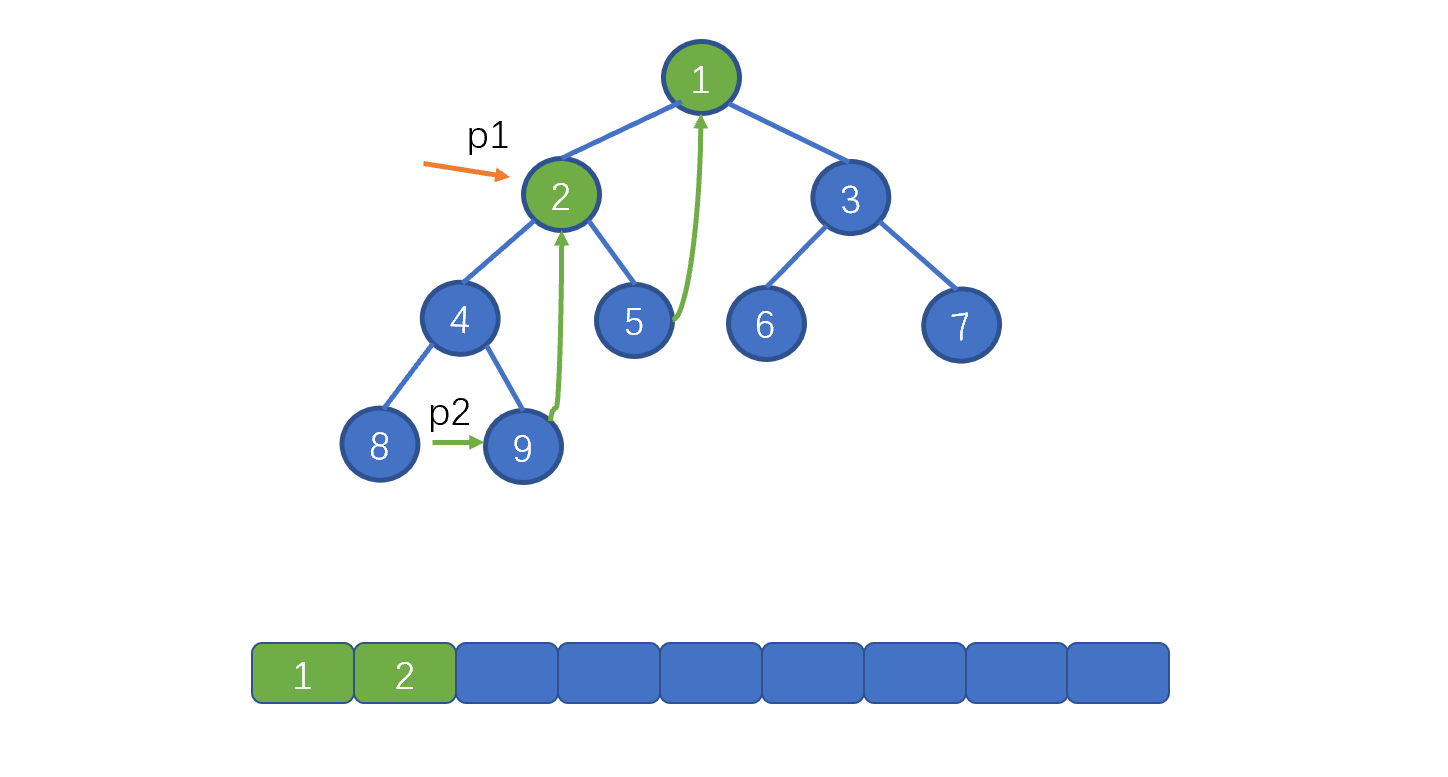
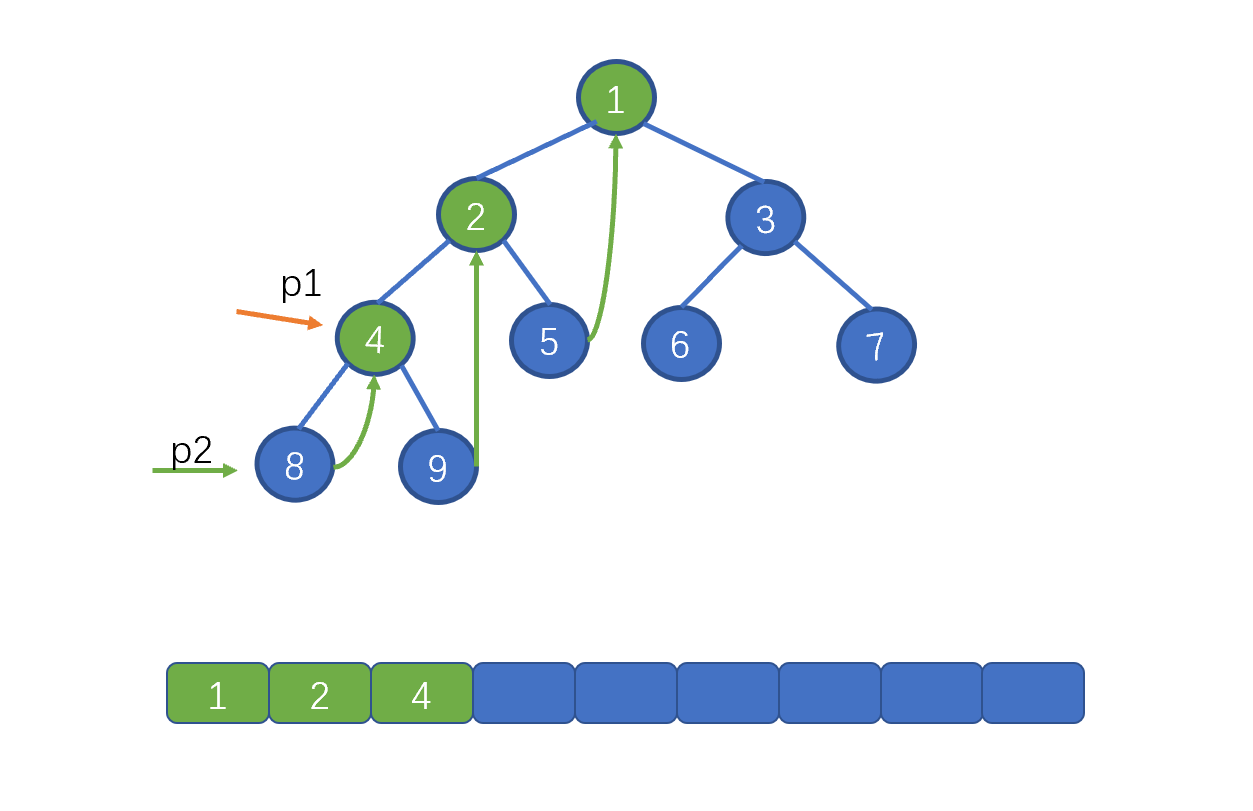
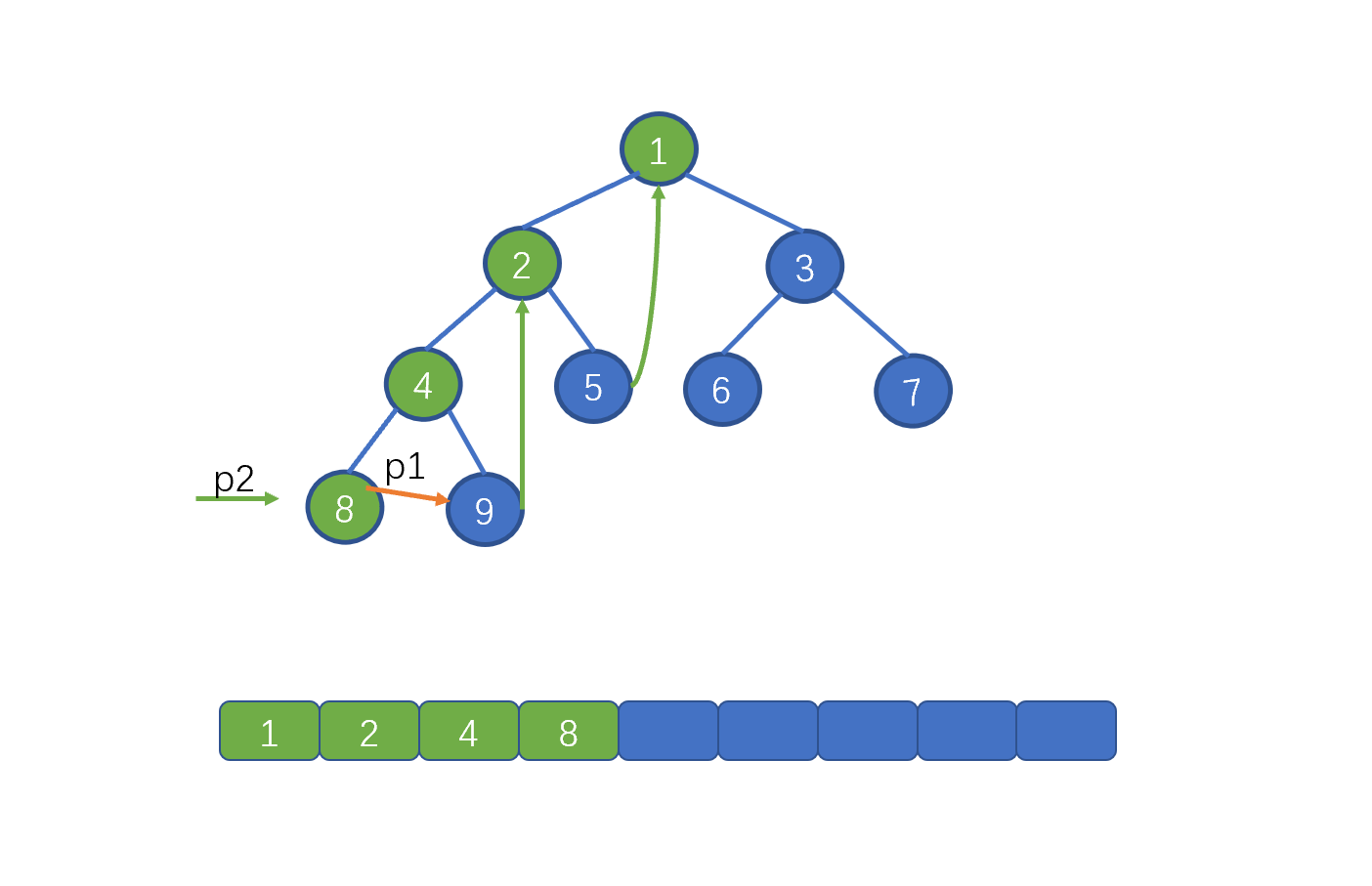
继续向左移动 p1,即 p1 = p1.left,p2 = p1.left。 也就是节点 8。并将该节点的 right 指针指向 p1。
|
||||
继续向左移动 p1,即 p1 = p1.left,p2 = p1.left。 也就是节点 8。并将该节点的 right 指针指向 p1。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
我们发现这一步给前两步是一样的,都是找到叶子节点,将其 right 指针指向 p1,此时我们完成了添加 right 指针的过程,下面我们继续往下看。
|
||||
|
||||
我们继续移动 p1 指针,p1 = p1.left。p2 = p.left。此时我们发现 p2 == null,即下图
|
||||
@@ -59,7 +53,7 @@ p2 = p1.left ,即节点 4 ,找到 p1 的左子树中的最右叶子节点,
|
||||
|
||||
|
||||
|
||||
下面则继续移动 p1 ,按照规则继续移动即可,遇到的情况已经在上面做出了举例,所以下面我们就不继续赘述啦,如果还不是特别理解的同学,可以再去看一遍动画加深下印象。
|
||||
下面则继续移动 p1 ,按照规则继续移动即可,遇到的情况已经在上面做出了举例,所以下面我们就不继续赘述啦,如果还不是特别理解的同学,可以再去看一遍动画加深下印象。
|
||||
|
||||
时间复杂度 O(n),空间复杂度 O(1)
|
||||
|
||||
@@ -140,4 +134,4 @@ class Solution {
|
||||
}
|
||||
```
|
||||
|
||||
好啦,今天就看到这里吧,咱们下期见!
|
||||
好啦,今天就看到这里吧,咱们下期见!
|
||||
|
||||
Reference in New Issue
Block a user