代码重构 【Github Actions】

animation-simulation/数据结构和算法/冒泡排序.md

@@ -1,8 +1,8 @@
-> 如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友  **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ，备注  github  + 题目 + 问题  向我反馈
+> 如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ，备注 github + 题目 + 问题 向我反馈
 >
 > 感谢支持，该仓库会一直维护，希望对各位有一丢丢帮助。
 >
-> 另外希望手机阅读的同学可以来我的 <u>[**公众号：袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。 
+> 另外希望手机阅读的同学可以来我的 <u>[**公众号：袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
 
 **写在前面**
 
@@ -36,8 +36,6 @@
 
 ![](https://cdn.jsdelivr.net/gh/tan45du/github.io.phonto2@master/myphoto/微信截图_20210119171706.xe5v3t5wjw0.png)
 
-
-
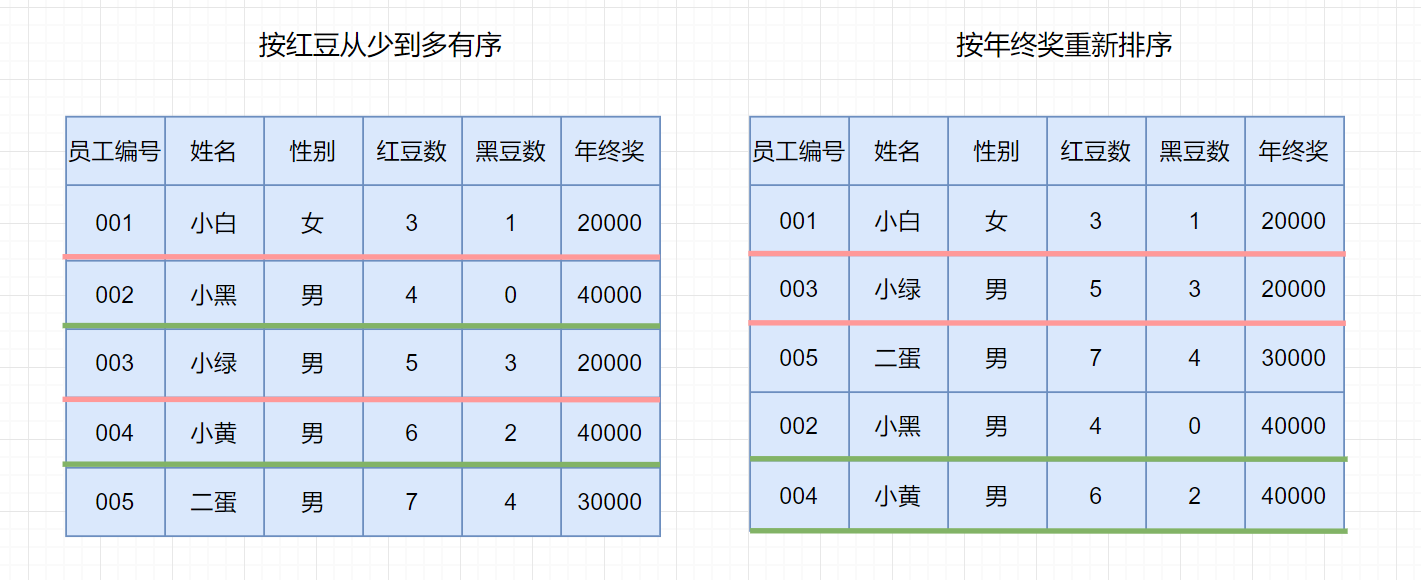
 第一次排序之后，所有的职工按照**红豆数**从少到多有序。
 
 第二次排序中，我们使用**稳定的排序算法**，所以经过第二次排序之后，年终奖相同的职工，仍然保持着红豆的有序（想对位置不变），红豆仍是从小到大排序。我们使用稳定的排序算法，只需要两次排序即可。
@@ -94,7 +92,7 @@ class Solution {
             }
         }
         return nums;
-         
+
     }
     public void swap(int[] nums,int i,int j) {
         int temp = nums[i];
@@ -142,7 +140,7 @@ class Solution {
                 }
             }
         }
-        return nums;       
+        return nums;
     }
     public void swap(int[] nums,int i,int j) {
         int temp = nums[i];
@@ -182,10 +180,10 @@ class Solution {
                     //发生交换，则变为true,下次继续判断
                     flag = true;
                 }
-            }          
+            }
         }
         return nums;
-         
+
     }
     public void swap(int[] nums,int i,int j) {
         int temp = nums[i];
@@ -227,9 +225,9 @@ class Solution:
 
 最好情况，就是要排序的表完全有序的情况下，根据改进后的代码，我们只需要一次遍历即可，
 
-只需 n -1 次比较，时间复杂度为 O(n)。最坏情况时，即待排序表逆序的情况，则需要比较(n-1) + (n-2) +.... + 2 + 1= n*(n-1)/2 ，并等量级的交换，则时间复杂度为O(n^2)。*
+只需 n -1 次比较，时间复杂度为 O(n)。最坏情况时，即待排序表逆序的情况，则需要比较(n-1) + (n-2) +.... + 2 + 1= n*(n-1)/2 ，并等量级的交换，则时间复杂度为 O(n^2)。*
 
-*平均情况下，需要 n*(n-1)/4 次交换操作，比较操作大于等于交换操作，而复杂度的上限是 O(n^2)，所以平均情况下的时间复杂度就是 O(n^2)。
+_平均情况下，需要 n_(n-1)/4 次交换操作，比较操作大于等于交换操作，而复杂度的上限是 O(n^2)，所以平均情况下的时间复杂度就是 O(n^2)。
 
 **冒泡排序空间复杂度分析**
 
@@ -239,9 +237,6 @@ class Solution:
 
 那么冒泡排序是稳定的吗？当然是稳定的，我们代码中，当 nums[j] > nums[j + 1] 时，才会进行交换，相等时不会交换，相等元素的相对位置没有改变，所以冒泡排序是稳定的。
 
-
-
 | 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
 | -------- | -------------- | -------------- | -------------- | ---------- | -------- |
 | 冒泡排序 | O(n)           | O(n^2)         | O(n^2)         | O(1)       | 稳定     |
-