mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2025-08-15 18:51:38 +00:00
代码重构 【Github Actions】
This commit is contained in:
@@ -1,8 +1,8 @@
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
>
|
||||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||||
>
|
||||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||||
|
||||
> 为保证代码严谨性,文中所有代码均在 leetcode 刷题网站 AC ,大家可以放心食用。
|
||||
|
||||
@@ -24,21 +24,17 @@
|
||||
|
||||
通过上面的一个例子,让我们简单了解了字符串匹配。
|
||||
|
||||
字符串匹配:设 S 和 T 是给定的两个串,在主串 S 中找到模式串 T 的过程称为字符串匹配,如果在主串 S 中找到 模式串 T ,则称匹配成功,函数返回 T 在 S 中首次出现的位置,否则匹配不成功,返回 -1。
|
||||
字符串匹配:设 S 和 T 是给定的两个串,在主串 S 中找到模式串 T 的过程称为字符串匹配,如果在主串 S 中找到 模式串 T ,则称匹配成功,函数返回 T 在 S 中首次出现的位置,否则匹配不成功,返回 -1。
|
||||
|
||||
例:
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
在上图中,我们试图找到模式 T = baab,在主串 S = abcabaabcabac 中第一次出现的位置,即为红色阴影部分, T 第一次在 S 中出现的位置下标为 4 ( 字符串的首位下标是 0 ),所以返回 4。如果模式串 T 没有在主串 S 中出现,则返回 -1。
|
||||
|
||||
解决上面问题的算法我们称之为字符串匹配算法,今天我们来介绍三种字符串匹配算法,大家记得打卡呀,说不准面试的时候就问到啦。
|
||||
|
||||
## BF算法(Brute Force)
|
||||
## BF 算法(Brute Force)
|
||||
|
||||
这个算法很容易理解,就是我们将模式串和主串进行比较,一致时则继续比较下一字符,直到比较完整个模式串。不一致时则将模式串后移一位,重新从模式串的首位开始对比,重复刚才的步骤下面我们看下这个方法的动图解析,看完肯定一下就能搞懂啦。
|
||||
|
||||
@@ -52,7 +48,7 @@
|
||||
|
||||
#### 题目描述
|
||||
|
||||
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
|
||||
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从 0 开始)。如果不存在,则返回 -1。
|
||||
|
||||
示例 1:
|
||||
|
||||
@@ -76,7 +72,7 @@ Java Code:
|
||||
class Solution {
|
||||
public int strStr(String haystack, String needle) {
|
||||
int haylen = haystack.length();
|
||||
int needlen = needle.length();
|
||||
int needlen = needle.length();
|
||||
//特殊情况
|
||||
if (haylen < needlen) {
|
||||
return -1;
|
||||
@@ -97,7 +93,7 @@ class Solution {
|
||||
//匹配成功
|
||||
if (j == needlen) {
|
||||
return i;
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
return -1;
|
||||
@@ -132,7 +128,7 @@ class Solution:
|
||||
return -1
|
||||
```
|
||||
|
||||
我们看一下BF算法的另一种算法(显示回退),其实原理一样,就是对代码进行了一下修改,只要是看完咱们的动图,这个也能够一下就能看懂,大家可以结合下面代码中的注释和动图进行理解。
|
||||
我们看一下 BF 算法的另一种算法(显示回退),其实原理一样,就是对代码进行了一下修改,只要是看完咱们的动图,这个也能够一下就能看懂,大家可以结合下面代码中的注释和动图进行理解。
|
||||
|
||||
Java Code:
|
||||
|
||||
@@ -165,7 +161,7 @@ class Solution {
|
||||
|
||||
Python Code:
|
||||
|
||||
```python
|
||||
```python
|
||||
from typing import List
|
||||
class Solution:
|
||||
def strStr(self, haystack: str, needle: str)->int:
|
||||
@@ -190,14 +186,11 @@ class Solution:
|
||||
return renum
|
||||
```
|
||||
|
||||
|
||||
## BM算法(Boyer-Moore)
|
||||
## BM 算法(Boyer-Moore)
|
||||
|
||||
我们刚才说过了 BF 算法,但是 BF 算法是有缺陷的,比如我们下面这种情况
|
||||
|
||||

|
||||
|
||||
|
||||

|
||||
|
||||
如上图所示,如果我们利用 BF 算法,遇到不匹配字符时,每次右移一位模式串,再重新从头进行匹配,我们观察一下,我们的模式串 abcdex 中每个字符都不一样,但是我们第一次进行字符串匹配时,abcde 都匹配成功,到 x 时失败,又因为模式串每位都不相同,所以我们不需要再每次右移一位,再重新比较,我们可以直接跳过某些步骤。如下图
|
||||
|
||||
@@ -211,7 +204,7 @@ class Solution:
|
||||
|
||||
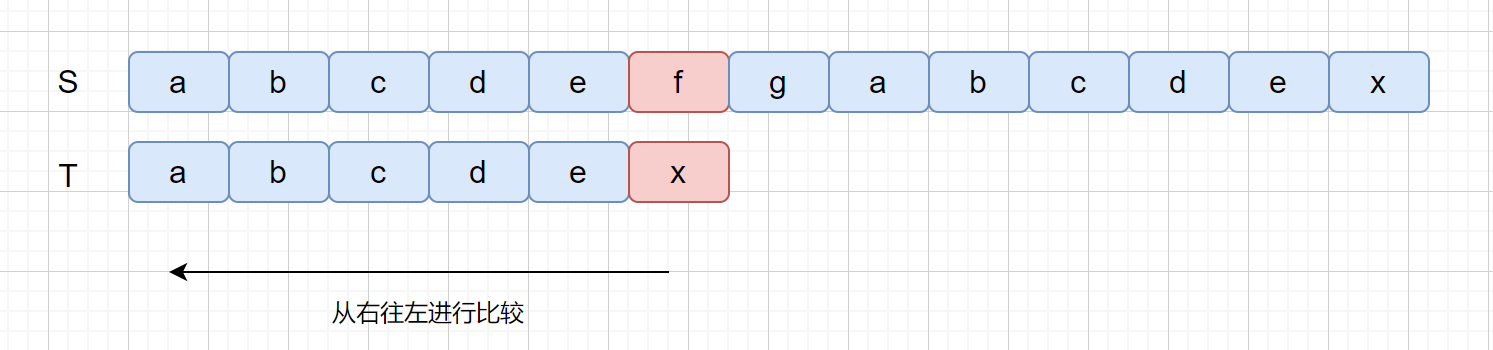
我们之前的 BF 算法是从前往后进行比较 ,BM 算法是从后往前进行比较,我们来看一下具体过程,我们还是利用上面的例子。
|
||||
|
||||
|
||||

|
||||
|
||||
BM 算法是从后往前进行比较,此时我们发现比较的第一个字符就不匹配,我们将**主串**这个字符称之为**坏字符**,也就是 f ,我们发现坏字符之后,模式串 T 中查找是否含有该字符(f),我们发现并不存在 f,此时我们只需将模式串右移到坏字符的后面一位即可。如下图
|
||||
|
||||
@@ -243,16 +236,10 @@ BM 算法是从后往前进行比较,此时我们发现比较的第一个字
|
||||
|
||||
我们上面一共介绍了三种移动情况,分别是下方的模式串中没有发现与坏字符对应的字符,发现一个对应字符,发现两个。这三种情况我们分别移动不同的位数,那我们是根据依据什么来决定移动位数的呢?下面我们给图中的字符加上下标。见下图
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
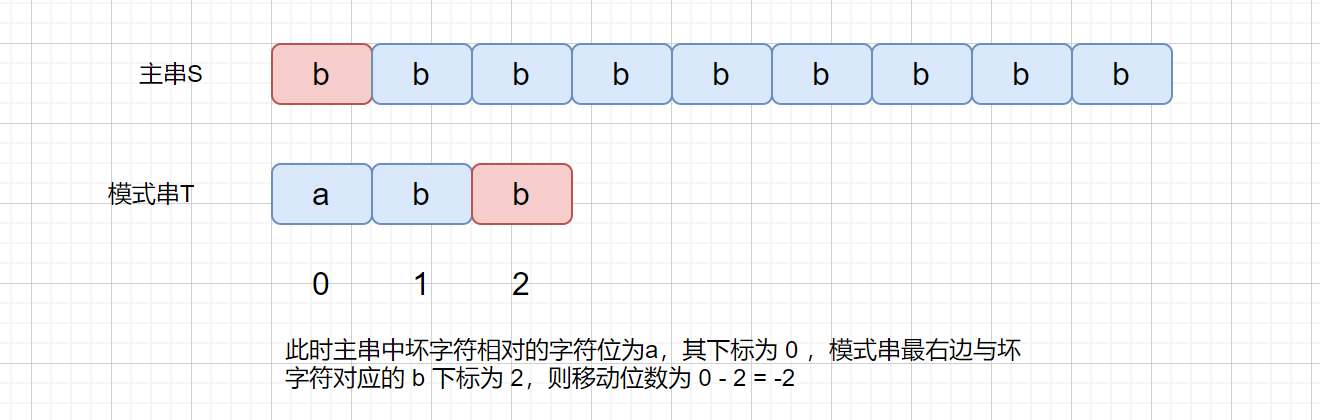
下面我们来考虑一下这种情况。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
此时这种情况肯定是不行的,不往右移动,甚至还有可能左移,那么我们有没有什么办法解决这个问题呢?继续往下看吧。
|
||||
@@ -265,7 +252,7 @@ BM 算法是从后往前进行比较,此时我们发现比较的第一个字
|
||||
|
||||
这里如果我们按照坏字符进行移动是不合理的,这时我们可以使用好后缀规则,那么什么是好后缀呢?
|
||||
|
||||
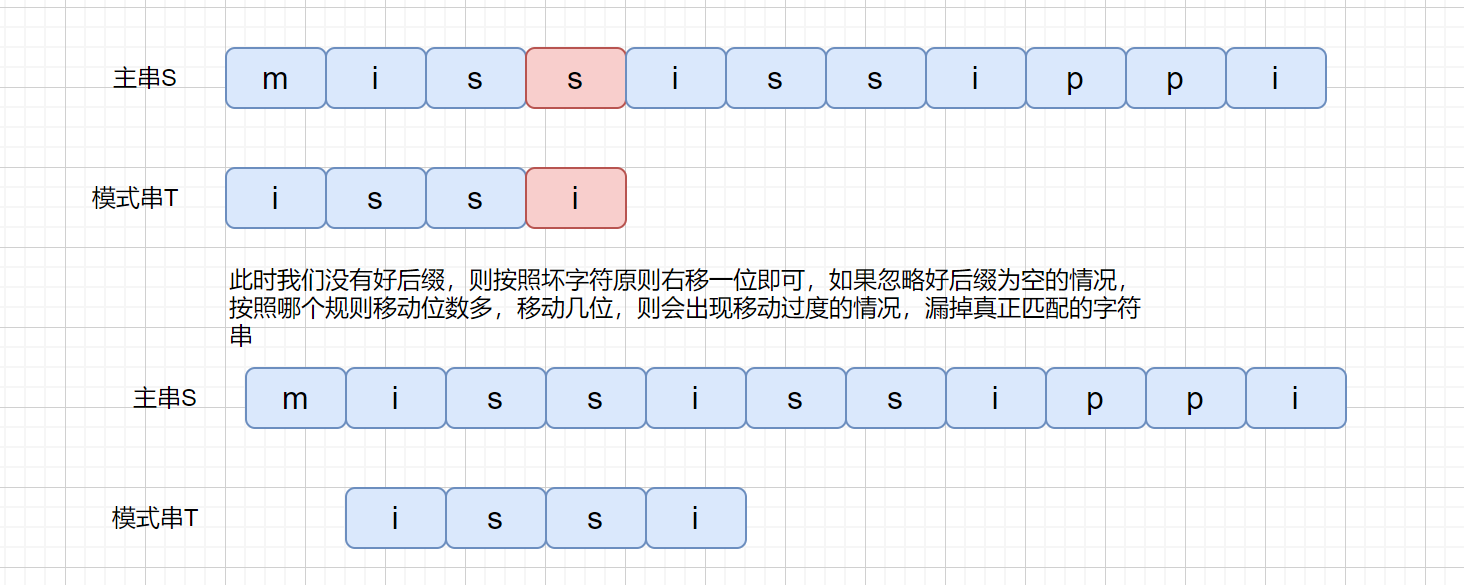
BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已经匹配成功,在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀,此时我们拿它在模式串中查找,如果找到了另一个和好后缀相匹配的串,那我们就将另一个和**好后缀相匹配**的串 ,滑到和好后缀对齐的位置。
|
||||
BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已经匹配成功,在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀,此时我们拿它在模式串中查找,如果找到了另一个和好后缀相匹配的串,那我们就将另一个和**好后缀相匹配**的串 ,滑到和好后缀对齐的位置。
|
||||
|
||||
是不是感觉有点拗口,没关系,我们看下图,红色代表坏字符,绿色代表好后缀
|
||||
|
||||
@@ -289,16 +276,8 @@ BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已
|
||||
|
||||
下面我们通过动图来看一下某一例子的具体的执行过程
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
视频
|
||||
|
||||
|
||||
|
||||
说到这里,坏字符和好后缀规则就算说完了,坏字符很容易理解,我们对好后缀总结一下
|
||||
|
||||
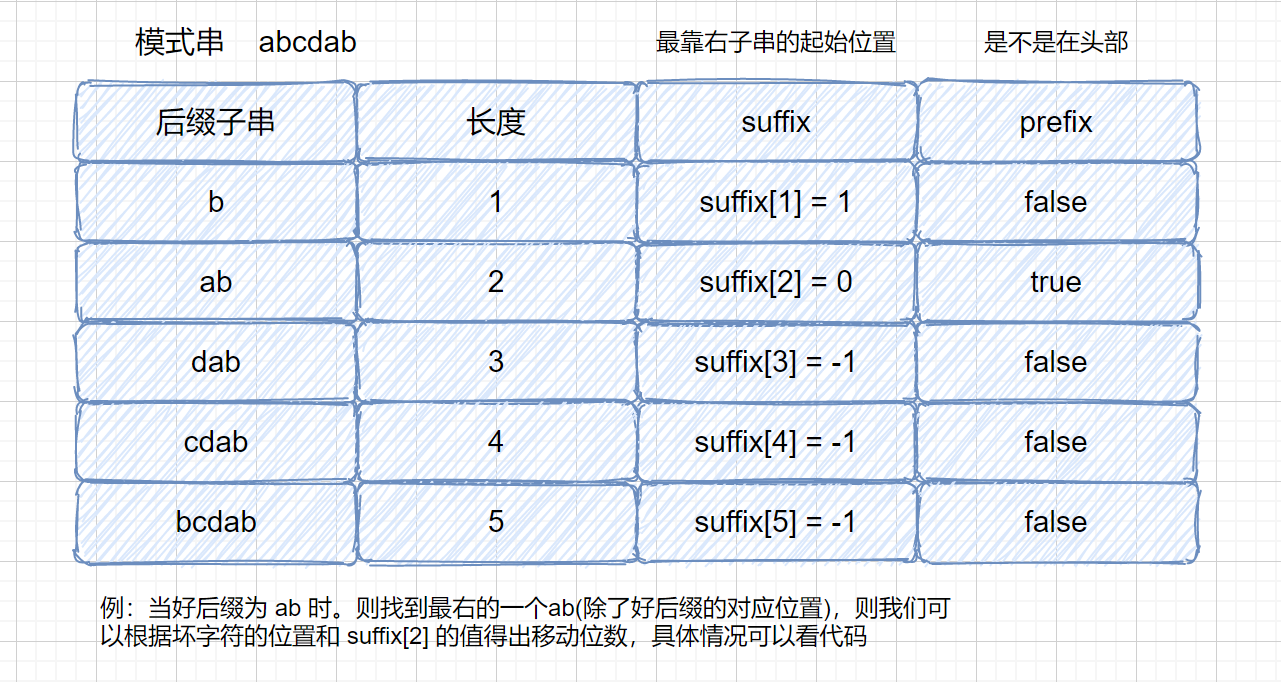
1.如果模式串**含有好后缀**,无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次,则以**最右侧的好后缀**为基准。
|
||||
@@ -309,8 +288,6 @@ BM 算法是从右往左进行比较,发现坏字符的时候此时 cac 已
|
||||
|
||||
> Boyer R S,Moore J S. A fast string searching algorithm[J]. Communications of the ACM,1977,10: 762-772.
|
||||
|
||||
|
||||
|
||||
之前我们刚开始说坏字符的时候,是不是有可能会出现负值的情况,即往左移动的情况,所以我们为了解决这个问题,我们可以分别计算好后缀和坏字符往后滑动的位数**(好后缀不为 0 的情况)**,然后取两个数中最大的,作为模式串往后滑动的位数。
|
||||
|
||||
|
||||
@@ -421,7 +398,7 @@ class Solution:
|
||||
haylen = len(haystack)
|
||||
needlen = len(needle)
|
||||
return self.bm(haystack, haylen, needle, needlen)
|
||||
|
||||
|
||||
# 用来求坏字符情况下移动位数
|
||||
def badChar(self, b: str, m: int, bc: List[int]):
|
||||
# 初始化
|
||||
@@ -431,7 +408,7 @@ class Solution:
|
||||
for i in range(0, m,):
|
||||
ascii = ord(b[i])
|
||||
bc[ascii] = i# 下标
|
||||
|
||||
|
||||
# 用来求好后缀条件下的移动位数
|
||||
def goodSuffix(self, b: str, m: int, suffix: List[int], prefix: List[bool]):
|
||||
# 初始化
|
||||
@@ -447,7 +424,7 @@ class Solution:
|
||||
suffix[k] = j + 1
|
||||
if j == -1:
|
||||
prefix[k] = True
|
||||
|
||||
|
||||
def bm(self, a: str, n: int, b: str, m: int)->int:
|
||||
bc = [0] * 256# 创建一个数组用来保存最右边字符的下标
|
||||
self.badChar(b, m, bc)
|
||||
@@ -478,7 +455,7 @@ class Solution:
|
||||
# 移动
|
||||
i += max(x, y)
|
||||
return -1
|
||||
|
||||
|
||||
# j代表坏字符的下标
|
||||
def move(j: int, m: int, suffix_index: List[int], ispre: List[bool])->int:
|
||||
# 好后缀长度
|
||||
@@ -499,7 +476,7 @@ class Solution:
|
||||
|
||||
|
||||
|
||||
## KMP算法(Knuth-Morris-Pratt)
|
||||
## KMP 算法(Knuth-Morris-Pratt)
|
||||
|
||||
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
|
||||
|
||||
@@ -507,12 +484,6 @@ class Solution:
|
||||
|
||||
视频
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
|
||||
|
||||
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
|
||||
@@ -531,7 +502,7 @@ class Solution:
|
||||
|
||||

|
||||
|
||||
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
||||
好啦,看完上面的图,KMP 的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
|
||||
|
||||
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
|
||||
|
||||
@@ -644,7 +615,7 @@ class Solution:
|
||||
nelen = len(needle)
|
||||
# 返回下标
|
||||
return self.kmp(haystack, halen, needle, nelen)
|
||||
|
||||
|
||||
def kmp(self, hasyarr: str, halen: int, nearr: str, nelen: int)->int:
|
||||
# 获取next 数组
|
||||
next = self.next(nearr, nelen)
|
||||
@@ -688,4 +659,3 @@ class Solution:
|
||||
```
|
||||
|
||||
这篇文章真的写了很久很久,觉得还不错的话,就麻烦您点个赞吧,大家也可以去我的公众号看我的所有文章,每个都有动图解析,公众号:[袁厨的算法小屋](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/qrcode_for_gh_1f36d2ef6df9_258.5lojyphpkso0.jpg)
|
||||
|
||||
|
||||
Reference in New Issue
Block a user