mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2026-03-13 05:11:08 +00:00
代码重构 【Github Actions】
This commit is contained in:
@@ -1,8 +1,8 @@
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
>
|
||||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||||
>
|
||||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||||
|
||||
#### [剑指 offer 51 数组中的逆序对](https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof)
|
||||
|
||||
@@ -10,13 +10,13 @@
|
||||
|
||||
|
||||
|
||||
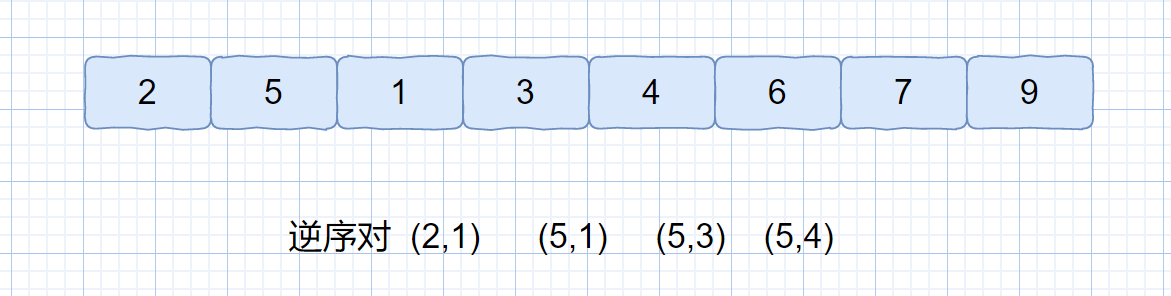
是不是很容易理解,因为数组是无序的,当较大的数,出现在较小数前面的时候,它俩则可以组成逆序对。因为数组的(有序度+逆序度)= n (n-1) / 2,逆序对个数 = 数组的逆序度,有序对个数 = 数组的有序度,所以我们知道有序对个数的话,也能得到逆序对的个数。另外我们如何通过归并排序来计算逆序对个数呢?
|
||||
是不是很容易理解,因为数组是无序的,当较大的数,出现在较小数前面的时候,它俩则可以组成逆序对。因为数组的(有序度+逆序度)= n (n-1) / 2,逆序对个数 = 数组的逆序度,有序对个数 = 数组的有序度,所以我们知道有序对个数的话,也能得到逆序对的个数。另外我们如何通过归并排序来计算逆序对个数呢?
|
||||
|
||||
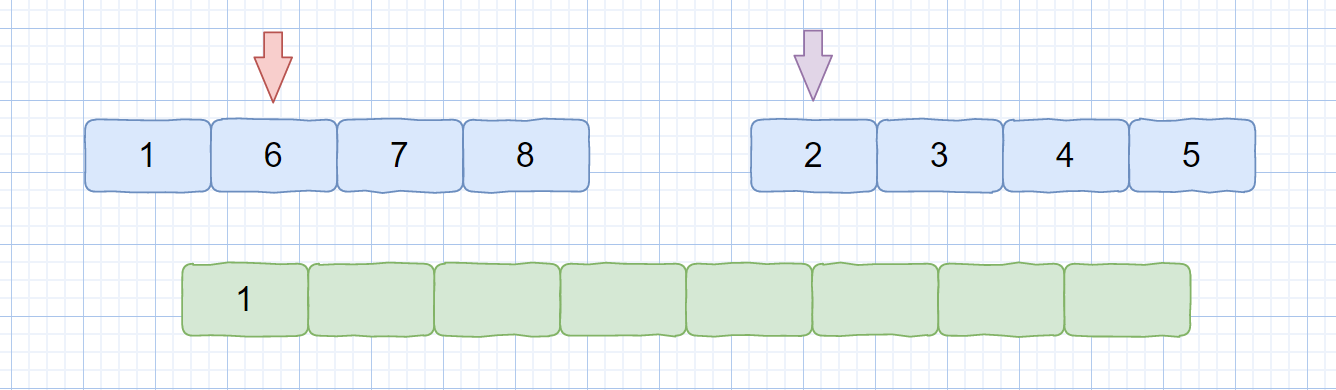
关键点在我们的**归并过程中**,我们先来看下归并过程中是怎么计算逆序对个数的。见下图
|
||||
|
||||
|
||||
|
||||
我们来拆解下上图,我们此时 temp1 指向元素为 6,temp2 指向元素为 2, nums[temp1] > temp[temp2],则此时我们需要将 temp2 指向的元素存入临时数组中,又因为每个小集合中的元素都是有序的,所以 temp1 后面的元素也一定大于 2,那么我们就可以根据 temp1 的索引得出逆序对中包含 2 的逆序对个数,则是 mid - temp + 1。
|
||||
我们来拆解下上图,我们此时 temp1 指向元素为 6,temp2 指向元素为 2, nums[temp1] > temp[temp2],则此时我们需要将 temp2 指向的元素存入临时数组中,又因为每个小集合中的元素都是有序的,所以 temp1 后面的元素也一定大于 2,那么我们就可以根据 temp1 的索引得出逆序对中包含 2 的逆序对个数,则是 mid - temp + 1。
|
||||
|
||||
好啦这个题目你已经会做啦,下面我们一起来做下吧。
|
||||
|
||||
@@ -31,7 +31,7 @@
|
||||
|
||||
**题目解析**
|
||||
|
||||
各位如果忘记归并排序的话,可以再看一下咱们之前的文章回顾一下 [归并排序详解](https://mp.weixin.qq.com/s/YK43J73UNFRjX4r0vh13ZA),这个题目我们仅仅在归并排序的基础上加了一行代码。那就是在归并过程时,nums[temp2] < nums[temp1] 时统计个数。下面我们直接看代码吧。
|
||||
各位如果忘记归并排序的话,可以再看一下咱们之前的文章回顾一下 [归并排序详解](https://mp.weixin.qq.com/s/YK43J73UNFRjX4r0vh13ZA),这个题目我们仅仅在归并排序的基础上加了一行代码。那就是在归并过程时,nums[temp2] < nums[temp1] 时统计个数。下面我们直接看代码吧。
|
||||
|
||||
**题目代码**
|
||||
|
||||
@@ -40,9 +40,9 @@ Java Code:
|
||||
```java
|
||||
class Solution {
|
||||
//全局变量
|
||||
private int count;
|
||||
private int count;
|
||||
public int reversePairs(int[] nums) {
|
||||
count = 0;
|
||||
count = 0;
|
||||
merge(nums,0,nums.length-1);
|
||||
return count;
|
||||
}
|
||||
@@ -65,7 +65,7 @@ class Solution {
|
||||
int temp1 = left, temp2 = mid+1;
|
||||
|
||||
while (temp1 <= mid && temp2 <= right) {
|
||||
|
||||
|
||||
if (nums[temp1] <= nums[temp2]) {
|
||||
temparr[index++] = nums[temp1++];
|
||||
} else {
|
||||
@@ -74,7 +74,7 @@ class Solution {
|
||||
temparr[index++] = nums[temp2++];
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
if (temp1 <= mid) System.arraycopy(nums,temp1,temparr,index,mid-temp1+1);
|
||||
if (temp2 <= right) System.arraycopy(nums,temp2,temparr,index,right-temp2+1);
|
||||
System.arraycopy(temparr,0,nums,left,right-left+1);
|
||||
@@ -98,8 +98,8 @@ class Solution:
|
||||
mid = left + ((right - left) >> 1)
|
||||
self.mergeSort(arr, left, mid)
|
||||
self.mergeSort(arr, mid + 1, right)
|
||||
self.merge(arr, left, mid, right)
|
||||
|
||||
self.merge(arr, left, mid, right)
|
||||
|
||||
# 归并
|
||||
def merge(self, arr: List[int], left: int, mid: int, right: int):
|
||||
# 第一步,定义一个新的临时数组
|
||||
@@ -121,20 +121,15 @@ class Solution:
|
||||
# 对应第三步,将某一集合的剩余元素存到大集合中
|
||||
if temp1 <= mid:
|
||||
temparr[index: index + mid - temp1 + 1] = arr[temp1: temp1 + mid - temp1 + 1]
|
||||
if temp2 <= right:
|
||||
if temp2 <= right:
|
||||
temparr[index: index + right - temp2 + 1] = arr[temp2: temp2 + right - temp2 + 1]
|
||||
|
||||
|
||||
# 将大集合的元素复制回原数组
|
||||
arr[left: left + right- left + 1] = temparr[0: right - left + 1]
|
||||
```
|
||||
|
||||
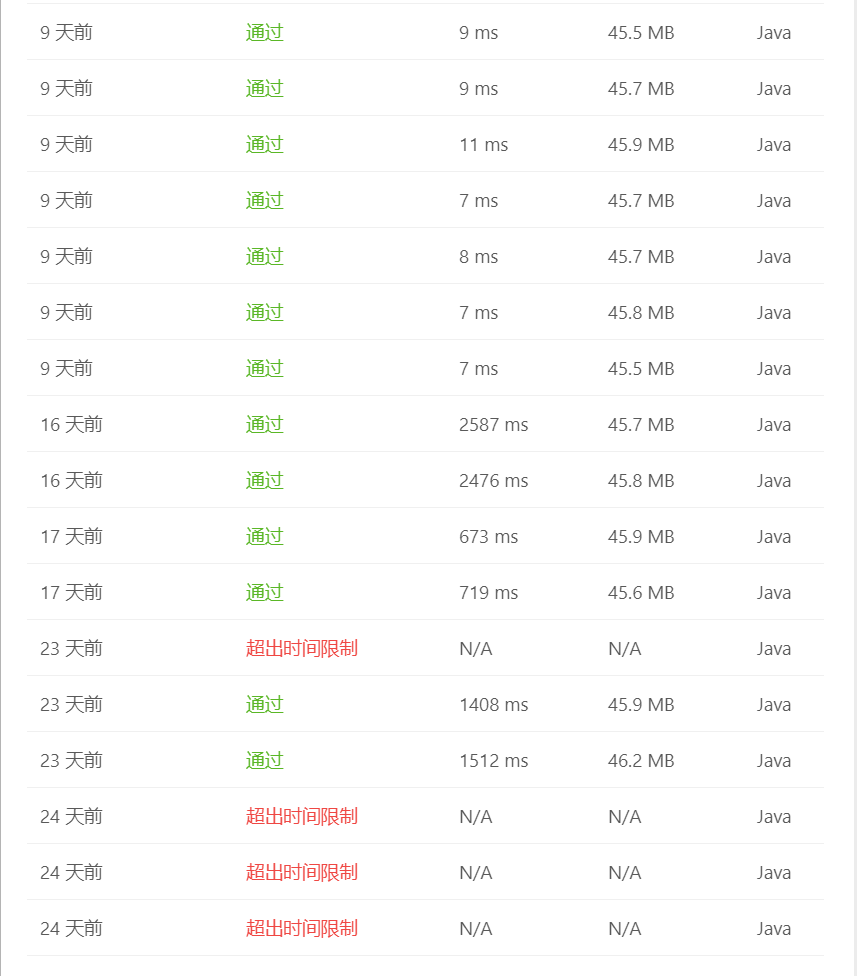
好啦,这个题目我们就解决啦,哦对,大家也可以顺手去解决下这个题目。leetcode 912 排序数组,这个题目大家可以用来练手,因为有些排序算法是面试高频考点,所以大家可以防止遗忘,多用这个题目进行练习,防止手生。下面则是我写文章时代码的提交情况,冒泡排序怎么优化都会超时,其他排序算法倒是都可以通过。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
好啦,下面我们继续做一个题目吧,也完全可以用归并排序解决,稍微加了一丢丢代码,但是也是很好理解的。感谢支持
|
||||
|
||||
|
||||
Reference in New Issue
Block a user