mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2026-03-13 13:21:21 +00:00
代码重构 【Github Actions】
This commit is contained in:
@@ -1,4 +1,4 @@
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||||
>
|
||||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||||
>
|
||||
@@ -18,8 +18,6 @@
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
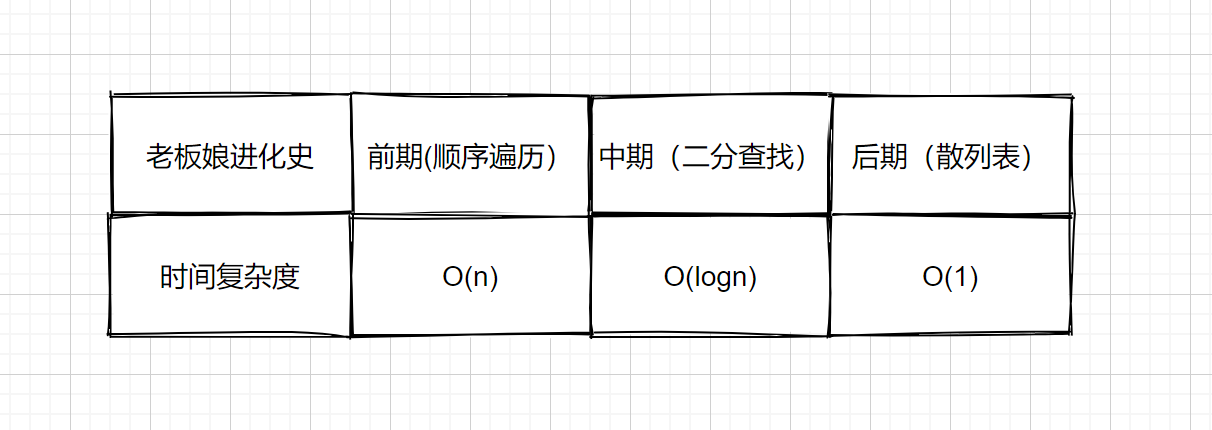
上面的后期结账的过程则模拟了我们的散列表查找,那么在计算机中是如何使用进行查找的呢?
|
||||
|
||||
### 散列表查找步骤
|
||||
@@ -36,16 +34,14 @@
|
||||
|
||||
我们假设某个函数为 **f**,使得
|
||||
|
||||
**存储位置 = f (关键字)**
|
||||
**存储位置 = f (关键字)**
|
||||
|
||||
**输入:关键字** **输出:存储位置(散列地址)**
|
||||
**输入:关键字** **输出:存储位置(散列地址)**
|
||||
|
||||
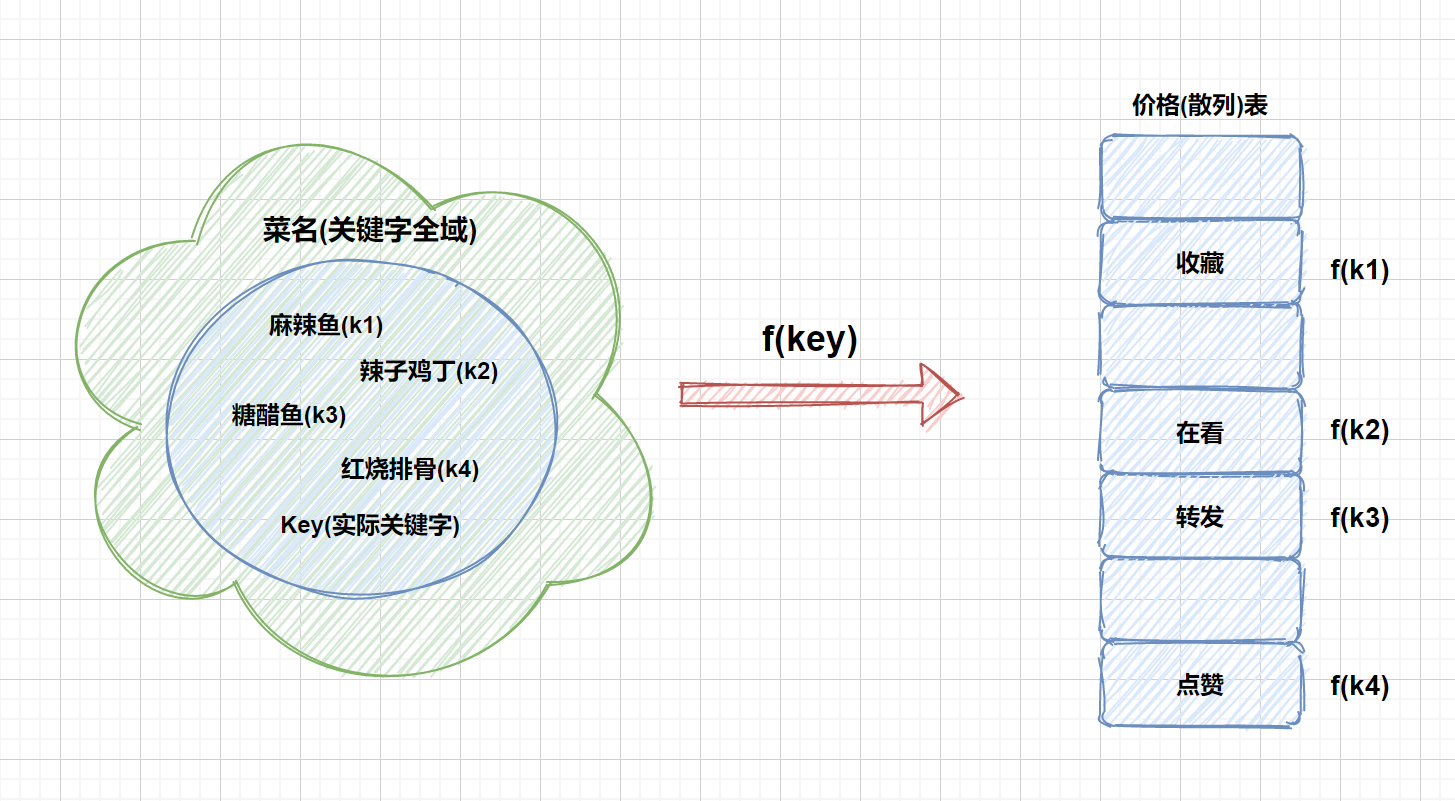
那样我们就能通过查找关键字**不需要比较**就可获得需要的记录的存储位置。这种存储技术被称为散列技术。散列技术是在通过记录的存储位置和它的关键字之间建立一个确定的对应关系 **f** ,使得每个关键字 **key** 都对应一个存储位置 **f(key)**。见下图
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
这里的 **f** 就是我们所说的散列函数(哈希)函数。我们利用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间就是我们本文的主人公------**散列(哈希)表**
|
||||
|
||||
上图为我们描述了用散列函数将关键字映射到散列表,但是大家有没有考虑到这种情况,那就是将关键字映射到同一个槽中的情况,即 **f(k4) = f(k3)** 时。这种情况我们将其称之为**冲突**,**k3** 和 **k4**则被称之为散列函数 **f** 的**同义词**,如果产生这种情况,则会让我们查找错误。幸运的是我们能找到有效的方法解决冲突。
|
||||
@@ -64,7 +60,7 @@
|
||||
|
||||
#### 直接定址法
|
||||
|
||||
如果我们对盈利为0-9的菜品设计哈希表,我们则直接可以根据作为地址,则 **f(key) = key**;
|
||||
如果我们对盈利为 0-9 的菜品设计哈希表,我们则直接可以根据作为地址,则 **f(key) = key**;
|
||||
|
||||
即下面这种情况。
|
||||
|
||||
@@ -72,9 +68,9 @@
|
||||
|
||||
有没有感觉上面的图很熟悉,没错我们经常用的数组其实就是一张哈希表,关键码就是数组的索引下标,然后我们通过下标直接访问数组中的元素。
|
||||
|
||||
另外我们假设每道菜的成本为50块,那我们还可以根据盈利+成本来作为地址,那么则 f(key) = key + 50。也就是说我们可以根据线性函数值作为散列地址。
|
||||
另外我们假设每道菜的成本为 50 块,那我们还可以根据盈利+成本来作为地址,那么则 f(key) = key + 50。也就是说我们可以根据线性函数值作为散列地址。
|
||||
|
||||
**f(key) = a * key + b** **a,b均为常数**
|
||||
**f(key) = a \* key + b** **a,b 均为常数**
|
||||
|
||||
优点:简单、均匀、无冲突。
|
||||
|
||||
@@ -94,7 +90,7 @@
|
||||
|
||||
其实这个方法也很简单,也是处理我们的关键字然后用作我们的散列地址,主要思路是将关键字从左到右分割成位数相等的几部分,然后叠加求和,并按散列表表长,取后几位作为散列地址。
|
||||
|
||||
比如我们的关键字是123456789,则我们分为三部分 123 ,456 ,789 然后将其相加得 1368 然后我们再取其后三位 368 作为我们的散列地址。
|
||||
比如我们的关键字是 123456789,则我们分为三部分 123 ,456 ,789 然后将其相加得 1368 然后我们再取其后三位 368 作为我们的散列地址。
|
||||
|
||||
优点:事先不需要知道关键字情况
|
||||
|
||||
@@ -104,26 +100,26 @@
|
||||
|
||||
在用来设计散列函数的除法散列法中,通过取 key 除以 p 的余数,将关键字映射到 p 个槽中的某一个上,对于散列表长度为 m 的散列函数公式为
|
||||
|
||||
**f(k) = k mod p (p <= m)**
|
||||
**f(k) = k mod p (p <= m)**
|
||||
|
||||
例如,如果散列表长度为 12,即 m = 12 ,我们的参数 p 也设为12,**那 k = 100时 f(k) = 100 % 12 = 4**
|
||||
例如,如果散列表长度为 12,即 m = 12 ,我们的参数 p 也设为 12,**那 k = 100 时 f(k) = 100 % 12 = 4**
|
||||
|
||||
由于只需要做一次除法操作,所以除法散列法是非常快的。
|
||||
|
||||
由上面的公式可以看出,该方法的重点在于 p 的取值,如果 p 值选的不好,就可能会容易产生同义词。见下面这种情况。我们哈希表长度为6,我们选择6为p值,则有可能产生这种情况,所有关键字都得到了0这个地址数。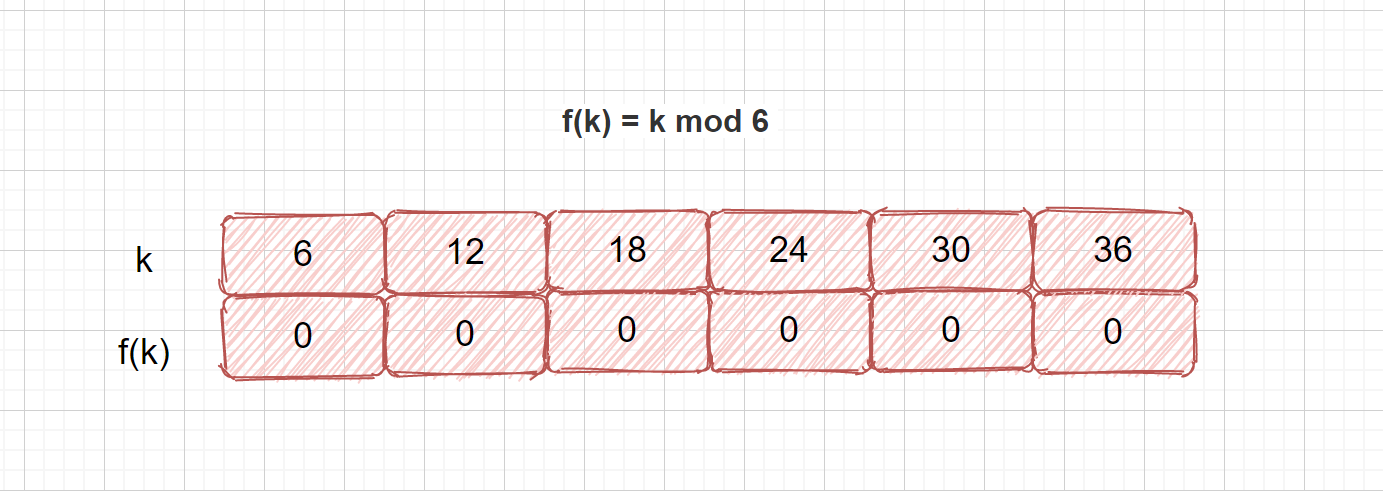
|
||||
由上面的公式可以看出,该方法的重点在于 p 的取值,如果 p 值选的不好,就可能会容易产生同义词。见下面这种情况。我们哈希表长度为 6,我们选择 6 为 p 值,则有可能产生这种情况,所有关键字都得到了 0 这个地址数。
|
||||
|
||||
那我们在选用除法散列法时选取 p 值时应该遵循怎样的规则呢?
|
||||
|
||||
- m 不应为 2 的幂,因为如果 m = 2^p ,则 f(k) 就是 k 的 p 个最低位数字。例 12 % 8 = 4 ,12的二进制表示位1100,后三位为100。
|
||||
- 若散列表长为 m ,通常 p 为 小于或等于表长(最好接近m)的最小质数或不包含小于 20 质因子的合数。
|
||||
- m 不应为 2 的幂,因为如果 m = 2^p ,则 f(k) 就是 k 的 p 个最低位数字。例 12 % 8 = 4 ,12 的二进制表示位 1100,后三位为 100。
|
||||
- 若散列表长为 m ,通常 p 为 小于或等于表长(最好接近 m)的最小质数或不包含小于 20 质因子的合数。
|
||||
|
||||
> **合数:**合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。
|
||||
> **合数:**合数是指在大于 1 的整数中除了能被 1 和本身整除外,还能被其他数(0 除外)整除的数。
|
||||
>
|
||||
> **质因子**:质因子(或质因数)在数论里是指能整除给定正整数的质数。
|
||||
|
||||
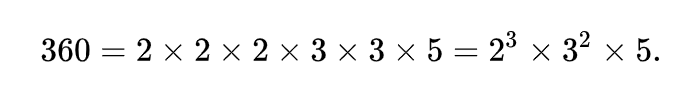
|
||||
|
||||
这里的2,3,5为质因子
|
||||
这里的 2,3,5 为质因子
|
||||
|
||||
还是上面的例子,我们根据规则选择 5 为 p 值,我们再来看。这时我们发现只有 6 和 36 冲突,相对来说就好了很多。
|
||||
|
||||
@@ -142,17 +138,17 @@
|
||||
|
||||
散列函数为
|
||||
|
||||
**f (k) = ⌊ m(kA mod 1) ⌋**
|
||||
**f (k) = ⌊ m(kA mod 1) ⌋**
|
||||
|
||||
这里的 **kA mod 1** 的含义是取 keyA 的小数部分,即 **kA - ⌊kA⌋** 。
|
||||
|
||||
优点:对 m 的选择不是特别关键,一般选择它为 2 的某个幂次(m = 2 ^ p ,p为某个整数)
|
||||
优点:对 m 的选择不是特别关键,一般选择它为 2 的某个幂次(m = 2 ^ p ,p 为某个整数)
|
||||
|
||||
应用场景:不知道关键字情况
|
||||
|
||||
#### 平方取中法
|
||||
|
||||
这个方法就比较简单了,假设关键字是 321,那么他的平方就是 103041,再抽取中间的 3 位就是 030 或 304 用作散列地址。再比如关键字是 1234 那么它的平方就是 1522756 ,抽取中间 3 位就是 227 用作散列地址.
|
||||
这个方法就比较简单了,假设关键字是 321,那么他的平方就是 103041,再抽取中间的 3 位就是 030 或 304 用作散列地址。再比如关键字是 1234 那么它的平方就是 1522756 ,抽取中间 3 位就是 227 用作散列地址.
|
||||
|
||||
优点:灵活,适用范围广泛
|
||||
|
||||
@@ -160,13 +156,13 @@
|
||||
|
||||
#### 随机数法
|
||||
|
||||
故名思意,取关键字的随机函数值为它的散列地址。也就是 **f(key) = random(key)**。这里的random是 随机函数。
|
||||
故名思意,取关键字的随机函数值为它的散列地址。也就是 **f(key) = random(key)**。这里的 random 是 随机函数。
|
||||
|
||||
优点:易实现
|
||||
|
||||
适用场景:关键字的长度不等时
|
||||
|
||||
上面我们的例子都是通过数字进行举例,那么如果是字符串可不可以作为键呢?当然也是可以的,各种各样的符号我们都可以转换成某种数字来对待,比如我们经常接触的ASCII 码,所以是同样适用的。
|
||||
上面我们的例子都是通过数字进行举例,那么如果是字符串可不可以作为键呢?当然也是可以的,各种各样的符号我们都可以转换成某种数字来对待,比如我们经常接触的 ASCII 码,所以是同样适用的。
|
||||
|
||||
以上就是常用的散列函数构造方法,其实他们的中心思想是一致的,将关键字经过加工处理之后变成另外一个数字,而这个数字就是我们的存储位置,是不是有一种间谍传递情报的感觉。
|
||||
|
||||
@@ -200,29 +196,25 @@
|
||||
|
||||
下面我们先来看一下线性探测,公式:
|
||||
|
||||
> **f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
||||
> **f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
||||
|
||||
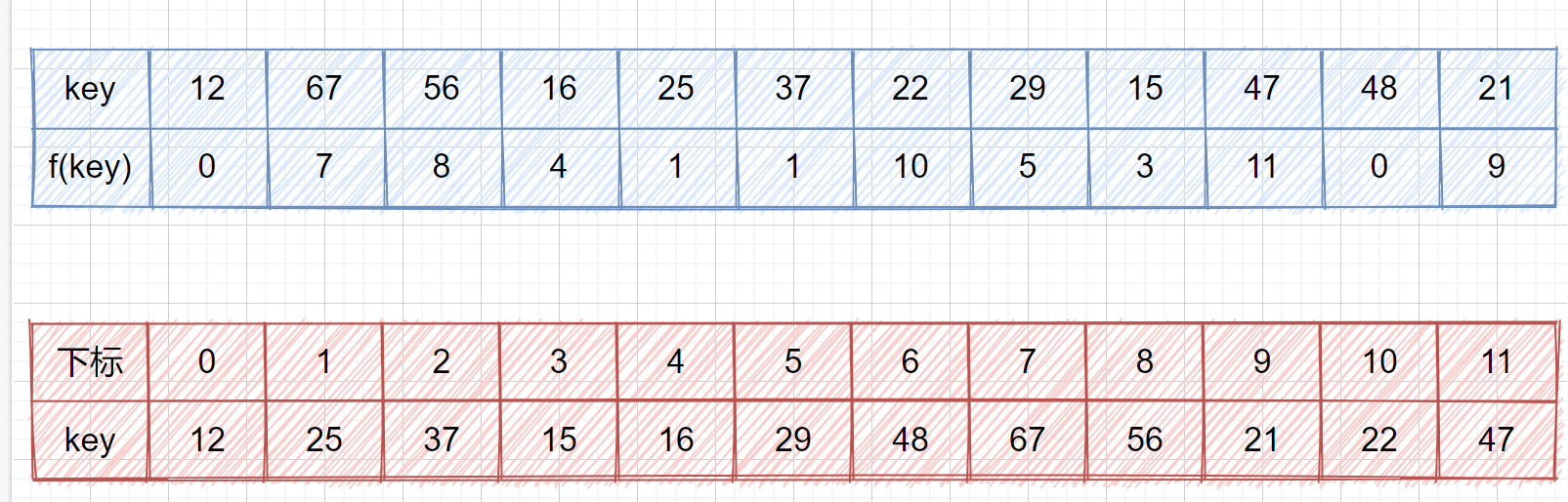
我们来看一个例子,我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为12,我们再用散列函数 **f(key) = key mod 12。**
|
||||
我们来看一个例子,我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为 12,我们再用散列函数 **f(key) = key mod 12。**
|
||||
|
||||
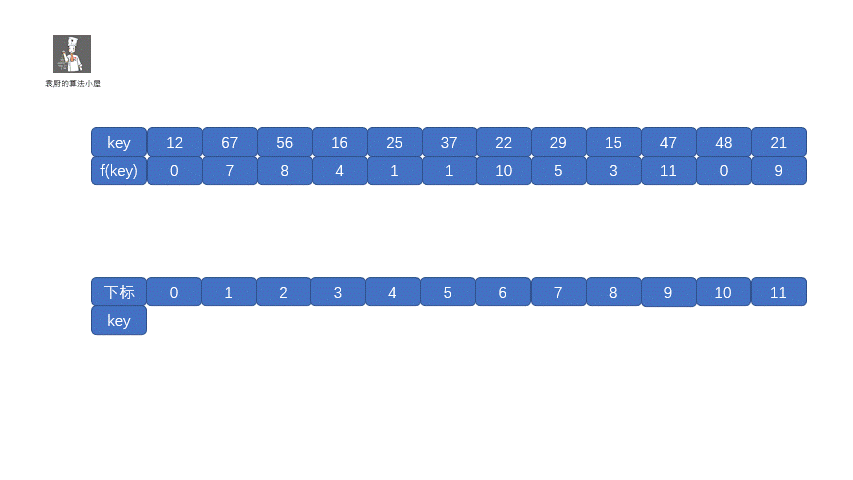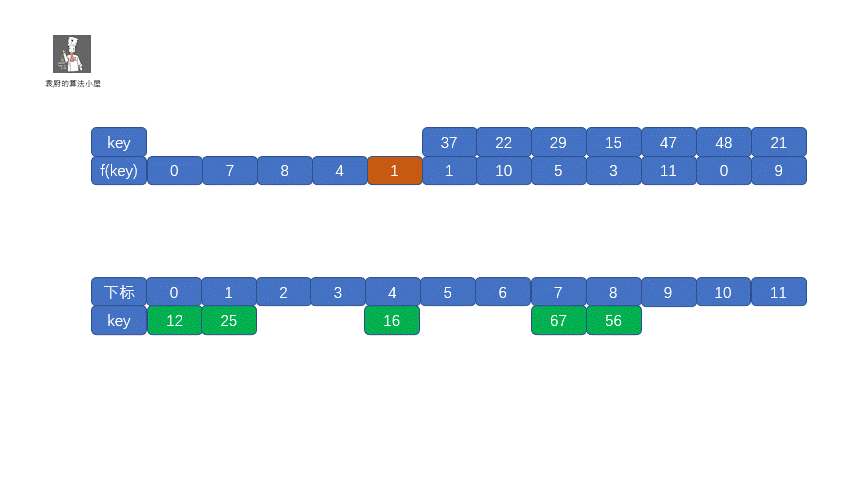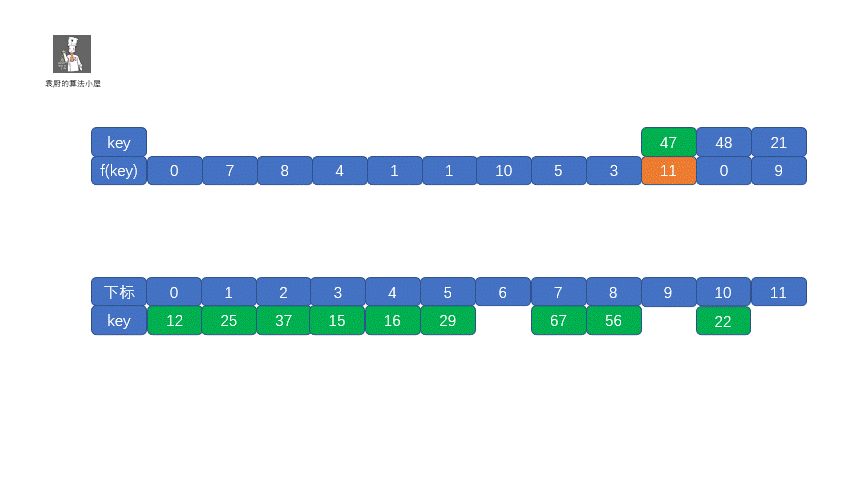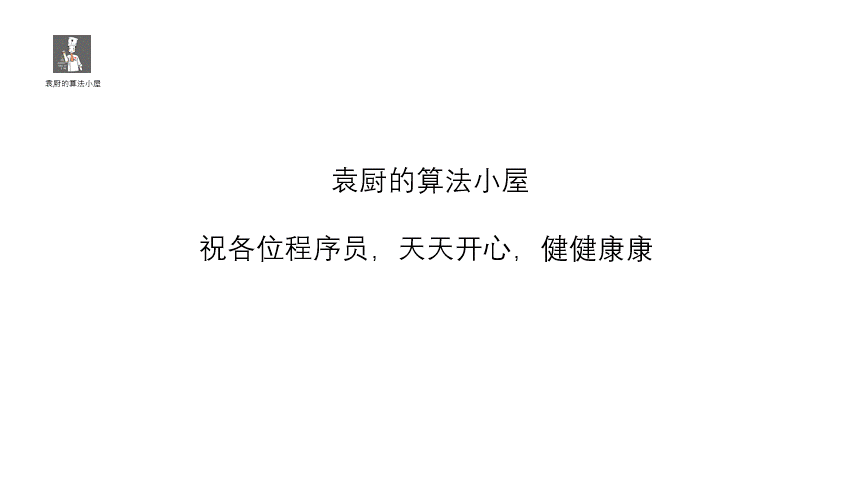
我们求出每个 key 的 f(key)见下表
|
||||
|
||||

|
||||
|
||||
我们查看上表发现,前五位的 **f(key)** 都不相同,即没有冲突,可以直接存入,但是到了第六位 **f(37) = f(25) = 1**,那我们就需要利用上面的公式 **f(37) = f (f(37) + 1 ) mod 12 = 2**,这其实就是我们的订包间的做法。下面我们看一下将上面的所有数存入哈希表是什么情况吧。
|
||||
我们查看上表发现,前五位的 **f(key)** 都不相同,即没有冲突,可以直接存入,但是到了第六位 **f(37) = f(25) = 1**,那我们就需要利用上面的公式 **f(37) = f (f(37) + 1 ) mod 12 = 2**,这其实就是我们的订包间的做法。下面我们看一下将上面的所有数存入哈希表是什么情况吧。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
我们把这种解决冲突的开放地址法称为**线性探测法**。下面我们通过视频来模拟一下线性探测法的存储过程。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
另外我们在解决冲突的时候,会遇到 48 和 37 虽然不是同义词,却争夺一个地址的情况,我们称其为**堆积**。因为堆积使得我们需要不断的处理冲突,插入和查找效率都会大大降低。
|
||||
|
||||
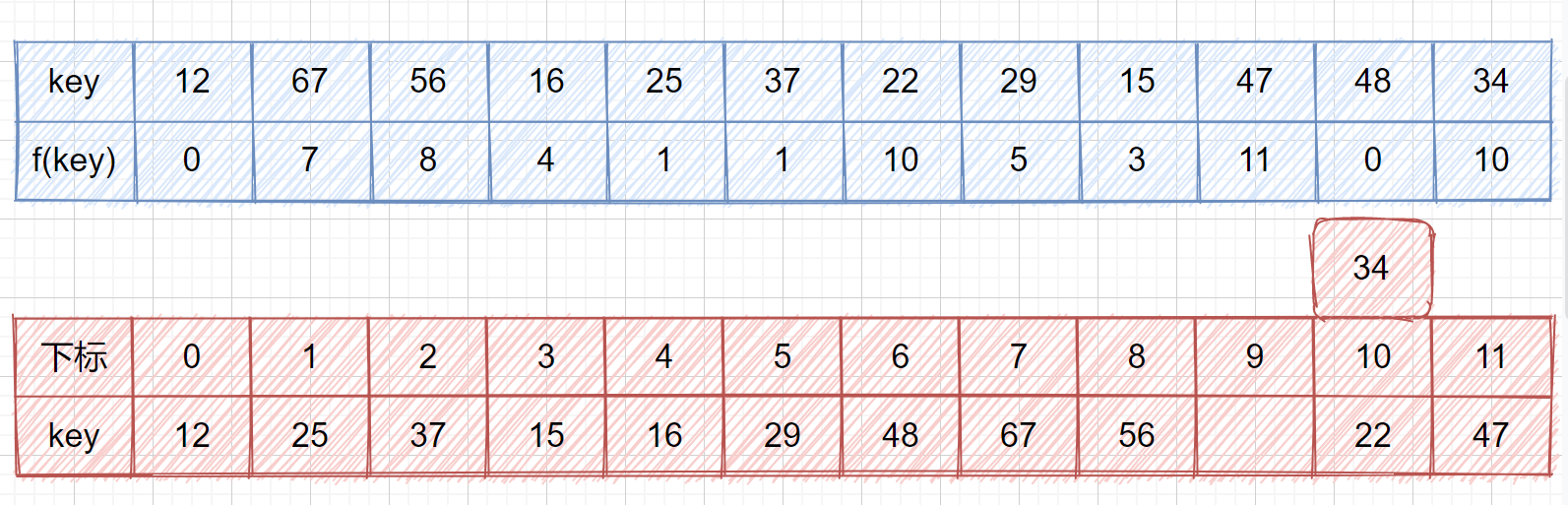
通过上面的视频我们应该了解了线性探测的执行过程了,那么我们考虑一下这种情况,若是我们的最后一位不为21,为 34 时会有什么事情发生呢?
|
||||
通过上面的视频我们应该了解了线性探测的执行过程了,那么我们考虑一下这种情况,若是我们的最后一位不为 21,为 34 时会有什么事情发生呢?
|
||||
|
||||
|
||||
|
||||
@@ -230,15 +222,15 @@
|
||||
|
||||
##### 二次探测法
|
||||
|
||||
其实理解了我们的上个例子之后,这个一下就能整明白了,根本不用费脑子,这个方法就是更改了一下di的取值
|
||||
其实理解了我们的上个例子之后,这个一下就能整明白了,根本不用费脑子,这个方法就是更改了一下 di 的取值
|
||||
|
||||
> **线性探测: f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
||||
> **线性探测: f,(key) = ( f(key) + di ) MOD m(di = 1,2,3,4,5,6....m-1)**
|
||||
>
|
||||
> **二次探测:** **f,(key) = ( f(key) + di ) MOD m(di =1^2 , -1^2 , 2^2 , -2^2 .... q^2, -q^2, q<=m/2)**
|
||||
> **二次探测:** **f,(key) = ( f(key) + di ) MOD m(di =1^2 , -1^2 , 2^2 , -2^2 .... q^2, -q^2, q<=m/2)**
|
||||
|
||||
**注:这里的是 -1^2 为负值 而不是 (-1)^2**
|
||||
**注:这里的是 -1^2 为负值 而不是 (-1)^2**
|
||||
|
||||
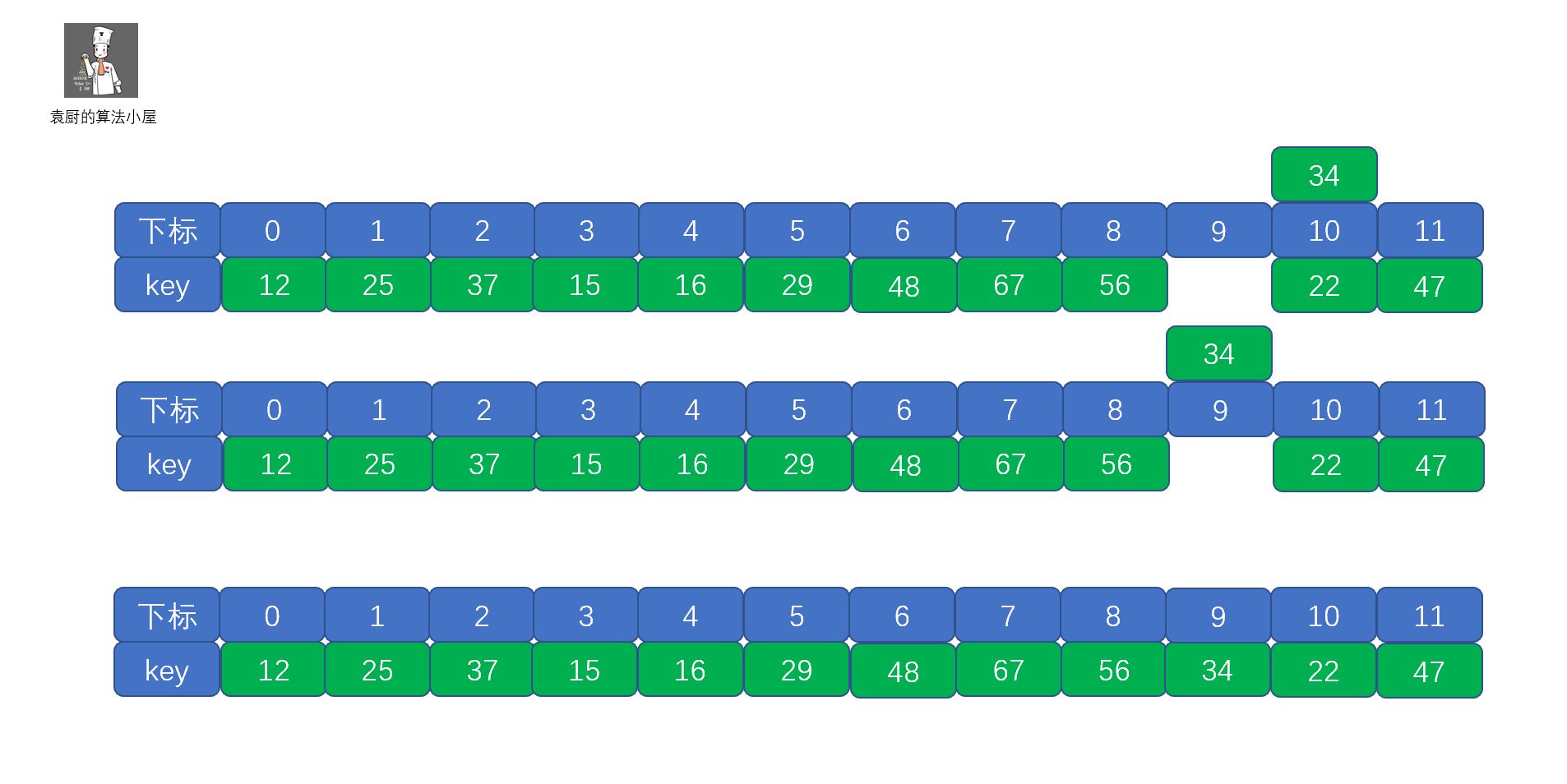
所以对于我们的34来说,当di = -1时,就可以找到空位置了。
|
||||
所以对于我们的 34 来说,当 di = -1 时,就可以找到空位置了。
|
||||
|
||||
|
||||
|
||||
@@ -266,9 +258,9 @@
|
||||
|
||||
这个方法其实也特别简单,利用不同的哈希函数再求得一个哈希地址,直到不出现冲突为止。
|
||||
|
||||
> **f,(key) = RH,( key ) (i = 1,2,3,4.....k)**
|
||||
> **f,(key) = RH,( key ) (i = 1,2,3,4.....k)**
|
||||
|
||||
这里的RH,就是不同的散列函数,你可以把我们之前说过的那些散列函数都用上,每当发生冲突时就换一个散列函数,相信总有一个能够解决冲突的。这种方法能使关键字不产生聚集,但是代价就是增加了计算时间。是不是很简单啊。
|
||||
这里的 RH,就是不同的散列函数,你可以把我们之前说过的那些散列函数都用上,每当发生冲突时就换一个散列函数,相信总有一个能够解决冲突的。这种方法能使关键字不产生聚集,但是代价就是增加了计算时间。是不是很简单啊。
|
||||
|
||||
#### 链地址法
|
||||
|
||||
@@ -286,14 +278,12 @@
|
||||
|
||||
上面我们都是遇到冲突之后,就换地方。那么我们有没有不换地方的办法呢?那就是我们现在说的链地址法。
|
||||
|
||||
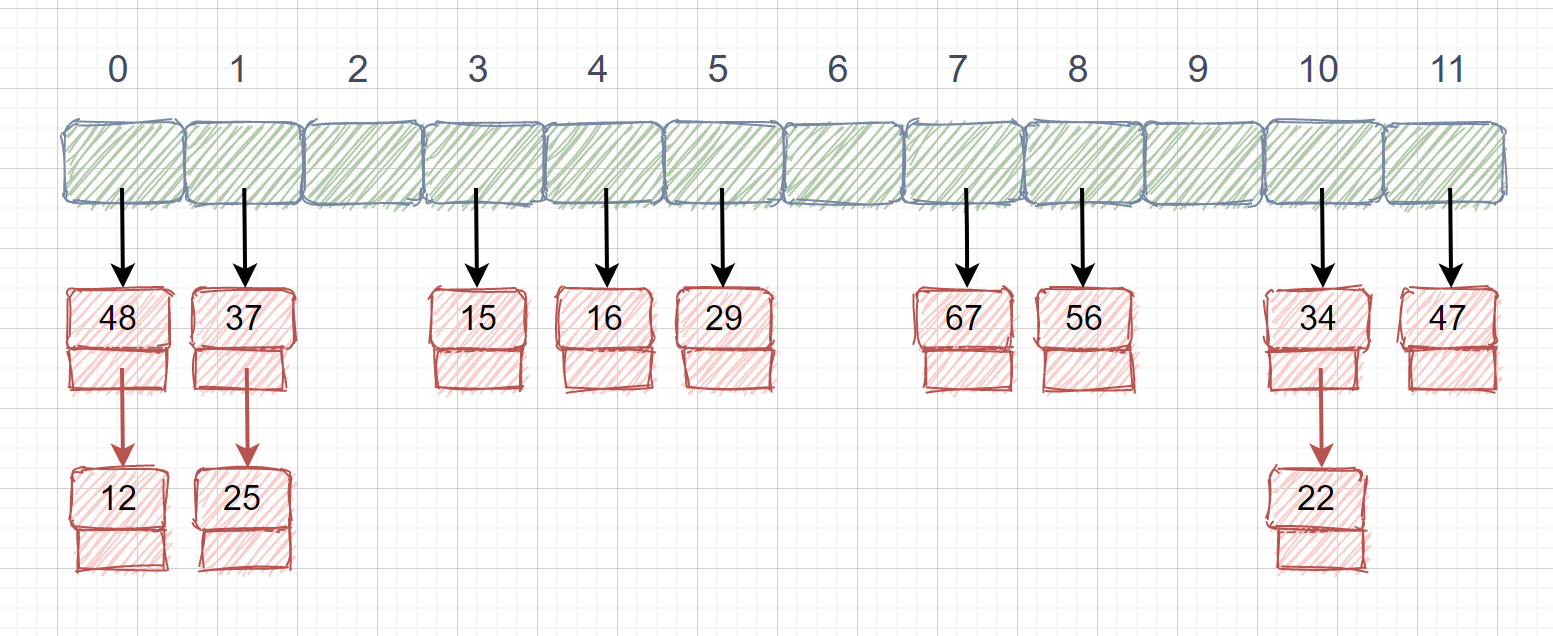
还记得我们说过得同义词吗?就是 key 不同 f(key) 相同的情况,我们将这些同义词存储在一个单链表中,这种表叫做同义词子表,散列表中只存储同义词子表的头指针。我们还是用刚才的例子,关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为12,我们再用散列函数 **f(key) = key mod 12。**我们用了链地址法之后就再也不存在冲突了,无论有多少冲突,我们只需在同义词子表中添加结点即可。下面我们看下链地址法的存储情况。
|
||||
还记得我们说过得同义词吗?就是 key 不同 f(key) 相同的情况,我们将这些同义词存储在一个单链表中,这种表叫做同义词子表,散列表中只存储同义词子表的头指针。我们还是用刚才的例子,关键字集合为{12,67,56,16,25,37,22,29,15,47,48,21},表长为 12,我们再用散列函数 **f(key) = key mod 12。**我们用了链地址法之后就再也不存在冲突了,无论有多少冲突,我们只需在同义词子表中添加结点即可。下面我们看下链地址法的存储情况。
|
||||
|
||||
|
||||
|
||||
链地址法虽然能够不产生冲突,但是也带来了查找时需要遍历单链表的性能消耗,有得必有失嘛。
|
||||
|
||||
|
||||
|
||||
#### 公共溢出区法
|
||||
|
||||
下面我们再来看一种新的方法,这回大鹏又要来吃饭了。
|
||||
@@ -318,7 +308,7 @@
|
||||
|
||||
下面我们来看一下散列表查找算法的实现
|
||||
|
||||
首先需要定义散列列表的结构以及一些相关常数,其中elem代表散列表数据存储数组,count代表的是当前插入元素个数,size代表哈希表容量,NULLKEY散列表初始值,然后我们如果查找成功就返回索引,如果不存在该元素就返回元素不存在。
|
||||
首先需要定义散列列表的结构以及一些相关常数,其中 elem 代表散列表数据存储数组,count 代表的是当前插入元素个数,size 代表哈希表容量,NULLKEY 散列表初始值,然后我们如果查找成功就返回索引,如果不存在该元素就返回元素不存在。
|
||||
|
||||
我们将哈希表初始化,为数组元素赋初值。
|
||||
|
||||
@@ -336,7 +326,7 @@
|
||||
|
||||
(1)通过哈希函数(同插入时一样),将 key 转成数组下标
|
||||
|
||||
(2)通过数组下标找到 key值,如果 key 一致,则查找成功,否则利用线性探测法继续查找。
|
||||
(2)通过数组下标找到 key 值,如果 key 一致,则查找成功,否则利用线性探测法继续查找。
|
||||
|
||||

|
||||
|
||||
@@ -346,7 +336,7 @@
|
||||
|
||||
### 散列表性能分析
|
||||
|
||||
如果没有冲突的话,散列查找是我们查找中效率最高的,时间复杂度为O(1),但是没有冲突的情况是一种理想情况,那么散列查找的平均查找长度取决于哪些方面呢?
|
||||
如果没有冲突的话,散列查找是我们查找中效率最高的,时间复杂度为 O(1),但是没有冲突的情况是一种理想情况,那么散列查找的平均查找长度取决于哪些方面呢?
|
||||
|
||||
**1.散列函数是否均匀**
|
||||
|
||||
@@ -360,8 +350,6 @@
|
||||
|
||||
本来想在上文中提到装填因子的,但是后来发现即使没有说明也不影响我们对哈希表的理解,下面我们来看一下装填因子的总结
|
||||
|
||||
> 装填因子 α = 填入表中的记录数 / 散列表长度
|
||||
|
||||
散列因子则代表着散列表的装满程度,表中记录越多,α就越大,产生冲突的概率就越大。我们上面提到的例子中 表的长度为12,填入记录数为6,那么此时的 α = 6 / 12 = 0.5 所以说当我们的 α 比较大时再填入元素那么产生冲突的可能性就非常大了。所以说散列表的平均查找长度取决于装填因子,而不是取决于记录数。所以说我们需要做的就是选择一个合适的装填因子以便将平均查找长度限定在一个范围之内。
|
||||
|
||||
> 装填因子 α = 填入表中的记录数 / 散列表长度
|
||||
|
||||
散列因子则代表着散列表的装满程度,表中记录越多,α 就越大,产生冲突的概率就越大。我们上面提到的例子中 表的长度为 12,填入记录数为 6,那么此时的 α = 6 / 12 = 0.5 所以说当我们的 α 比较大时再填入元素那么产生冲突的可能性就非常大了。所以说散列表的平均查找长度取决于装填因子,而不是取决于记录数。所以说我们需要做的就是选择一个合适的装填因子以便将平均查找长度限定在一个范围之内。
|
||||
|
||||
Reference in New Issue
Block a user