# 希望这篇文章能合你的胃口
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
>
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
>
> 另外希望手机阅读的同学可以来我的 [**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png) 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)进入。
大家在学习数据结构的时候应该都学习过栈和队列,对他俩的原理应该很熟悉了,栈是先进后出,队列是后进后出。下面我们通过这篇文章来帮助小伙伴们回忆一下栈和队列的那些事。
阅读完这篇文章你会有以下收获。
了解栈和队列的意义
了解栈和队列的实现方式
了解循环队列
学会中缀表达式转后缀表达式
学会后缀表达式的运算
## 这是栈
### 栈模型
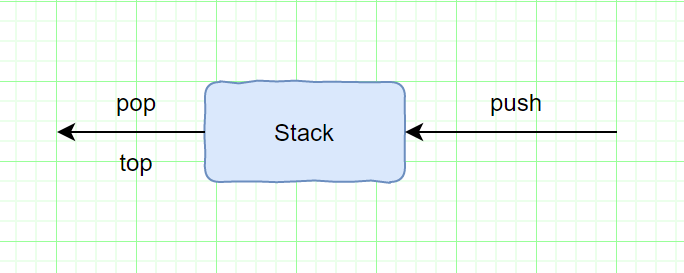
**栈(stack)是限制插入和删除只能在一个位置上进行的表**,该位置是表的末端叫做栈的顶(top),对栈的基本操作有push(进栈)和pop(出栈),前者相当于插入,后者则是删除最后插入的元素。
栈的另一个名字是LIFO(先进后出)表。普通的清空栈的操作和判断是否空栈的测试都是栈的操作指令系统的一部分,我们对栈能做的基本上也就是push和pop操作。
注:该图描述的模型只象征着push是输入操作,pop和top是输出操作
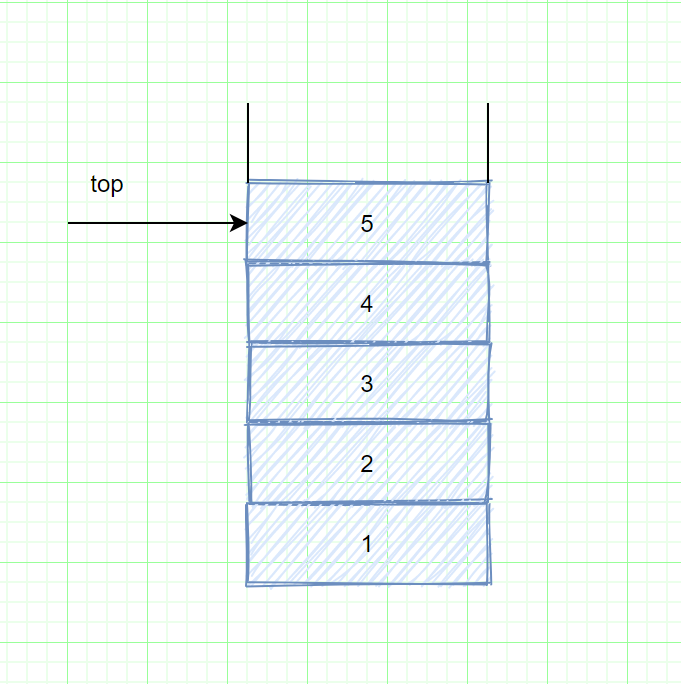
下图表示进行若干操作后的一个抽象的栈。一般的模型是,存在某个元素位于栈顶,而该元素是唯一可见元素。
### 栈的实现
因为栈是一个表,因此能够实现表的方法都可以实现栈,ArrayList和LinkedList都可以支持栈操作。
刷题时我们可以直接使用Stack类来进行创建一个栈。刷题时我们可以通过下列代码创建一个栈。下面两种方式哪种都可以使用。
```
Deque stack = new LinkedList();//类型为TreeNode
Stack stack = new Stack();
```
### 栈的应用
栈在现实中应用场景很多,大家在刷题时就可以注意到,很多题目都可以用栈来解决的。下面我们来说一个比较常用的情景,数字表达式的求值。
不知道大家是否还记得那句口令,先乘除,后加减,从左算到右,有括号的话就先算括号里面的。这是我们做小学数学所用到的。四则运算中括号也是其中的一部分,先乘除后加减使运算变的复杂,加上括号后甚之,那么我们有什么办法可以让其变的更好处理呢?波兰数学家**Jan Łukasiewicz**想到了一种不需要括号的后缀表达式,,我们也将它称之为逆波兰表示。不用数学家名字命名的原因有些尴尬,居然是因为他的名字太复杂了,所以用了国籍来表示而不是姓名。所以各位小伙伴以后给孩子起名字的时候不要太复杂啊。
> 扬·武卡谢维奇([波兰语](https://baike.baidu.com/item/波兰语):*Jan Łukasiewicz*,1878年12月21日[乌克兰](https://baike.baidu.com/item/乌克兰)利沃夫 - 1956年2月13日爱尔兰都柏林),[波兰](https://baike.baidu.com/item/波兰)数学家,主要致力于[数理逻辑](https://baike.baidu.com/item/数理逻辑)的研究。著名的波兰表示法逆波兰表示法就是他的研究成果。
#### 中缀表达式转为后缀表达式
我们通过一个例子,来说明如何将中缀表达式转为后缀表达式。
例
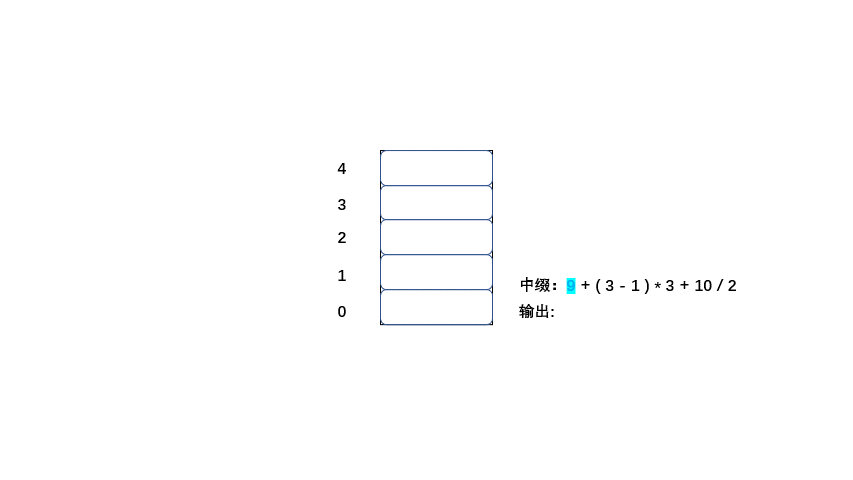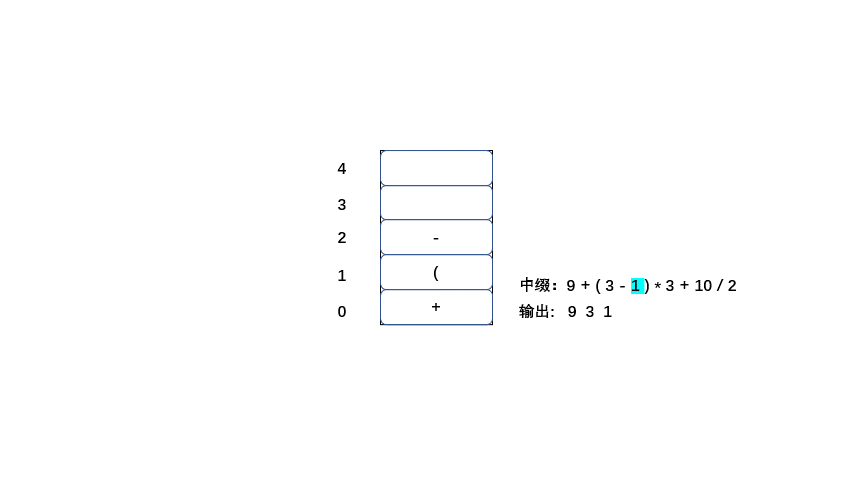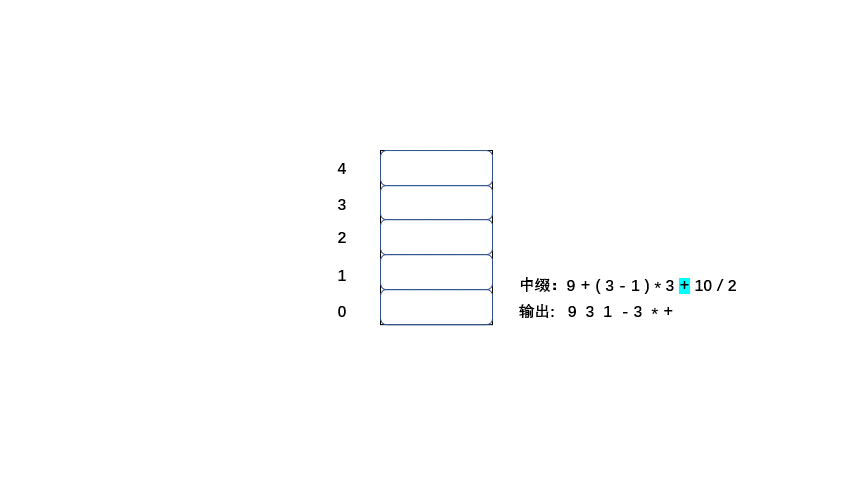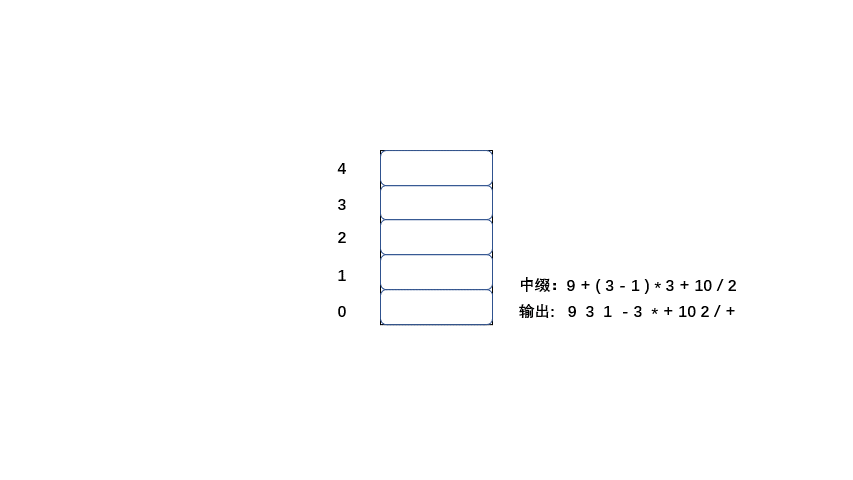
中缀:9 + ( 3 - 1 ) * 3 + 10 / 2
后缀:9 3 1 - 3 * + 10 2 / +
规则
1.从左到右遍历中缀表达式的每个数字和符号,若是数字就输出(直接成为后缀表达式的一部分,不进入栈)
2.若是符合则判断其与栈顶符号的优先级,是右括号或低于栈顶元素,则栈顶元素依次出栈并输出,等出栈完毕,当前元素入栈。
3.遵循以上两条直到输出后缀表达式为止。
老样子大家直接看动图吧简单粗暴,清晰易懂
#### 后缀表达式计算结果
中缀:9 + ( 3 - 1 ) * 3 + 10 / 2=20
后缀:9 3 1 - 3 * + 10 2 / +
后缀表达式的值也为20,那么我们来了解一下计算机是如何将后缀表达式计算为20的。
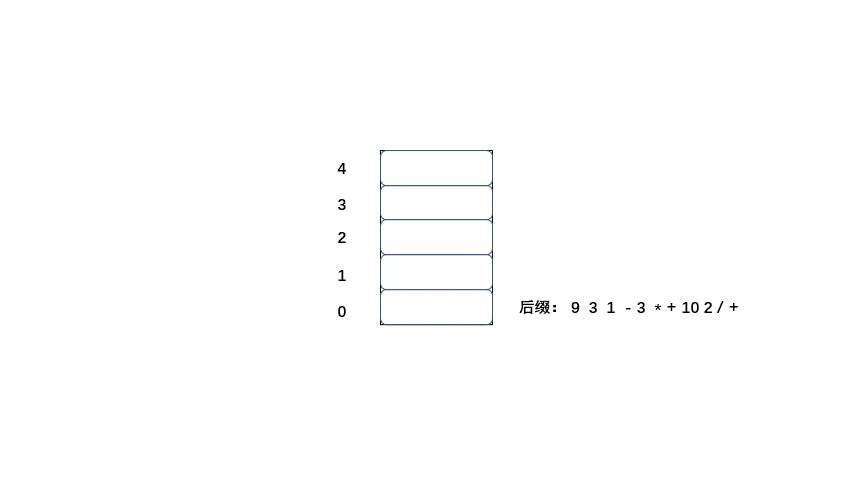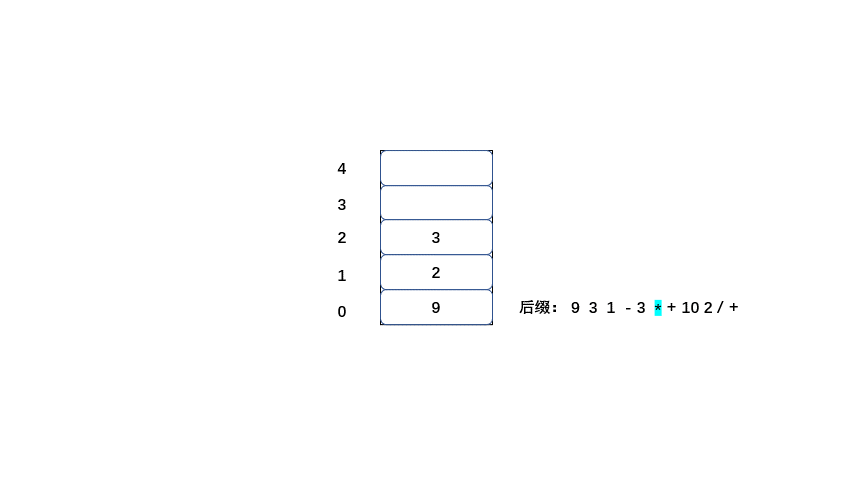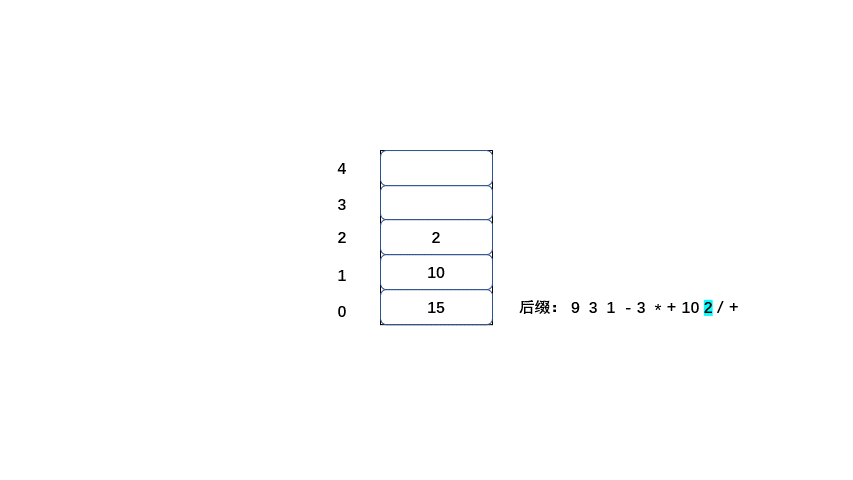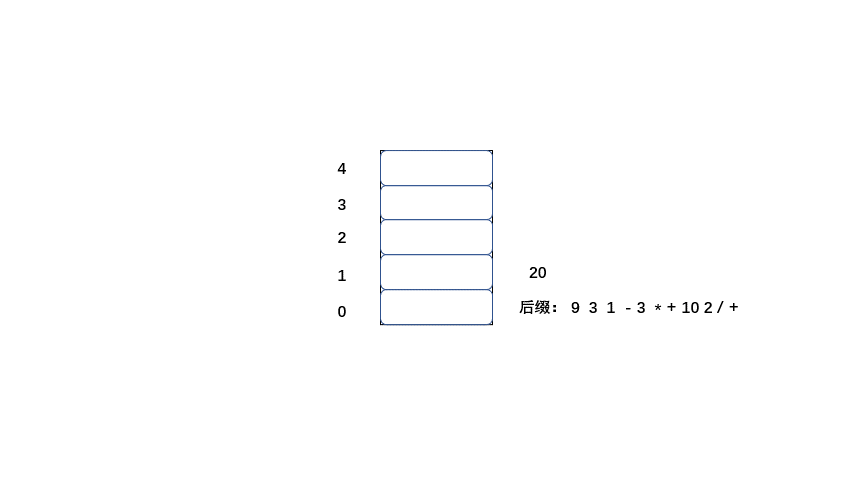
规则:
1.从左到右遍历表达式的每个数字和符号,如果是数字就进栈
2.如果是符号就将栈顶的两个数字出栈,进行运算,并将结果入栈,一直到获得最终结果。
下面大家 继续看动图吧。
注:为了用动图把逻辑整的清晰明了,十几秒的动图,就要整半个多小时,改进好几遍。如果觉得图片对你有帮助的话就点个赞和在看吧。
## 这是队列
### 队列模型
像栈一样,队列(queue)也是表。然而使用队列时插入在一端进行而删除在另一端进行,遵守先进先出的规则。所以队列的另一个名字是(FIFO)。
队列的基本操作是入队(enqueue):它是在表的末端(队尾(rear)插入一个元素。出队(dequeue):出队他是删除在表的开头(队头(front))的元素。
注:下面模型只象征着输入输出操作
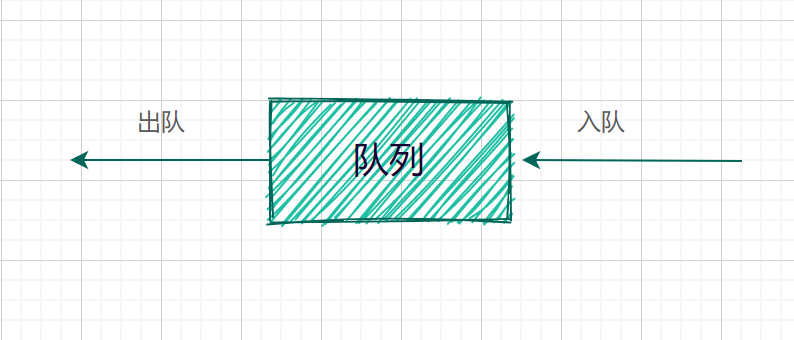
具体模型
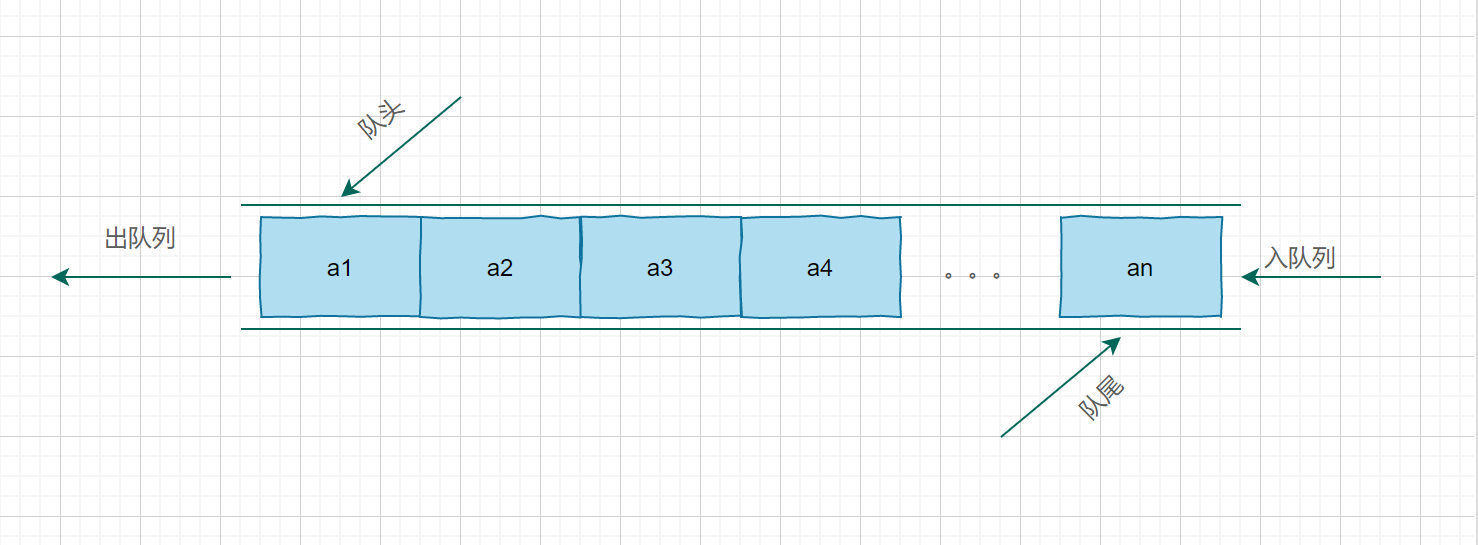
### 队列的实现
队列我们在树的层次遍历时经常使用,后面我们写到树的时候会给大家整理框架。队列同样也可以由数组和LinkedList实现,刷题时比较常用的方法是
```
Queue queue = new LinkedList();
```
### 循环队列
循环队列的出现就是为了解决队列的假溢出问题。何为假溢出呢?我们运用数组实现队列时,数组长度为5,我们放入了[1,2,3,4,5],我们将1,2出队,此时如果继续加入6时,因为数组末尾元素已经被占用,再向后加则会溢出,但是我们的下标0,和下标1还是空闲的。所以我们把这种现象叫做“假溢出”。
例如,我们在学校里面排队洗澡一人一个格,当你来到澡堂发现前面还有两个格,但是后面已经满了,你是去前面洗,还是等后面格子的哥们洗完再洗?肯定是去前面的格子洗。除非澡堂的所有格子都满了。我们才会等。
所以我们用来解决假溢出的方法就是后面满了,就再从头开始,也就是头尾相接的循环,我们把队列的这种头尾相接的顺序存储结构成为循环队列。
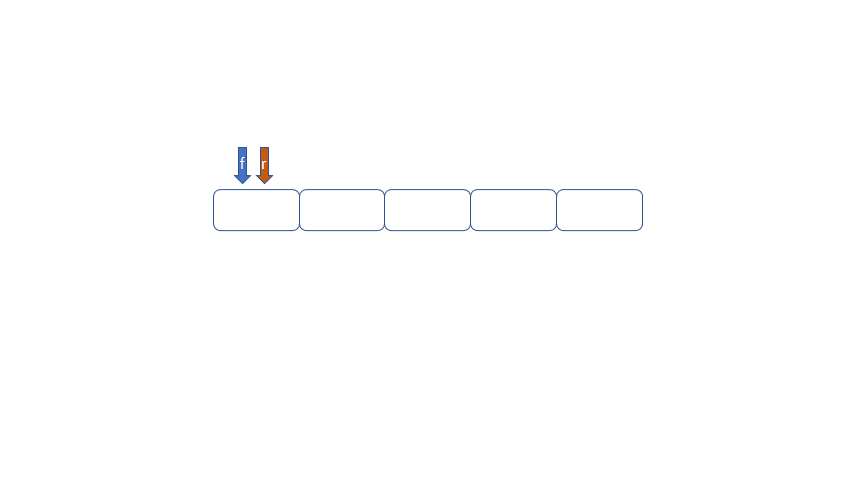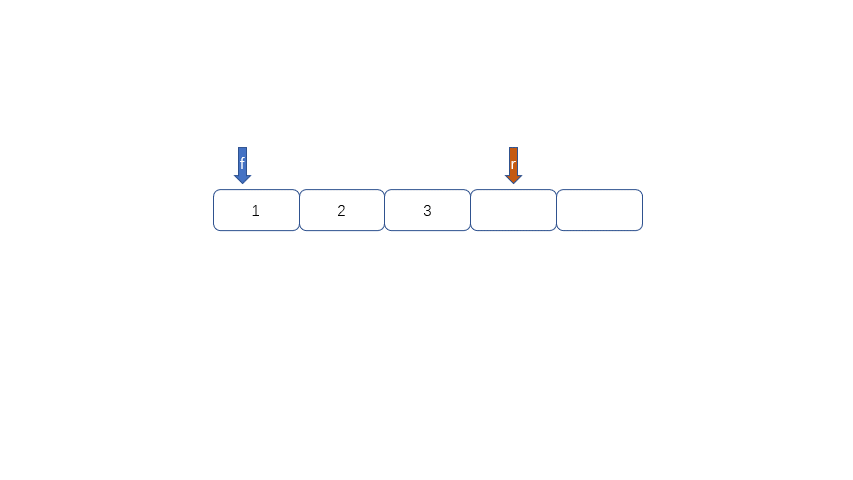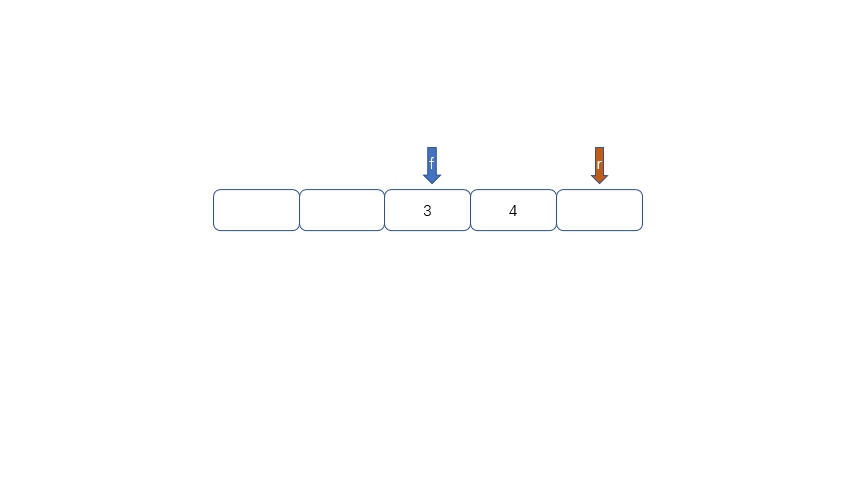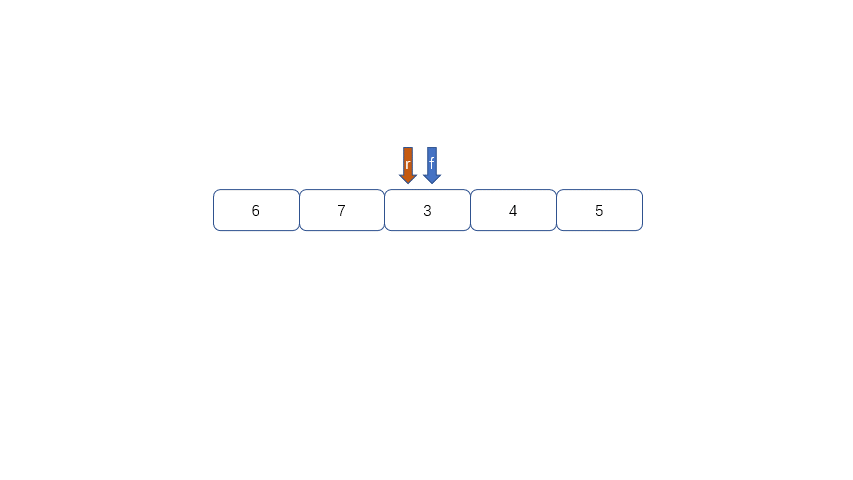
我们发现队列为空时front == rear,队列满时也是front == rear,那么问题来了,我们应该怎么区分满和空呢?
我们可以通过以下两种方法进行区分,
1.设置标记变量flag;当front==rear 时且flag==0时为空,当front==rear且rear为1时且flag==1时为满
2.当队列为空时,front==rear,当队列满是我们保留一个元素空间,也就是说,队列满时,数组内还有一个空间。
例:
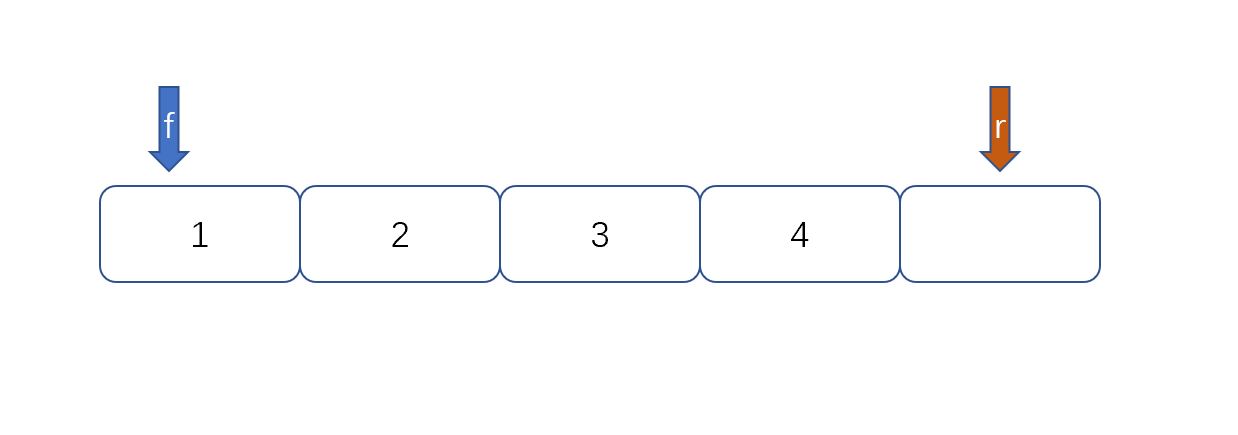
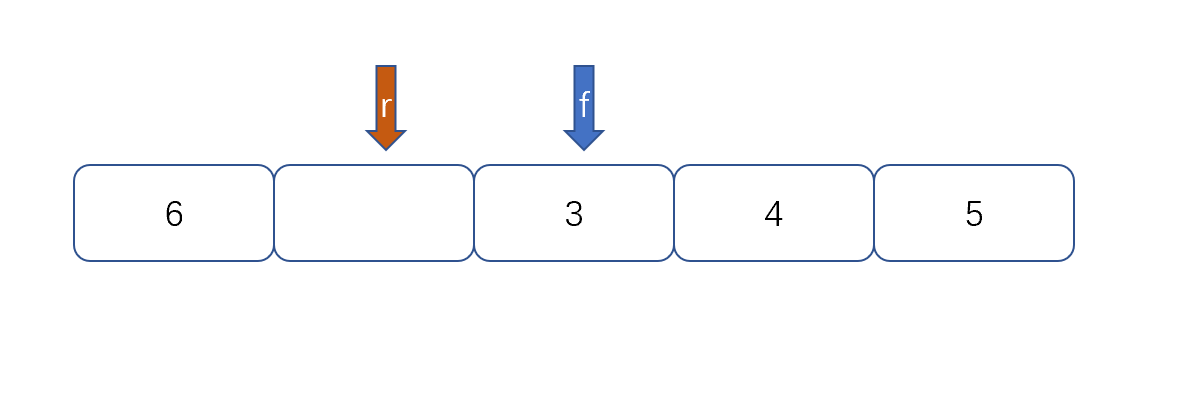
然后我们再根据以下公式则能够判断队列满没满了。
(rear+1)%queuesize==front
queuesize,代表队列的长度,上图为5。我们来判断上面两张图是否满。(4+1)%5==0,(1+1)%5==3
两种情况都是满的,over。
注:为了用动图把逻辑整的清晰明了,十几秒的动图,就要整半个多小时,改进好几遍。如果觉得图片对你有帮助的话就点个赞和在看吧。