> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
>
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
>
> 另外希望手机阅读的同学可以来我的 [**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png) 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)进入。
#### [74. 搜索二维矩阵](https://leetcode-cn.com/problems/search-a-2d-matrix/)\*\*\*\*
下面我们来看一下另外一种变体,如何在二维矩阵里使用二分查找呢?
其实这个很简单,只要学会了二分查找,这个完全可以解决,我们先来看一个例子
我们需要从一个二维矩阵中,搜索是否含有元素 7,我们如何使用二分查找呢?其实我们可以完全将二维矩阵想象成一个有序的一维数组,然后用二分,,比如我们的二维矩阵中,共有 9 个元素,那定义我们的 left = 0,right = 9 - 1= 8,是不是和一维数组定义相同,然后我们求我们的 mid 值, mid = left +((right - left) >> 1)此时 mid = 4 ,但是我们的二维矩阵下标最大是,nums[2,2]呀,你这求了一个 4 ,让我们怎么整呀。如果我们理解了二分查找,那么这个题目考察我们的应该是如何将一维数组的下标,变为 二维坐标。其实也很简单,咱们看哈,此时咱们的 mid = 4,咱们的二维矩阵共有 3 行, 3 列,那我们 mid =4,肯定在第二行,那么这个应该怎么求得呢?
我们可以直接用 (mid/列数),即可,因为我们 mid = 4,4 /3 = 1,说明在 在第二行,那如果 mid = 7 ,7/3=2,在第三行,我们第几行知道了,那么我们如何知道第几列呢?我们可以直接根据 (mid % 列数 )来求得呀,比如我们此时 mid = 7,7%3 = 1,那么在我们一维数组索引为 7 的元素,其处于二维数组的第 2 列,大家看看下图是不是呀!
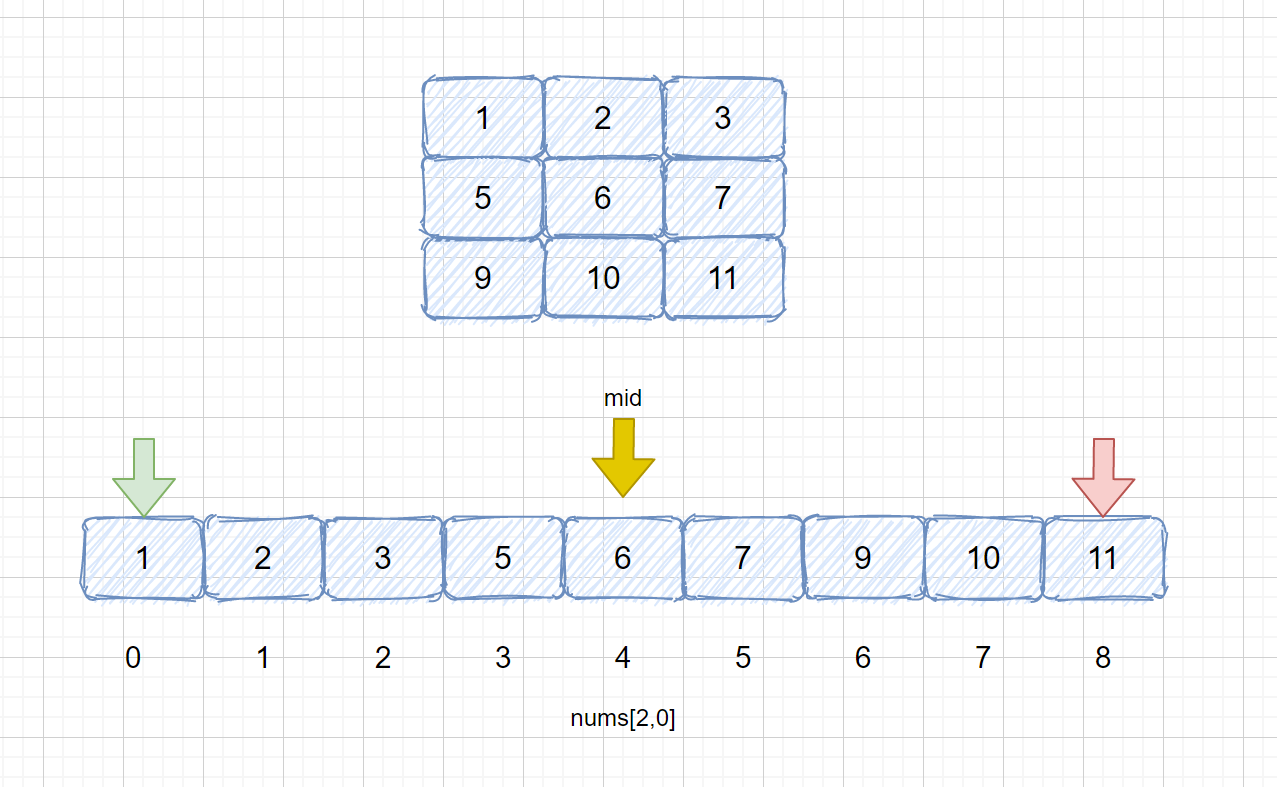
下面我们来看一下 leetcode 74 题,让我们给他整个通透
### 搜索二维矩阵
#### 题目描述
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
示例 1
> 输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
> 输出:true
示例 2
> 输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
> 输出:false
示例 3
> 输入:matrix = [], target = 0
> 输出:false
#### 题目解析
在上面我们已经解释了如何在二维矩阵中进行搜索,这里我们再对其进行一个总结,就是我们凭空想象一个一维数组,这个数组是有二维数组一层一层拼接来的,也是完全有序,然后我们定义两个指针一个指向一维数组头部,一个指向尾部,我们求得 mid 值然后将 mid 变成二维坐标,然后和 target 进行比较,如果大于则移动 left ,如果小于则移动 right 。
动图解析
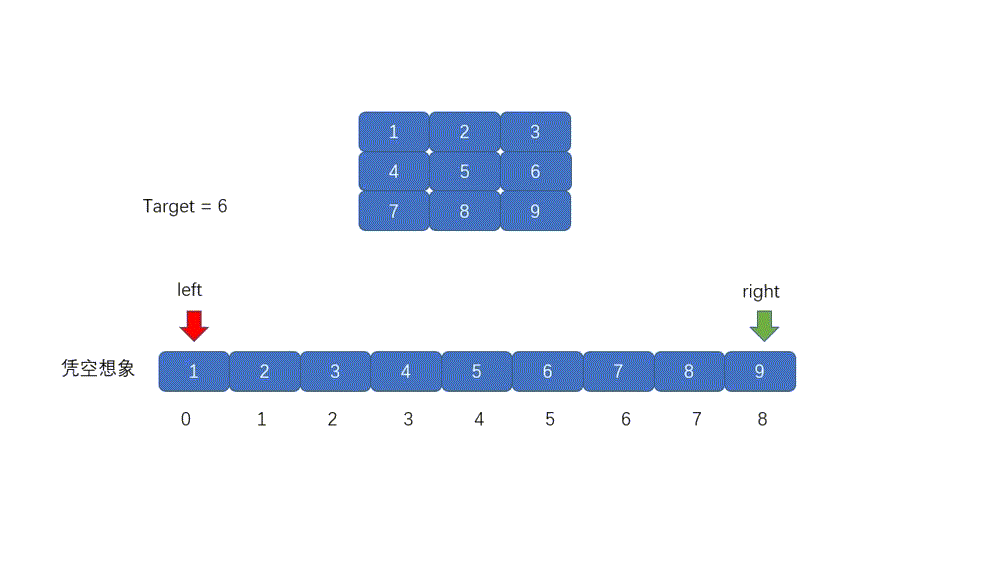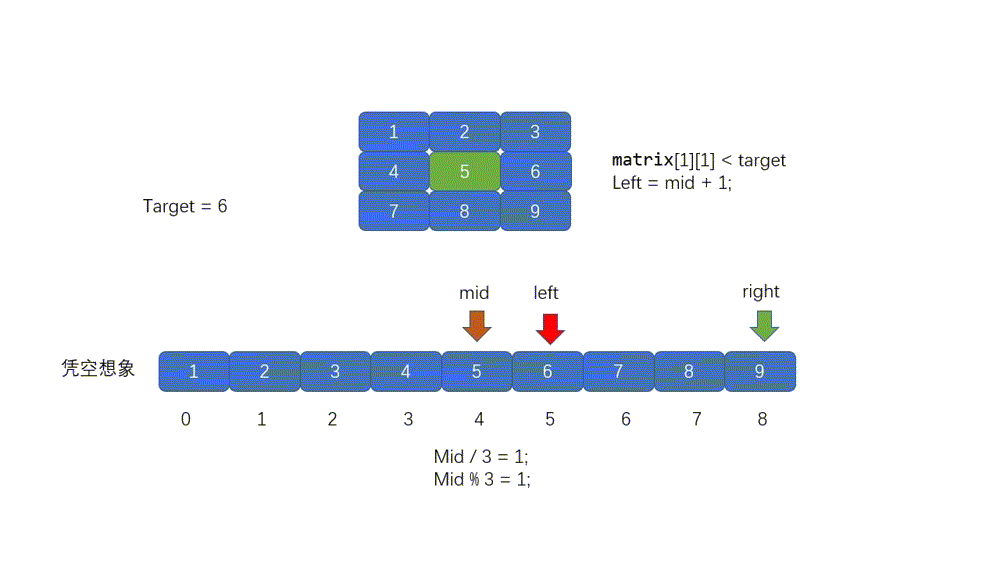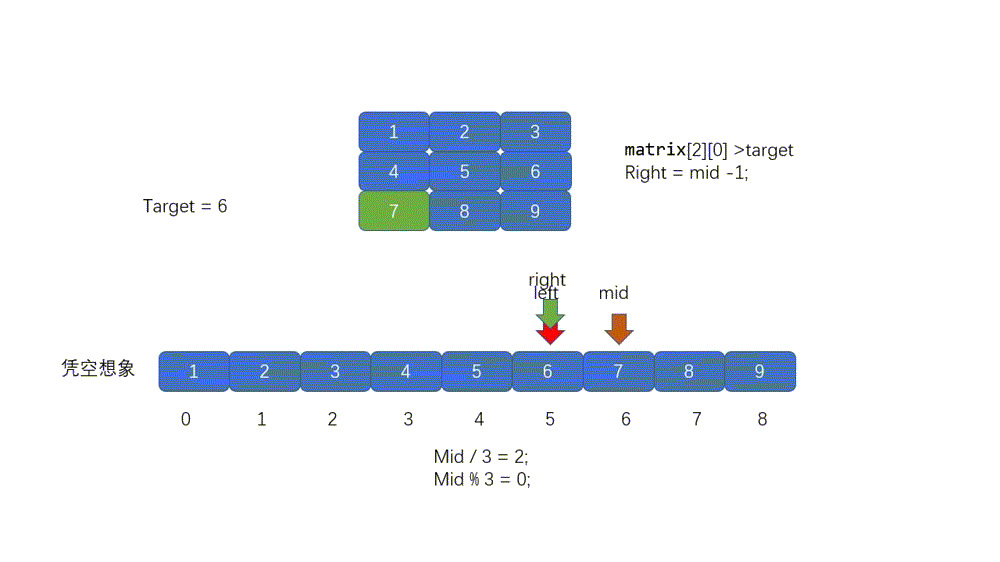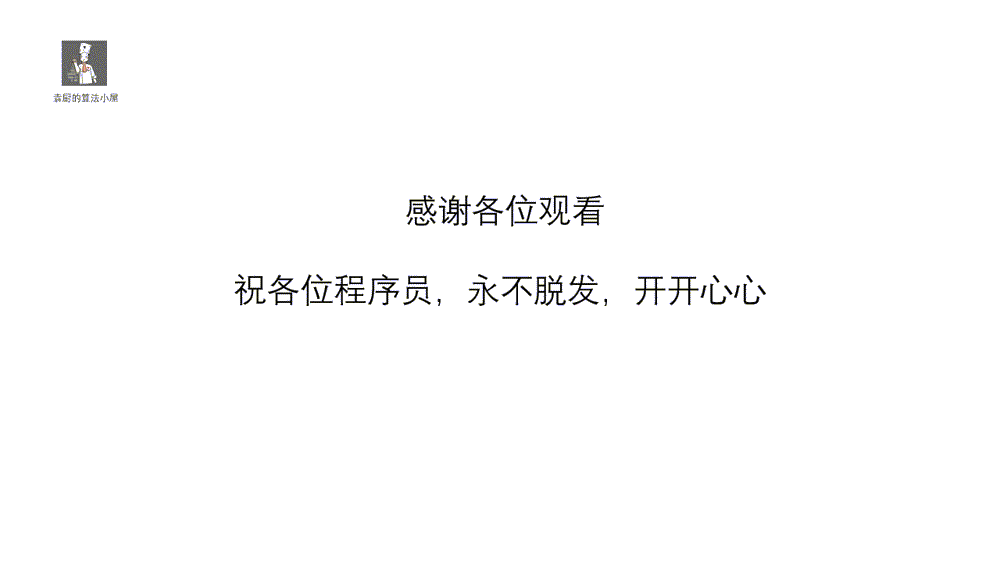
#### 题目代码
Java Code:
```java
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0) {
return false;
}
//行数
int row = matrix.length;
//列数
int col = matrix[0].length;
int left = 0;
//行数乘列数 - 1,右指针
int right = row * col - 1;
while (left <= right) {
int mid = left+ ((right-left) >> 1);
//将一维坐标变为二维坐标
int rownum = mid / col;
int colnum = mid % col;
if (matrix[rownum][colnum] == target) {
return true;
} else if (matrix[rownum][colnum] > target) {
right = mid - 1;
} else if (matrix[rownum][colnum] < target) {
left = mid + 1;
}
}
return false;
}
}
```
Go Code:
```go
func searchMatrix(matrix [][]int, target int) bool {
if len(matrix) == 0 {
return false
}
// 行数
row := len(matrix)
//列数
col := len(matrix[0])
// 行数 * 列数 - 1 为右指针
left, right := 0, row * col - 1
for (left <= right) {
mid := left + ((right - left) >> 1)
//将一维坐标变为二维坐标
rownum := mid / col
colnum := mid % col
if matrix[rownum][colnum] == target {
return true
} else if matrix[rownum][colnum] > target {
right = mid - 1
} else if matrix[rownum][colnum] < target {
left = mid + 1
}
}
return false
}
```