> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
>
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
>
> 另外希望手机阅读的同学可以来我的 [**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png) 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)进入。
# **不完全有序**
## **查找目标元素(不含重复元素)**
之前我们说二分查找需要在完全有序的数组里使用,那么不完全有序时可以用吗?
例:
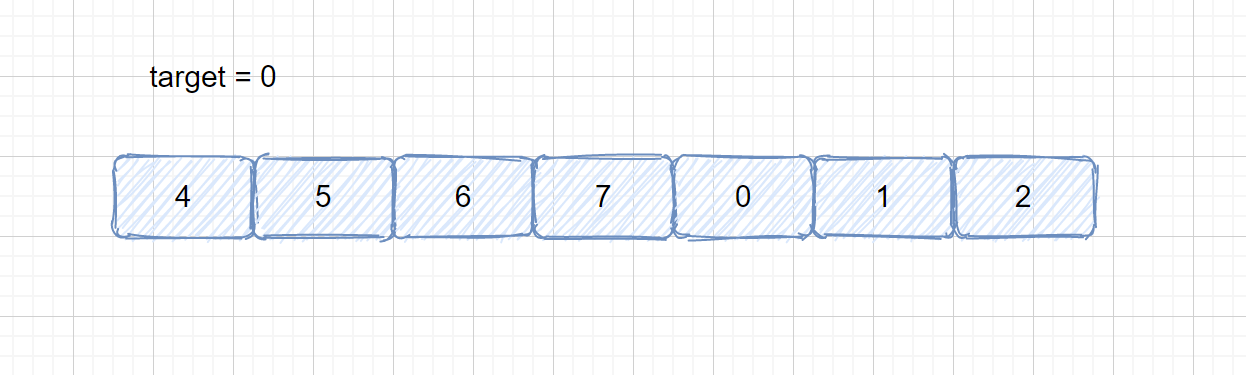
上面的新数组虽然不是完全有序,但是也可以看成是由一个完全有序的数组翻折得到的。或者可以理解成两个有序数组,且第二个数组的最大值小于第一的最小值,我们将其拼接,拼接成了一个不完全有序的数组,在这个数组中我们需要找到 target ,找到后返回其索引,如果没有找到则返回 -1;
我们第一次看到这种题目时,可能会想到,我们只需要挨个遍历就好啦,发现后返回索引即可,这样做当然是可以滴,那么我们可不可以使用二分查找呢?
下面我们看一下解决该题的具体思路。
首先我们设想一下 mid 值会落到哪里,我们一起来想一下。
是不是只有两种情况,和 left 在一个数组,同时落在 数组 1 或同时在 数组 2,或者不在一个数组, left 在数组 1,mid 在数组 2。想到这里咱们这个题目已经完成一半了。
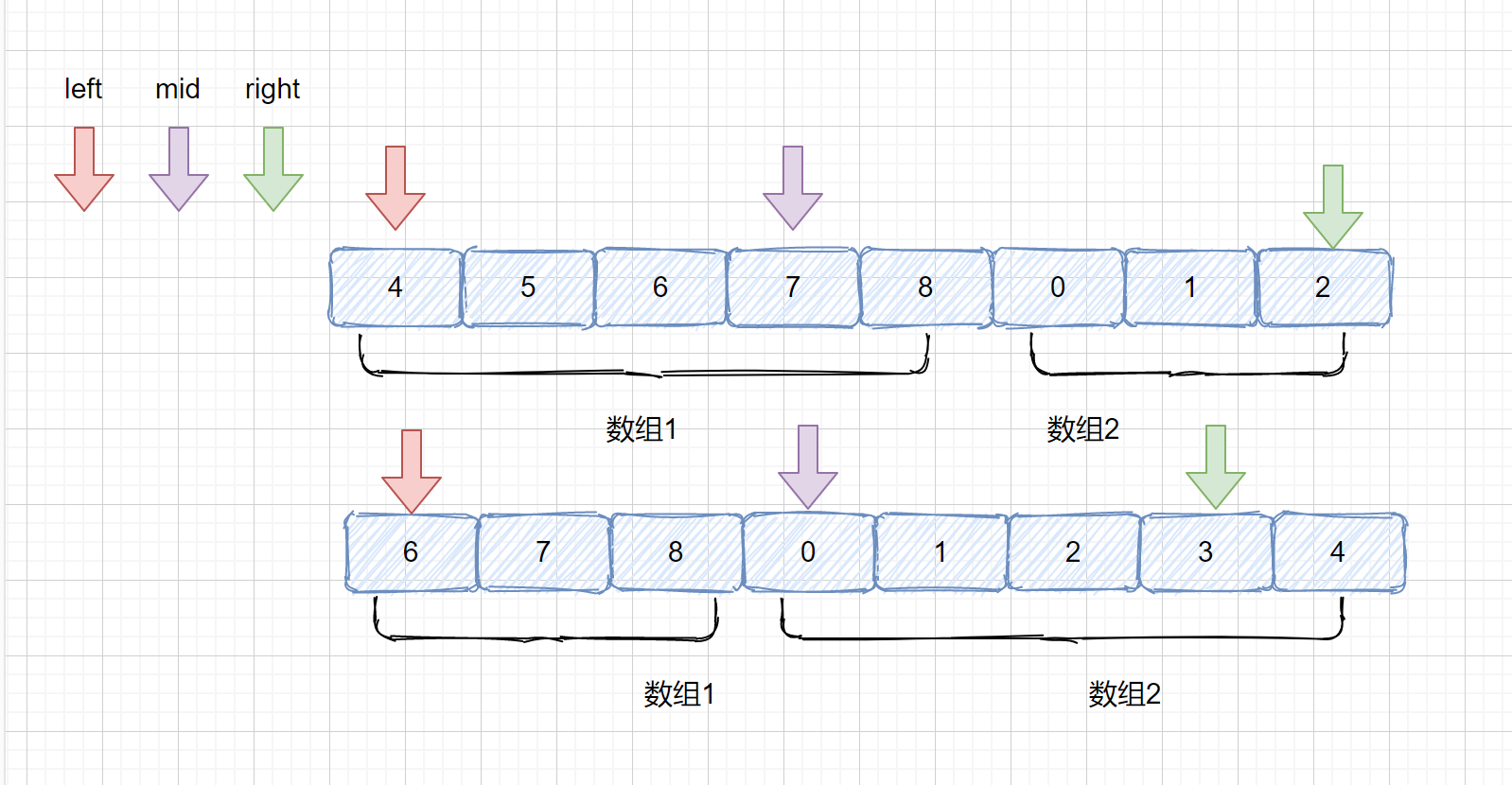
那么我们先来思考一下,?我们可以根据 nums[mid] 和 nums[left] 判断,是因为我们的 mid 一定是会落在 left 和 right 之间,那如果 nums[mid] >= nums[left] 时,说明他俩落在一个数组里了,如果 nums[mid] < nums[left] 时,说明他俩落在了不同的数组,此时 left 在数组 1 mid 在数组 2.
注:left 和 mid 落在同一数组时,不能是 left 在 数组 2 ,mid 在 数组 1 呢?因为咱们的 mid 是通过 left 和 right 的下标求得,所以应该在 left 和 right 中间
如果我们的 mid 和 left 在同一个数组内时?咱们的 target 会有几种情况呢?我们通过都落在 数组 1 举例。
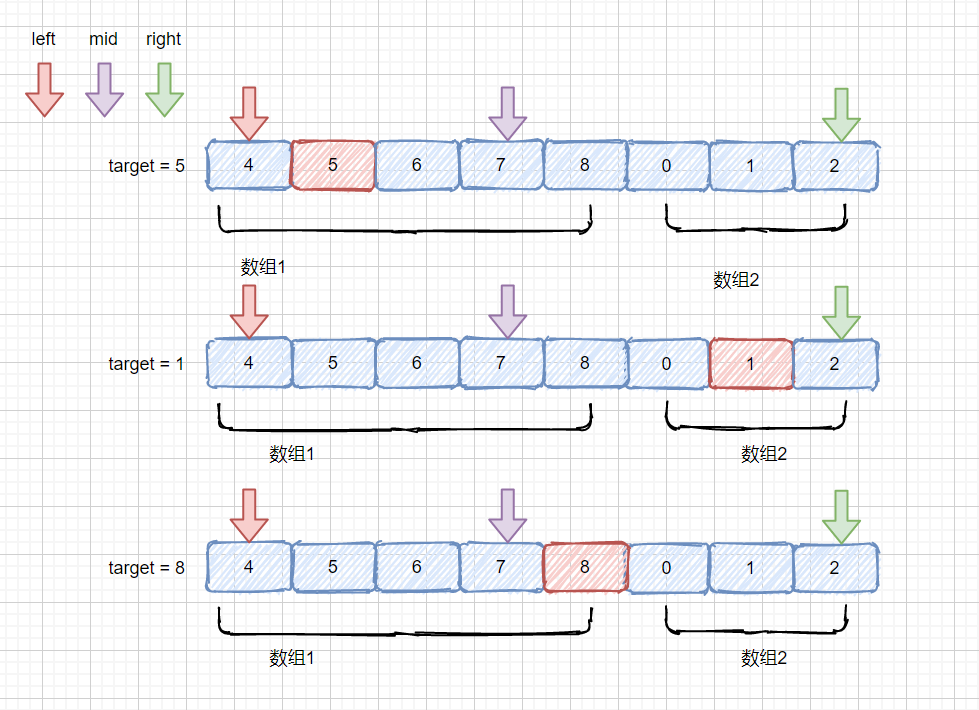
无非也是两种情况,用我们上面的例子来说,
1.**落在 mid 的左边**,当前例子中 情况是落在 [4,7)区间内,即 4 <= target < 7 ,也就是 target >= nums[left] && target < nums[mid],此时我们让 right = mid -1,让 left 和 right 都落到数组 1 中,下次查找我们就是在数组 1 中进行了,完全有序,
2.**落在 mid 的右边**,此时例子中 target 不落在 [4,7)区间内,那就 target = 8 或 0 <= target <= 2 (此时我们的 target 均小于 nums[left]) 两种情况,也就是 target > nums[mid] || target < nums[left] 此时我们让 left = mid + 1 即可,也是为了慢慢将 left 和 right 指针赶到一个有序数组内。
那我们在来思考一下当 mid 值落在 **数组 2** 中时,target 会有几种情况呢?其实和上面的例子思路一致,情况相反而已。
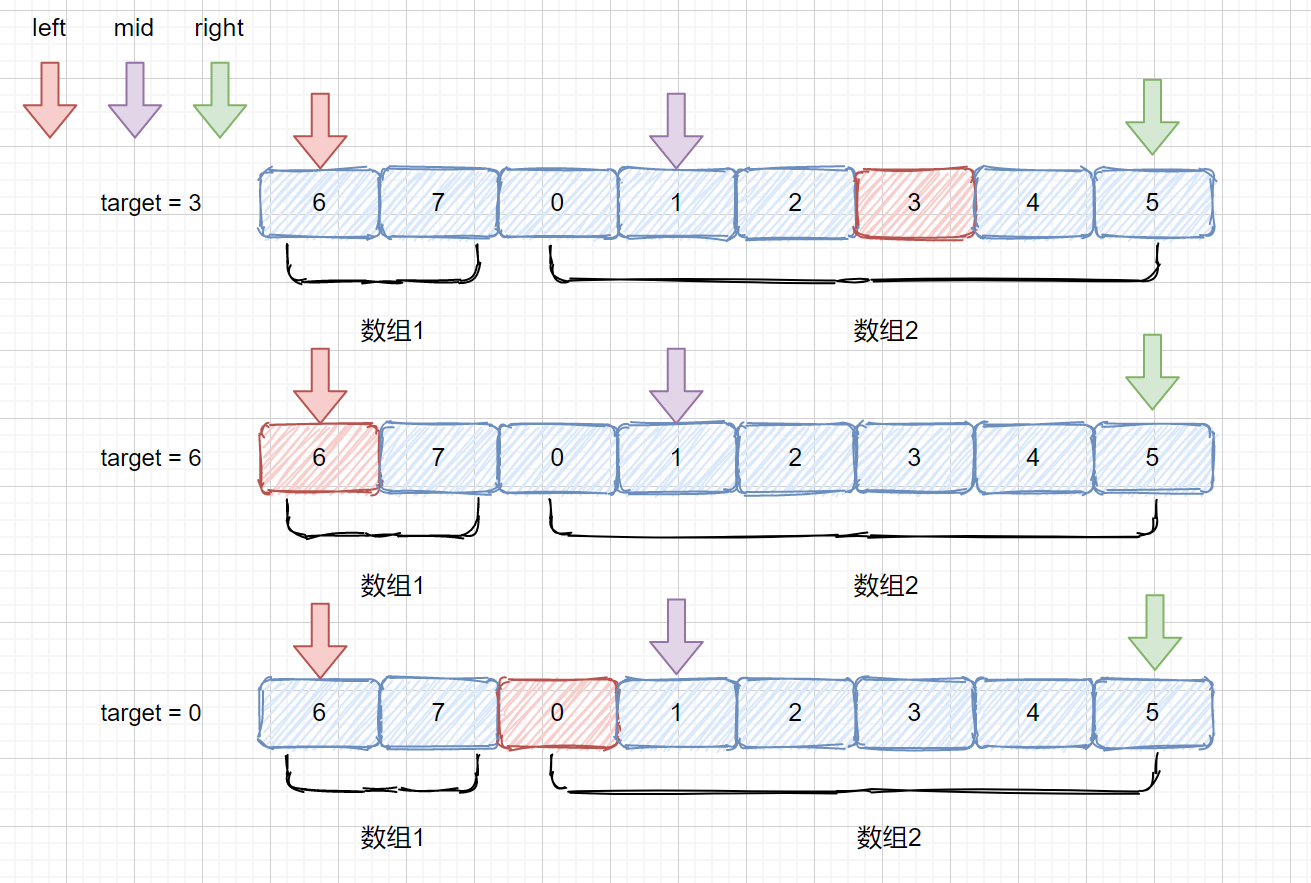
1. target <= nums[right] && target > nums[mid]
> 这里和上面的对应,此时的情况就是整个落在右半部分,我们下次就可以在数组 2 内进行查找。
2. target > nums[right] || target < nums[mid]
> 这里就是和上面的第二种情况对应,落在 mid 的左半部分,我们尽量将两个指针赶到一起
希望我的表达能够让大家对这个变种理解透彻,如果没能让各位理解,或者有表达不当的地方欢迎各位批评指导。然后我们一起来做一下 leetcode 33 题吧。
#### [33. 搜索旋转排序数组](https://leetcode-cn.com/problems/search-in-rotated-sorted-array/)
#### 题目描述
给你一个整数数组 nums ,和一个整数 target 。
该整数数组原本是按升序排列,但输入时在预先未知的某个点上进行了旋转。(例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请你在数组中搜索 target ,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
示例 1:
> 输入:nums = [4,5,6,7,0,1,2], target = 0
> 输出:4
示例 2:
> 输入:nums = [4,5,6,7,0,1,2], target = 3
> 输出:-1
示例 3:
> 输入:nums = [1], target = 0
> 输出:-1
#### 题目解析
这个题目的解答方法,咱们在上面已经有所描述,下面我们来看一下下面这个例子的代码执行过程吧.
> 输入 nums = [4,5,6,7,8,0,1,2] target = 8
下面我们看题目代码吧,如果还没有完全理解的同学,可以仔细阅读 if ,else if 里面的语句,还有注释,一定可以整透的。
#### 题目代码
Java Code:
```java
class Solution {
public int search(int[] nums, int target) {
//左右指针
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left+((right-left)>>1);
if (nums[mid] == target) {
return mid;
}
//落在同一数组的情况,同时落在数组1 或 数组2
if (nums[mid] >= nums[left]) {
//target 落在 left 和 mid 之间,则移动我们的right,完全有序的一个区间内查找
if (nums[mid] > target && target >= nums[left]) {
right = mid - 1;
// target 落在right和 mid 之间,有可能在数组1, 也有可能在数组2
} else if (target > nums[mid] || target < nums[left]) {
left = mid + 1;
}
//不落在同一数组的情况,left 在数组1, mid 落在 数组2
}else if (nums[mid] < nums[left]) {
//有序的一段区间,target 在 mid 和 right 之间
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
// 两种情况,target 在left 和 mid 之间
} else if (target < nums[mid] || target > nums[right]) {
right = mid - 1;
}
}
}
//没有查找到
return -1;
}
}
```
Go Code:
```go
func search(nums []int, target int) int {
// 左右指针
left := 0
right := len(nums) - 1
for (left <= right) {
mid := left + ((right - left) >> 1)
rightNum, leftNum, midNum := nums[right], nums[left], nums[mid]
if midNum == target {
return mid
}
//落在同一数组的情况,同时落在数组1 或 数组2
if midNum >= leftNum {
//target 落在 left 和 mid 之间,则移动我们的right,完全有序的一个区间内查找
if midNum > target && target >= leftNum {
right = mid - 1
} else {
// target落在另一个无序区间, 但和原数组的性质相符, 所以可以继续循环
left = mid + 1
}
} else {
//target 落在 mid 和 right 之间,则移动我们的left,完全有序的一个区间内查找
if midNum < target && target <= rightNum {
left = mid + 1
} else {
// target落在另一个无序区间, 但和原数组的性质相符, 所以可以继续循环
right = mid - 1
}
}
}
return -1
}
```