algorithm-base/animation-simulation/数组篇/leetcode1052爱生气的书店老板.md

如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友 tan45du_one ，备注 github + 题目 + 问题 向我反馈

感谢支持，该仓库会一直维护，希望对各位有一丢丢帮助。

另外希望手机阅读的同学可以来我的 公众号：程序厨 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击刷题小队进入。

1052. 爱生气的书店老板

题目描述

今天，书店老板有一家店打算试营业 customers.length 分钟。每分钟都有一些顾客（customers[i]）会进入书店，所有这些顾客都会在那一分钟结束后离开。

在某些时候，书店老板会生气。 如果书店老板在第 i 分钟生气，那么 grumpy[i] = 1，否则 grumpy[i] = 0。 当书店老板生气时，那一分钟的顾客就会不满意，不生气则他们是满意的。

书店老板知道一个秘密技巧，能抑制自己的情绪，可以让自己连续 X 分钟不生气，但却只能使用一次。

请你返回这一天营业下来，最多有多少客户能够感到满意的数量。

示例：

输入：customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], X = 3 输出：16

解释： 书店老板在最后 3 分钟保持冷静。 感到满意的最大客户数量 = 1 + 1 + 1 + 1 + 7 + 5 = 16.

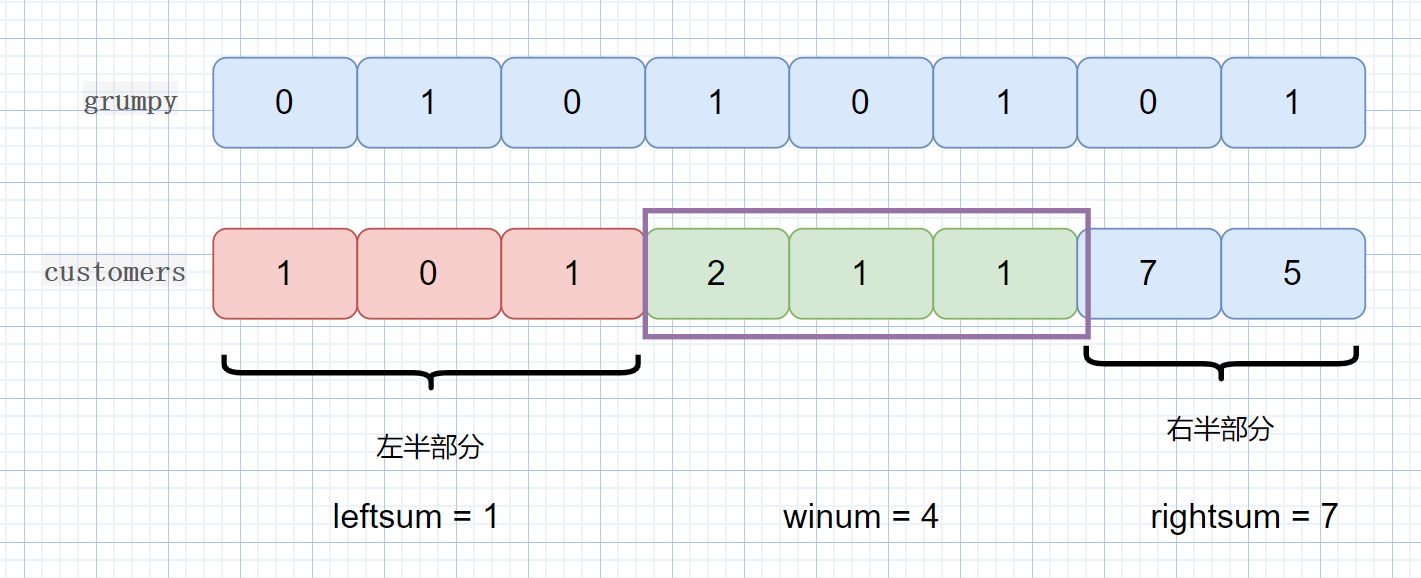
该题目思想就是，我们将 customer 数组的值分为三部分， leftsum, winsum, rightsum。我们题目的返回值则是三部分的最大和。

注意这里的最大和，我们是怎么计算的。

winsum 是窗口内的所有值，不管 grumpy[i] 的值是 0 还是 1,窗口的大小，就对应 K 的值，也就是老板的技能发动时间，该时间段内，老板不会生气，所以为所有的值。

leftsum 是窗口左边区间的值，此时我们不能为所有值，只能是 grumpy[i] == 0 时才可以加入，因为此时不是技能发动期，老板只有在 grumpy[i] == 0 时，才不会生气。

rightsum 是窗口右区间的值，和左区间加和方式一样。那么我们易懂一下窗口，我们的 win 值和 leftsum 值，rightsum 值是怎么变化的呢？

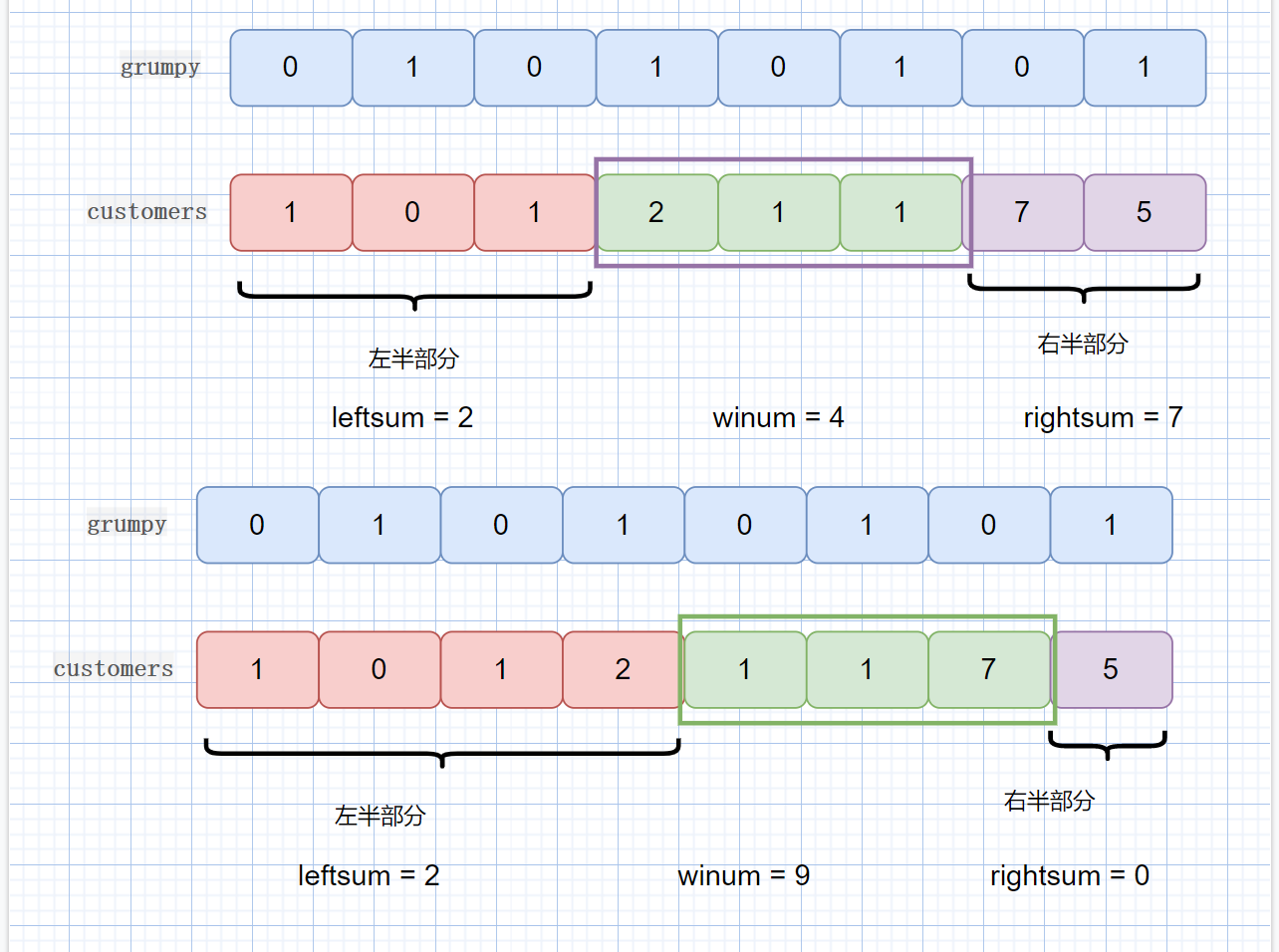
见下图

我们此时移动了窗口，

则左半区间范围扩大，但是 leftsum 的值没有变，这时因为新加入的值，所对应的 grumpy[i] == 1，所以其值不会发生改变，因为我们只统计 grumpy[i] == 0 的值，

右半区间范围减少，rightsum 值也减少，因为右半区间减小的值，其对应的 grumpy[i] == 0，所以 rightsum -= grumpy[i]。

winsum 也会发生变化， winsum 需要加上新加入窗口的值，减去刚离开窗口的值, 也就是 customer[left-1]，left 代表窗口左边缘。

好啦，知道怎么做了，我们直接开整吧。

Java Code:

class Solution {
    public int maxSatisfied(int[] customers, int[] grumpy, int X) {

        int winsum = 0;
        int rightsum = 0;
        int len = customers.length;
        //右区间的值
        for (int i = X; i < len; ++i) {
            if (grumpy[i] == 0) {
                rightsum += customers[i];
            }
        }
        //窗口的值
        for (int i = 0; i < X; ++i) {
              winsum += customers[i];
        }
        int leftsum = 0;
        //窗口左边缘
        int left = 1;
        //窗口右边缘
        int right = X;
        int maxcustomer = winsum + leftsum + rightsum;
        while (right < customers.length) {
            //重新计算左区间的值，也可以用 customer 值和 grumpy 值相乘获得
            if (grumpy[left-1] == 0) {
                leftsum += customers[left-1];
            }
            //重新计算右区间值
            if (grumpy[right] == 0) {
                rightsum -= customers[right];
            }
            //窗口值
            winsum = winsum - customers[left-1] + customers[right];
            //保留最大值
            maxcustomer = Math.max(maxcustomer,winsum+leftsum+rightsum);
            //移动窗口
            left++;
            right++;
        }
        return maxcustomer;
    }
}

Python3 Code:

class Solution:
    def maxSatisfied(self, customers: List[int], grumpy: List[int], X: int) -> int:
        t = ans = sum(customers[:X]) + sum(map(lambda x: customers[X+x[0]] if x[1] == 0 else 0, enumerate(grumpy[X:])))
        for j in range(X, len(customers)):
            t += customers[j] * grumpy[j] - customers[j-X] * grumpy[j-X]
            ans = max(ans, t)
        return ans

Swift Code

class Solution {
    func maxSatisfied(_ customers: [Int], _ grumpy: [Int], _ minutes: Int) -> Int {
        let len = customers.count
        var winSum = 0, rightSum = 0, leftSum = 0
        // 右区间的值
        for i in minutes..<len {
            if grumpy[i] == 0 {
                rightSum += customers[i]
            }
        }
        // 窗口的值
        for i in 0..<minutes {
            winSum += customers[i]
        }
        var maxCustomer = winSum + leftSum + rightSum
        // 窗口左边缘
        var left = 1, right = minutes
        while right < len {
            // 重新计算左区间的值，也可以用 customer 值和 grumpy 值相乘获得
            if grumpy[left - 1] == 0 {
                leftSum += customers[left - 1]
            }
            // 重新计算右区间值
            if grumpy[right] == 0 {
                rightSum -= customers[right]
            }
            // 窗口值
            winSum = winSum - customers[left - 1] + customers[right]
            maxCustomer = max(maxCustomer, winSum + leftSum + rightSum) // 保留最大值
            // 移动窗口
            left += 1
            right += 1
        }

        return maxCustomer
    }
}

C++ Code

class Solution
{
public:
    int maxSatisfied(vector<int> &customers, vector<int> &grumpy, int minutes)
    {
        for_each(grumpy.begin(), grumpy.end(), [](auto &g){ g = !g; });
        vector<int> osum(customers.size(), 0);

        //先初始化第一个元素
        osum[0] = customers[0] * grumpy[0];
        //计算前缀和, osum是origin sum
        for (int i = 1; i < osum.size(); i++)
        {
            osum[i] = osum[i - 1] + customers[i] * grumpy[i];
        }

        //计算连续minutes的和
        vector<int> msum(customers.size() - minutes + 1, 0);
        for (int i = 0; i < minutes; i++)
        {
            msum[0] += customers[i];
        }
        for (int i = 1; i < msum.size(); i++)
        {
            msum[i] = msum[i - 1] - customers[i - 1] + customers[i + minutes - 1];
        }

        //分成三段计算
        int result = 0;
        for (int i = 0; i < msum.size(); i++)
        {
            //左                                         中         右
            //注意左的边界条件, 可以使用边界测试
            int sum = ((i - 1 >= 0) ? osum[i - 1] : 0) + msum[i] + osum[osum.size() - 1] - osum[i + minutes - 1];
            if (sum > result)
                result = sum;
        }

        return result;
    }
};