algorithm-base/animation-simulation/数据结构和算法/BM.md

## BM 算法(Boyer-Moore)

> 如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ，备注 github + 题目 + 问题 向我反馈
>
> 感谢支持，该仓库会一直维护，希望对各位有一丢丢帮助。
>
> 另外希望手机阅读的同学可以来我的 <u>[**公众号：袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。

我们刚才说过了 BF 算法，但是 BF 算法是有缺陷的，比如我们下面这种情况

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210401200433751.png)

如上图所示，如果我们利用 BF 算法，遇到不匹配字符时，每次右移一位模式串，再重新从头进行匹配，我们观察一下，我们的模式串 abcdex 中每个字符都不一样，但是我们第一次进行字符串匹配时，abcde 都匹配成功，到 x 时失败，又因为模式串每位都不相同，所以我们不需要再每次右移一位，再重新比较，我们可以直接跳过某些步骤。如下图

![BM2](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/BM2.141fhslg6vek.png)

我们可以跳过其中某些步骤，直接到下面这个步骤。那我们是依据什么原则呢？

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210401200635476.png)

### 坏字符规则

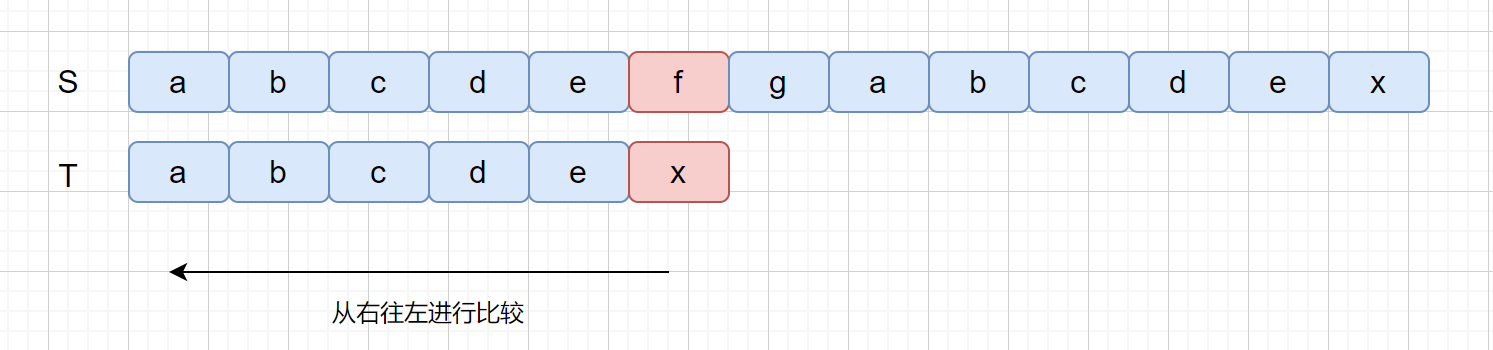
我们之前的 BF 算法是从前往后进行比较 ，BM 算法是从后往前进行比较，我们来看一下具体过程，我们还是利用上面的例子。

![BM4](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/BM4.2mayfaccj3i0.png)

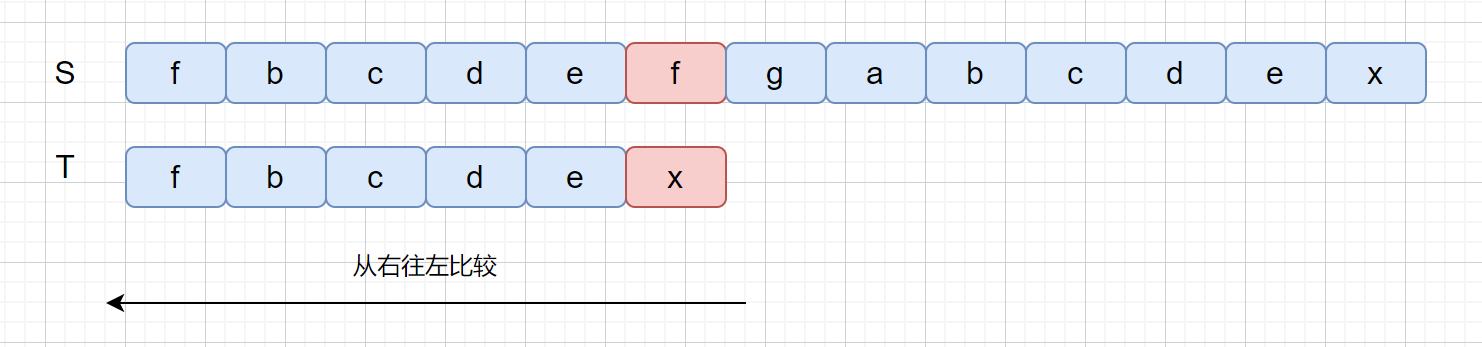
BM 算法是从后往前进行比较，此时我们发现比较的第一个字符就不匹配，我们将**主串**这个字符称之为**坏字符**，也就是 f ,我们发现坏字符之后，模式串 T 中查找是否含有该字符（f），我们发现并不存在 f，此时我们只需将模式串右移到坏字符的后面一位即可。如下图

![BM5](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/BM5.31j3sja7vsq0.png)

那我们在模式串中找到坏字符该怎么办呢？

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210401200838199.png)

此时我们的坏字符为 f ,我们在模式串中，查找发现含有坏字符 f,我们则需要移动模式串 T ,将模式串中的 f 和坏字符对齐。见下图。

![坏字符移动](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/坏字符移动.kl5k3nnzkcg.png)

然后我们继续从右往左进行比较，发现 d 为坏字符，则需要将模式串中的 d 和坏字符对齐。

![换字符对其2](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/换字符对其2.4xdb38am9e60.png)

![坏字符原则](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/坏字符原则.781vhv3vm280.png)

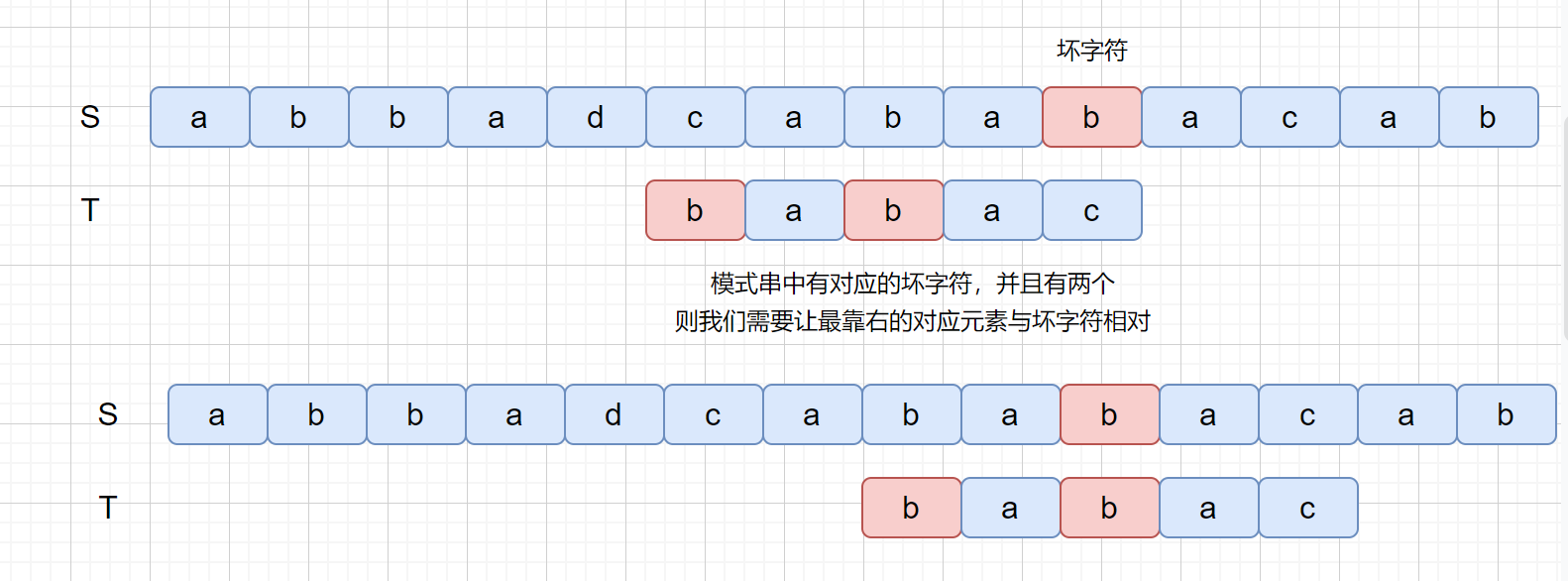
那么我们在来思考一下这种情况，那就是模式串中含有多个坏字符怎么办呢？

![两个坏字符](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/两个坏字符.1a6hcs8ildkw.png)

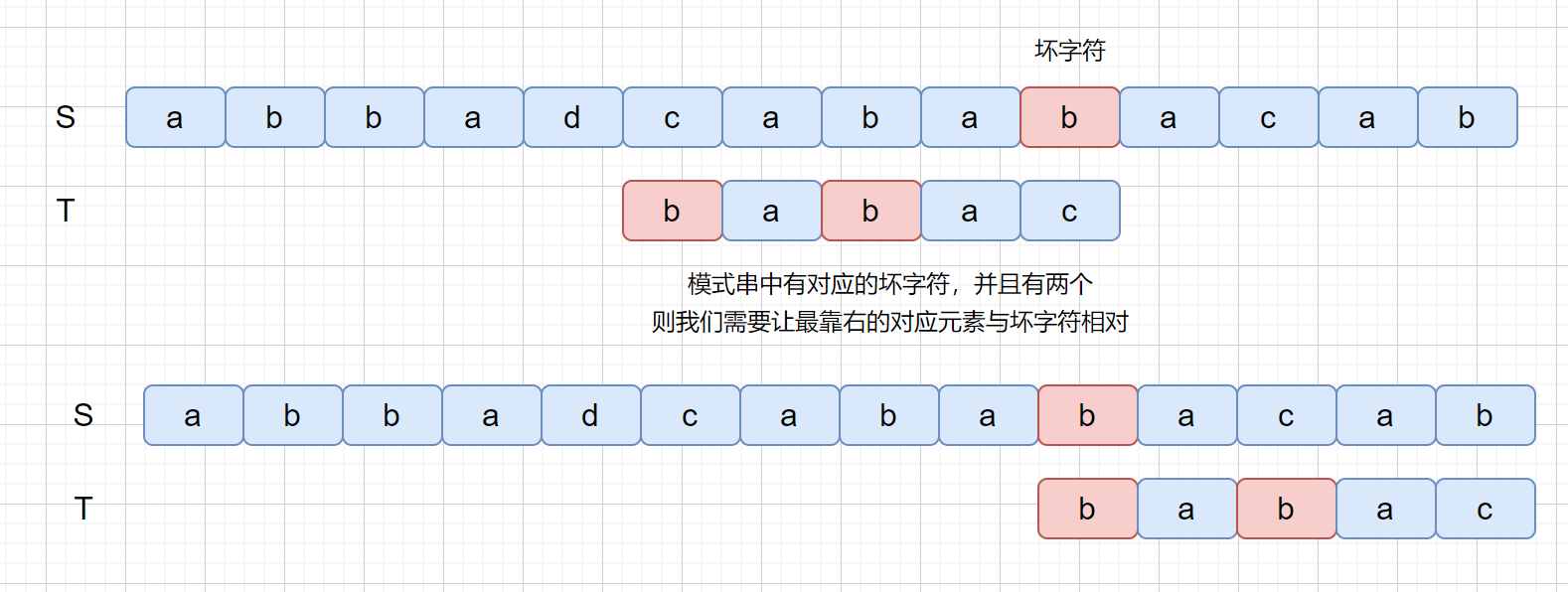
那么我们为什么要让**最靠右的对应元素与坏字符匹配**呢？如果上面的例子我们没有按照这条规则看下会产生什么问题。

![坏字符匹配不按规则](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/坏字符匹配不按规则.1y45278xg1vk.png)

如果没有按照我们上述规则，则会**漏掉我们的真正匹配**。我们的主串中是**含有 babac** 的，但是却**没有匹配成功**，所以应该遵守**最靠右的对应字符与坏字符相对**的规则。

我们上面一共介绍了三种移动情况，分别是下方的模式串中没有发现与坏字符对应的字符，发现一个对应字符，发现两个。这三种情况我们分别移动不同的位数，那我们是根据依据什么来决定移动位数的呢？下面我们给图中的字符加上下标。见下图

![坏字符移动规则](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/坏字符移动规则.48oh1msdypy0.png)

下面我们来考虑一下这种情况。

![换字符bug](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/换字符bug.24av6jslzh40.png)

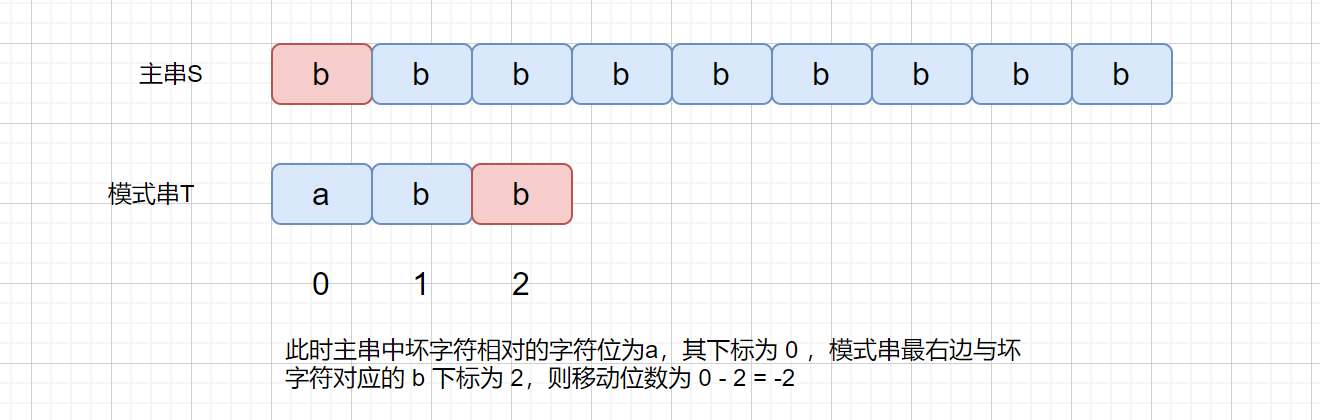
此时这种情况肯定是不行的，不往右移动，甚至还有可能左移，那么我们有没有什么办法解决这个问题呢？继续往下看吧。

### 好后缀规则

好后缀其实也很容易理解，我们之前说过 BM 算法是从右往左进行比较，下面我们来看下面这个例子。

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210401201215799.png)

这里如果我们按照坏字符进行移动是不合理的，这时我们可以使用好后缀规则，那么什么是好后缀呢？

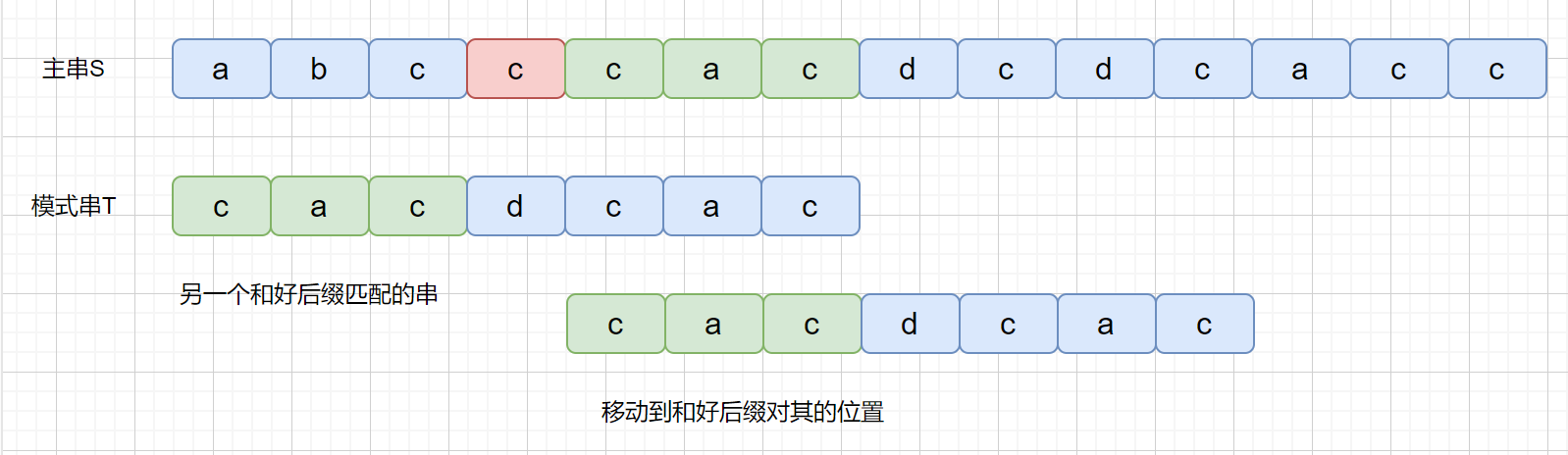
BM 算法是从右往左进行比较，发现坏字符的时候此时 cac 已经匹配成功，在红色阴影处发现坏字符。此时已经匹配成功的 cac 则为我们的好后缀，此时我们拿它在模式串中查找，如果找到了另一个和好后缀相匹配的串，那我们就将另一个和**好后缀相匹配**的串 ，滑到和好后缀对齐的位置。

是不是感觉有点拗口，没关系，我们看下图，红色代表坏字符，绿色代表好后缀

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210401201254453.png)

![](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/好后缀中间.7b6m6ki25l00.png)

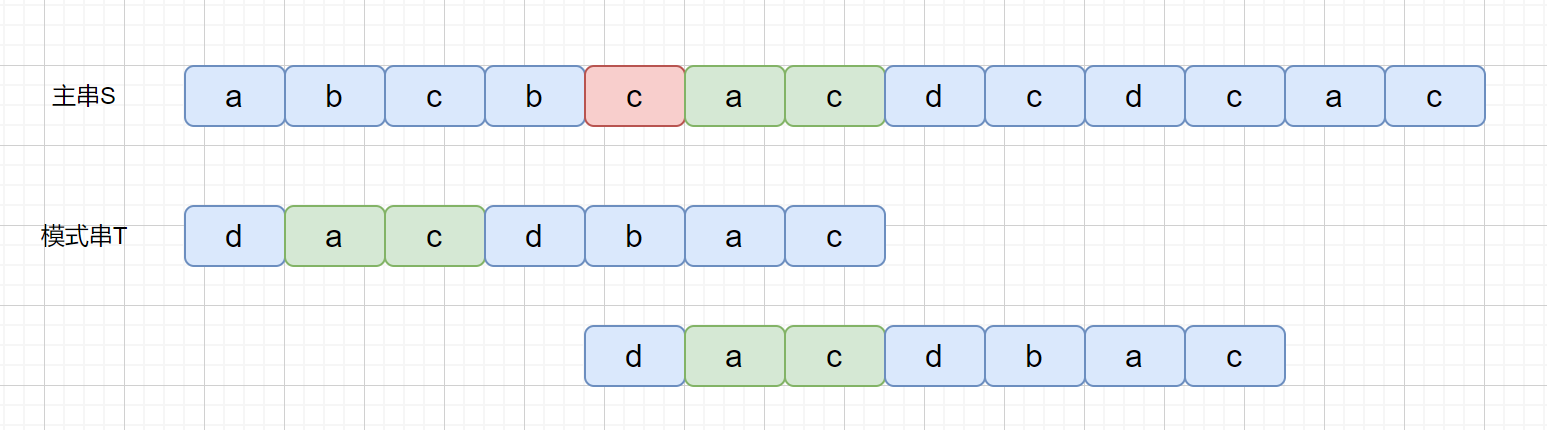
上面那种情况搞懂了，但是我们思考一下下面这种情况

![比较](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/比较.4m9ci1x1c1e0.png)

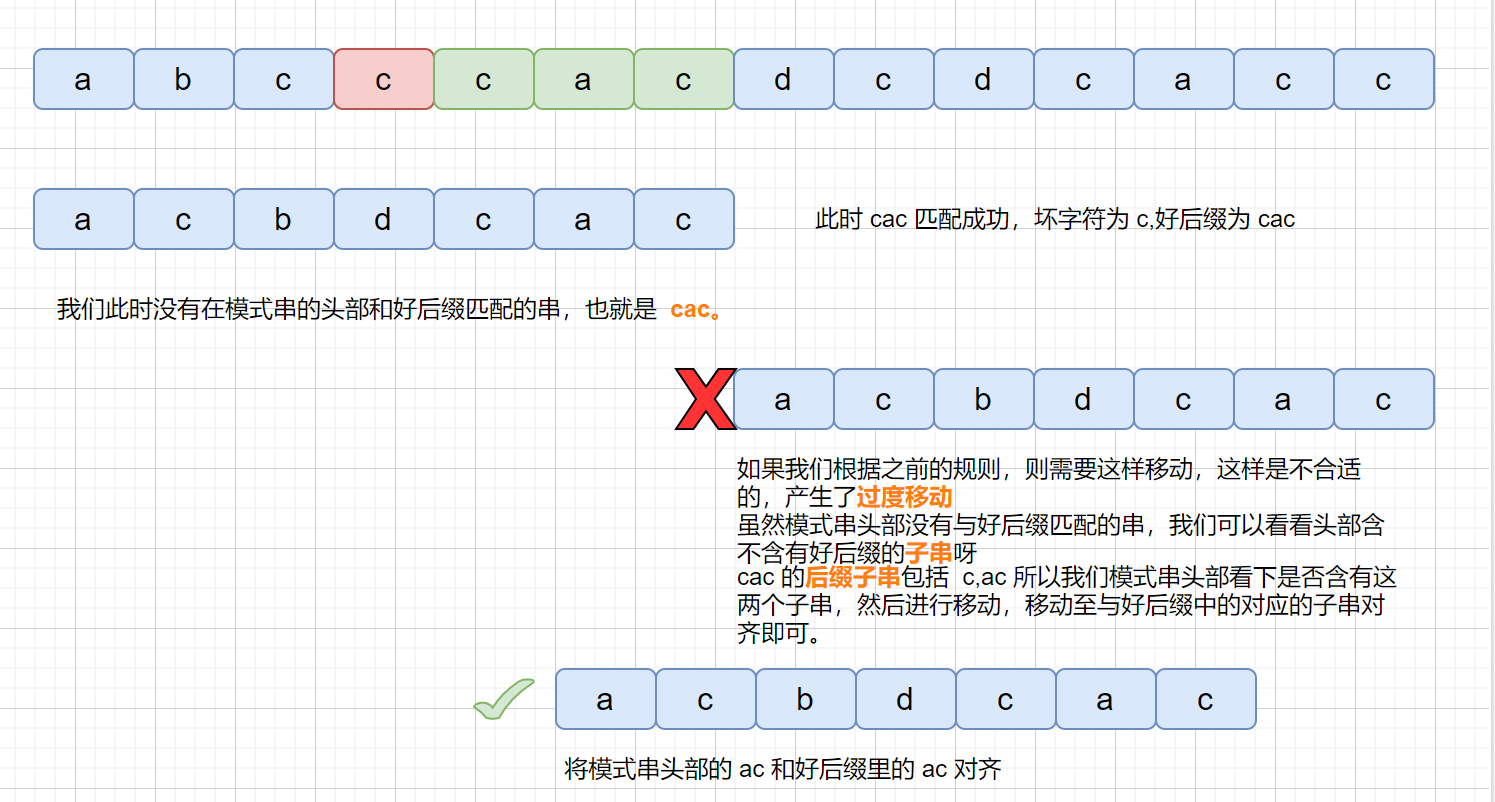
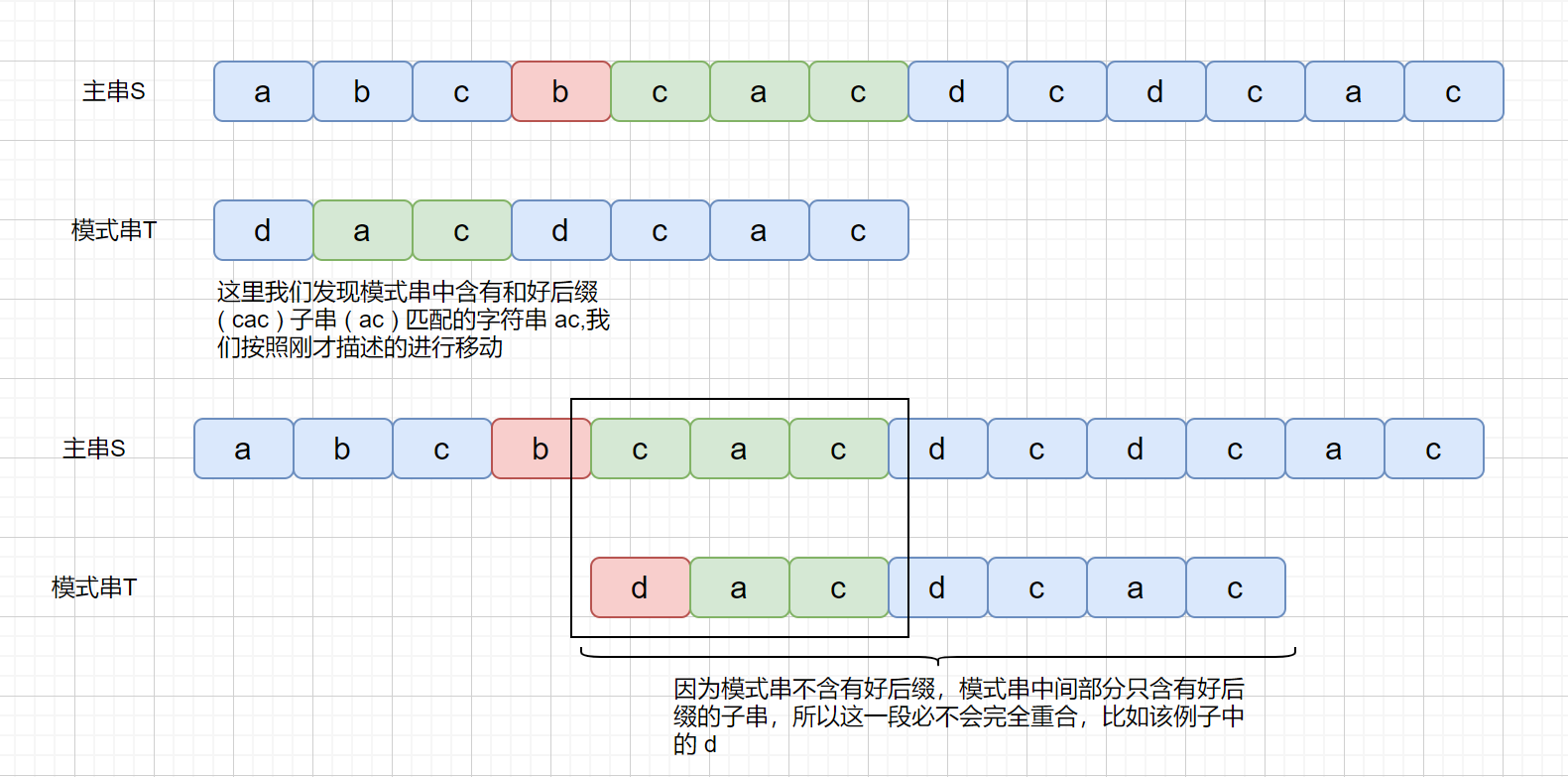
上面我们说到了，如果在模式串的**头部**没有发现好后缀，发现好后缀的子串也可以。但是为什么要强调这个头部呢？

我们下面来看一下这种情况

![不完全重合](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/不完全重合.6oayqd0dre00.png)

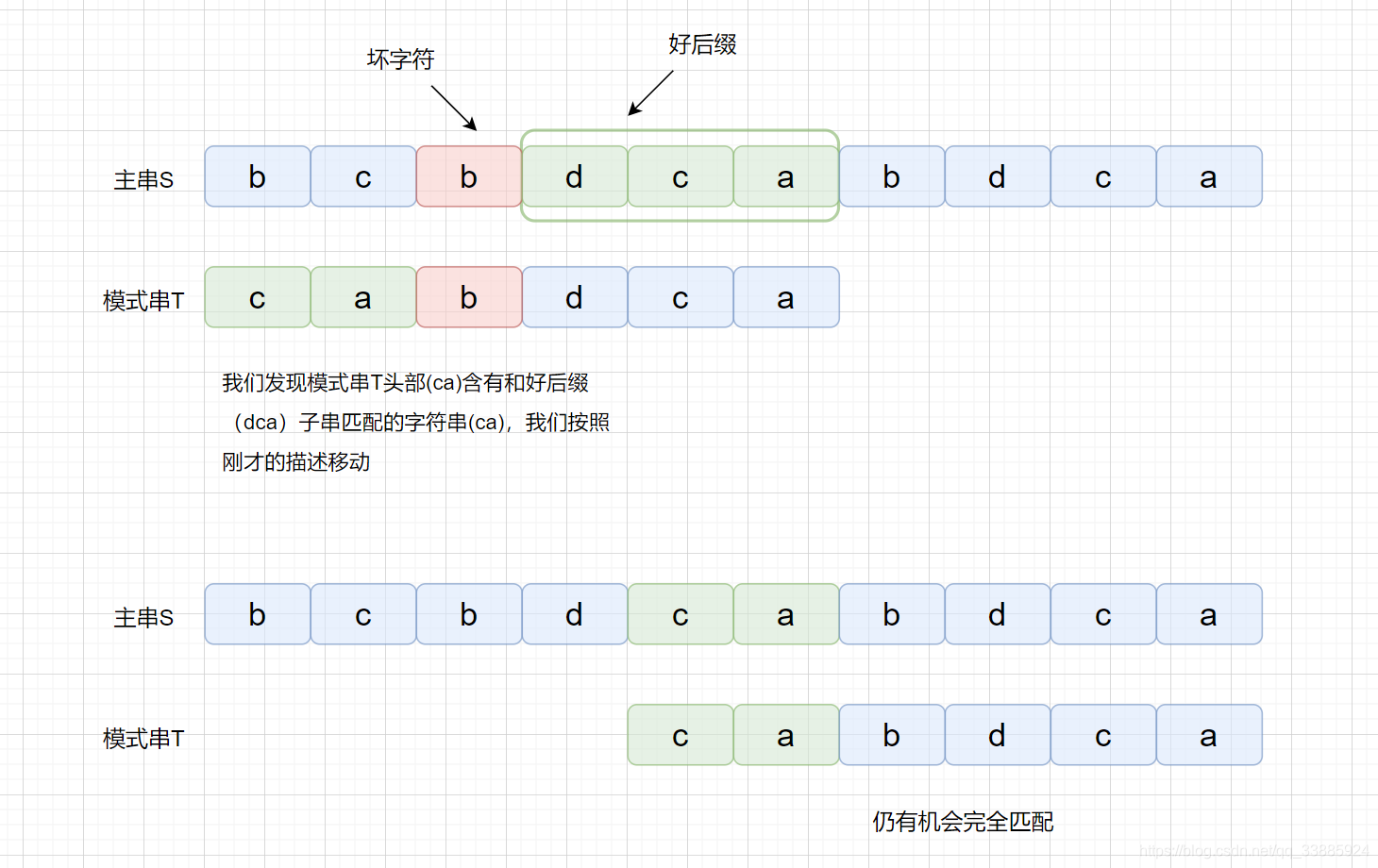
但是当我们在头部发现好后缀的子串时，是什么情况呢？

![](https://img-blog.csdnimg.cn/20210319204004219.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzMzODg1OTI0,size_16,color_FFFFFF,t_70#pic_center)

下面我们通过动图来看一下某一例子的具体的执行过程

![请添加图片描述](https://img-blog.csdnimg.cn/202103191939263.gif)

说到这里，坏字符和好后缀规则就算说完了，坏字符很容易理解，我们对好后缀总结一下

1.如果模式串**含有好后缀**，无论是中间还是头部可以按照规则进行移动。如果好后缀在模式串中出现多次，则以**最右侧的好后缀**为基准。

2.如果模式串**头部含有**好后缀子串则可以按照规则进行移动，中间部分含有好后缀子串则不可以。

3.如果在模式串尾部就出现不匹配的情况，即不存在好后缀时，则根据坏字符进行移动，这里有的文章没有提到，是个需要特别注意的地方，我是在这个论文里找到答案的，感兴趣的同学可以看下。

> Boyer R S，Moore J S. A fast string searching algorithm［J］. Communications of the ACM，1977，10： 762-772.

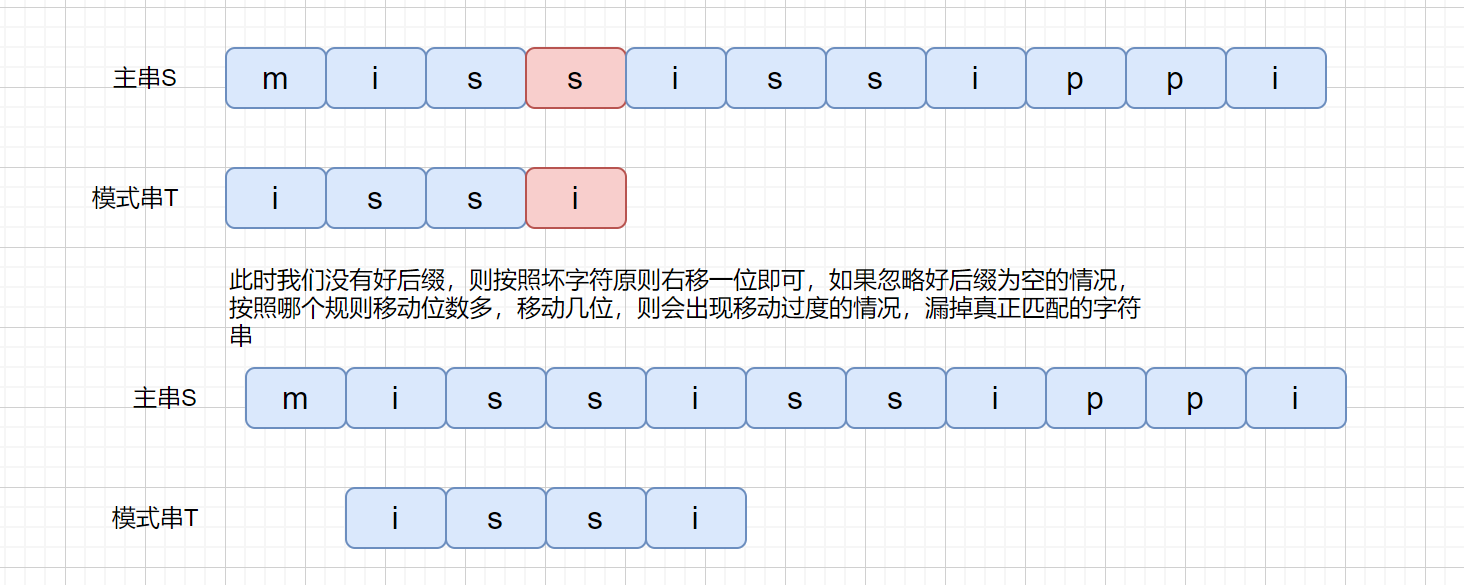
之前我们刚开始说坏字符的时候，是不是有可能会出现负值的情况，即往左移动的情况，所以我们为了解决这个问题，我们可以分别计算好后缀和坏字符往后滑动的位数**（好后缀不为 0 的情况）**，然后取两个数中最大的，作为模式串往后滑动的位数。

![五好后缀](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/五好后缀.6wvqxa4um040.png)

这破图画起来是真费劲啊。下面我们来看一下算法代码，代码有点长，我都标上了注释也在网站上 AC 了，如果各位感兴趣可以看一下，不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分

Java Code:

```java
class Solution {
    public int strStr(String haystack, String needle) {
        char[] hay = haystack.toCharArray();
        char[] need = needle.toCharArray();
        int haylen = haystack.length();
        int needlen = need.length;
        return bm(hay,haylen,need,needlen);
    }
    //用来求坏字符情况下移动位数
    private static void badChar(char[] b, int m, int[] bc) {
        //初始化
        for (int i = 0; i < 256; ++i) {
            bc[i] = -1;
        }
        //m 代表模式串的长度，如果有两个 a,则后面那个会覆盖前面那个
        for (int i = 0; i < m; ++i) {
            int ascii = (int)b[i];
            bc[ascii] = i;//下标
        }
    }
    //用来求好后缀条件下的移动位数
    private static void goodSuffix (char[] b, int m, int[] suffix,boolean[] prefix) {
        //初始化
        for (int i = 0; i < m; ++i) {
            suffix[i] = -1;
            prefix[i] = false;
        }
        for (int i = 0; i < m - 1; ++i) {
            int j = i;
            int k = 0;
            while (j >= 0 && b[j] == b[m-1-k]) {
                --j;
                ++k;
                suffix[k] = j + 1;
            }
            if (j == -1) prefix[k] = true;
        }
    }
    public static int bm (char[] a, int n, char[] b, int m) {

        int[] bc = new int[256];//创建一个数组用来保存最右边字符的下标
        badChar(b,m,bc);
        //用来保存各种长度好后缀的最右位置的数组
        int[] suffix_index = new int[m];
        //判断是否是头部，如果是头部则true
        boolean[] ispre = new boolean[m];
        goodSuffix(b,m,suffix_index,ispre);
        int i = 0;//第一个匹配字符
        //注意结束条件
        while (i <= n-m) {
            int j;
            //从后往前匹配，匹配失败，找到坏字符
            for (j = m - 1; j >= 0; --j) {
                if (a[i+j] != b[j]) break;
            }
            //模式串遍历完毕，匹配成功
            if (j < 0) {
                return i;
            }
            //下面为匹配失败时，如何处理
            //求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
            int x = j - bc[(int)a[i+j]];
            int y = 0;
            //好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
            if (y < m-1 && m - 1 - j > 0) {
                y = move(j, m, suffix_index,ispre);
            }
            //移动
            i = i + Math.max(x,y);

        }
        return -1;
    }
    // j代表坏字符的下标
    private static int move (int j, int m, int[] suffix_index, boolean[] ispre) {
        //好后缀长度
        int k = m - 1 - j;
        //如果含有长度为 k 的好后缀，返回移动位数，
        if (suffix_index[k] != -1) return j - suffix_index[k] + 1;
        //找头部为好后缀子串的最大长度，从长度最大的子串开始
        for (int r = j + 2; r <= m-1; ++r) {
            //如果是头部
            if (ispre[m-r] == true) {
                return r;
            }
        }
        //如果没有发现好后缀匹配的串，或者头部为好后缀子串，则移动到 m 位，也就是匹配串的长度
        return m;
    }
}
```

Python Code:

```python
from typing import List
class Solution:
    def strStr(self, haystack: str, needle: str)->int:
        haylen = len(haystack)
        needlen = len(needle)
        return self.bm(haystack, haylen, needle, needlen)

    # 用来求坏字符情况下移动位数
    def badChar(self, b: str, m: int, bc: List[int]):
        # 初始化
        for i in range(0, 256):
            bc[i] = -1
        # m 代表模式串的长度，如果有两个 a，则后面那个会覆盖前面那个
        for i in range(0, m,):
            ascii = ord(b[i])
            bc[ascii] = i# 下标

    # 用来求好后缀条件下的移动位数
    def goodSuffix(self, b: str, m: int, suffix: List[int], prefix: List[bool]):
        # 初始化
        for i in range(0, m):
            suffix[i] = -1
            prefix[i] = False
        for i in range(0, m - 1):
            j = i
            k = 0
            while j >= 0 and b[j] == b[m - 1 - k]:
                j -= 1
                k += 1
                suffix[k] = j + 1
            if j == -1:
                prefix[k] = True

    def bm(self, a: str, n: int, b: str, m: int)->int:
        bc = [0] * 256# 创建一个数组用来保存最右边字符的下标
        self.badChar(b, m, bc)
        # 用来保存各种长度好后缀的最右位置的数组
        suffix_index = [0] * m
        # 判断是否是头部，如果是头部则True
        ispre = [False] * m
        self.goodSuffix(b, m, suffix_index, ispre)
        i = 0# 第一个匹配字符
        # 注意结束条件
        while i <= n - m:
            # 从后往前匹配，匹配失败，找到坏字符
            j = m - 1
            while j >= 0:
                if a[i + j] != b[j]:
                    break
                j -= 1
            # 模式串遍历完毕，匹配成功
            if j < 0:
                return i
            # 下面为匹配失败时，如何处理
            # 求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
            x = j - bc[ord(a[i + j])]
            y = 0
            # 好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
            if y < m - 1 and m - 1 - j > 0:
                y = self.move(j, m, suffix_index, ispre)
            # 移动
            i += max(x, y)
        return -1

    # j代表坏字符的下标
    def move(j: int, m: int, suffix_index: List[int], ispre: List[bool])->int:
        # 好后缀长度
        k = m - 1 - j
        # 如果含有长度为 k 的好后缀，返回移动位数
        if suffix_index[k] != -1:
            return j - suffix_index[k] + 1
        # 找头部为好后缀子串的最大长度，从长度最大的子串开始
        for r in range(j + 2, m):
            # //如果是头部
            if ispre[m - r] == True:
                return r
        # 如果没有发现好后缀匹配的串，或者头部为好后缀子串，则移动到 m 位，也就是匹配串的长度
        return m
```

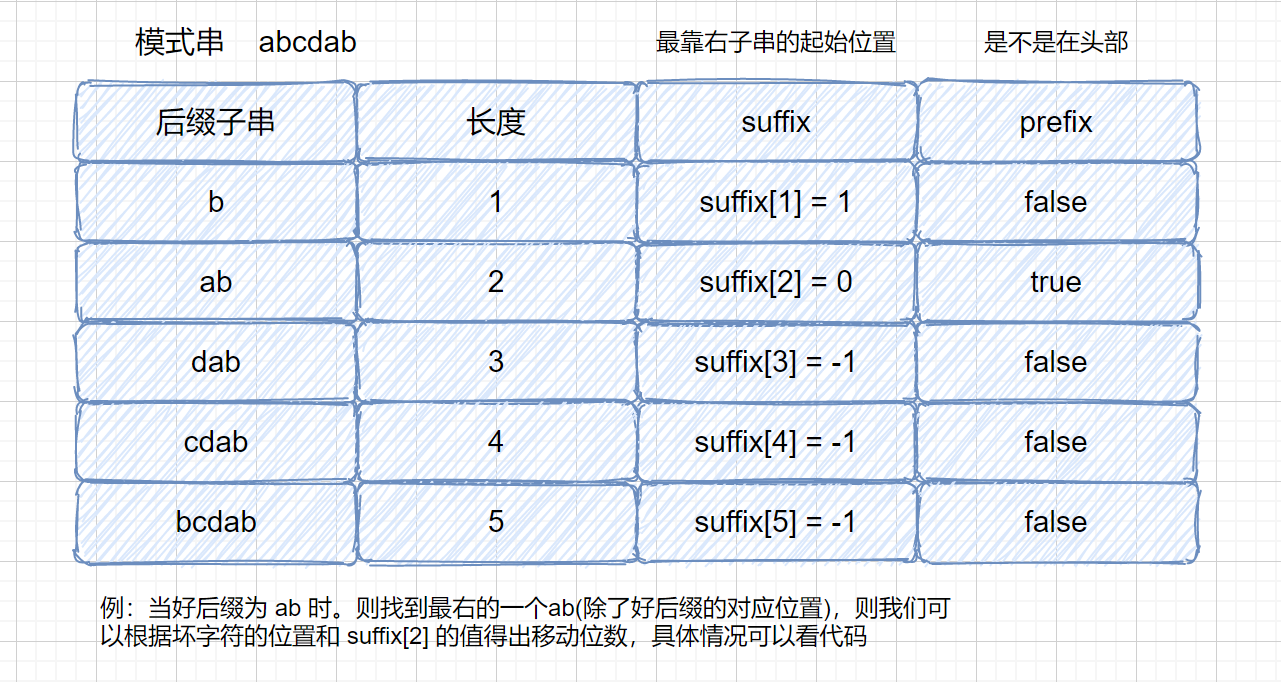
我们来理解一下我们代码中用到的两个数组，因为两个规则的移动位数，只与模式串有关，与主串无关，所以我们可以提前求出每种情况的移动情况，保存到数组中。

![头缀函数](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/头缀函数.145da63ig3s0.png)