添加了python版本代码

为数据结构和算法文件夹下的代码增加了python语言版本

animation-simulation/数据结构和算法/BM.md

@@ -122,6 +122,8 @@ BM 算法是从右往左进行比较，发现坏字符的时候此时 cac  已
 
 这破图画起来是真费劲啊。下面我们来看一下算法代码，代码有点长，我都标上了注释也在网站上 AC 了，如果各位感兴趣可以看一下，不感兴趣理解坏字符和好后缀规则即可。可以直接跳到 KMP 部分
 
+Java Code:
+
 ```java
 class Solution {
     public int strStr(String haystack, String needle) {
@@ -215,6 +217,89 @@ class Solution {
 }
 ```
 
+Python Code:
+
+```python
+from typing import List
+class Solution:
+    def strStr(self, haystack: str, needle: str)->int:
+        haylen = len(haystack)
+        needlen = len(needle)
+        return self.bm(haystack, haylen, needle, needlen)
+    
+    # 用来求坏字符情况下移动位数
+    def badChar(self, b: str, m: int, bc: List[int]):
+        # 初始化
+        for i in range(0, 256):
+            bc[i] = -1
+        # m 代表模式串的长度，如果有两个 a，则后面那个会覆盖前面那个
+        for i in range(0, m,):
+            ascii = ord(b[i])
+            bc[ascii] = i# 下标
+    
+    # 用来求好后缀条件下的移动位数
+    def goodSuffix(self, b: str, m: int, suffix: List[int], prefix: List[bool]):
+        # 初始化
+        for i in range(0, m):
+            suffix[i] = -1
+            prefix[i] = False
+        for i in range(0, m - 1):
+            j = i
+            k = 0
+            while j >= 0 and b[j] == b[m - 1 - k]:
+                j -= 1
+                k += 1
+                suffix[k] = j + 1
+            if j == -1:
+                prefix[k] = True
+    
+    def bm(self, a: str, n: int, b: str, m: int)->int:
+        bc = [0] * 256# 创建一个数组用来保存最右边字符的下标
+        self.badChar(b, m, bc)
+        # 用来保存各种长度好后缀的最右位置的数组
+        suffix_index = [0] * m
+        # 判断是否是头部，如果是头部则True
+        ispre = [False] * m
+        self.goodSuffix(b, m, suffix_index, ispre)
+        i = 0# 第一个匹配字符
+        # 注意结束条件
+        while i <= n - m:
+            # 从后往前匹配，匹配失败，找到坏字符
+            j = m - 1
+            while j >= 0:
+                if a[i + j] != b[j]:
+                    break
+                j -= 1
+            # 模式串遍历完毕，匹配成功
+            if j < 0:
+                return i
+            # 下面为匹配失败时，如何处理
+            # 求出坏字符规则下移动的位数，就是我们坏字符下标减最右边的下标
+            x = j - bc[ord(a[i + j])]
+            y = 0
+            # 好后缀情况，求出好后缀情况下的移动位数,如果不含有好后缀的话，则按照坏字符来
+            if y < m - 1 and m - 1 - j > 0:
+                y = self.move(j, m, suffix_index, ispre)
+            # 移动
+            i += max(x, y)
+        return -1
+    
+    # j代表坏字符的下标
+    def move(j: int, m: int, suffix_index: List[int], ispre: List[bool])->int:
+        # 好后缀长度
+        k = m - 1 - j
+        # 如果含有长度为 k 的好后缀，返回移动位数
+        if suffix_index[k] != -1:
+            return j - suffix_index[k] + 1
+        # 找头部为好后缀子串的最大长度，从长度最大的子串开始
+        for r in range(j + 2, m):
+            # //如果是头部
+            if ispre[m - r] == True:
+                return r
+        # 如果没有发现好后缀匹配的串，或者头部为好后缀子串，则移动到 m 位，也就是匹配串的长度
+        return m
+```
+
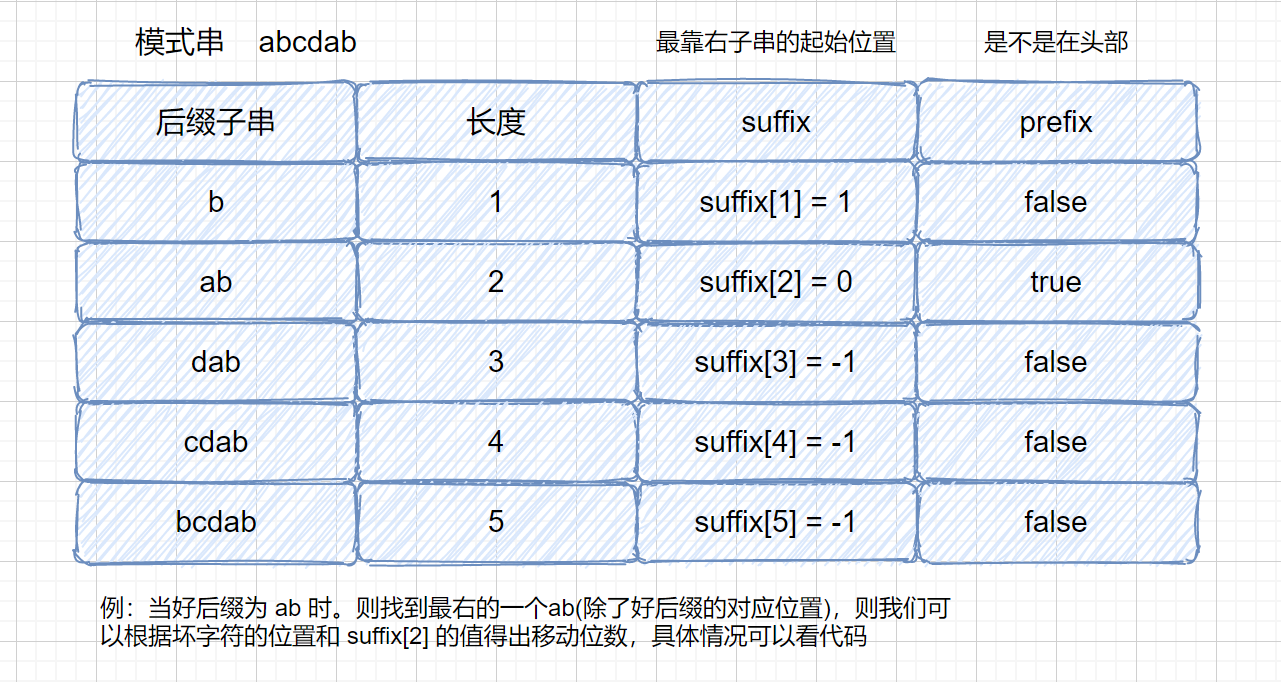
 我们来理解一下我们代码中用到的两个数组，因为两个规则的移动位数，只与模式串有关，与主串无关，所以我们可以提前求出每种情况的移动情况，保存到数组中。
 
 ![头缀函数](https://cdn.jsdelivr.net/gh/tan45du/photobed@master/photo/头缀函数.145da63ig3s0.png)