mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2026-02-25 21:39:55 +00:00
希尔
This commit is contained in:
@@ -6,11 +6,11 @@
|
||||
|
||||
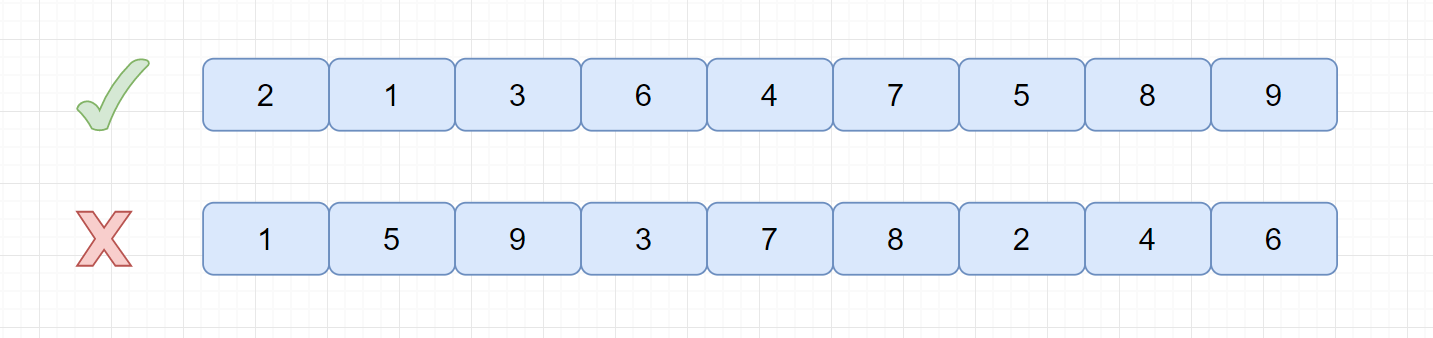
基本有序:就是小的关键字基本在前面,大的关键字基本在后面,不大不小的基本在中间。见下图。
|
||||
|
||||
|
||||

|
||||
|
||||
我们已经了解了希尔排序的基本思想,下面我们通过一个绘图来描述下其执行步骤。
|
||||
|
||||
.1oixbv11eork.png)
|
||||

|
||||
|
||||
先逐步分组进行粗调,在进行直接插入排序的思想就是希尔排序。我们刚才的分组跨度(4,2,1)被称为希尔排序的增量,我们上面用到的是逐步折半的增量方法,这也是在发明希尔排序时提出的一种朴素方法,被称为希尔增量,
|
||||
|
||||
|
||||
84
gif-algorithm/数组篇/leetcode1两数之和.md
Normal file
84
gif-algorithm/数组篇/leetcode1两数之和.md
Normal file
@@ -0,0 +1,84 @@
|
||||
### leetcode 1:两数之和
|
||||
|
||||
**题目描述:**
|
||||
|
||||
> 给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
|
||||
>
|
||||
> 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
|
||||
|
||||
**示例:**
|
||||
|
||||
> 给定 nums = [2, 7, 11, 15], target = 9
|
||||
>
|
||||
> 因为 nums[0] + nums[1] = 2 + 7 = 9
|
||||
> 所以返回 [0, 1]
|
||||
|
||||
题目很容易理解,即让查看数组中有没有两个数的和为目标数,如果有的话则返回两数下标,我们为大家提供两种解法双指针(暴力)法,和哈希表法
|
||||
|
||||
**双指针(暴力)法**
|
||||
|
||||
**解析**
|
||||
|
||||
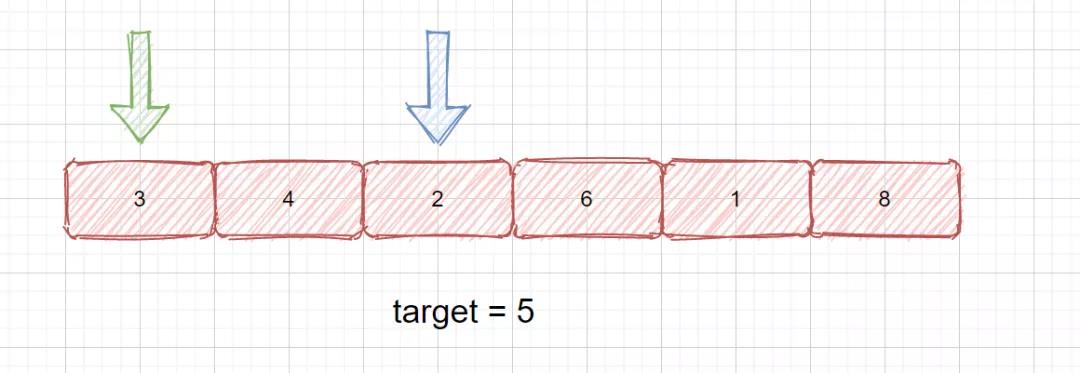
双指针(L,R)法的思路很简单,L指针用来指向第一个值,R指针用来从第L指针的后面查找数组中是否含有和L指针指向值和为目标值的数。见下图
|
||||
|
||||
|
||||
|
||||
例:绿指针指向的值为3,蓝指针需要在绿指针的后面遍历查找是否含有 target - 3 = 2的元素,若含有返回即可。
|
||||
|
||||
**题目代码**
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int[] twoSum(int[] nums, int target) {
|
||||
if(nums.length < 2){
|
||||
return new int[0];
|
||||
}
|
||||
int[] rearr = new int[2];
|
||||
//查询元素
|
||||
for(int i = 0; i < nums.length; i++){
|
||||
for(int j = i+1; j < nums.length; j++ ){
|
||||
//发现符合条件情况
|
||||
if(nums[i] + nums[j] ==target){
|
||||
rearr[0] = i;
|
||||
rearr[1] = j;
|
||||
}
|
||||
}
|
||||
}
|
||||
return rearr;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**哈希表**
|
||||
|
||||
**解析**
|
||||
|
||||
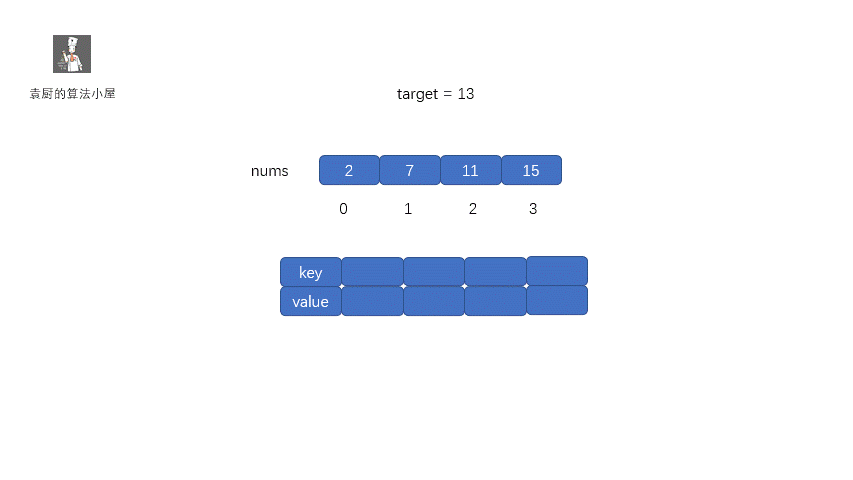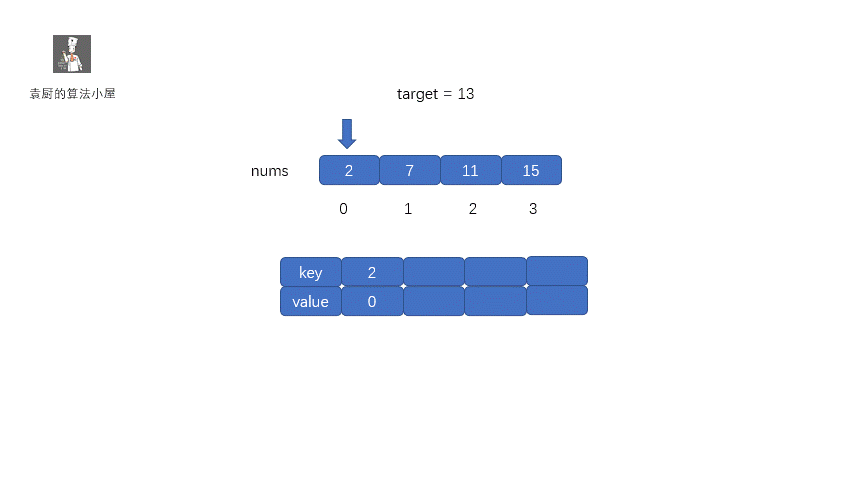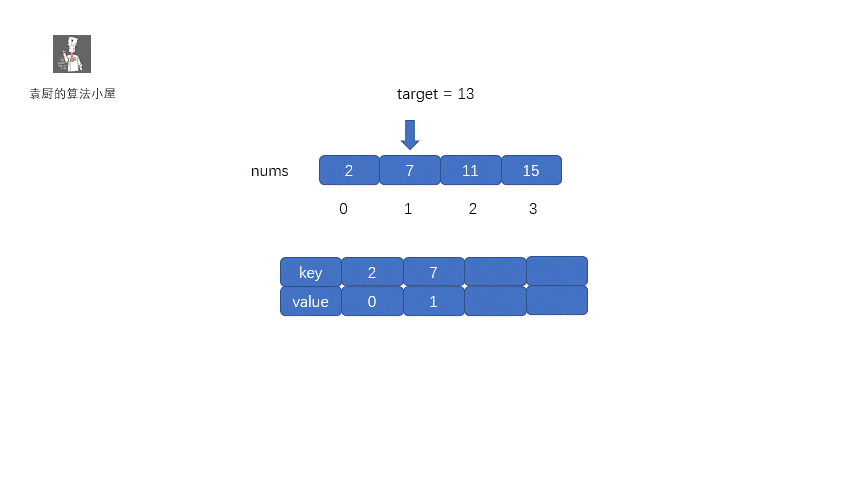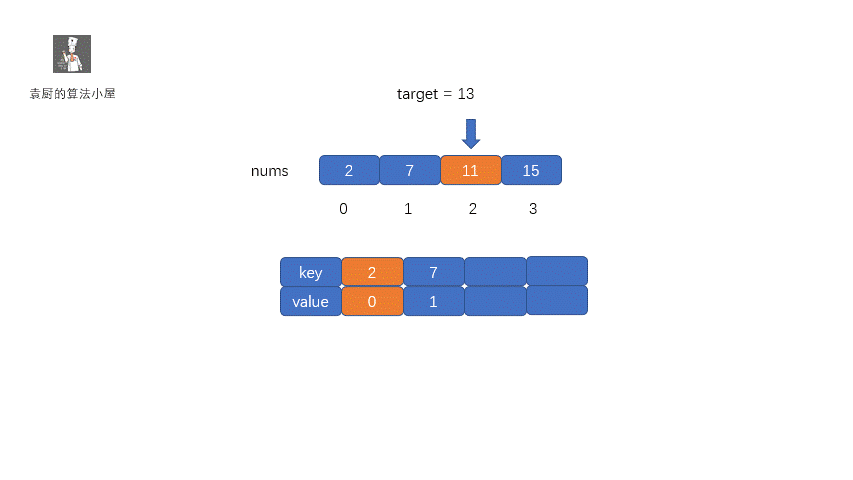
哈希表的做法很容易理解,我们只需通过一次循环即可,假如我们的 target 值为 9,当前指针指向的值为 2 ,我们只需从哈希表中查找是否含有 7,因为9 - 2 =7 。如果含有 7 我们直接返回即可,如果不含有则将当前的2存入哈希表中,指针移动,指向下一元素。注: key 为元素值,value 为元素索引。
|
||||
|
||||
**动图解析:**
|
||||
|
||||
|
||||
|
||||
是不是很容易理解,下面我们来看一下题目代码。
|
||||
|
||||
**题目代码:**
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int[] twoSum(int[] nums, int target) {
|
||||
HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
|
||||
for(int i = 0; i < nums.length; i++){
|
||||
//如果存在则返回
|
||||
if(map.containsKey(target-nums[i])){
|
||||
return new int[]{map.get(target-nums[i]),i};
|
||||
}
|
||||
//不存在则存入
|
||||
map.put(nums[i],i);
|
||||
|
||||
}
|
||||
return new int[0];
|
||||
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Reference in New Issue
Block a user