次数

README.md

@@ -1,4 +1,7 @@
 # algorithm-base
-专门为初学者的准备的基地，没有最细只有更细！
+专门为初学者的准备的算法基地，没有最细只有更细！
 
 立志用动画将晦涩难懂的算法描述的通俗易懂。
+
+热烈欢迎你的批评指正，但是不接受骂人。感谢支持
+

gif-algorithm/求次数问题/只出现一次的数.md

@@ -0,0 +1,231 @@
+## 只出现一次的数
+
+> 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
+
+示例 1:
+
+> 输入: [2,2,1]
+> 输出: 1
+
+示例 2:
+
+> 输入: [4,1,2,1,2]
+> 输出: 4
+
+这个题目非常容易理解，就是让我们找出那个只出现一次的数字，那么下面我们来看一下这几种解题方法吧
+
+### HashMap
+
+#### 解析
+
+用 HashMap 的这个方法是很容易实现的，题目要求不是让我们求次数嘛，那我们直接遍历数组将每个数字和其出现的次数存到 哈希表里 就可以了，然后我们再从哈希表里找出出现一次的那个数返回即可。
+
+![哈希表解法](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/哈希表解法.1kefww8xsig0.png)
+
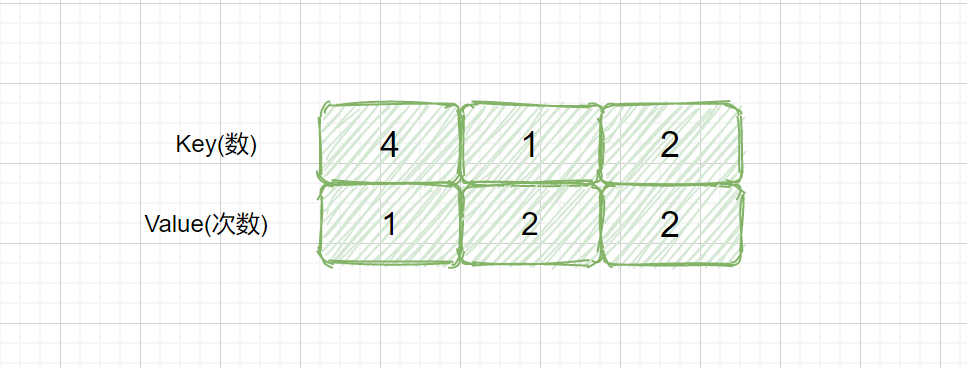
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+        //特殊情况
+        if (nums.length == 1) {
+            return nums[0];
+        }
+        //HashMap
+        HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
+        //将其存入哈希表中，含义为，若该元素不存在则存入表中，并计数为1，若已经存在获取次数并加1.
+        for (int x : nums) {
+            map.put(x , map.getOrDefault(x,0) + 1);
+        }
+        //遍历出出现次数为1的情况
+        for (int y : map.keySet()) {
+            if(map.get(y) == 1){
+                return y;
+            }
+        }    
+        return 0;
+
+    }
+}
+```
+
+### 排序搜索法
+
+#### 解析
+
+这个方法也是特别容易想到的，我们首先对数组进行排序，然后遍历数组，因为数组中其他数字都出现两次，只有目标值出现一次，所以则让我们的指针每次跳两步，当发现当前值和前一位不一样的情况时，返回前一位即可，当然我们需要考虑这种情况，当我们的目标值出现在数组最后一位的情况，所以当数组遍历结束后没有返回值，则我们需要返回数组最后一位，下面我们看一下动图解析。
+
+![排序](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/排序.6sp72k3iaqw0.gif)
+
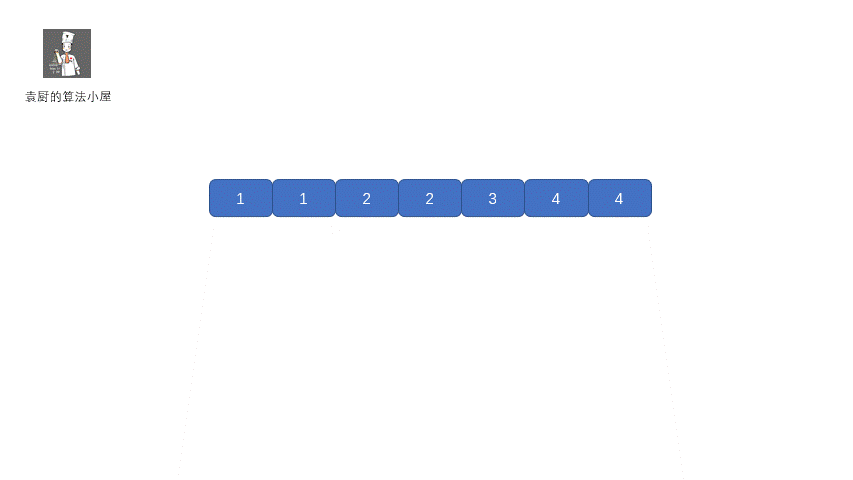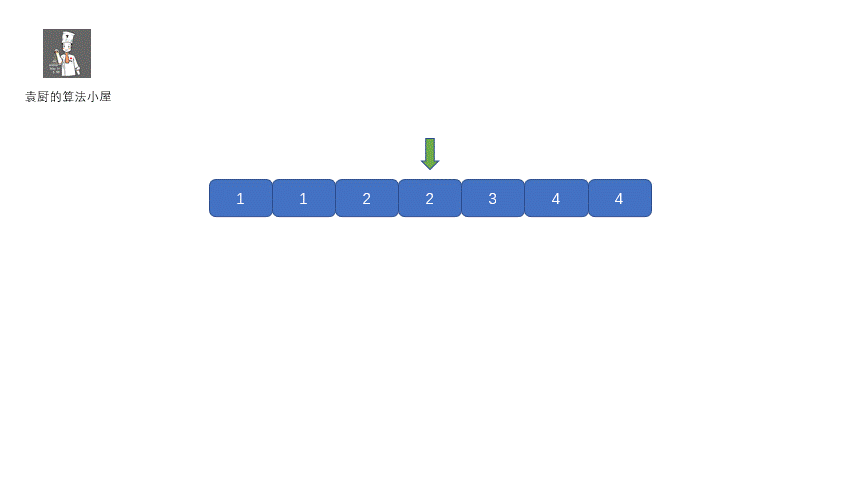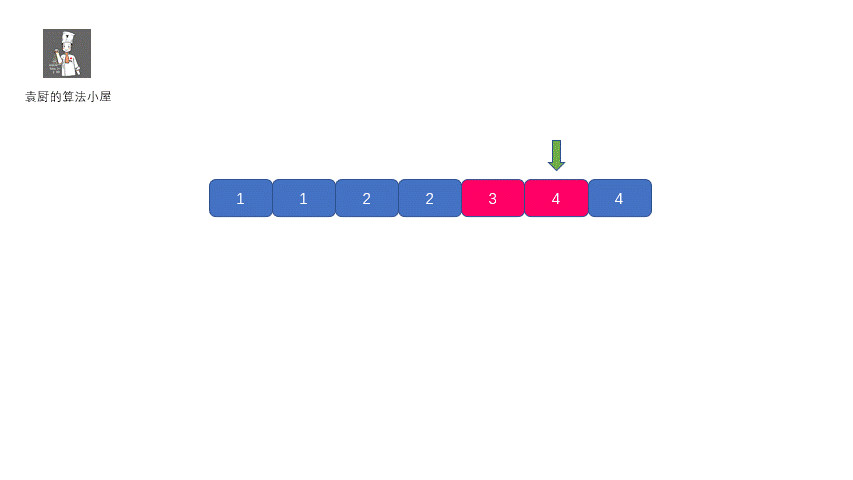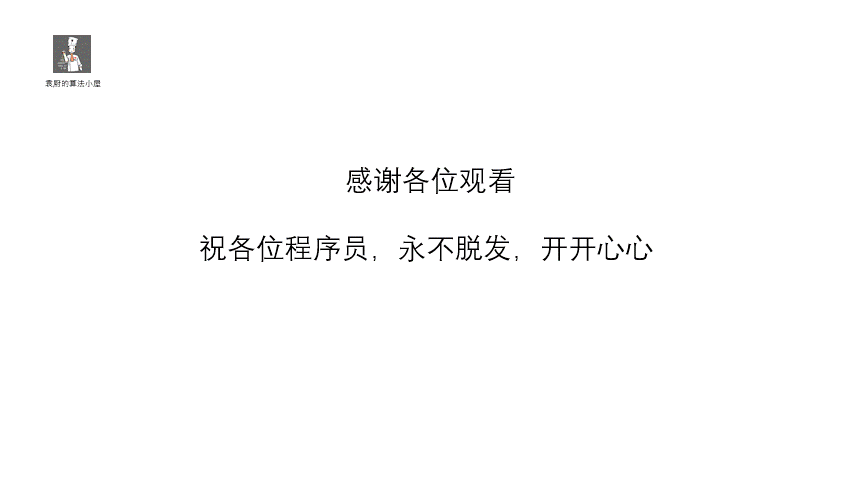
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+        if (nums.length == 1){
+            return nums[0];
+        }
+        //排序
+        Arrays.sort(nums);
+        for (int i = 1; i < nums.length-1; i+=2){
+            if (nums[i] == nums[i-1]){
+                continue;
+            }else{
+                return nums[i-1];
+            }
+        }
+        return nums[nums.length-1];
+
+    }
+}
+```
+
+
+
+### HashSet
+
+#### 解析
+
+这个方法也是比较容易实现的，我们利用 HashSet 来完成。HashSet 在我们刷题时出现频率是特别高的，它是基于 HashMap 来实现的，是一个不允许有重复元素的集合。那么在这个题解中，它起到什么作用呢？解题思路如下，我们依次遍历元素并与 HashSet 内的元素进行比较，如果 HashSet 内没有该元素（说明该元素第一次出现）则存入，若是 HashSet 已经存在该元素(第二次出现)，则将其从 HashSet 中去除，并继续遍历下一个元素。最后 HashSet 内剩下的则为我们的目标数。思路和我们之前说过的括号匹配问题类似，我们一起来看一下动图解析吧。
+
+![HashSet](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/HashSet.4b6dcxwj07c0.gif)
+
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+         if (nums.length == 1){
+             return nums[0];
+         }
+         HashSet<Integer> set = new HashSet<>();
+         //循环遍历
+         for (int x : nums){
+             //已经存在，则去除
+             if(set.contains(x)){
+                 set.remove(x);
+             }
+             //否则存入
+             else{
+                 set.add(x);
+             }
+         }
+         //返回仅剩的一个元素
+         return set.iterator().next();
+    }
+}
+```
+
+
+
+### 栈
+
+#### 解析
+
+该方法也很容易想到，我们首先将其排序，然后遍历数组，如果栈为空则将当前元素压入栈，如果栈不为空，若当前元素和栈顶元素相同则出栈，继续遍历下一元素，如果当前元素和栈顶元素不同的话，则说明栈顶元素是只出现一次的元素，我们将其返回即可。这个题目也可以使用队列做，思路一致，我们就不在这里说明啦。下面我们看下动图解析。
+
+![栈](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/栈.6mzstgebww00.gif)
+
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+        if (nums.length == 1) {
+            return nums[0];
+        }
+        Arrays.sort(nums);
+        Stack<Integer> stack = new Stack<>();
+        for (int x : nums){
+           if (stack.isEmpty()) {
+               stack.push(x);
+               continue;
+           }
+            //不同时直接跳出
+           if (stack.peek() != x) {
+               break;
+           }
+            //相同时出栈
+           stack.pop();           
+        }
+        return stack.peek();
+    }
+}
+```
+
+
+
+### 求和法
+
+#### 解析
+
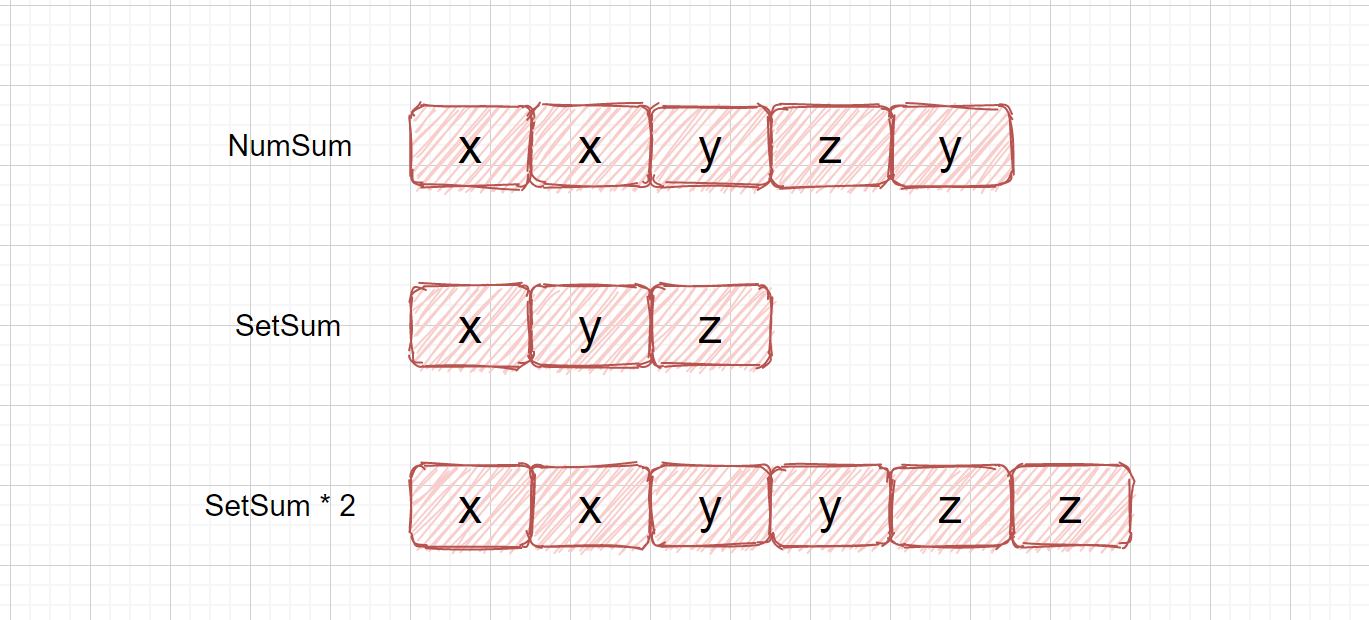
+这个方法也比较简单，也是借助咱们的 HashSet ，具体思路如下，我们通过 HashSet 保存数组内的元素，然后进行求和（setsum），那么得到的这个和则为去除掉重复元素的和，我们也可以得到所有元素和（numsum）。因为我们其他元素都出现两次，仅有一个元素出现一次，那我们通过 setsum * 2 - numsum 得到的元素则为出现一次的数。
+
+![求和解法](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/求和解法.2tds49a3vzq0.png)
+
+上面我们的 SetSum  * 2 - NumSum = z 也就是我们所求的值， 是不是感觉很简单呀。
+
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+       if (nums.length == 1){
+           return nums[0];
+       }
+       HashSet<Integer> set = new HashSet<>();
+       int setsum = 0;
+       int numsum = 0;
+       for (int x : nums) {
+           //所有元素的和
+           numsum += x; 
+           if (!set.contains(x)) {
+               //HashSet内元素的和
+               setsum += x; 
+           }
+           set.add(x);
+       } 
+       //返回值
+       return setsum * 2 - numsum;
+    }
+}
+```
+
+
+
+### 位运算
+
+#### 解析
+
+这个方法主要是借助咱们的位运算符 ^ 按位异或，我们先来了解一下这个位运算符。
+
+> 按位异或(XOR)运算符“^”是双目运算符。 其功能是参与运算的两数各对应的二进位相异或，当两对应的二进位相异时，结果为1。相同时为0。
+
+> 任何数和0异或，仍为本身：a⊕0 = a
+> 任何数和本身异或，为0：a⊕a = 0
+> 异或运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
+
+例：
+
+![异或运算](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/异或运算.1myeo11xgqo0.png)
+
+我们通过上面的例子了解了异或运算，对应位相异时得 1，相同时得 0，那么某个数跟本身异或时，因为对应位都相同所以结果为 0 ， 然后异或又满足交换律和结合律。则
+
+![image-20201129120648802](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/image-20201129120648802.2ajgng6zzd7o.png)
+
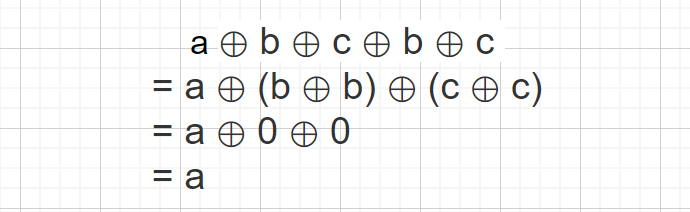
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+        int num = 0;
+        //异或
+        for (int x : nums) {    
+              num ^= x;
+        }
+        return num;
+    }
+}
+```
+
+本题一共介绍了6种解题方法，肯定还有别的方法，欢迎大家讨论。大家可以在做题的时候一题多解。这样能大大提高自己解题能力。下面我们来看一下这些方法如何应用到其他题目上。

gif-algorithm/求次数问题/只出现一次的数2.md

@@ -0,0 +1,109 @@
+## 只出现一次的数Ⅱ
+
+> 给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。
+
+示例 1:
+
+> 输入: [2,2,3,2]
+> 输出: 3
+
+示例 2:
+
+> 输入: [0,1,0,1,0,1,99]
+> 输出: 99
+
+题目很容易理解，刚才的题目是其他元素出现两次，目标元素出现一次，该题是其他元素出现三次，目标元素出现一次，所以我们完全可以借助上题的一些做法解决该题。
+
+### 求和法
+
+#### 解析
+
+我们在上题中介绍了求和法的解题步骤，现在该题中其他元素都出现三次，我们的目标元素出现一次，所以我们利用求和法也是完全 OK 的。下面我们来看具体步骤吧。
+
+1.通过遍历数组获取所有元素的和以及 HashSet 内元素的和。
+
+2.（SumSet  *  3  -  SumNum）/ 2即可，除以 2 是因为我们减去之后得到的是 2 倍的目标元素。
+
+注：这个题目中需要注意溢出的情况 。
+
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+        HashSet<Integer> set = new HashSet<>();
+        long sumset = 0;
+        long sumnum = 0; 
+        for (int x : nums) {
+            //所有元素的和
+            sumnum += x;
+            if (set.contains(x)) {
+                continue;               
+            }  
+            //HashSet元素和
+            sumset += x;
+            set.add(x);
+        }
+        //返回只出现一次的数
+        return (int)((3 * sumset - sumnum) / 2);
+    }
+}
+```
+
+这个题目用 HashMap 和排序查找肯定也是可以的，大家可以自己写一下，另外我们在第一题中有个利用异或求解的方法，但是这个题目是出现三次，我们则不能利用直接异或来求解，那还有其他方法吗？
+
+### 位运算
+
+#### 解析
+
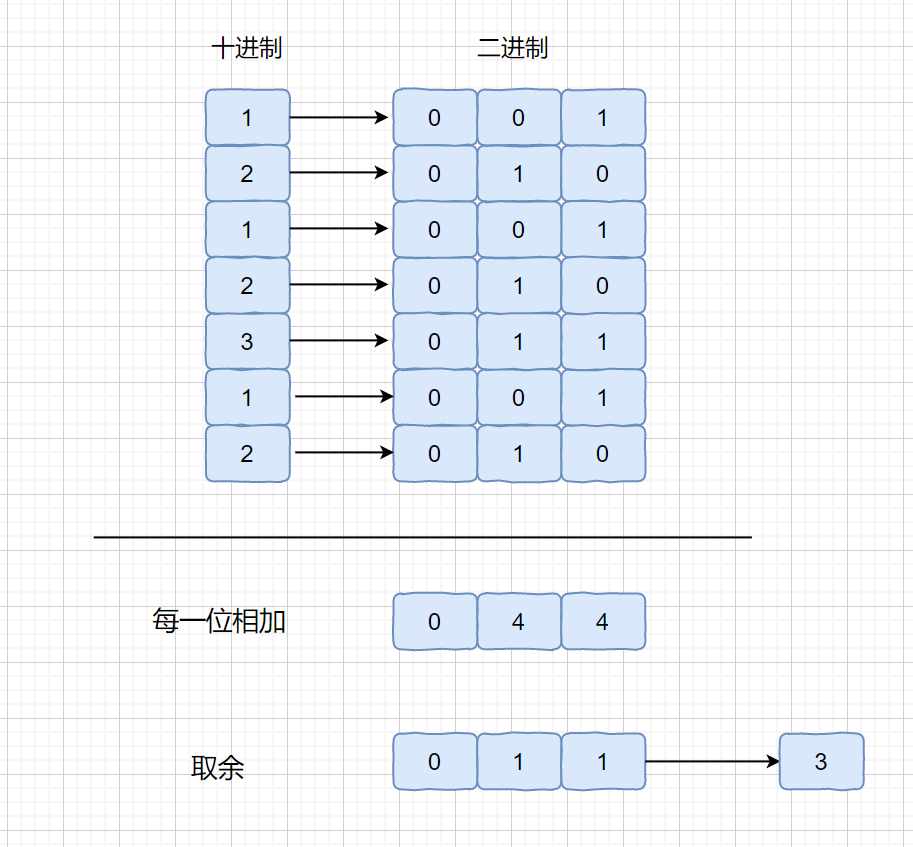
+这个方法主要做法是将我们的数的二进制位每一位相加，然后对其每一位的和取余 ，我们看下面的例子。
+
+![只出现一次的数字2](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/只出现一次的数字2.5p4wxbiegxc0.png)
+
+那么我们为什么要这样做呢？大家想一下，如果其他数都出现 3 次，只有目标数出现 1 次，那么每一位的 1 的个数无非有这2种情况，为 3 的倍数（全为出现三次的数） 或 3 的倍数 +1（包含出现一次的数）。这个 3 的倍数 +1 的情况也就是我们的目标数的那一位。
+
+#### 题目代码
+
+```java
+class Solution {
+    public int singleNumber(int[] nums) {
+      int res = 0;
+      for(int i = 0; i < 32; i++){
+          int count = 0;
+          for (int j = 0; j < nums.length; j++) {
+              //先将数右移，并求出最后一位为 1 的个数
+              if ((nums[j] >> i & 1) == 1) {
+                  count++;
+              }             
+          }
+          //找到某一位取余为 1 的数，并左移，为了将这一位循环结束后移至原位
+          if (count % 3 != 0) {
+              res = res | 1 << i;
+          }
+      }
+      return res;       
+    }
+}
+```
+
+我们来解析一下我们的代码
+
+> **<<**     左移动运算符：运算数的各二进位全部左移若干位，由  **<<**  右边的数字指定了移动的位数，高位丢弃，低位补0。
+>
+> **>>**     右移动运算符：把">>"左边的运算数的各二进位全部右移若干位，**>>** 右边的数字指定了移动的位数
+
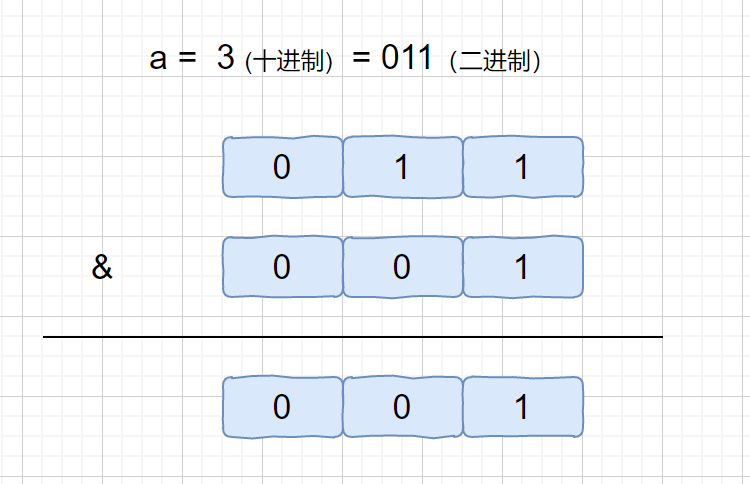
+另外我们的代码中还包含了 a & 1  和  a | 1 这有什么作用呢？继续看下图
+
+> **&**       按位与运算符：参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0
+
+
+
+![只出现一次的数位运算且](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/只出现一次的数位运算且.vq3lcgv0rbk.png)
+
+因为我们 a & 1 中 1 只有最后一位为 1，其余位皆为 0 ，所以我们发现 a & 1的作用就是判断 a 的最后一位是否为 1 ，如果 a 的最后一位为 1 ，a & 1 = 1,否则为 0 。所以我们还可以通过这个公式来判断 a 的奇偶性。
+
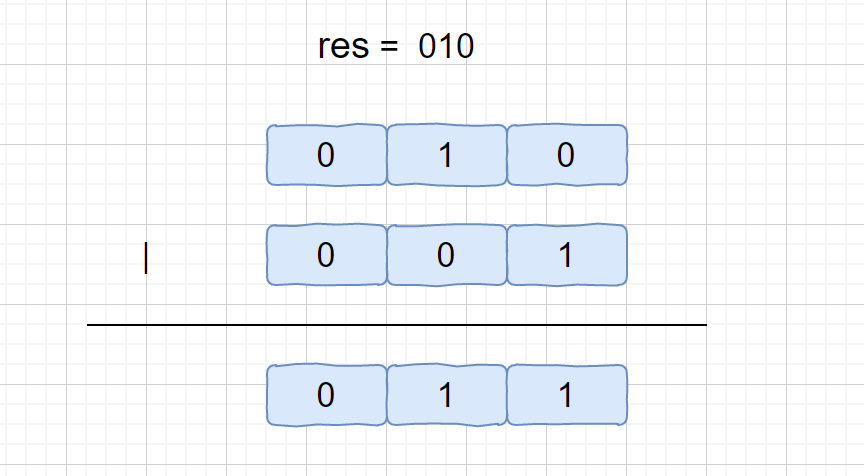
+> **|**        按位或运算符：只要对应的二个二进位有一个为1时，结果位就为1。
+
+![或运算](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/或运算.6orep3gsrxc0.png)
+
+这个公式的作用就是将我们移位后的 res 的最后一位 0 变为 1。这个 1 也就代表着我们只出现一次元素的某一位。

gif-algorithm/求次数问题/只出现一次的数3.md

@@ -0,0 +1,107 @@
+## 只出现一次的数Ⅲ
+
+> 给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。
+
+示例 :
+
+> 输入: [1,2,1,3,2,5]
+> 输出: [3,5]
+
+这个也很容易理解，算是对第一题的升级，第一题有 1 个出现 1次的数，其余出现两次，这个题目中有 2 个出现 1次的数，其余数字出现两次。那么这个题目我们怎么做呢？我们看一下能不能利用第一题中的做法解决。
+
+### HashSet
+
+#### 解析
+
+这个做法和我们第一题的做法一致，只要理解了第一题的做法，这个很容易就能写出来，有一点不同的是，第一题的 HashSet 里面最后保留了一个元素，该题保留两个元素。
+
+#### 题目代码
+
+```java
+class Solution {
+    public int[] singleNumber(int[] nums) {
+        HashSet<Integer> set = new HashSet<Integer>();
+        for (int x : nums) {
+            //存在的则移除
+            if (set.contains(x)) {
+                set.remove(x);
+                continue;
+            }
+            //不存在存入
+            set.add(x);
+        }
+        //存到数组里，然后返回
+        int[] arr = new int[2];
+        int i = 0;
+        for (int y : set) {
+           arr[i++] = y; 
+        }
+        return arr;
+    }
+}
+```
+
+### 位运算
+
+#### 解析
+
+第一题中，我们可以通过异或运算直接求出目标数，但是我们第二题中不能直接用异或，是因为其他数字都出现三次，目标数出现一次。在这个题目中其他数字出现两次，目标数出现一次，但是这次的目标数为两个，我们直接异或运算的话，得到的数则为两个目标数的异或值，那么我们应该怎么做呢？
+
+我们试想一下，如果我们先将元素分成两组，然后每组包含一个目标值，那么异或之后，每组得到一个目标值，那么我们不就将两个目标值求出了吗？
+
+> 例： **a,b,a,b,c,d,e,f,e,f **      分组后
+>
+> A组：a, a , b, b, c     异或得到 c
+>
+> B组：e, e,  f,  f,  d     异或得到 d
+
+原理懂了，那么我们应该依据什么规则对其进行分类呢？
+
+c , d  两个不同的数，那么二进制上必定有一位是不同的，那么我们就可以根据这一位(分组位)来将 c , d 分到两个组中，数组中的其他元素，要么在 A 组中，要么在 B 组中。
+
+我们应该怎么得到分组位呢？
+
+我们让 c , d 异或即可，异或运算就是对应位不同时得 1 ,异或之后值为 1 的其中一位则为我们分组。
+
+例 001 ⊕  100 = 101，我们可以用最右边的 1 或最左边的 1 做为分组位，数组元素中，若我们将最右边的 1 作为我们的分组位，最后一位为 0 的则进入 A 组，为 1 的进入 B 组。
+
+那么我们应该怎么借助分组位进行分组呢？
+
+我们处理 c , d 的异或值，可以仅保留异或值的分组位，其余位变为 0 ，例如 101 变成 001或 100 
+
+为什么要这么做呢？在第二题提到，我们可以根据 a & 1 来判断 a 的最后一位为 0 还是为 1，所以我们将 101 变成 001 之后，然后数组内的元素  x & 001  即可对 x 进行分组 。同样也可以 x & 100 进行分组.
+
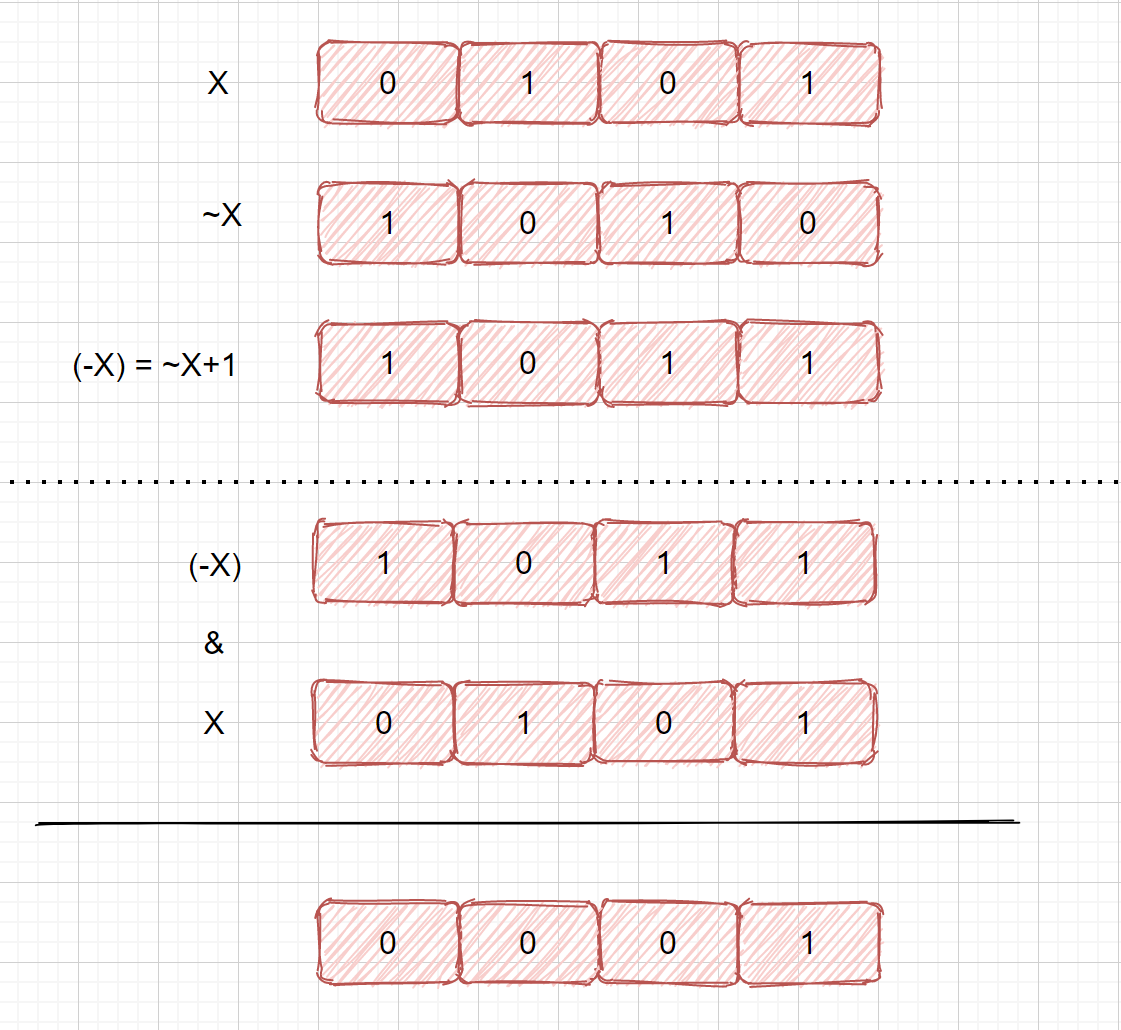
+那么我们如何才能仅保留分组位，其余位变为 0 呢？例 101 变为 001
+
+我们可以利用 x & (-x) 来保留最右边的 1  
+
+![分组位](https://cdn.jsdelivr.net/gh/tan45du/tan45du.github.io.photo@master/photo/分组位.25gbi25kv7c0.png)
+
+#### 题目代码：
+
+```java
+class Solution {
+    public int[] singleNumber(int[] nums) {
+        int temp = 0;
+        //求出异或值
+        for (int x : nums) {
+            temp ^= x;
+        }
+        //保留最右边的一个 1
+        int group = temp & (-temp);
+        System.out.println(group);
+        int[] arr = new int[2];
+        for (int y : nums) { 
+            //分组位为0的组，组内异或
+            if ((group & y) == 0) {
+                arr[0] ^= y;
+            //分组位为 1 的组，组内异或   
+            } else {
+                arr[1] ^= y;
+            }
+        }
+        return arr;
+    }
+}
+```
+