5.7 KiB
Morris
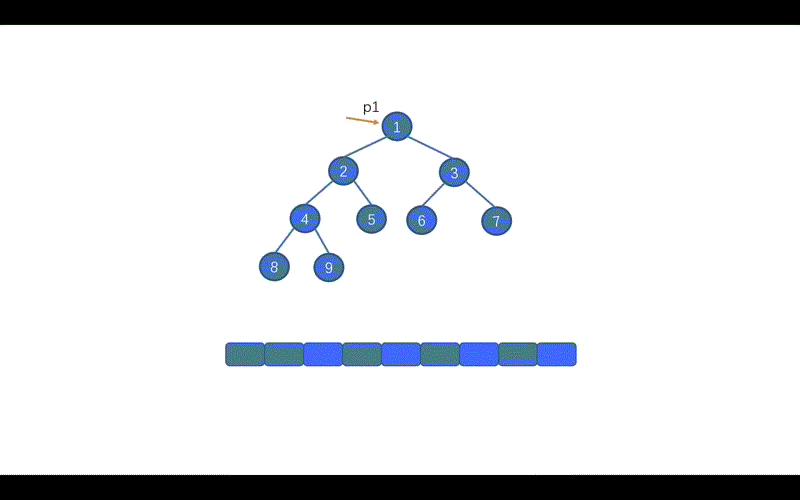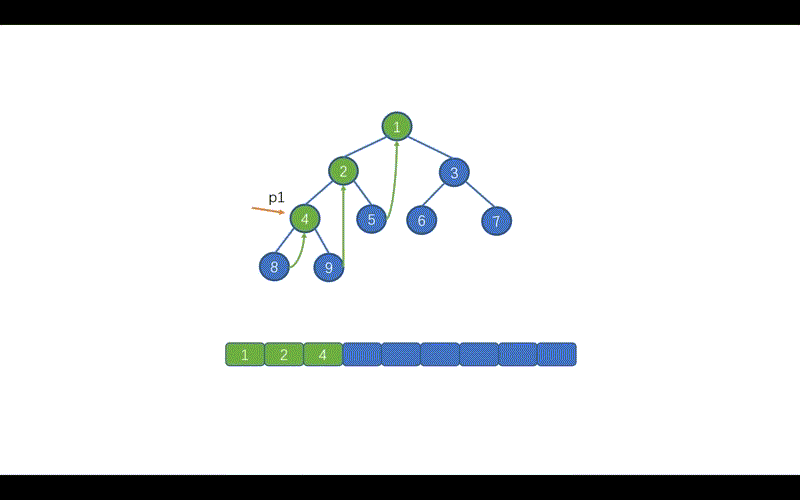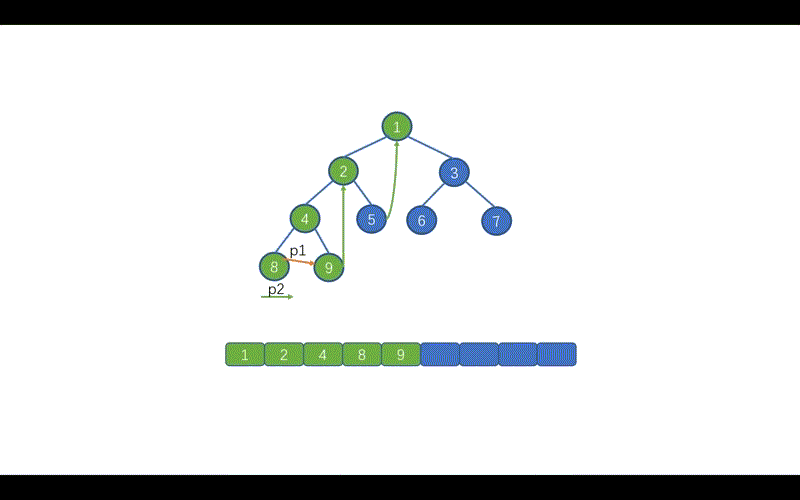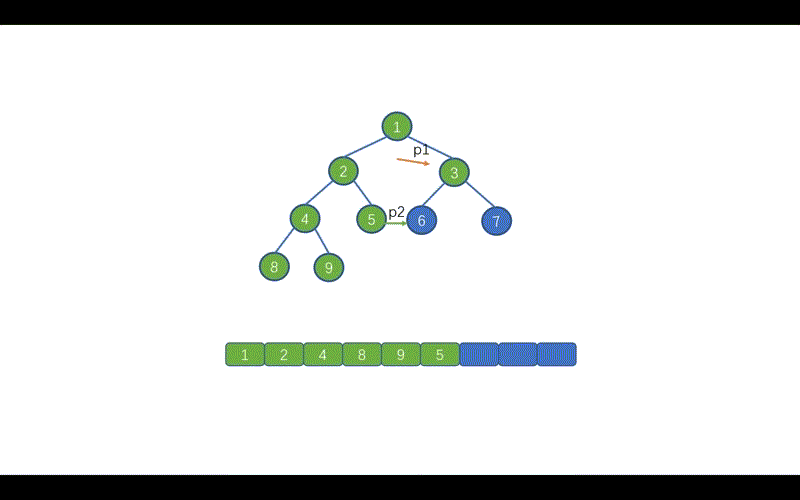
Morris 遍历利用树的左右孩子为空(大量空闲指针),实现空间开销的极限缩减。这个遍历方法,稍微有那么一丢丢难理解,不过结合动图,也就一目了然啦,下面我们先看动画吧。
看完视频,是不是感觉自己搞懂了,又感觉自己没搞懂,哈哈,咱们继续往下看。
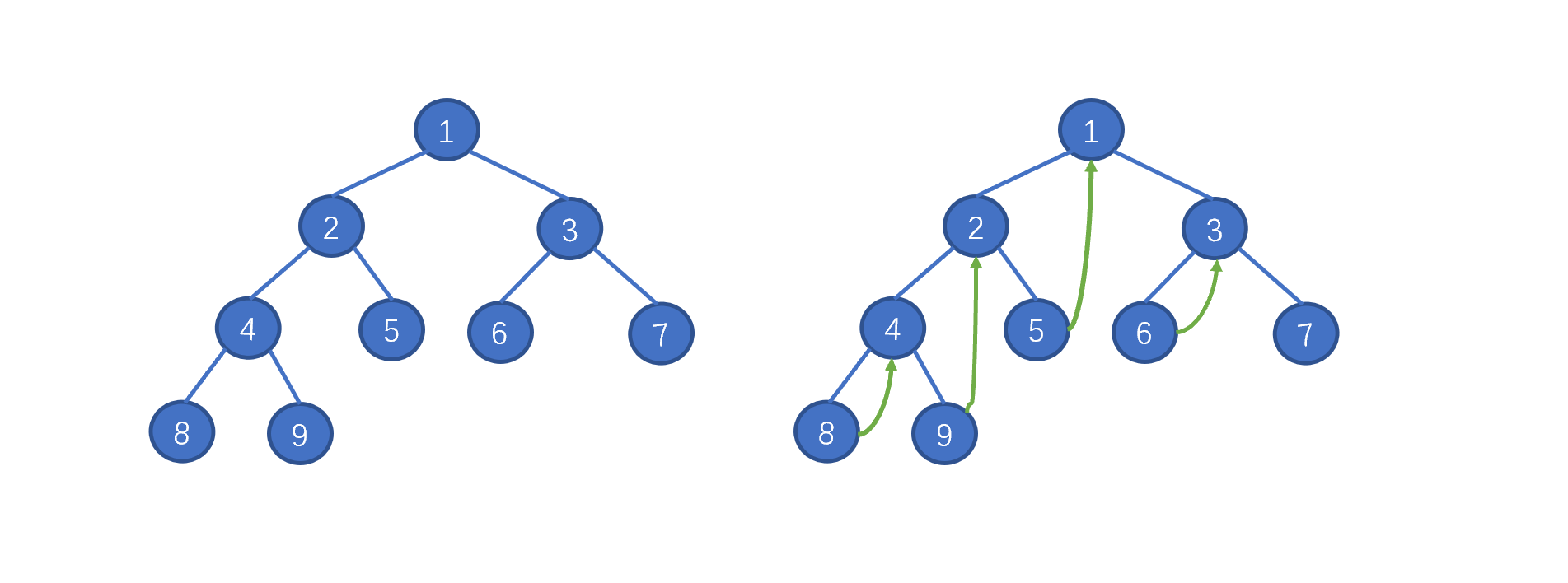
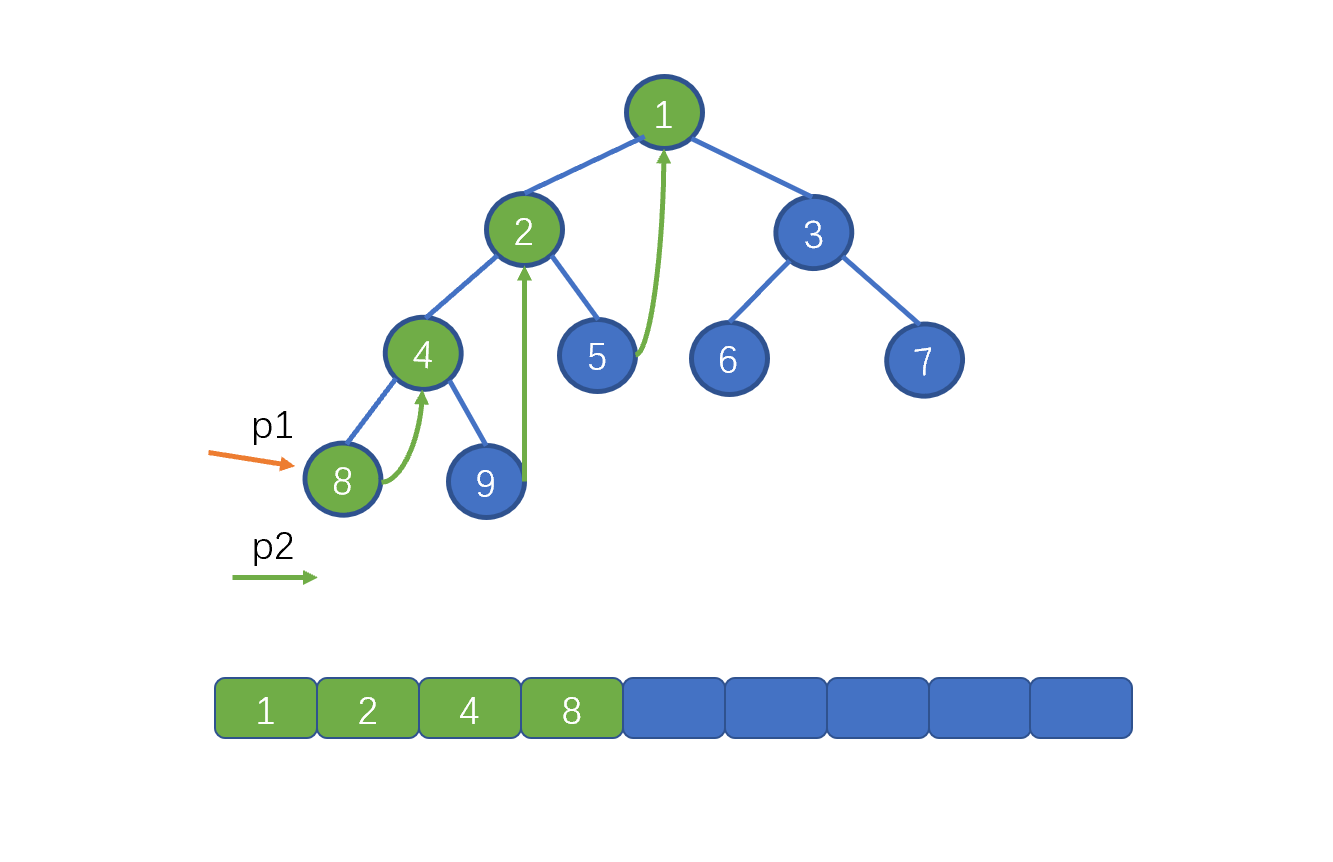
我们之前说的,Morris 遍历利用了树中大量空闲指针的特性,我们需要找到当前节点的左子树中的最右边的叶子节点,将该叶子节点的 right 指向当前节点。例如当前节点为 2,其左子树中的最右节点为 9 ,则在 9 节点添加一个 right 指针指向 2。
其实上图中的 Morris 遍历遵循两个原则,我们在动画中也能够得出。
-
当 p1.left == null 时,p1 = p1.right。(这也就是我们为什么要给叶子节点添加 right 指针的原因)
-
如果 p1.left != null,找到 p1 左子树上最右的节点。(也就是我们的 p2 最后停留的位置),此时我们又可以分为两种情况,一种是叶子节点添加 right 指针的情况,一种是去除叶子节点 right 指针的情况。
-
- 如果 p2 的 right 指针指向空,让其指向 p1,p1 向左移动,即 p1 = p1.left
- 如果 p2 的 right 指针指向 p1,让其指向空,(为了防止重复执行,则需要去掉 right 指针)p1 向右移动,p1 = p1.right。
这时你可以结合咱们刚才提到的两个原则,再去看一遍动画,并代入规则进行模拟,差不多就能完全搞懂啦。
下面我们来对动画中的内容进行拆解 ,
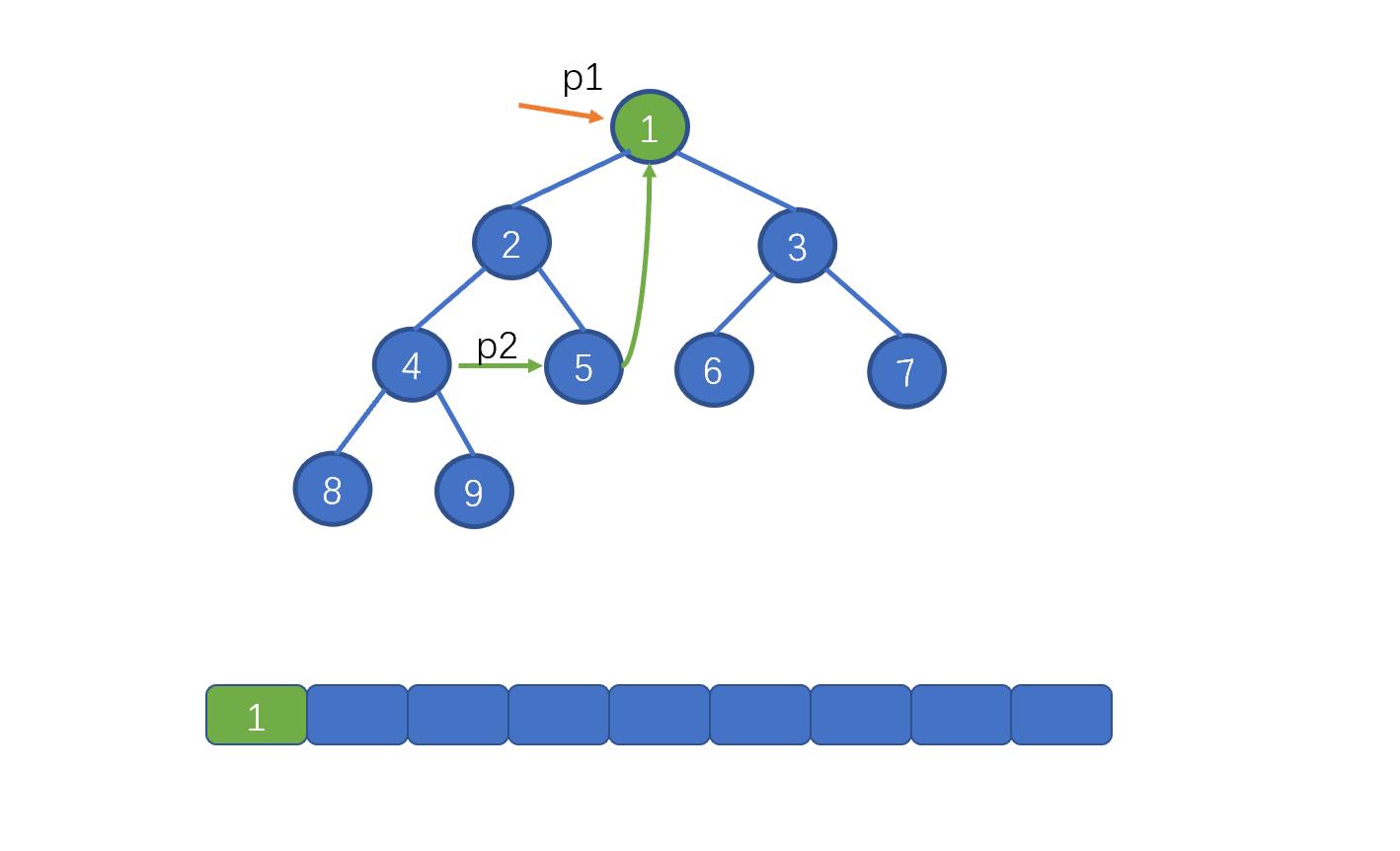
首先 p1 指向 root 节点
p2 = p1.left,下面我们需要通过 p2 找到 p1 的左子树中的最右节点。即节点 5,然后将该节点的 right 指针指向 root。并记录 root 节点的值。
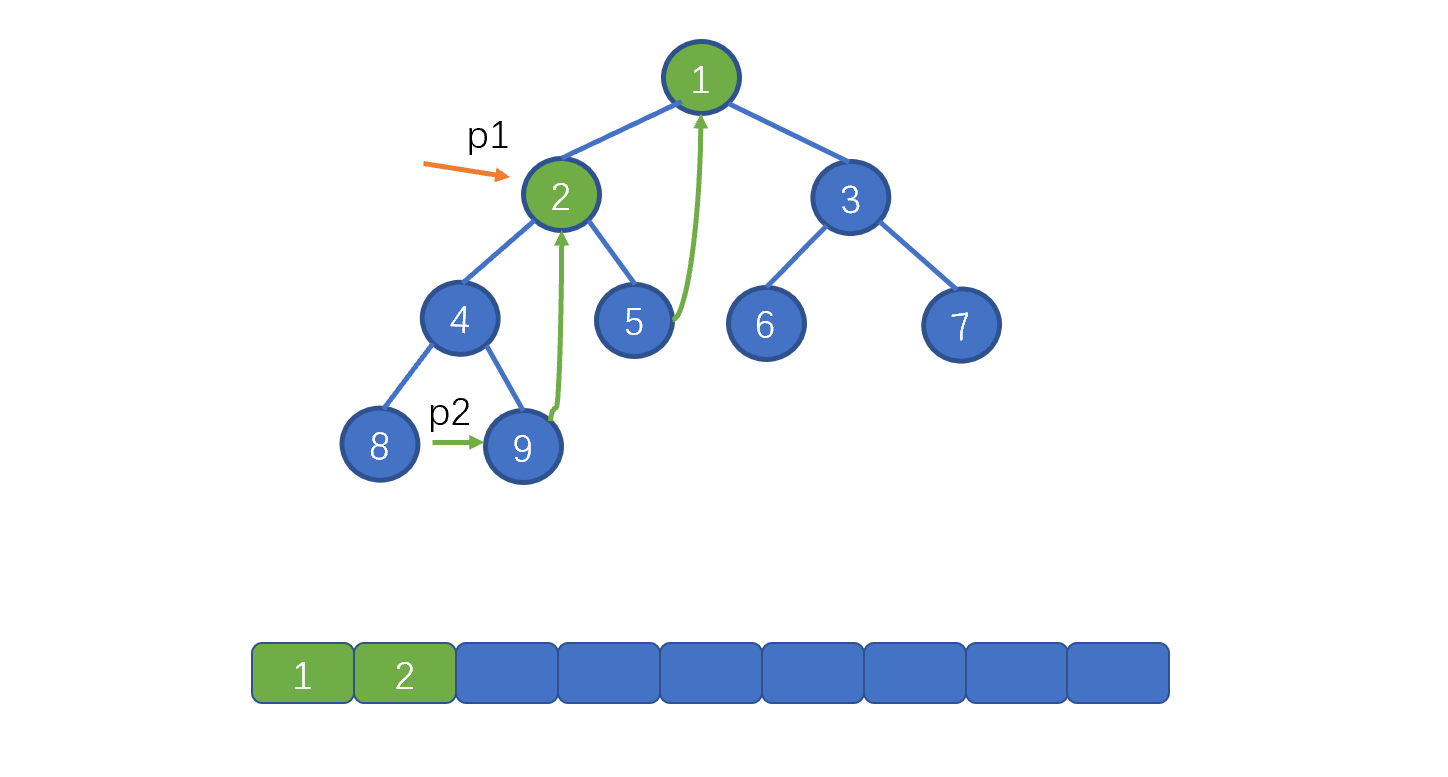
向左移动 p1,即 p1 = p1.left
p2 = p1.left ,即节点 4 ,找到 p1 的左子树中的最右叶子节点,也就是 9,并将该节点的 right 指针指向 2。
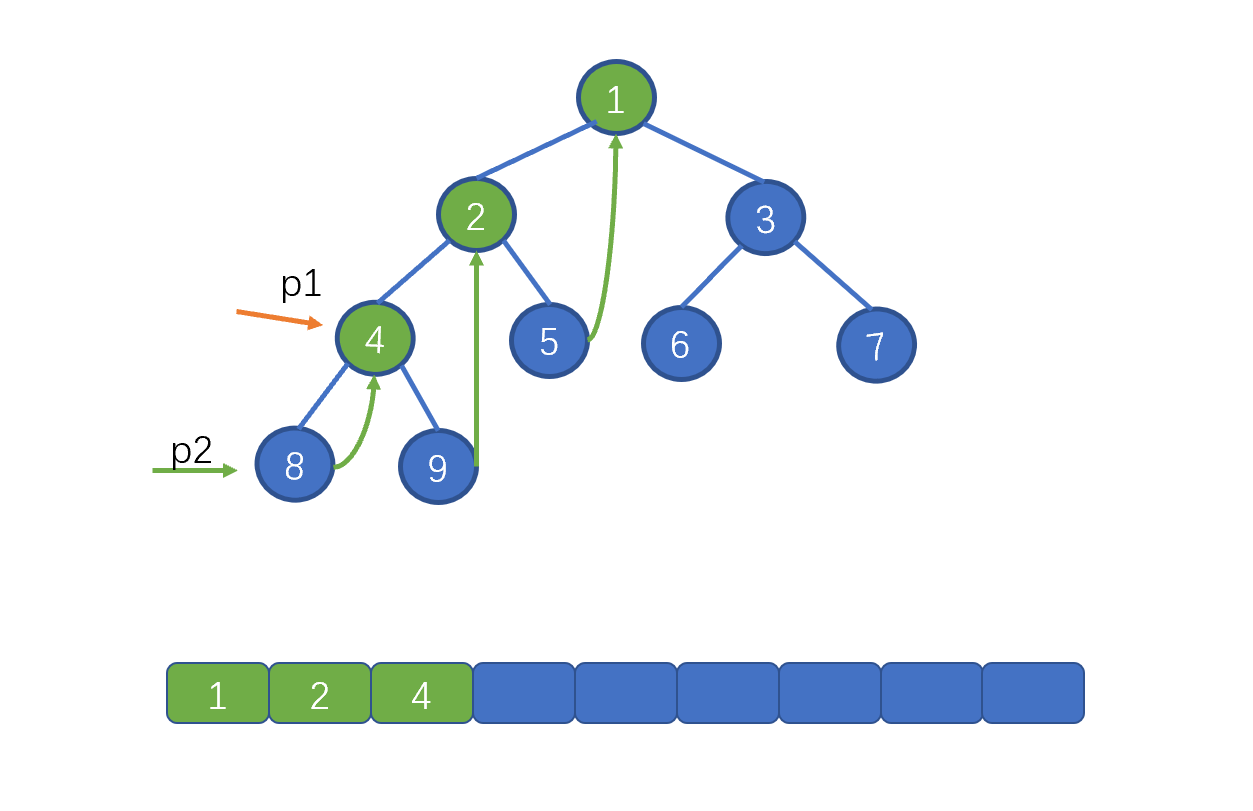
继续向左移动 p1,即 p1 = p1.left,p2 = p1.left。 也就是节点 8。并将该节点的 right 指针指向 p1。
我们发现这一步给前两步是一样的,都是找到叶子节点,将其 right 指针指向 p1,此时我们完成了添加 right 指针的过程,下面我们继续往下看。
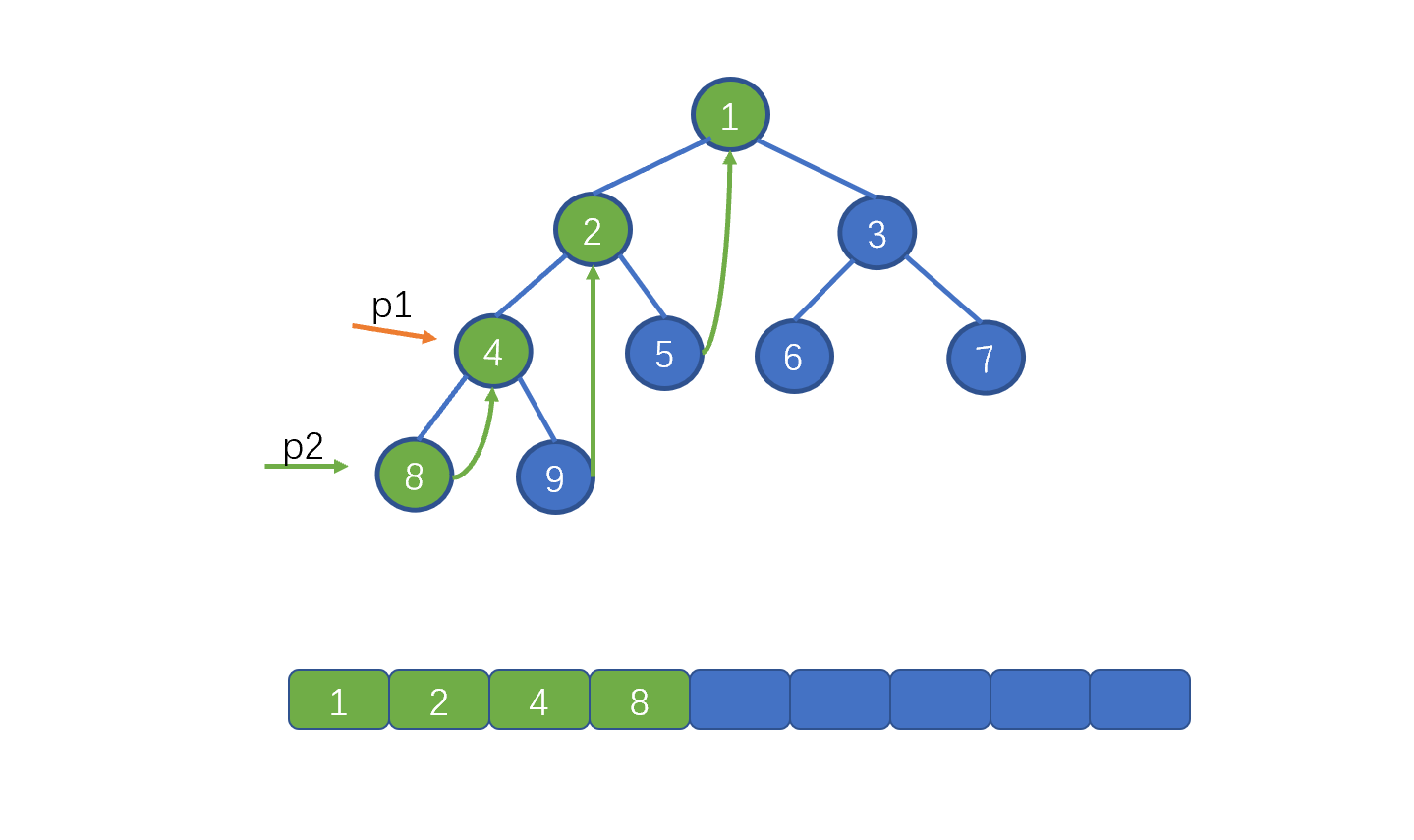
我们继续移动 p1 指针,p1 = p1.left。p2 = p.left。此时我们发现 p2 == null,即下图
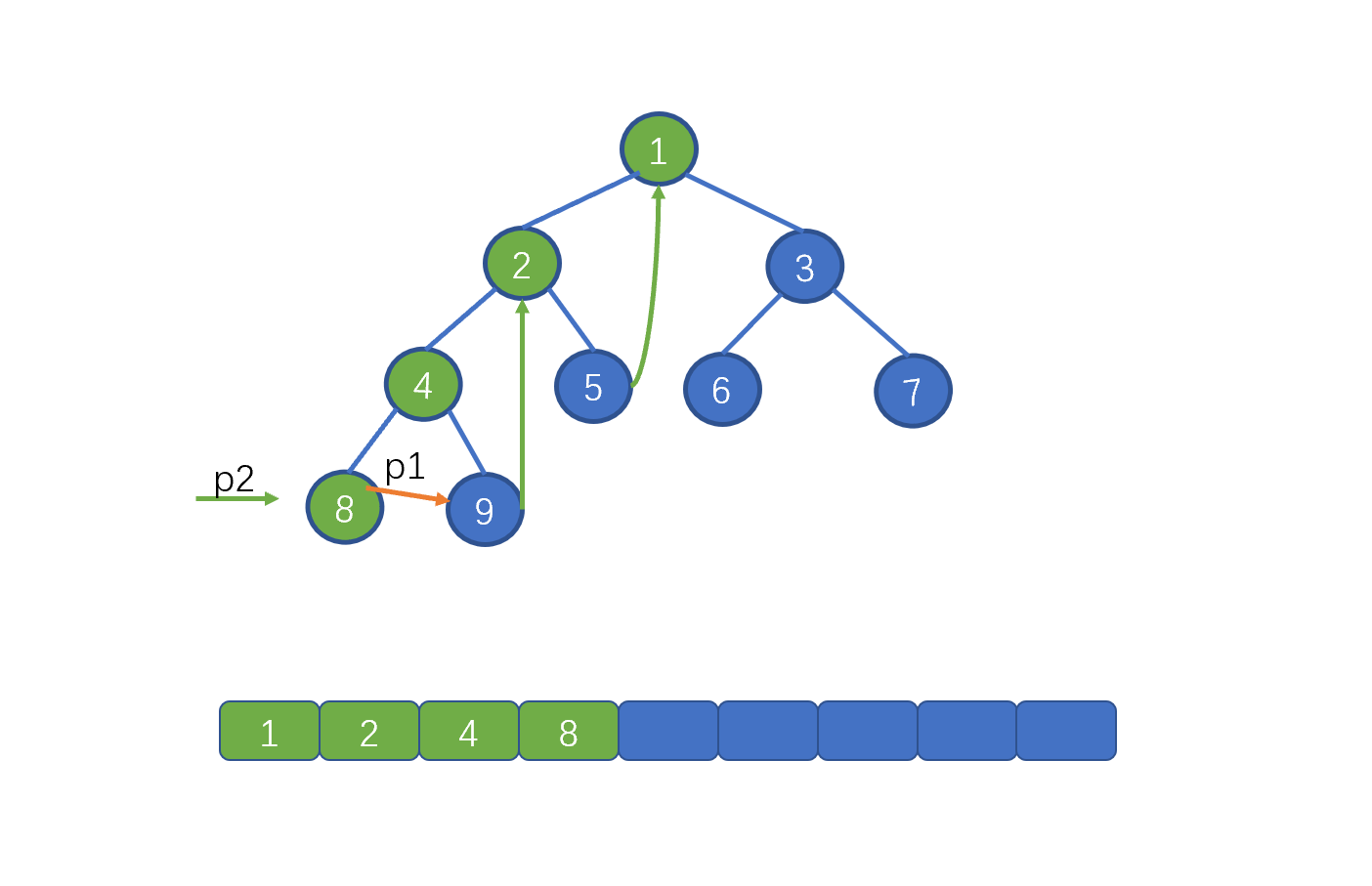
此时我们需要移动 p1, 但是不再是 p1 = p1.left 而是 p1 = p1.right。也就是 4,继续让 p2 = p1.left。此时则为下图这种情况
此时我们发现 p2.right != null 而是指向 4,说明此时我们已经添加过了 right 指针,所以去掉 right 指针,并让 p1 = p1.right
下面则继续移动 p1 ,按照规则继续移动即可,遇到的情况已经在上面做出了举例,所以下面我们就不继续赘述啦,如果还不是特别理解的同学,可以再去看一遍动画加深下印象。
时间复杂度 O(n),空间复杂度 O(1)
下面我们来看代码吧。
代码
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) {
return list;
}
TreeNode p1 = root; TreeNode p2 = null;
while (p1 != null) {
p2 = p1.left;
if (p2 != null) {
//找到左子树的最右叶子节点
while (p2.right != null && p2.right != p1) {
p2 = p2.right;
}
//添加 right 指针,对应 right 指针为 null 的情况
if (p2.right == null) {
list.add(p1.val);
p2.right = p1;
p1 = p1.left;
continue;
}
//对应 right 指针存在的情况,则去掉 right 指针
p2.right = null;
} else {
list.add(p1.val);
}
//移动 p1
p1 = p1.right;
}
return list;
}
}
Swift Code:
class Solution {
func preorderTraversal(_ root: TreeNode?) -> [Int] {
var list:[Int] = []
guard root != nil else {
return list
}
var p1 = root, p2: TreeNode?
while p1 != nil {
p2 = p1!.left
if p2 != nil {
//找到左子树的最右叶子节点
while p2!.right != nil && p2!.right !== p1 {
p2 = p2!.right
}
//添加 right 指针,对应 right 指针为 null 的情况
if p2!.right == nil {
list.append(p1!.val)
p2!.right = p1
p1 = p1!.left
continue
}
//对应 right 指针存在的情况,则去掉 right 指针
p2!.right = nil
} else {
list.append(p1!.val)
}
//移动 p1
p1 = p1!.right
}
return list
}
}
好啦,今天就看到这里吧,咱们下期见!