mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-01 17:53:39 +00:00
3.9 KiB
3.9 KiB
41. 缺失的第一个正数
给你一个未排序的整数数组,请你找出其中没有出现的最小的正整数。
示例 1:
输入: [1,2,0] 输出: 3
示例 2:
输入: [3,4,-1,1] 输出: 2
示例 3:
输入: [7,8,9,11,12] 输出: 1
重复遍历
让我们找出缺失的最小正整数,而且这是一个未排序的数组,我们可以利用暴力求解,挨个遍历发现那个不存在直接返回即可。我们这里使用两种方法解决这个问题,大家也可以提出自己的做法。
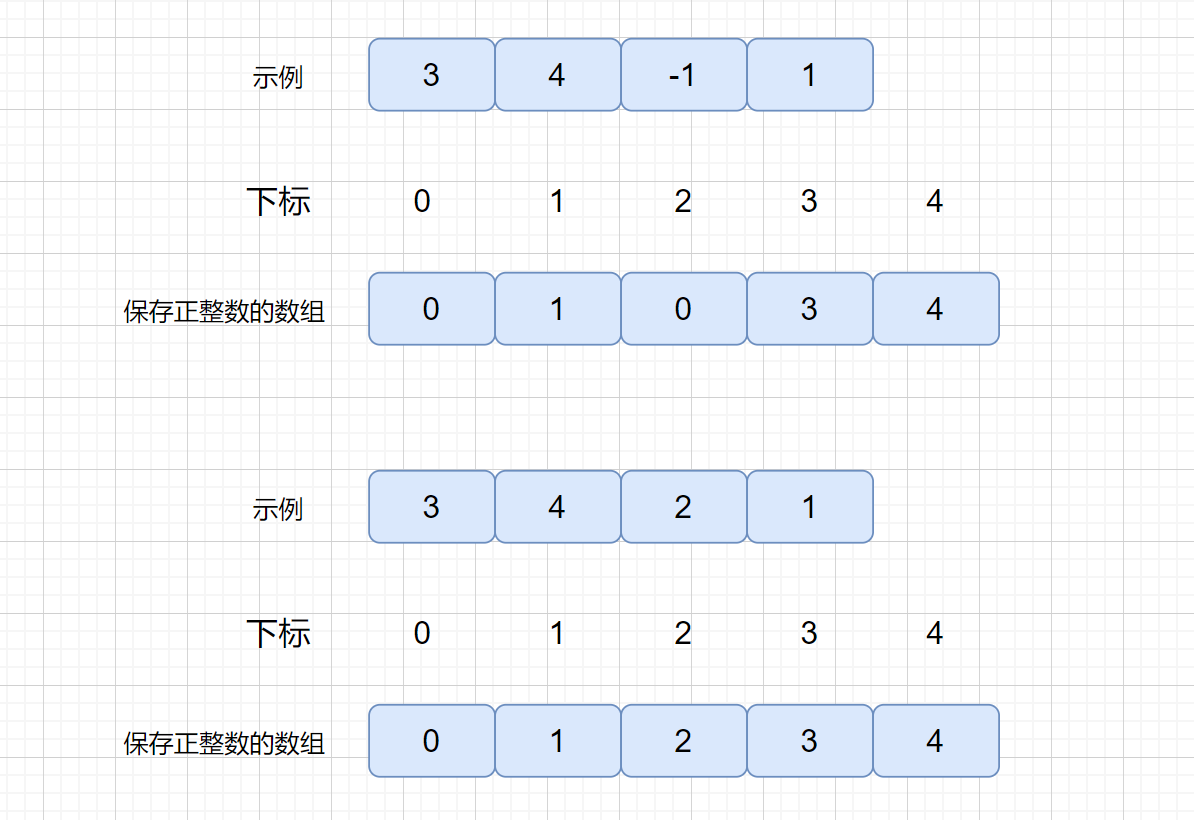
我们既然是返回缺失的正整数,那么我们则可以将这个数组中的所有正整数保存到相应的位置,见下图。
上图中,我们遍历一遍原数组,将正整数保存到新数组中,然后遍历新数组,第一次发现 newnum[i] != i 时,则说明该值是缺失的,返回即可,例如我上图中的第一个示例中的 2,如果遍历完新数组,发现说所有值都对应,说明缺失的是 新数组的长度对应的那个数,比如第二个示例中 ,新数组的长度为 5,此时缺失的为 5,返回长度即可,很容易理解。
注:我们发现我们新的数组长度比原数组大 1,是因为我们遍历新数组从 1,开始遍历。
动图解析
class Solution {
public int firstMissingPositive(int[] nums) {
if (nums.length == 0) {
return 1;
}
//因为是返回第一个正整数,不包括 0,所以需要长度加1,细节1
int[] res = new int[nums.length + 1];
//将数组元素添加到辅助数组中
for (int x : nums) {
if (x > 0 && x < res.length) {
res[x] = x;
}
}
//遍历查找,发现不一样时直接返回
for (int i = 1; i < res.length; i++) {
if (res[i] != i) {
return i;
}
}
//缺少最后一个,例如 1,2,3此时缺少 4 ,细节2
return res.length;
}
}
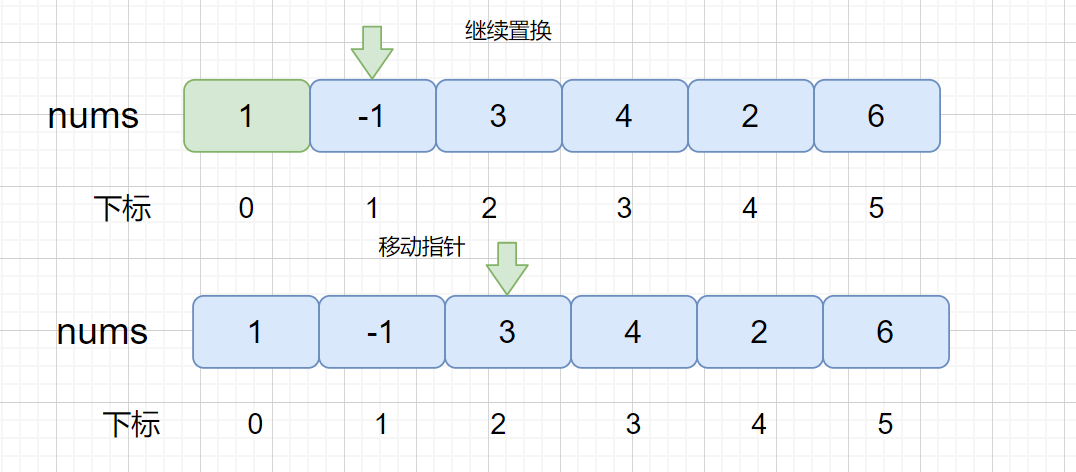
我们通过上面的例子了解这个解题思想,我们有没有办法不使用辅助数组完成呢?我们可以使用原地置换,直接在 nums 数组内,将值换到对应的索引处,与上个方法思路一致,只不过没有使用辅助数组,理解起来也稍微难理解一些。
下面我们看一下原地置换的一些情况。
注:红色代表待置换,绿色代表置换完毕
动图解析:
题目代码:
class Solution {
public int firstMissingPositive(int[] nums) {
int len = nums.length;
if (len == 0) {
return 1;
}
for (int i = 0; i < len; ++i) {
//需要考虑指针移动情况,大于0,小于len+1,不等与i+1,两个交换的数相等时,防止死循环
while (nums[i] > 0 && nums[i] < len + 1 && nums[i] != i+1 && nums[i] != nums[nums[i]-1]) {
swap(nums,i,nums[i] - 1);
}
}
//遍历寻找缺失的正整数
for (int i = 0; i < len; ++i) {
if(nums[i] != i+1) {
return i+1;
}
}
return len + 1;
}
//交换
public void swap(int[] nums, int i, int j) {
if (i != j) {
nums[i] ^= nums[j];
nums[j] ^= nums[i];
nums[i] ^= nums[j];
}
}
}