4.4 KiB
只出现一次的数Ⅱ
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
示例 1:
输入: [2,2,3,2] 输出: 3
示例 2:
输入: [0,1,0,1,0,1,99] 输出: 99
题目很容易理解,刚才的题目是其他元素出现两次,目标元素出现一次,该题是其他元素出现三次,目标元素出现一次,所以我们完全可以借助上题的一些做法解决该题。
求和法
解析
我们在上题中介绍了求和法的解题步骤,现在该题中其他元素都出现三次,我们的目标元素出现一次,所以我们利用求和法也是完全 OK 的。下面我们来看具体步骤吧。
1.通过遍历数组获取所有元素的和以及 HashSet 内元素的和。
2.(SumSet * 3 - SumNum)/ 2即可,除以 2 是因为我们减去之后得到的是 2 倍的目标元素。
注:这个题目中需要注意溢出的情况 。
题目代码
class Solution {
public int singleNumber(int[] nums) {
HashSet<Integer> set = new HashSet<>();
long sumset = 0;
long sumnum = 0;
for (int x : nums) {
//所有元素的和
sumnum += x;
if (set.contains(x)) {
continue;
}
//HashSet元素和
sumset += x;
set.add(x);
}
//返回只出现一次的数
return (int)((3 * sumset - sumnum) / 2);
}
}
这个题目用 HashMap 和排序查找肯定也是可以的,大家可以自己写一下,另外我们在第一题中有个利用异或求解的方法,但是这个题目是出现三次,我们则不能利用直接异或来求解,那还有其他方法吗?
位运算
解析
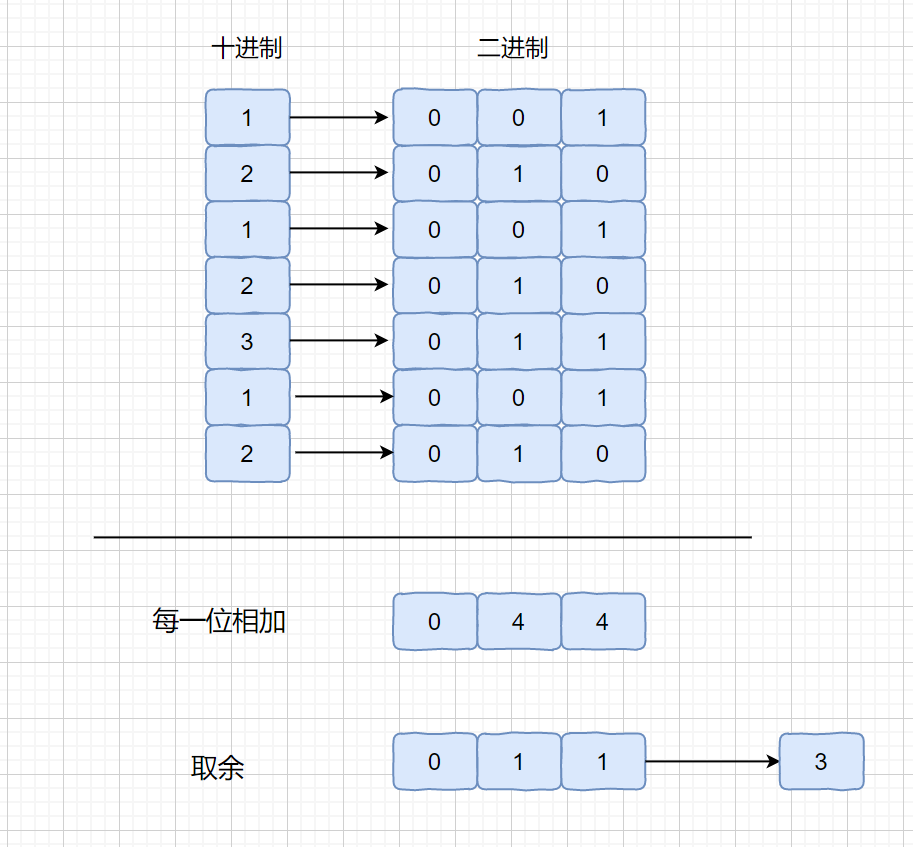
这个方法主要做法是将我们的数的二进制位每一位相加,然后对其每一位的和取余 ,我们看下面的例子。
那么我们为什么要这样做呢?大家想一下,如果其他数都出现 3 次,只有目标数出现 1 次,那么每一位的 1 的个数无非有这2种情况,为 3 的倍数(全为出现三次的数) 或 3 的倍数 +1(包含出现一次的数)。这个 3 的倍数 +1 的情况也就是我们的目标数的那一位。
题目代码
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for(int i = 0; i < 32; i++){
int count = 0;
for (int j = 0; j < nums.length; j++) {
//先将数右移,并求出最后一位为 1 的个数
if ((nums[j] >> i & 1) == 1) {
count++;
}
}
//找到某一位取余为 1 的数,并左移,为了将这一位循环结束后移至原位
if (count % 3 != 0) {
res = res | 1 << i;
}
}
return res;
}
}
我们来解析一下我们的代码
<< 左移动运算符:运算数的各二进位全部左移若干位,由 << 右边的数字指定了移动的位数,高位丢弃,低位补0。
>> 右移动运算符:把">>"左边的运算数的各二进位全部右移若干位,>> 右边的数字指定了移动的位数
另外我们的代码中还包含了 a & 1 和 a | 1 这有什么作用呢?继续看下图
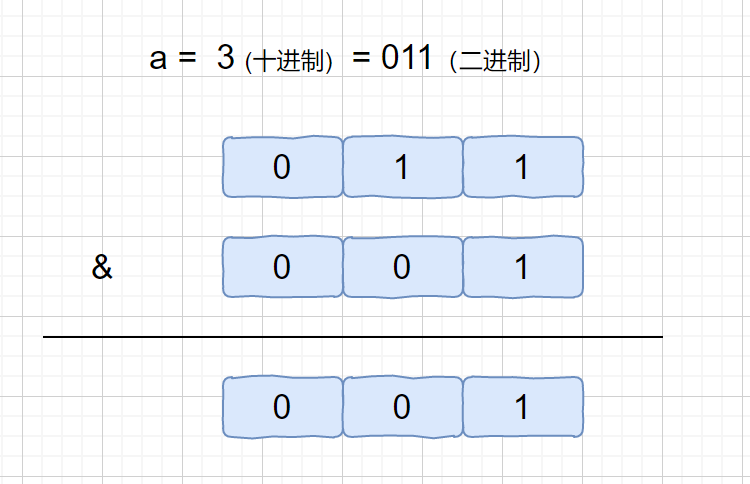
& 按位与运算符:参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0
因为我们 a & 1 中 1 只有最后一位为 1,其余位皆为 0 ,所以我们发现 a & 1的作用就是判断 a 的最后一位是否为 1 ,如果 a 的最后一位为 1 ,a & 1 = 1,否则为 0 。所以我们还可以通过这个公式来判断 a 的奇偶性。
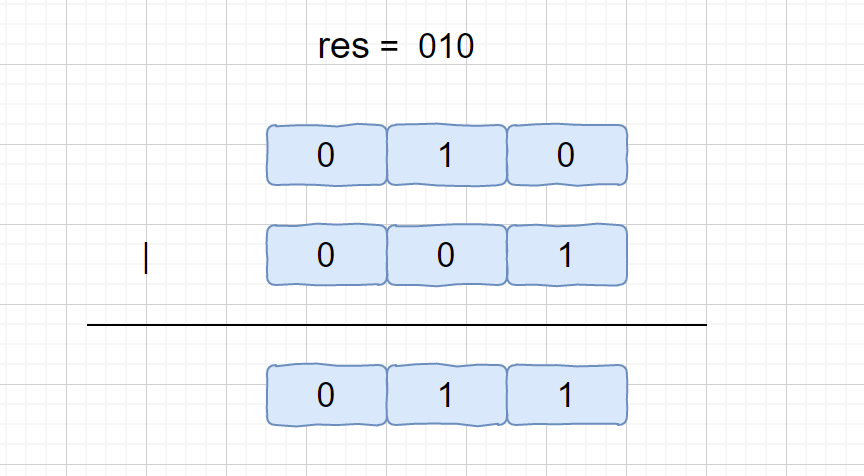
| 按位或运算符:只要对应的二个二进位有一个为1时,结果位就为1。
这个公式的作用就是将我们移位后的 res 的最后一位 0 变为 1。这个 1 也就代表着我们只出现一次元素的某一位。