5.3 KiB
链表详解
如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 tan45du_one ,备注 github + 题目 + 问题 向我反馈
感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
另外希望手机阅读的同学可以来我的 公众号:程序厨 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击刷题小队进入。
阅读完本文你会有以下收获
1.知道什么是链表?
2.了解链表的几种类型。
3.了解链表如何构造。
4.链表的存储方式
5.如何遍历链表
6.了解链表的操作。
7.知道链表和数组的不同点
8.掌握链表的经典题目。
链表的定义:
定义:链表是一种递归的数据结构,他或者为空(null),或者是指向一个结点(node)的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。
我们来对其解读一下,链表是一种常见且基础的数据结构,是一种线性表,但是他不是按线性顺序存取数据,而是在每一个节点里存到下一个节点的地址。我们可以这样理解,链表是通过指针串联在一起的线性结构,每一个链表结点由两部分组成,数据域及指针域,链表的最后一个结点指向 null。也就是我们所说的空指针。
链表的几种类型
我们先来看一下链表的可视化表示方法,以便更好的对其理解。
- 用长方形表示对象
- 将实例变量的值写在长方形中;
- 用指向被引用对象的箭头表示引用关系。
单链表
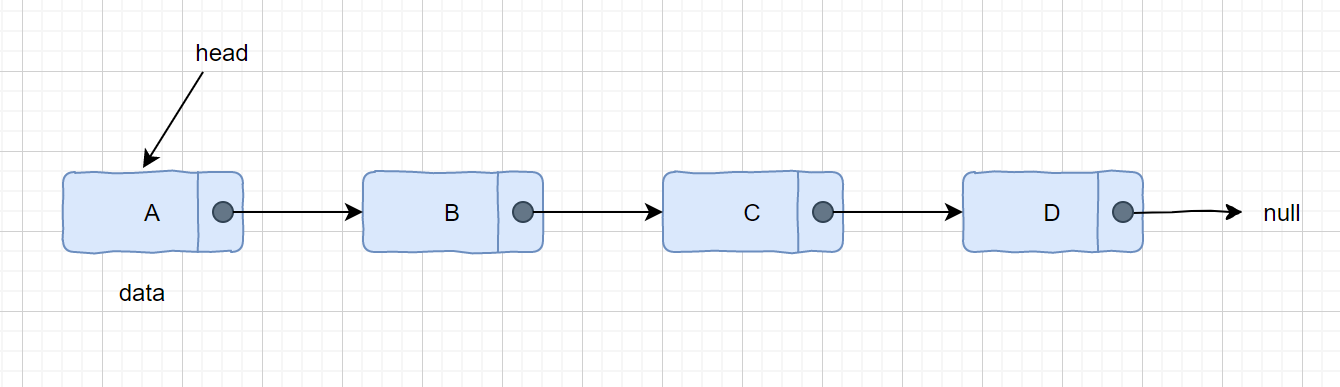
一个单向链表包含两个值: 当前节点的值和一个指向下一个节点的链接。
我们通过上面说到的可视化表示方法,构造单链表的可视化模型,如图所示。
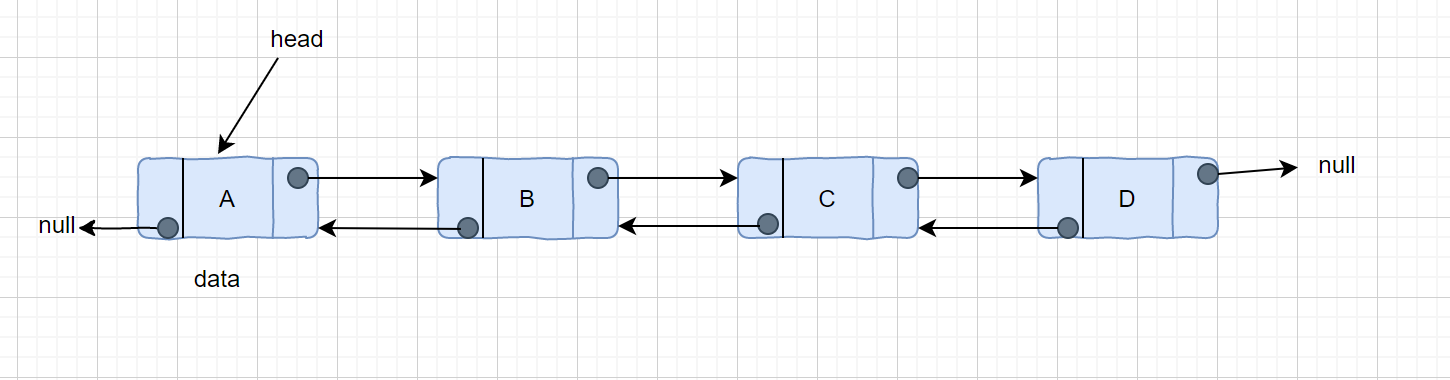
双向链表
上面提到了单链表的节点只能指向节点的下一个节点。而双向链表有三个整数值: 数值、向后的节点链接、向前的节点链接,所以双链表既能向前查询也可以向后查询。
还有一个常用的链表则为循环单链表,则单链表尾部的指针指向头节点。例如在 leetcode61 旋转链表中,我们就是先将链表闭合成环,找到新的打开位置,并定义新的表头和表尾。
构造链表
java 是面向对象语言,实现链表很容易。我们首先用一个嵌套类来定义节点的抽象数据类型
private class Node {
Item item;
Node next;
}
现在我们需要构造一条含有 one,two,three 的链表,我们首先为每个元素创造一个节点
Node first = new Node();
Node second = new Node();
Node third = new Node();
将每个节点的 item 域设为所需的值
first.item = "one";
second.item = "two";
third.item = "three";
然后我们设置 next 域来构造链表
first.next = second;
second.next = third;
注:此时 third 的 next 仍为 null,即被初始化的值。
链表的存储方式
我们知道了如何构造链表,我们再来说一下链表的存储方式。
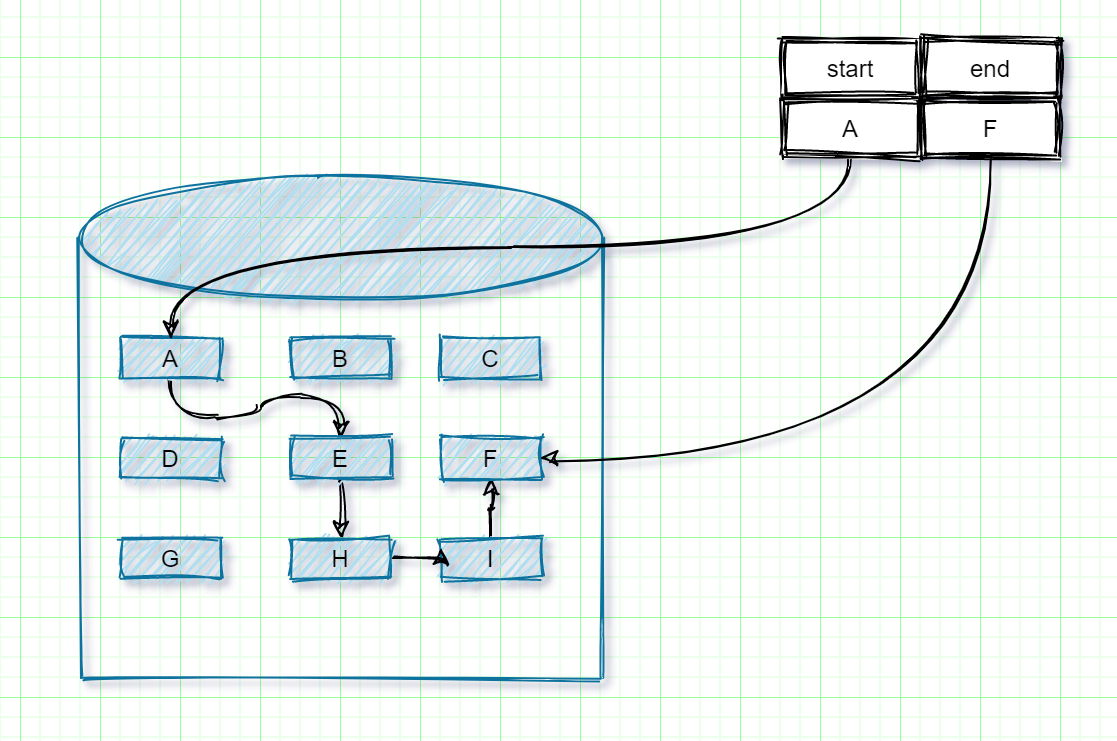
我们都知道数组在内存中是连续分布的,但是链表在内存不是连续分配的。链表是通过指针域的指针链接内存中的各个节点。
所以链表在内存中是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。我们可以根据下图来进行理解。
遍历链表
链表的遍历我们通常使用 while 循环(for 循环也可以但是代码不够简洁)下面我们来看一下链表的遍历代码
for:
for (Node x = first; x != null; x = x.next) {
//处理x.item
}
while:
Node x = first;
while (x!=null) {
//处理x.item
x = x.next;
}
链表的几种操作
添加节点
删除节点
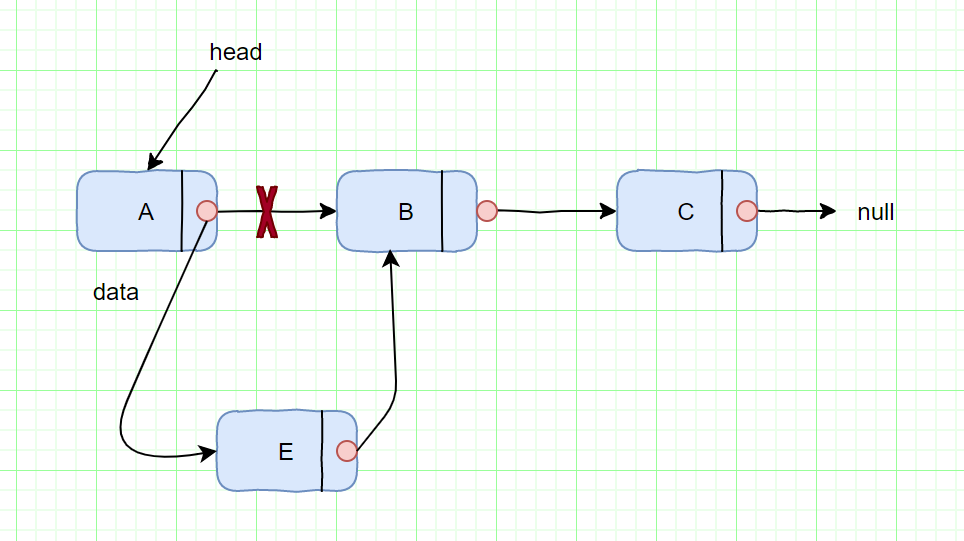
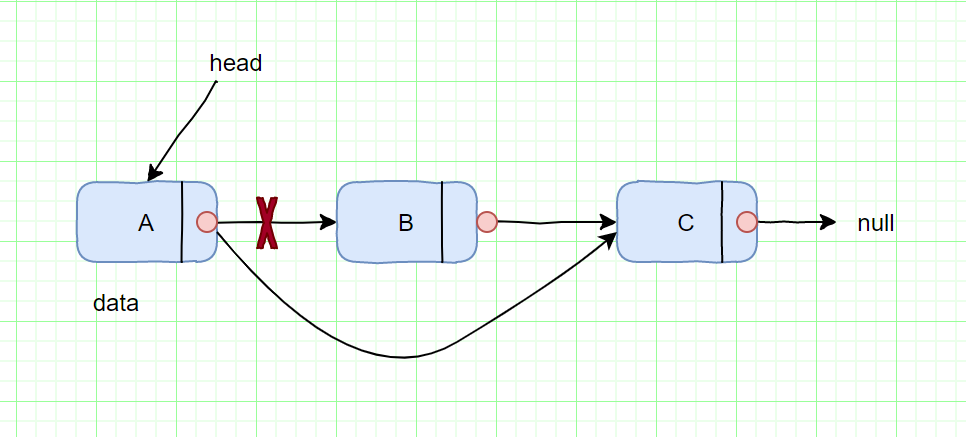
删除 B 节点,如图所示
我们只需将 A 节点的 next 指针指向 C 节点即可。
有的同学可能会有这种疑问,B 节点这样不会留着内存里吗?java 含有自己的内存回收机制,不用自己手动释放内存了,但是 C++,则需要手动释放。
我们通过上图的删除和插入都是 O(1)操作。
链表和数组的比较
| 插入/删除操作(时间复杂度) | 查询(时间复杂度) | 存储方式 | |
|---|---|---|---|
| 数组 | O(n) | O(1) | 内存连续分布 |
| 链表 | O(1) | O(n) | 内存散乱分布 |