4.5 KiB
如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 tan45du_one ,备注 github + 题目 + 问题 向我反馈
感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
另外希望手机阅读的同学可以来我的 公众号:程序厨 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击刷题小队进入。
简单选择排序
我们的冒泡排序不断进行交换,通过交换完成最终的排序,我们的简单选择排序的思想也很容易理解,主要思路就是我们每一趟在 n-i+1 个记录中选取关键字最小的记录作为有序序列的第 i 个记录。
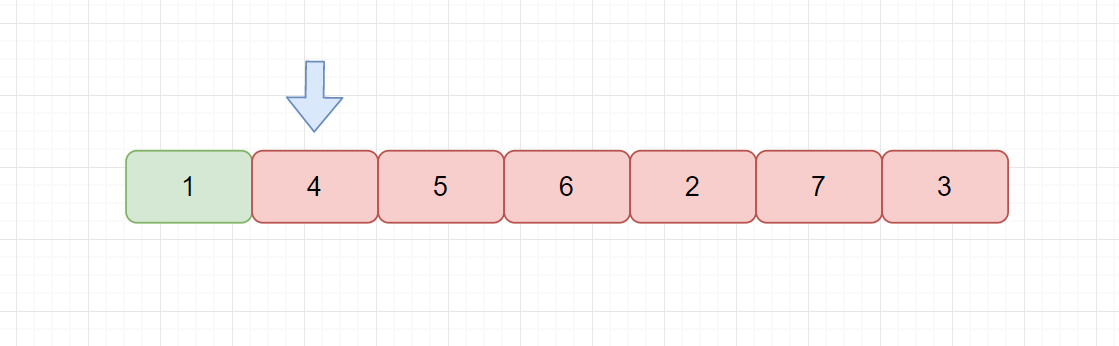
例如上图,绿色代表已经排序的元素,红色代表未排序的元素。我们当前指针指向 4 ,则我们遍历红色元素,从中找到最小值,然后与 4 交换。我们发现选择排序执行完一次循环也至少可以将 1 个元素归位。
下面我们来看一下代码的执行过程,看过之后肯定能写出代码的。
注:我们为了更容易理解,min 值保存的是值,而不是索引,实际代码中保存的是索引
简单选择排序代码
Java Code:
class Solution {
public int[] sortArray(int[] nums) {
int len = nums.length;
int min = 0;
for (int i = 0; i < len; ++i) {
min = i;
//遍历到最小值
for (int j = i + 1; j < len; ++j) {
if (nums[min] > nums[j]) min = j;
}
if (min != i) swap(nums,i,min);
}
return nums;
}
public void swap (int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
Python Code:
from typing import List
class Solution:
def sortArray(self, nums: List[int])->List[int]:
leng = len(nums)
min = 0
for i in range(0, leng):
min = i
# 遍历到最小值
for j in range(i + 1, leng):
if nums[min] > nums[j]:
min = j
if min != i:
self.swap(nums, i, min)
return nums
def swap(self, nums: List[int], i: int, j: int):
temp = nums[i]
nums[i] = nums[j]
nums[j] = temp
简单选择排序时间复杂度分析
从简单选择排序的过程来看,他最大的特点就是交换移动数据次数相当少,这样也就节省了排序时间,简单选择和冒泡排序不一样,我们发现无论最好情况和最坏情况,元素间的比较次数是一样的,第 i 次排序,需要 n - i 次比较,n 代表数组长度,则一共需要比较(n-1) + (n-2) +.... + 2 + 1= n*(n-1)/2 次,对于交换而言,最好情况交换 0 次,最坏情况(逆序时)交换 n - 1 次。那么简单选择排序时间复杂度也为 O(n^2) 但是其交换次数远小于冒泡排序,所以其效率是好于冒泡排序的。
简单选择排序空间复杂度分析
由我们动图可知,我们的简单选择排序只用到了常量级的额外空间,所以空间复杂度为 O(1)。
简单选择排序稳定性分析
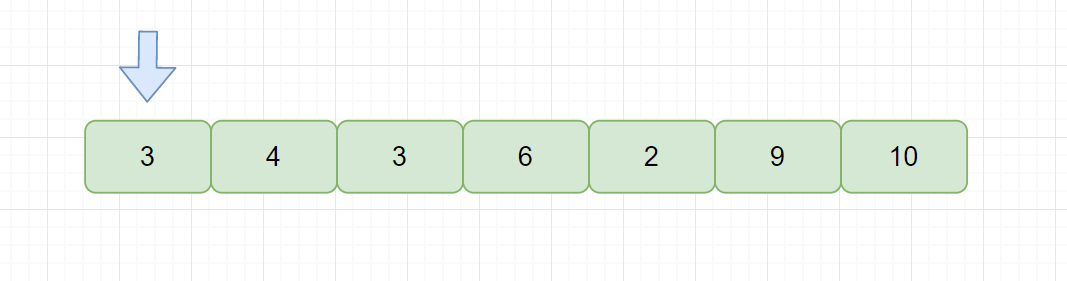
我们思考一下,我们的简单选择排序是稳定的吗?显然不是稳定的,因为我们需要在指针后面找到最小的值,与指针指向的值交换,见下图。
此时我们需要从后面元素中找到最小的元素与指针指向元素交换,也就是元素 2 。但是我们交换后发现,两个相等元素 3 的相对位置发生了改变,所以简单选择排序是不稳定的排序算法。
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|---|---|---|
| 简单选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |