mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-28 14:58:55 +00:00
207 lines
8.5 KiB
Java
207 lines
8.5 KiB
Java
# 我太喜欢这个题了
|
||
|
||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||
>
|
||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||
>
|
||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||
|
||
今天我们来看一道贼棒的题目,题目不长,很经典,也很容易理解,我们一起来看一哈吧,
|
||
|
||
大家也可能做过这道题,那就再复习一下,如果没做过的话,可以看完文章,自己去 AC 一下,不过写代码的时候,要自己完全写出来,这样才能有收获,下面我们看题目吧。
|
||
|
||
## leetcode 233. 数字 1 的个数
|
||
|
||
**题目描述**
|
||
|
||
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
|
||
|
||
示例 1:
|
||
|
||
> 输入:n = 13
|
||
> 输出:6
|
||
|
||
示例 2:
|
||
|
||
> 输入:n = 0
|
||
> 输出:0
|
||
|
||
太喜欢这种简洁的题目啦,言简意赅,就是让咱们找出**小于等于 n 的非负整数中数字 1 出现的个数**。
|
||
|
||
大家看到这个题目的第一印象,可能会这样想,哦,让我们求 1 的个数。
|
||
|
||
呐我们直接逐位遍历每个数的每一位,当遇到 1 的时候,计数器 +1,不就行了。
|
||
|
||
嗯,很棒的方法,可惜会超时。(我试了)
|
||
|
||
或者说,我们可以先将所有数字拼接起来,然后再逐位遍历,这样仍会超时。(我也试了)
|
||
|
||
大家再思考一下还有没有别的方法呢?
|
||
|
||
既然题目让我们统计小于等于 n 的非负整数中数字 1 出现的个数。
|
||
|
||
那我们可以不可这样统计。
|
||
|
||
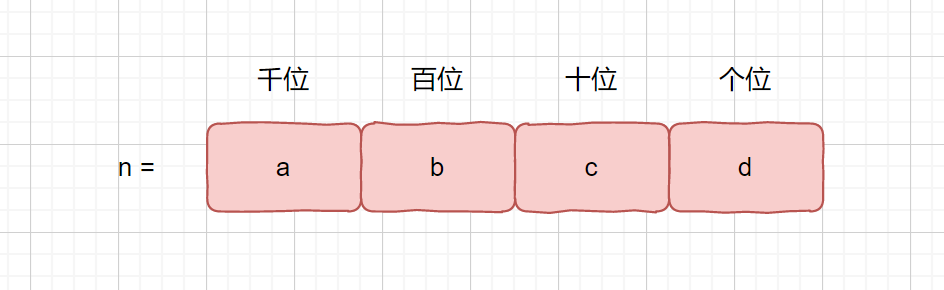
我们假设 n = abcd,某个四位数。
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
那我们完全可以统计每一位上 1 出现的次数,个数上 1 出现的次数,十位上 1 出现的次数,百位 ,千位。。。
|
||
|
||
也就是说**小于等于 n 的所有数字中**,个位上出现 1 的次数 + 十位出现 1 的次数 + 。。。最后得到的就是总的出现次数。
|
||
|
||
见下图
|
||
|
||
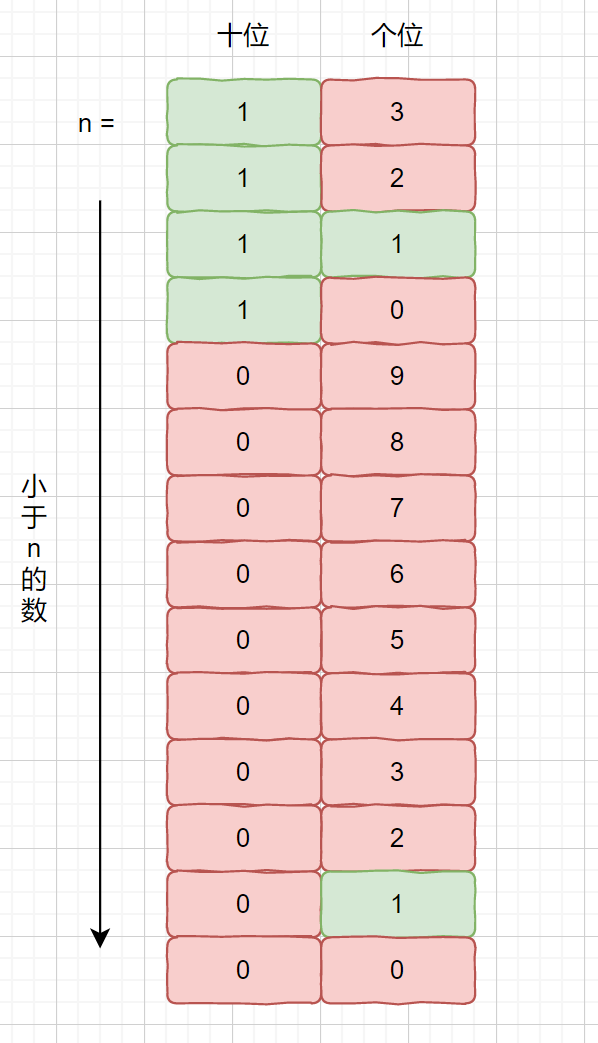
我们假设 n = 13 (用个小点的数,比较容易举例)
|
||
|
||
|
||
|
||
我们需要统计小于等于 13 的数中,出现 1 的次数,
|
||
|
||
通过上图可知,个位上 1 出现 2 次,十位上 1 出现 4 次
|
||
|
||
那么总次数为 2 + 4 = 6 次。
|
||
|
||
> 另外我们发现 11 这个数,会被统计 2 次,它的十位和个位都为 1 ,
|
||
>
|
||
> 而我们这个题目是要统计 1 出现的次数,而不是统计包含 1 的整数,所以上诉方法不会出现重复统计的情况。
|
||
>
|
||
|
||
我们题目已经有大概思路啦,下面的难点就是如何统计每一位中 1 出现的次数呢?
|
||
|
||
我们完全可以通过遍历 n 的每一位来得到总个数,见下图
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
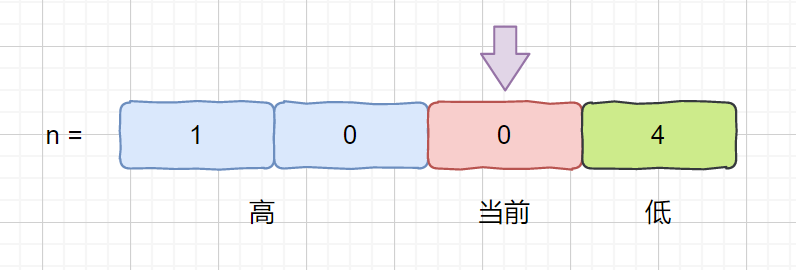
假设我们想要得到十位上 1 出现的次数,当前我们指针指向十位,
|
||
|
||
我们称之为当前位。num 则代表当前位的位因子,当前位为个位时 num = 1,十位时为 10,百位时为 100....
|
||
|
||
那我们将**当前位左边的定义为高位**,**当前位右边的定义位低位**。
|
||
|
||
> 例:n = 1004 ,此时指针指向十位(当前位)num = 10,高位为百位,千位,低位为个位
|
||
|
||
而且我们某一位的取值范围为 0 ~ 9,那么我们可以将这 10 个数分为 3 类,小于 1 (当前位数字为 0 ),等于 1(当前位数字为 1 ) ,大于 1(当前位上数字为 2 ~ 9),下面我们就来分别考虑三种情况。
|
||
|
||
> **我们进行举例的 n 为 1004,1014,1024。重点讨论十位上 3 种不同情况**。大家阅读下方文字之前,先想象自己脑子里有一个行李箱的滚轮密码锁,我们固定其中的某一位,然后可以随意滑动其他位,这样可以帮助大家理解。
|
||
>
|
||
> 注:该比喻来自与网友 ryan0414,看到的时候,不禁惊呼可太贴切了!
|
||
|
||
### **n = 1004**
|
||
|
||
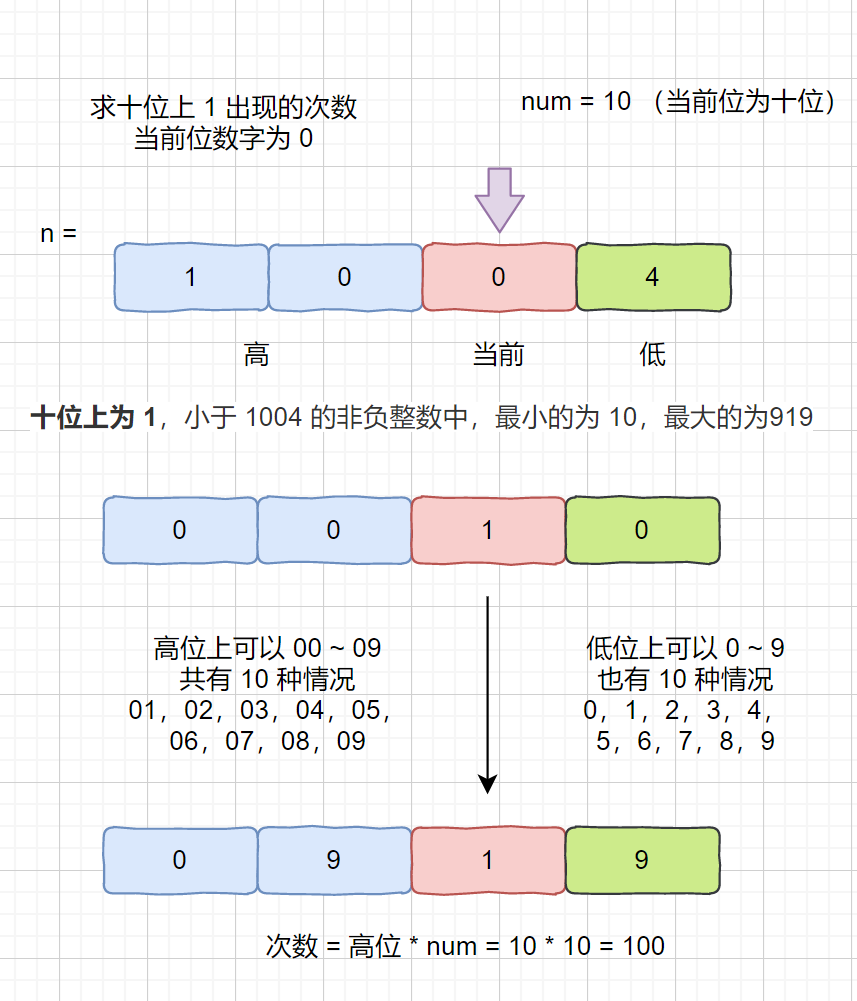
我们想要计算出**小于等于 1004 的非负整数中**,十位上出现 1 的次数。
|
||
|
||
也就是当前位为十位,数字为 0 时,十位上出现 1 的次数。
|
||
|
||
|
||
|
||
> 解析:为什么我们可以直接通过高位数字 * num,得到 1 出现的次数
|
||
>
|
||
> 因为我们高位为 10,可变范围为 0 ~ 10,但是我们的十位为 0 ,所以高位为 10 的情况取不到,所以共有 10 种情况。
|
||
>
|
||
> 又当前位为十位,低位共有 1 位,可选范围为 0 ~ 9 共有 10 种情况,所以直接可以通过 10 * 10 得到。
|
||
|
||
其实不难理解,我们可以设想成行李箱的密码盘,在一定范围内,也就是上面的 0010 ~ 0919 , 固定住一位为 1 ,只能移动其他位,看共有多少种组合。
|
||
|
||
好啦,这个情况我们已经搞明白啦,下面我们看另一种情况。
|
||
|
||
### n = 1014
|
||
|
||
我们想要计算出**小于等于 1014 的非负整数中**,十位上出现 1 的次数。
|
||
|
||
也就是当前位为十位,数字为 1 时,十位上出现 1 的次数。
|
||
|
||
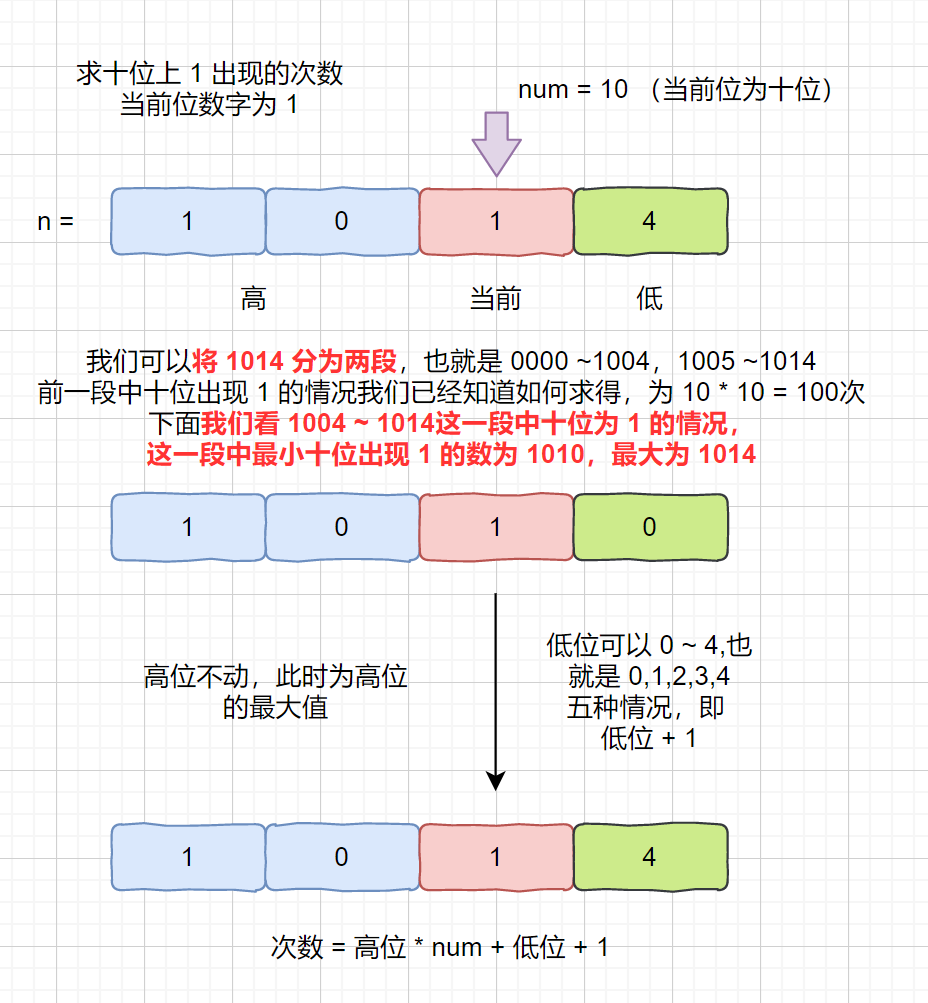
我们在小于 1014 的非负整数中,十位上为 1 的最小数字为 10,最大数字为 1014,所以我们需要在 10 ~ 1014 这个范围内固定住十位上的 1 ,移动其他位。
|
||
|
||
其实然后我们可以将 1014 看成是 1004 + 10 = 1014
|
||
|
||
则可以将 10 ~ 1014 拆分为两部分 0010 ~ 0919 (小于 1004 ),1010 ~ 1014。
|
||
|
||
见下图
|
||
|
||
|
||
|
||
> 解析:为什么我们可以直接通过 高位数字 * num + 低位数字 + 1 即 10 * 10 + 4 + 1
|
||
>
|
||
> 得到 1 出现的次数
|
||
>
|
||
> 高位数字 * num 是得到第一段的次数,第二段为 低位数字 + 1,求第二段时我们高位数字和当前位已经固定,
|
||
>
|
||
> 我们可以改变的只有低位。
|
||
|
||
可以继续想到密码盘,求第二段时,把前 3 位固定,只能改变最后一位。最后一位最大能到 4 ,那么共有几种情况?
|
||
|
||
### n = 1024
|
||
|
||
我们想要计算出**小于等于 1024 的非负整数中**,十位上出现 1 的次数。
|
||
|
||
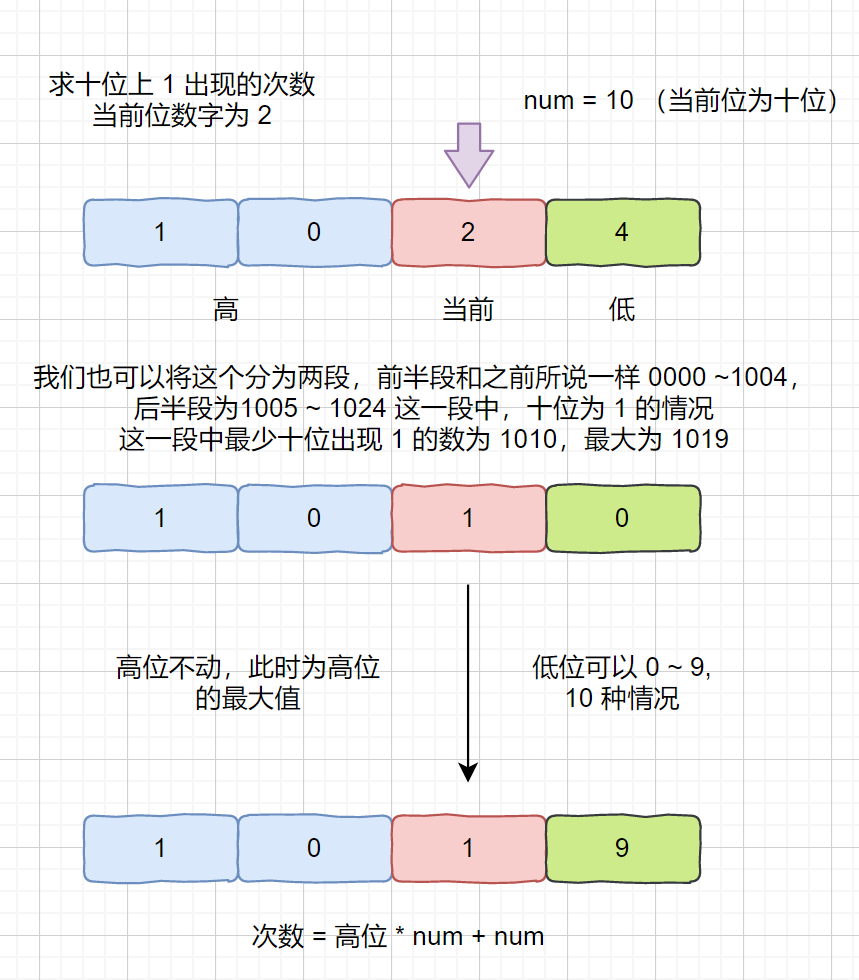
也就是当前位为十位,数字为 2 ~ 9 时,十位上出现 1 的次数。其中最小的为 0010,最大的为 1019
|
||
|
||
我们也可以将其拆成两段 0010 ~ 0919,1010 ~ 1019
|
||
|
||
|
||
|
||
|
||
|
||
> 解析:为什么我们可以直接通过高位数字 * num + num, 10 * 10 + 10 得到 1 出现的次数
|
||
>
|
||
> 第一段和之前所说一样,第二段的次数,我们此时已经固定了高位和当前位,当前位为 1,低位可以随意取值,上诉例子中,当前位为 10,低位为位数为 1,则可以取值 0 ~ 9 的任何数,则共有 10 (num) 种可能。
|
||
|
||
好啦,这个题目大家应该理解的差不多啦,
|
||
|
||
下面我们通过动画模拟一下,是怎样一步一步的计算出,小于等于 1014 的数中 1 出现的次数。
|
||
|
||
> 注:蓝色高位,橙色当前位,绿色低位
|
||
>
|
||
> 初始化:low = 0, cur = n % 10, num = 1, count = 0, high = n / 10;
|
||
|
||

|
||
|
||
|
||
|
||
好啦,下面我们看一下题目代码吧
|
||
|
||
注:下方代码没有简写,也都标有注释,大家可以结合动画边思考边阅读。
|
||
|
||
**题目代码**
|
||
|
||
```java
|
||
class Solution {
|
||
public int countDigitOne(int n) {
|
||
//高位
|
||
int high = n;
|
||
//低位
|
||
int low = 0;
|
||
//当前位
|
||
int cur = 0;
|
||
int count = 0;
|
||
int num = 1;
|
||
while (high != 0 || cur != 0) {
|
||
cur = high % 10;
|
||
high /= 10;
|
||
//这里我们可以提出 high * num 因为我们发现无论为几,都含有它
|
||
if (cur == 0) count += high * num;
|
||
else if (cur == 1) count += high * num + 1 + low;
|
||
else count += (high + 1) * num;
|
||
//低位
|
||
low = cur * num + low;
|
||
num *= 10;
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
时间复杂度 : O(logn) 空间复杂度 O(1)
|
||
|
||
|
||
|