14 KiB
这假期咋就唰的一下就没啦,昨天还跟放假第一天似的,今天就开始上班了。
既然开工了,那咱们就随遇而安呗,继续努力搬砖吧。
下面我们将镜头切到袁记菜馆。
小二:掌柜的,最近大家都在忙着种树,说是要保护环境。
老板娘:树 ? 咱们店有呀,前几年种的那棵葡萄树,不是都结果子了吗?就数你吃的最多。
小儿:这.......。
大家应该猜到,咱们今天要唠啥了。
之前给大家介绍了链表,栈,哈希表 等数据结构
今天咱们来看一种新的数据结构,树。
PS:本篇文章内容较基础,对于没有学过数据结构的同学会有一些帮助,如果你已经学过的话,也可以复习一下,查缺补漏,后面会继续更新这个系列。
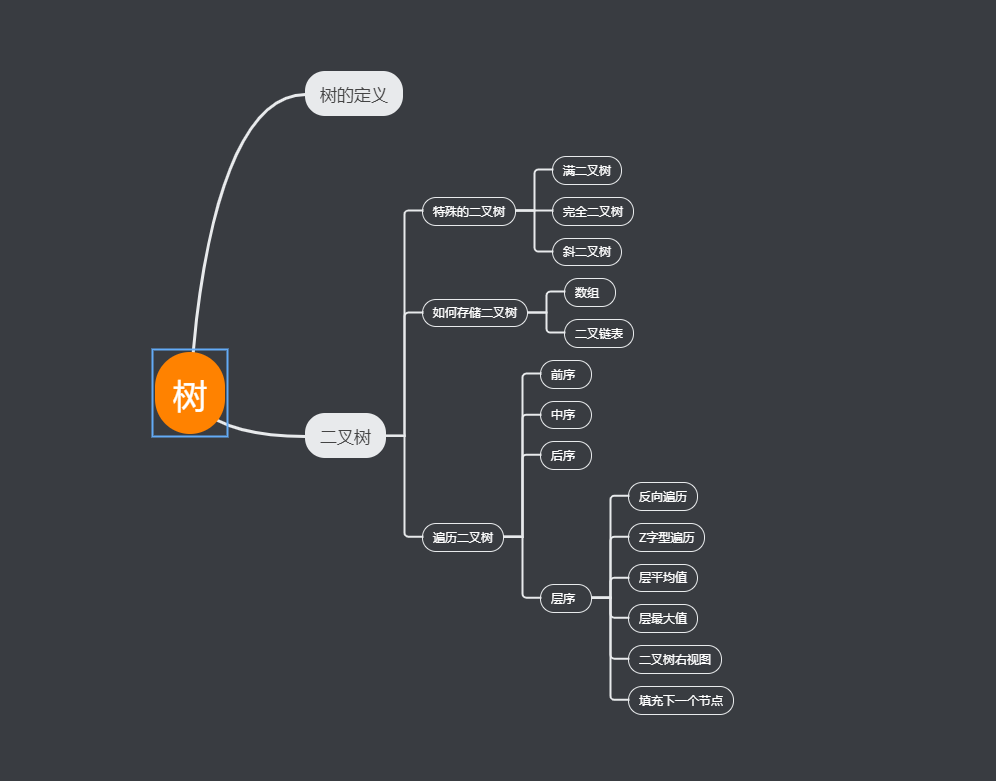
文章大纲
注:可能有的同学不喜欢手机阅读,所以将这篇同步在了我的仓库,大家可以去 Github 进行阅读,点击文章最下方的阅读原文即可
树
我们先来看下百度百科对树的定义
树是 n (n >= 0) 个节点的有限集。 n = 0 时 我们称之为空树, 空树是树的特例。
在任意一棵非空树中:
- 有且仅有一个特定的节点称为根(Root)的节点
- 当 n > 1 时,其余节点可分为 m (m > 0)个
互不相交的有限集T1、T2、........Tm,其中每一个集合本身又是一棵树,并且称为根的子树。
我们一起来拆解一下上面的两句话,到底什么是子树呢?见下图
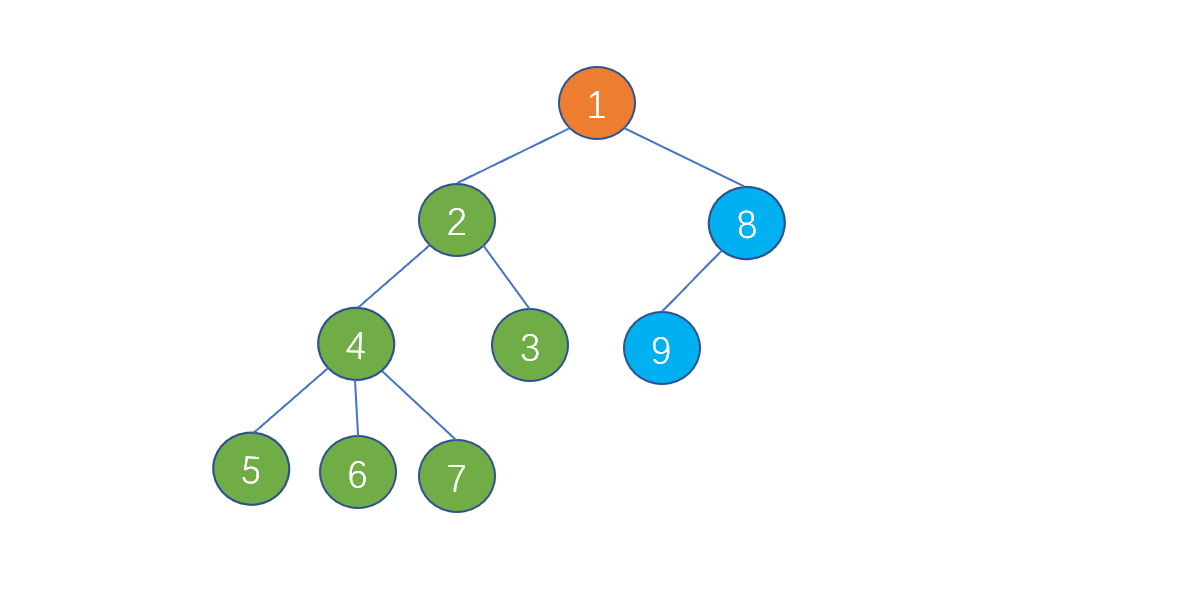
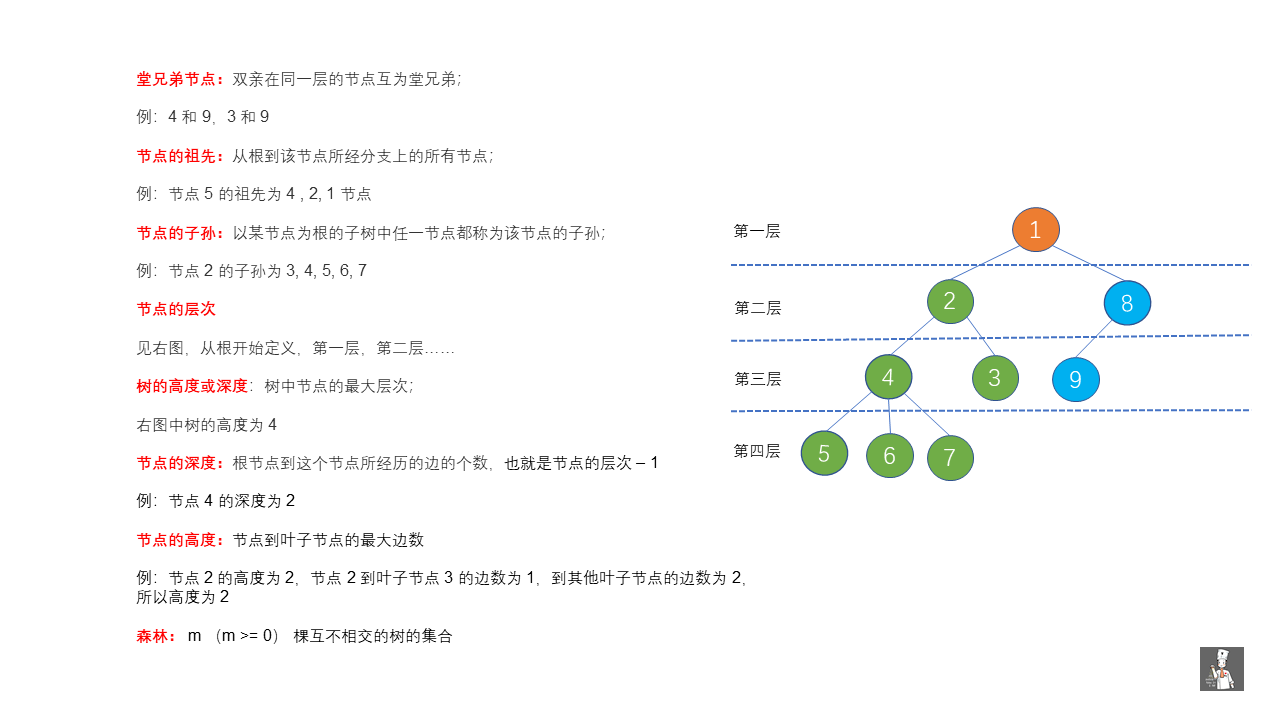
例如在上面的图中
有且仅有一个特定的节点称为根节点,也就是上图中的橙色节点。
当节点数目大于 1 时,除根节点以外的节点,可分为 m 个互不相交的有限集 T1,T2........Tm。
例如上图中,我们将根节点以外的节点,分为了 T1 (2,3,4,5,6,7),T2(8,9)两个有限集。
那么 T1 (绿色节点)和 T2(蓝色节点)就是根节点(橙色节点)的子树。
我们拆解之后发现,我们上图中的例子符合树的要求,另外不知道大家有没有注意到这个地方。
除根节点以外的节点,可分为 m 个互不相交的有限集。
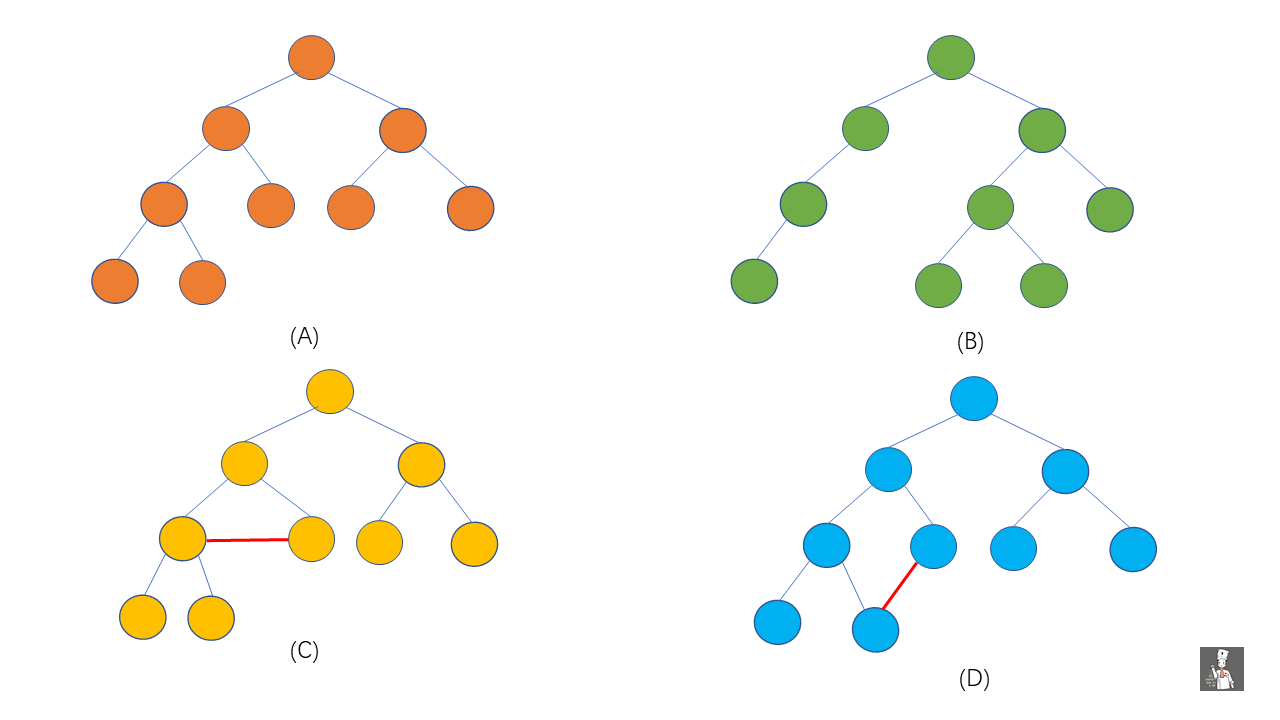
那么这个互不相交又是什么含义呢?见下图。
我们将 (A) , (B) , (C) , (D) 代入上方定义中发现,(A) , (B) 符合树的定义,(C), (D) 不符合,这是因为 (C) , (D) 它们都有相交的子树。
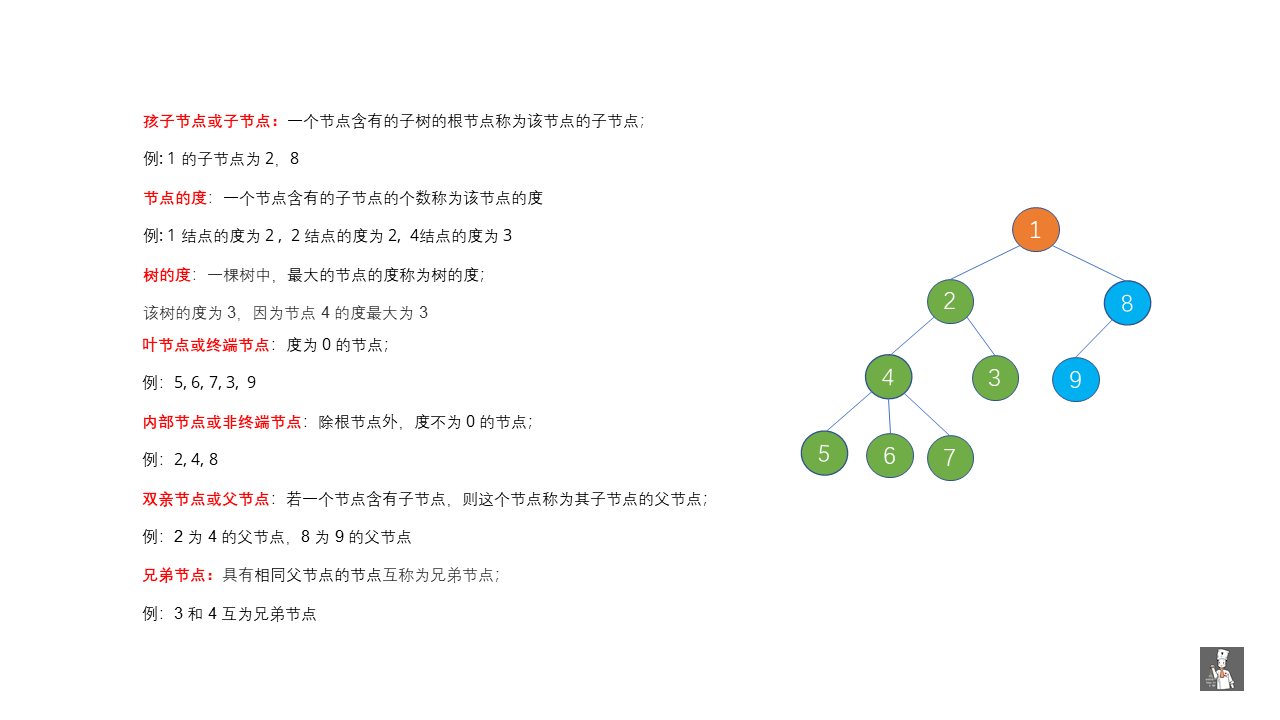
好啦,到这里我们知道如何辨别树啦,下面我们通过下面两张图再来深入了解一下树。
主要从节点类型,节点间的关系下手。
这里节点的高度和深度可能容易记混,我们代入到现实即可。
我们求深度时,从上往下测量,求高度时,从下往上测量,节点的高度和深度也是如此。
二叉树
我们刷题时遇到的就是二叉树啦,下面我们一起来了解一下二叉树
二叉树前提是一棵树,也就是需要满足我们树的定义的同时,还需要满足以下要求
每个节点最多有两个子节点,分别是左子节点和右子节点。
注意我们这里提到的是最多,所以二叉树并不是必须要求每个节点都有两个子节点,也可以有的仅有一个左子节点,有的节点仅有一个右子节点。
下面我们来总结一下二叉树的特点
- 每个节点最多有两棵子树,也就是说二叉树中不存在度大于 2 的节点,节点的度可以为 0,1,2。
- 左子树和右子树是有顺序的
- 假如只有一棵子树 ,也要区分它是左子树还是右子树
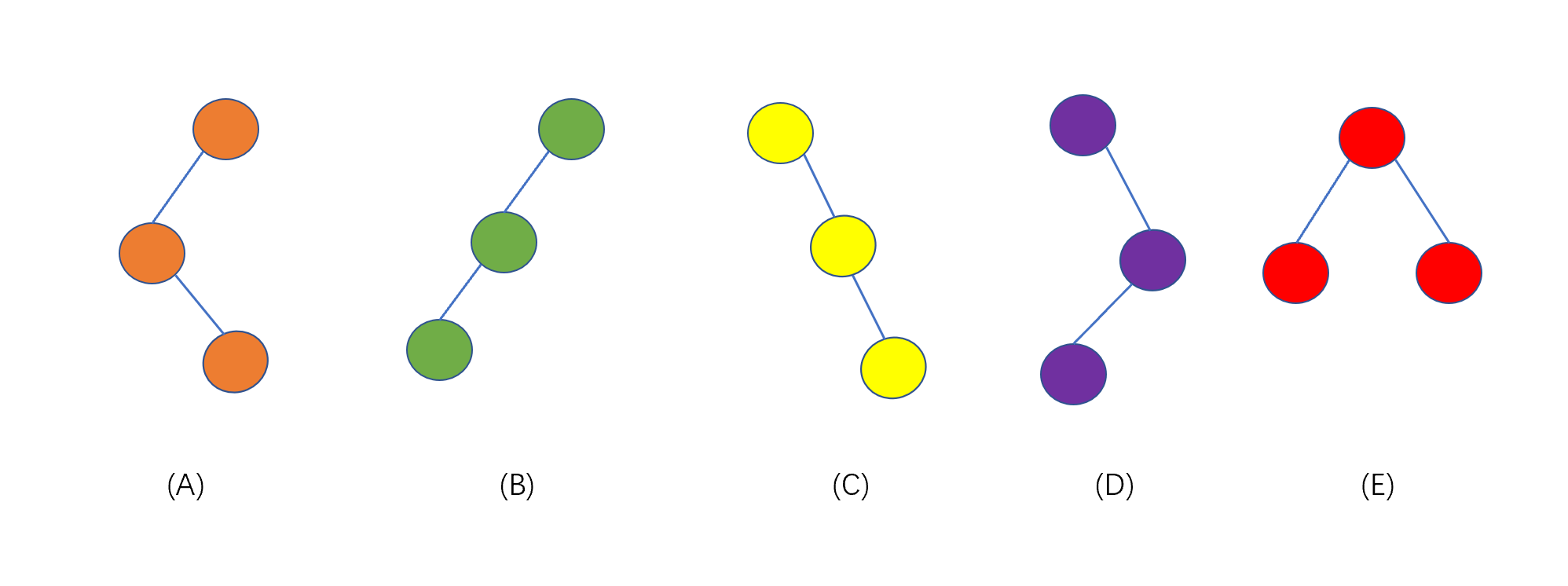
好啦,我们已经了解了二叉树的特点,那我们分析一下,下图中的树是否满足二叉树定义,共有几种二叉树。
上图共为 5 种不同的二叉树,在二叉树的定义中,二叉树的左子树和右子树是有顺序的,所以上图为 5 种不同的二叉树。
特殊的二叉树
下面我们来说几种比较特殊的二叉树,可以帮助我们刷题时,考虑到特殊情况。
满二叉树
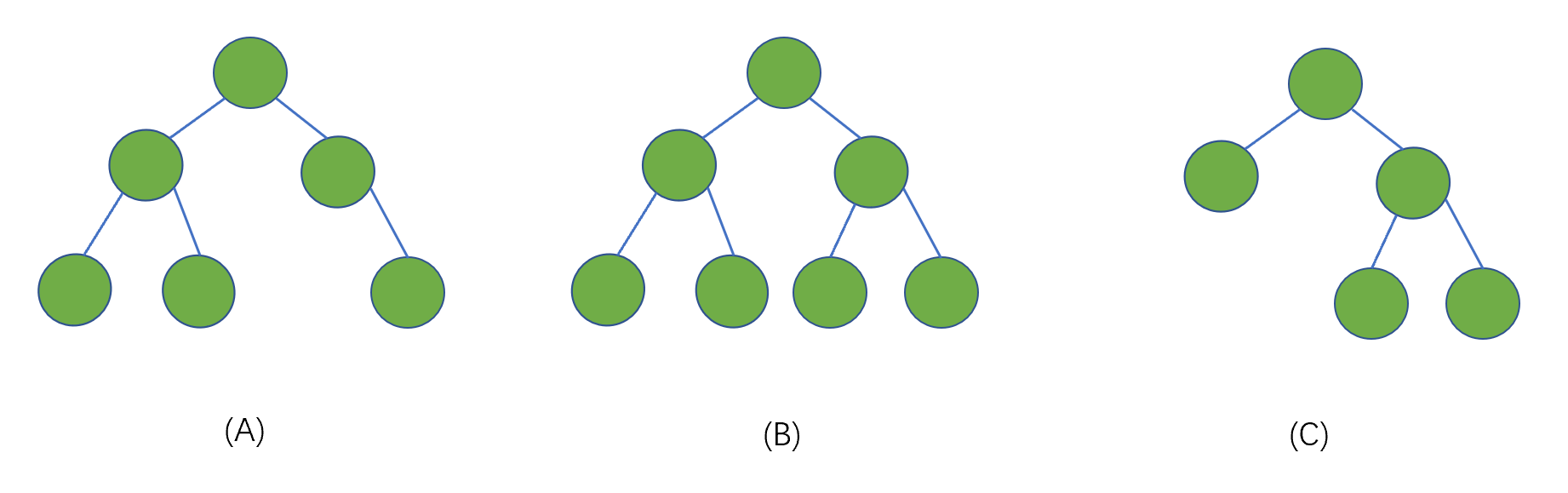
满二叉树:在一棵二叉树中,所有分支节点都存在左子树和右子树,并且所有的叶子都在同一层,这种树我们称之为完全二叉树.见下图
我们发现只有 (B) 符合满二叉树的定义,我们发现其实满二叉树也为完全二叉树的一种
完全二叉树
完全二叉树:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
哦!我们可以这样理解,除了最后一层,其他层的节点个数都是满的,而且最后一层的叶子节点必须靠左。
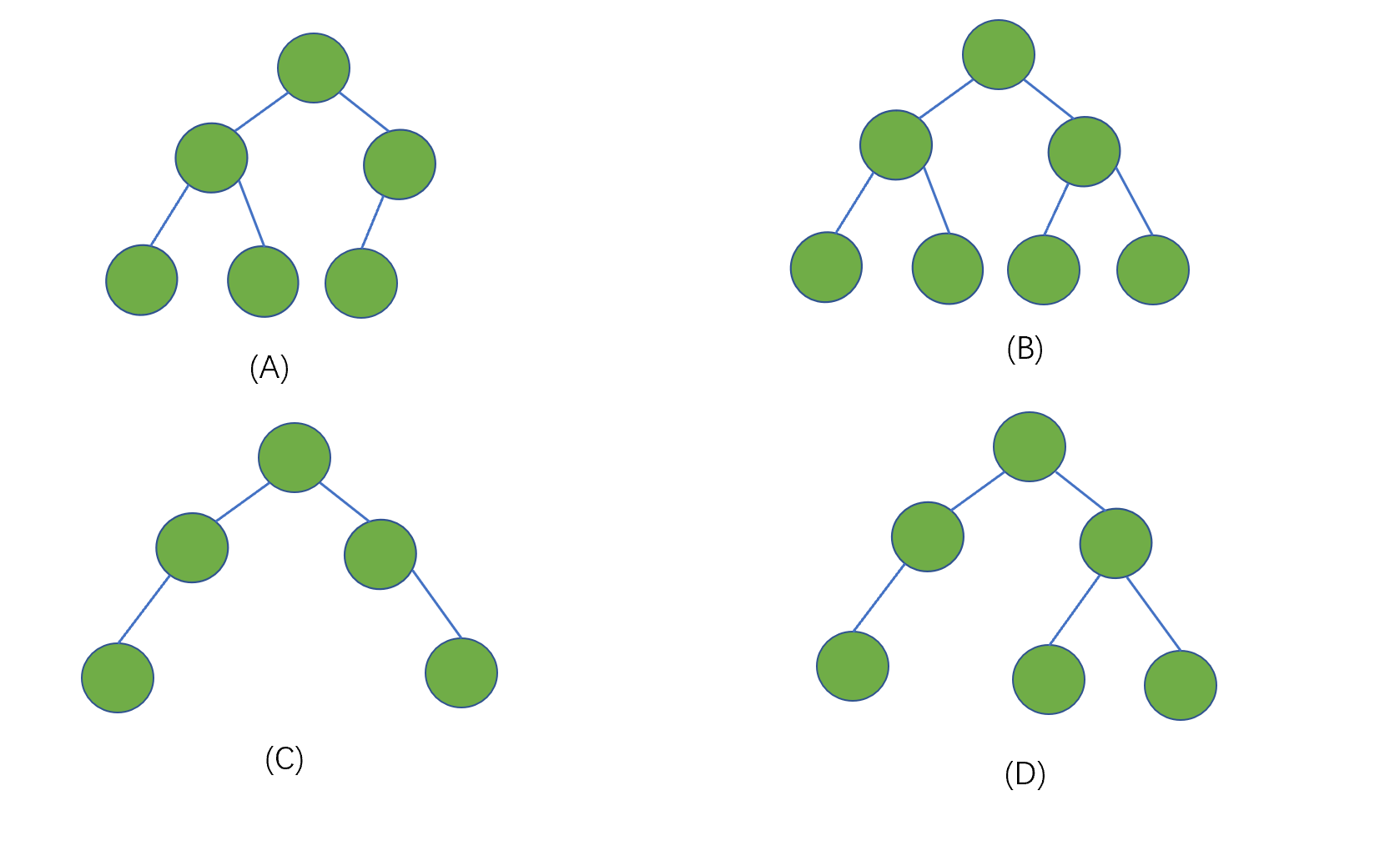
下面我们来看一下这几个例子
上面的几个例子中,(A)(B)为完全二叉树,(C)(D)不是完全二叉树
斜二叉树
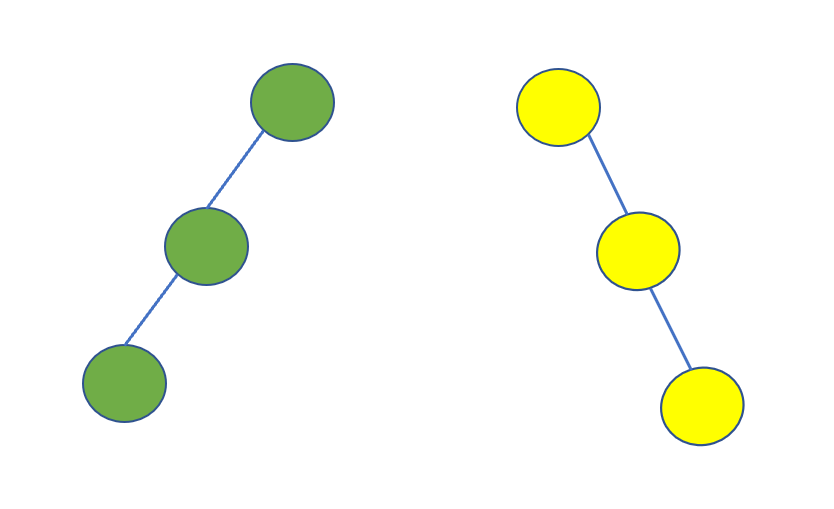
这个就很好理解啦,斜二叉树也就是斜的二叉树,所有的节点只有左子树的称为左斜树,所有节点只有右子树的二叉树称为右斜树.
诺,下面这俩就是.
另外还有 一些二叉树的性质, 比如第 i 层至多有多少节点,通过叶子节点求度为 2 的节点, 通过节点树求二叉树的深度等, 这些是考研常考的知识,刷题时一般不太用到, 所以不在这里赘述,需要的同学可以看一下王道或者天勤的数据结构, 上面描述的很具体, 并附有证明过程.
如何存储二叉树
二叉树多采用两种方法进行存储,基于数组的顺序存储法和基于指针的二叉链式存储法
我们在之前说过的堆排序中,其中对堆的存储采用的则是顺序存储法,具体细节可以看这篇文章
一个破堆排我搞了 4 个动画?
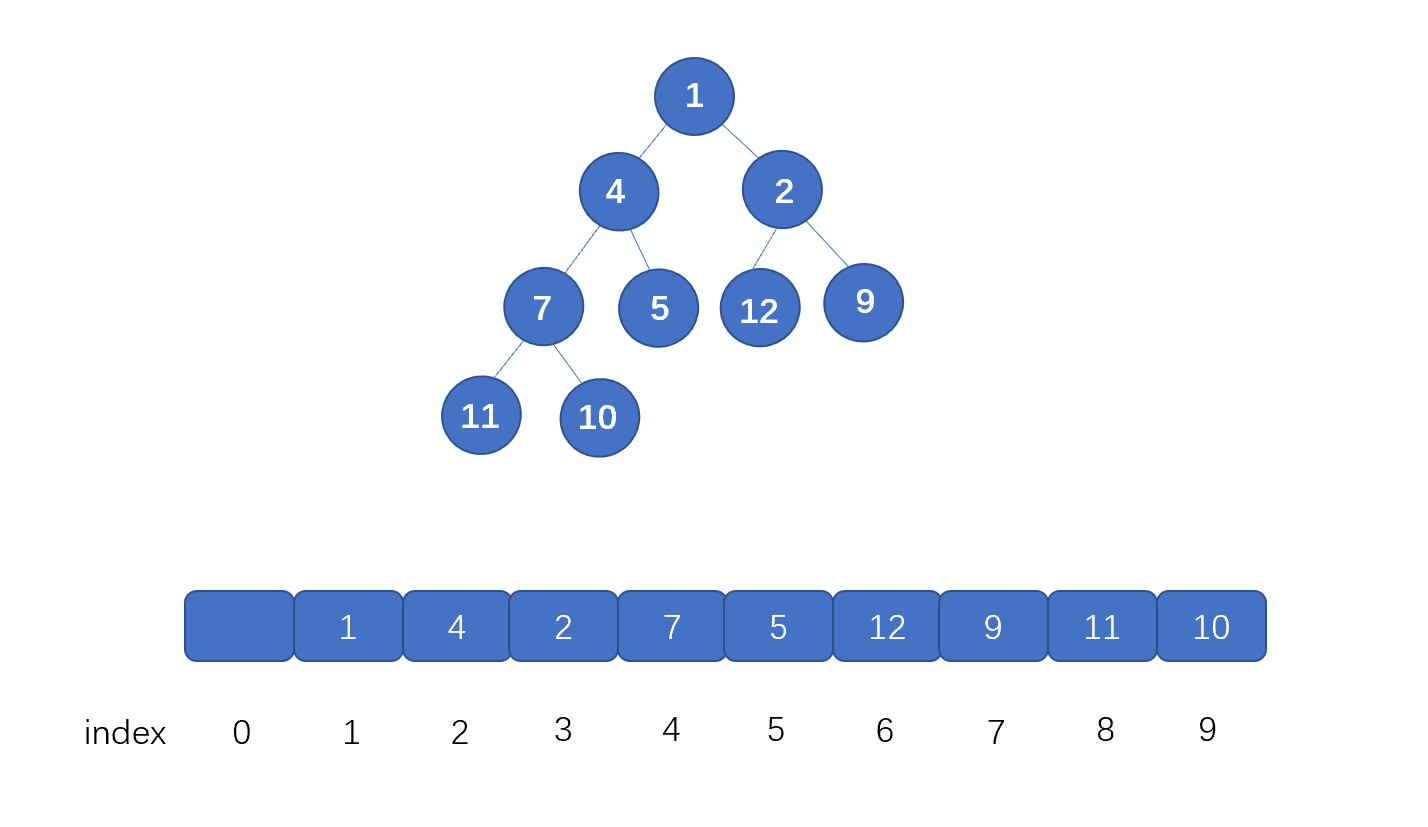
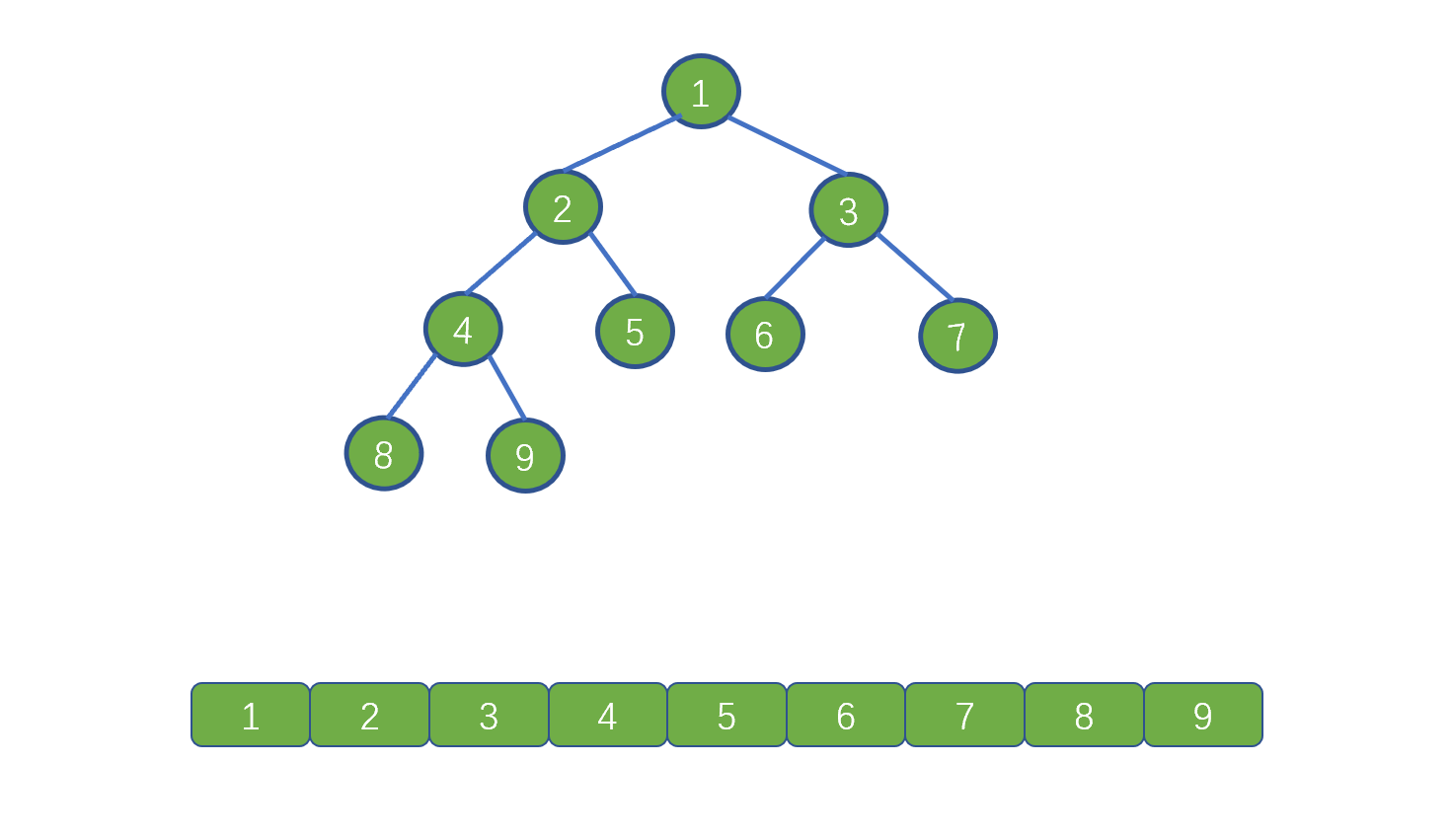
这里我们再来说一下如何用数组存储完全二叉树.
我们首先看根节点,也就是值为 1 的节点,它在数组中的下标为 1 ,它的左子节点,也就是值为 4 的节点,此时索引为 2,右子节点也就是值为 2 的节点,它的索引为 3。
我们发现其中的关系了吗?
数组中,某节点(非叶子节点)的下标为 i , 那么其左子节点下标为 2*i (这里可以直接通过相乘得到左孩子, 也就是为什么空出第一个位置, 如果从 0 开始存,则需要 2i+1 才行), 右子节点为 2i+1,其父节点为 i/2 。既然我们完全可以根据索引找到某节点的 左子节点 和 右子节点,那么我们用数组存储是完全没有问题的。
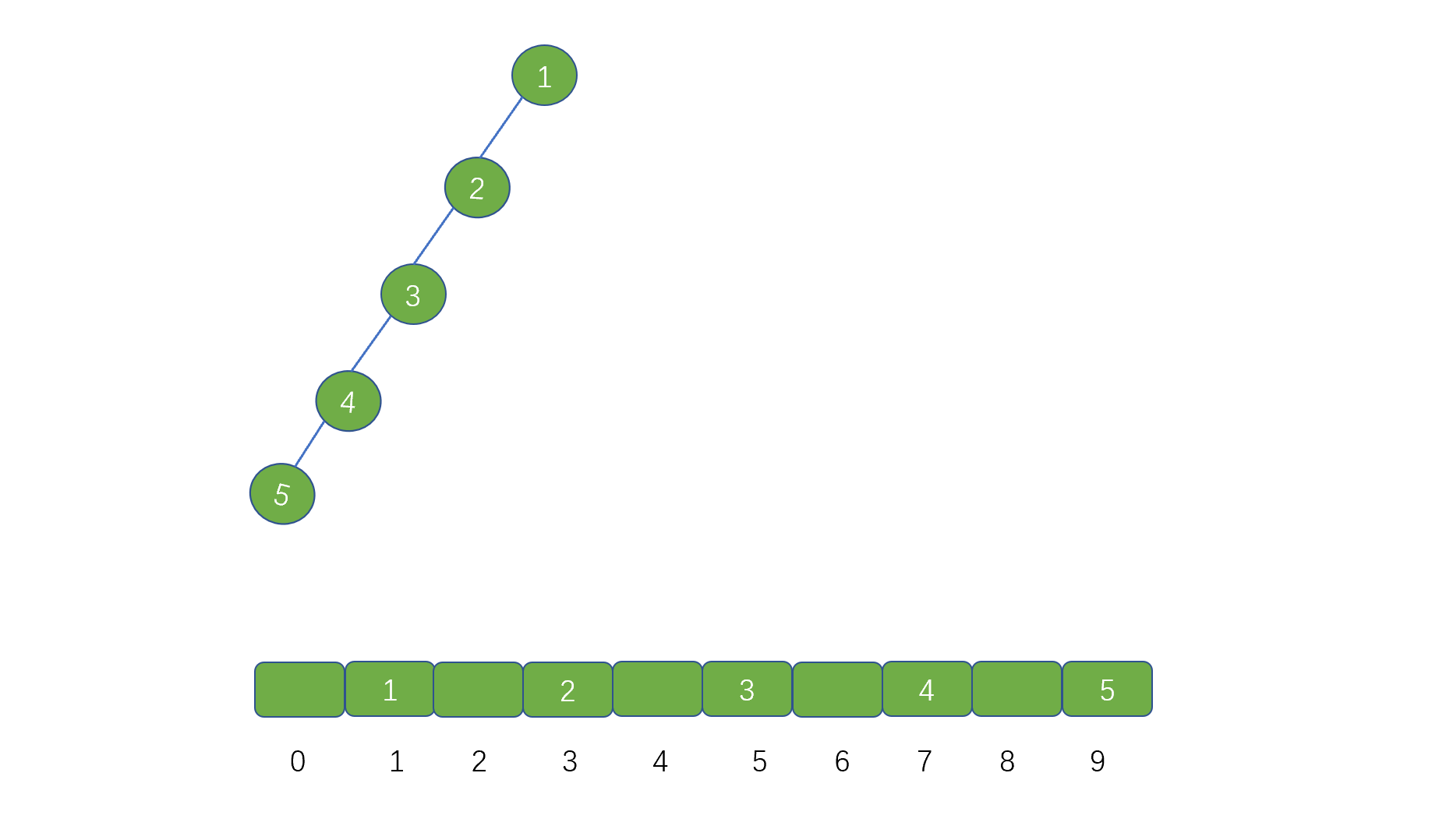
但是,我们再考虑一下这种情景,如果我们用数组存储斜树时会出现什么情况?
通过 2*i 进行存储左子节点的话,如果遇到斜树时,则会浪费一半的存储空间,这样显然是不合适的,
所以说当存储完全二叉树时,我们用数组存储,无疑是最省内存的
所以我们下面介绍一下另一种存储结构,链式存储结构.
因为二叉树的每个节点, 最多有两个孩子, 所以我们只需为每个节点定义一个数据域,两个指针域即可
val 为节点的值, left 指向左子节点, right 指向右子节点.
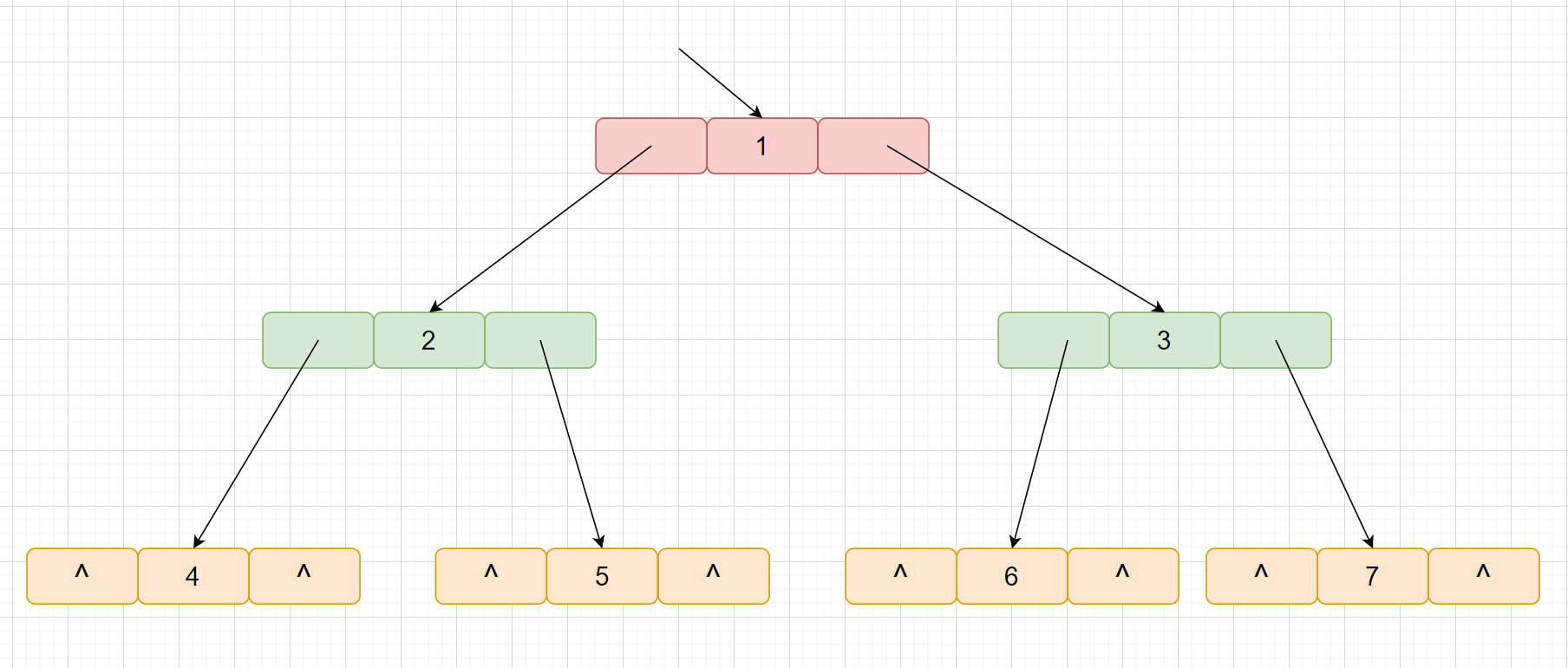
下面我们对树 1, 2, 3, 4, 5, 6, 7 使用链式存储结构进行存储,即为下面这种情况.
二叉链表的节点结构定义代码
public class BinaryTree {
int val;
BinaryTree left;
BinaryTree right;
BinaryTree() {}
BinaryTree(int val) { this.val = val; }
BinaryTree(int val, BinaryTree left, BinaryTree right) {
this.val = val;
this.left = left;
this.right = right;
}
}
另外我们在刷题的时候, 可以自己实现一下数据结构, 加深我们的理解, 提升基本功, 而且面试考的也越来越多.
好啦,下面我们说一下树的遍历,
下面我会用动图的形式进行描述,很容易理解, 我也会为大家总结对应的题目, 题目对应的代码我会放到我的仓库,欢迎各位阅读.
遍历二叉树
二叉树的遍历指从根节点出发,按照某种次序依次访问二叉树的所有节点,使得每个节点都被访问且访问一次.
我们下面介绍二叉树的几种遍历方法及其对应的题目, 前序遍历, 中序遍历 , 后序遍历 , 层序遍历 .
前序遍历
前序遍历的顺序是, 对于树中的某节点,先遍历该节点,然后再遍历其左子树,最后遍历其右子树.
只看文字有点生硬, 下面我们直接看动画吧
测试题目: leetcode 144. 二叉树的前序遍历
代码实现(递归版)
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> arr = new ArrayList<>();
preorder(root,arr);
return arr;
}
public void preorder(TreeNode root,List<Integer> arr) {
if (root == null) {
return;
}
arr.add(root.val);
preorder(root.left,arr);
preorder(root.right,arr);
}
}
时间复杂度 : O(n) 空间复杂度 : O(n) 为递归过程中栈的开销,平均为 O(logn),但是当二叉树为斜树时则为 O(n)
为了控制文章篇幅, 二叉树的迭代遍历形式, 会在下篇文章进行介绍
中序遍历
中序遍历的顺序是, 对于树中的某节点,先遍历该节点的左子树, 然后再遍历该节点, 最后遍历其右子树
继续看动画吧, 如果有些遗忘或者刚开始学数据结构的同学可以自己模拟一下执行步骤.
测试题目: leetcode 94 题 二叉树的中序遍历
代码实现(递归版)
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
public void inorder (TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
时间复杂度 : O(n) 空间复杂度 : O(n)
后序遍历
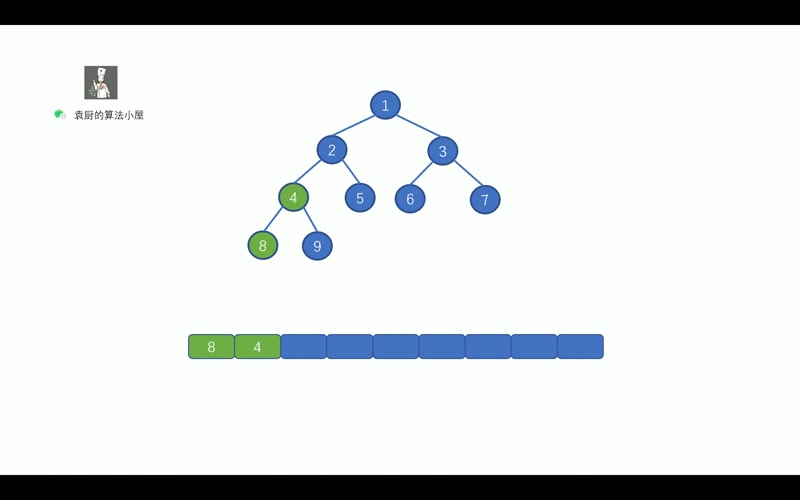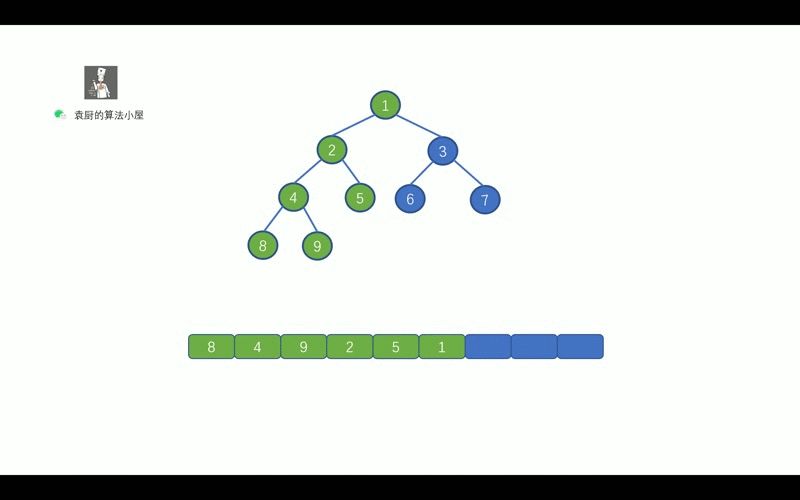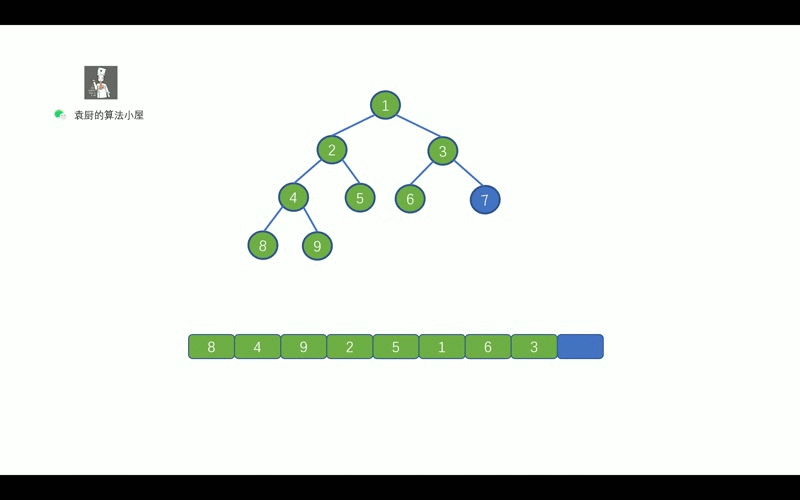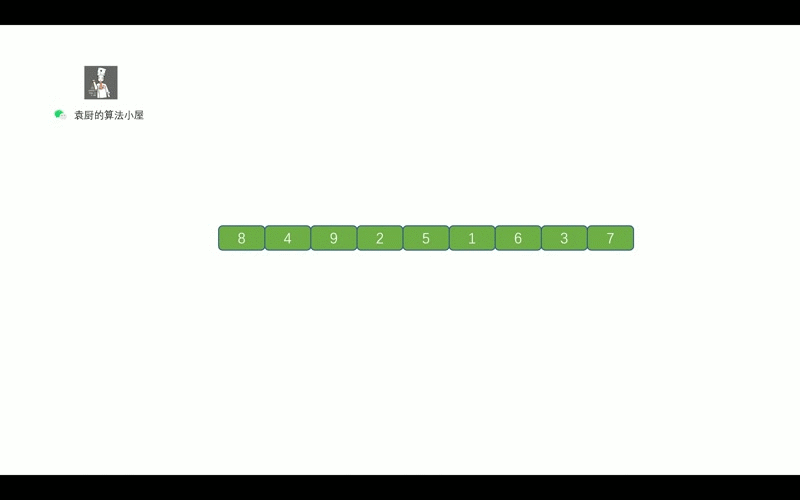
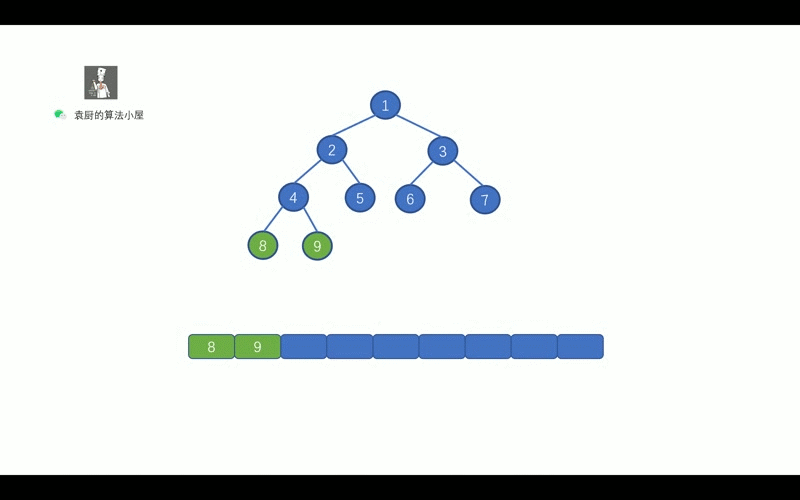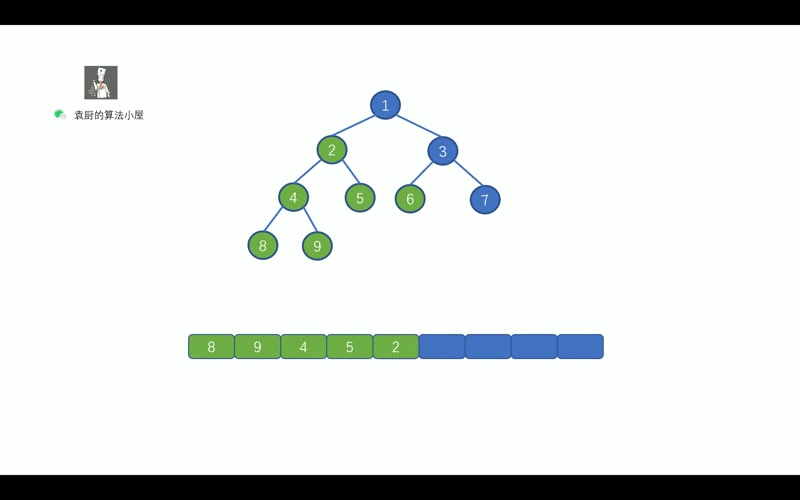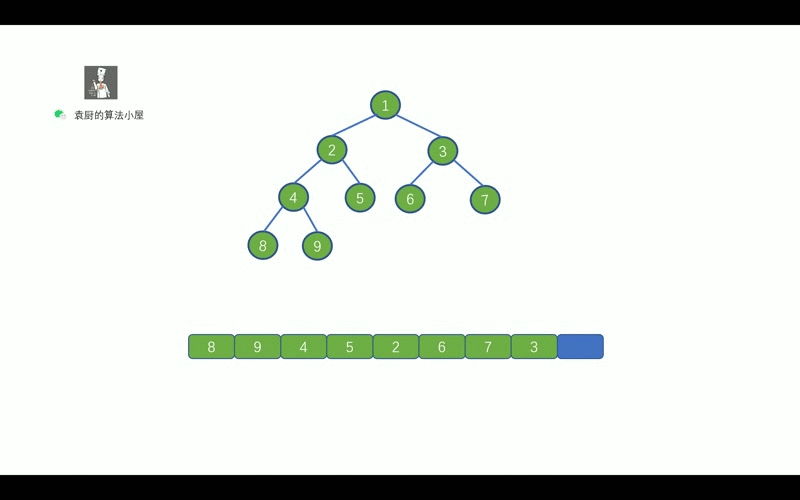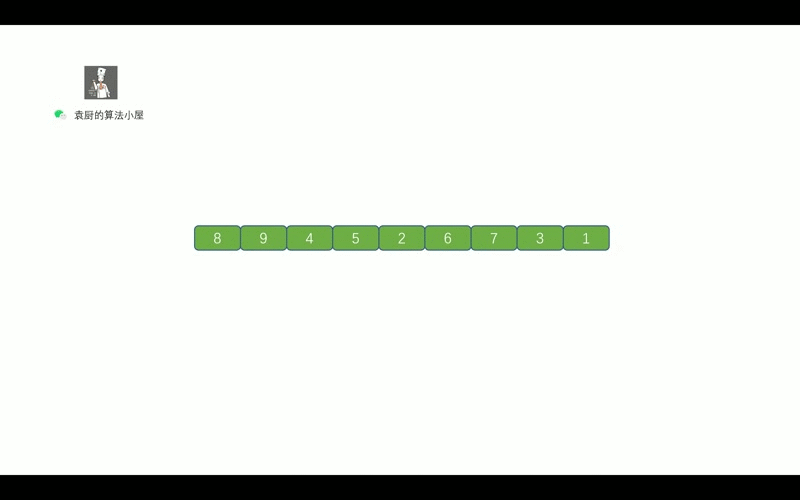
后序遍历的顺序是, 对于树中的某节点, 先遍历该节点的左子树, 再遍历其右子树, 最后遍历该节点.
哈哈,继续看动画吧,看完动画就懂啦.
测试题目: leetcode 145 题 二叉树的后序遍历
代码实现(递归版)
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root,res);
return res;
}
public void postorder(TreeNode root, List<Integer> res) {
if (root == null) {
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
}
时间复杂度 : O(n) 空间复杂度 : O(n)
层序遍历
顾名思义,一层一层的遍历.
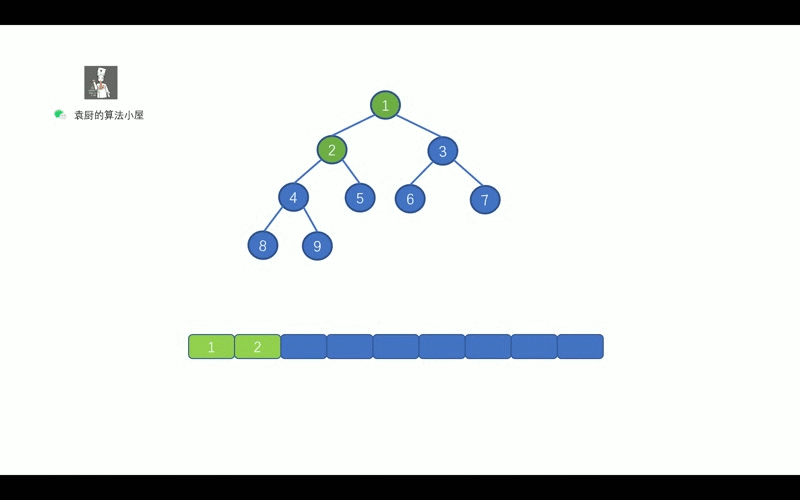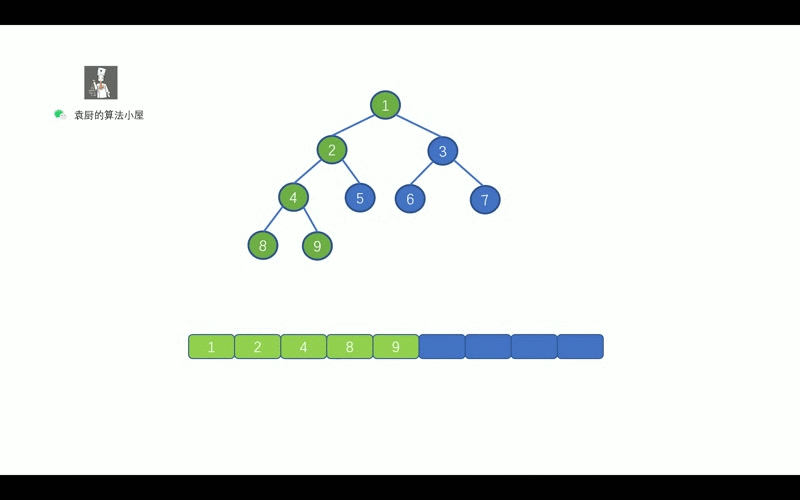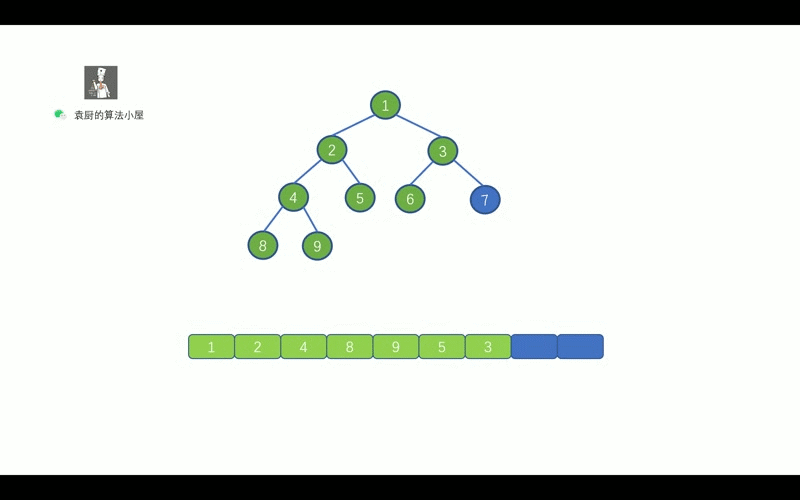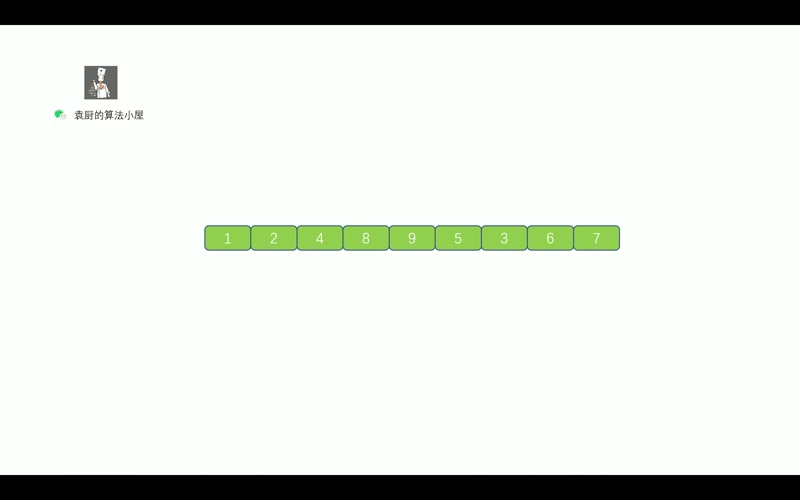
比如刚才那棵二叉树的层序遍历序列即为 1 ~ 9.
二叉树的层序, 这里我们需要借助其他数据结构来实现, 我们思考一下, 我们需要对二叉树进行层次遍历, 从上往下进行遍历, 我们可以借助什么数据结构来帮我们呢 ?
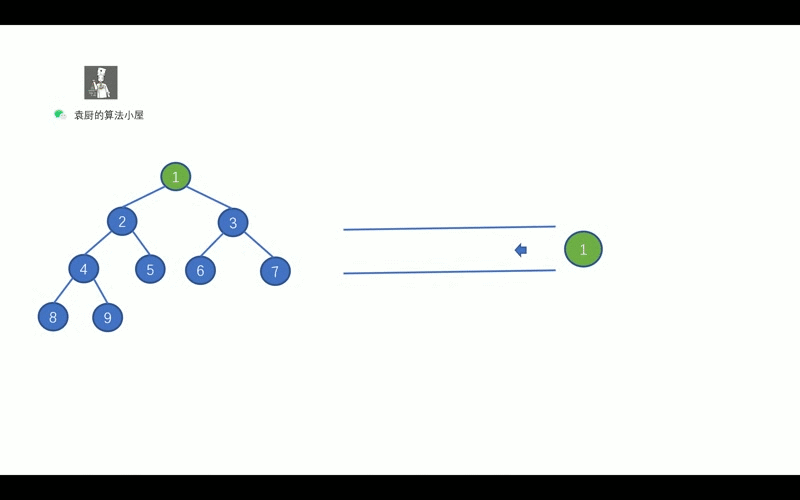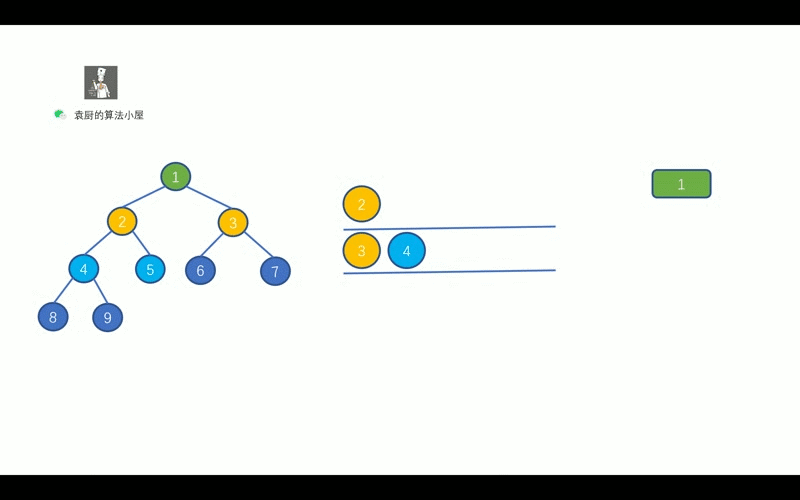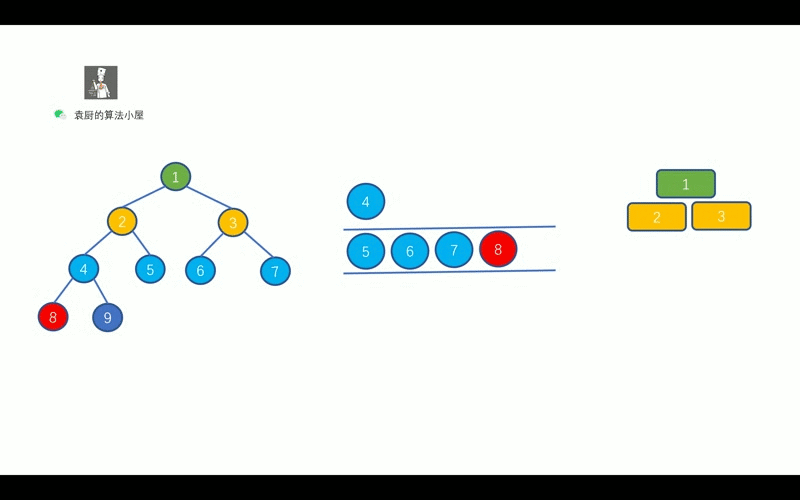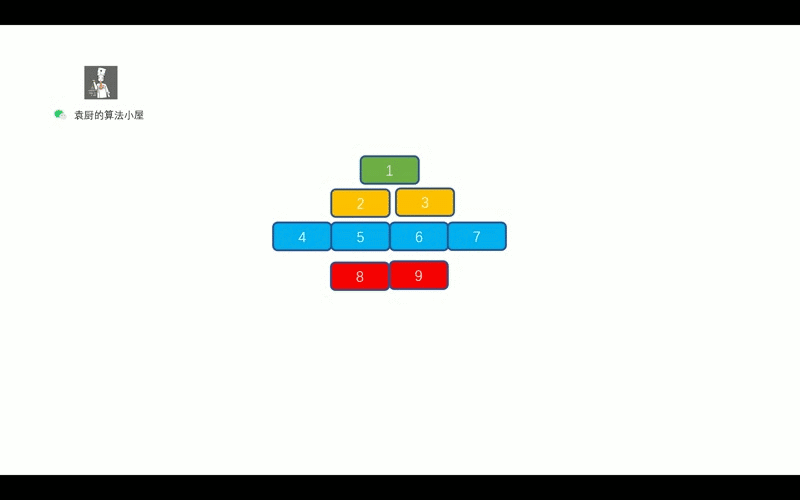
我们可以使用队列, 具体操作如下
让二叉树的每一层入队, 然后再依次执行出队操作,
对该层节点执行出队操作时, 需要将该节点的左孩子节点和右孩子节点进行入队操作,
这样当该层的所有节点出队结束后, 下一层也就入队完毕,
不过我们需要考虑的就是, 我们需要通过一个变量来保存每一层节点的数量.
这样做是为了防止, 一直执行出队操作, 使输出不能分层
好啦,下面我们直接看动画吧,
测试题目: leetcode 102 二叉树的层序遍历
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
//入队 root 节点,也就是第一层
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> list = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; ++i) {
TreeNode temp = queue.poll();
//孩子节点不为空,则入队
if (temp.left != null) queue.offer(temp.left);
if (temp.right != null) queue.offer(temp.right);
list.add(temp.val);
}
res.add(list);
}
return res;
}
}
时间复杂度:O(n) 空间复杂度:O(n)
大家如果吃透了二叉树的层序遍历的话,可以顺手把下面几道题目解决掉,思路一致,甚至都不用拐弯
-
leetcode 107. 二叉树的层序遍历 II
-
leetcode 103. 二叉树的锯齿形层序遍历
上面两道题仅仅是多了翻转
- leetcode 199. 二叉树的右视图
- leetcode 515. 在每个树行中找最大值
- leetcode 637. 二叉树的层平均值
这三道题,仅仅是加了一层的一些操作
- leetcode 116 填充每个节点的下一个右侧
- leetcode 117 填充每个节点的下一个右侧2
这两个题对每一层的节点进行链接即可。
大家可以去顺手解决这些题目,但是也要注意一下其他解法,把题目吃透。不要为了数目而刷题,好啦,今天的节目就到这里啦,我们下期见!