mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-12-29 05:46:17 +00:00
103 lines
4.5 KiB
Java
103 lines
4.5 KiB
Java
我们之前介绍了计数排序,大家应该已经完全搞定了吧,
|
||
|
||
趁着今天没啥大事咱们再来搞点其他的,如果忘记计数排序的彦祖可以先去复习一下
|
||
|
||
大家还记不记得咱们上回说的,我们的计数排序在数字范围较小,且全为整数时才可以使用,
|
||
|
||
但是当我们遇到 double 类型的数怎么办呢?
|
||
|
||
例如每日温度,26.2, 21.2, 19.8 等
|
||
|
||
所以我们今天来学一个新的线性排序算法,大家继续往下看吧
|
||
|
||
假设我们需要对本周(假设今天周日)的温度进行排序,温度分别为
|
||
|
||
16.3,20.1,17.2,16.8,15.3,19.3,18.5
|
||
|
||
我们需要对本周温度进行排序,我们当然可以使用我们之前说过的快速排序和归并排序等,
|
||
|
||
不过这里我们介绍一种我们之前没有说过的排序算法,**桶排序**。
|
||
|
||
|
||
|
||
桶,盛水或其他东西的器具。。。,哎嘛跑偏了,那么我们今天说的桶排序的桶,又是什么概念呢?
|
||
|
||
我们这里的每个桶代表一个区间范围,我们将要排序的数据分到几个有序的桶里,
|
||
|
||
然后再对桶内元素单独进行排序。排序之后,再把每个桶的桶内元素按照顺序依次取出,
|
||
|
||
最后得到的序列就是有序的啦。
|
||
|
||
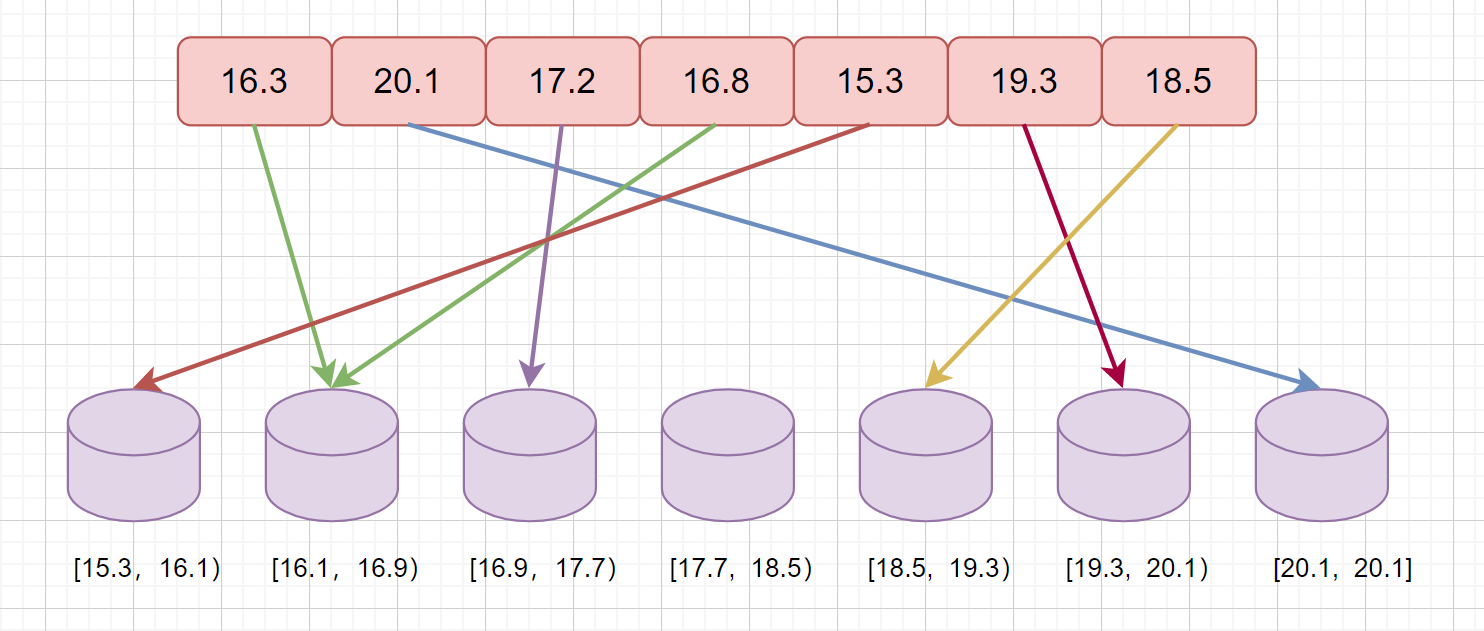
见下图,我们将元素放到对应的桶中
|
||
|
||
|
||
|
||
上图表示每个元素对应的桶,然后我们将其放入对应的桶中。
|
||
|
||

|
||
|
||
将桶内元素排序
|
||
|
||

|
||
|
||
看到这里是不是就悟啦,下一步,我们再将桶内的每个元素取出,就能够得到有序序列啦。
|
||
|
||
即
|
||
|
||
15.3,16.3,16.8,17.2,18.5,19.3,20.1
|
||
|
||
我们这里桶的数量根据元素的个数来设定,几个元素几个桶。
|
||
|
||
例如上图中,我们共有 7 个元素,则设置 7 个桶
|
||
|
||
然后我们每个桶的区间这样定义(当然也可以使用其他方法),因为我们桶的数量等于元素数量,所以我们每个区间这样设定
|
||
|
||
除了最后一个桶只包含最大值,其余桶的区间为
|
||
|
||
区间大小 = (最大值-最小值)/ (桶的数量-1)
|
||
|
||
例如:(20.1-15.3) / (7-1) = 0.8
|
||
|
||
那我们又有问题啦,我们将元素放到合适的桶之后,那么桶内元素是怎样进行保存的?并且桶内元素是如何进行排序的。
|
||
|
||
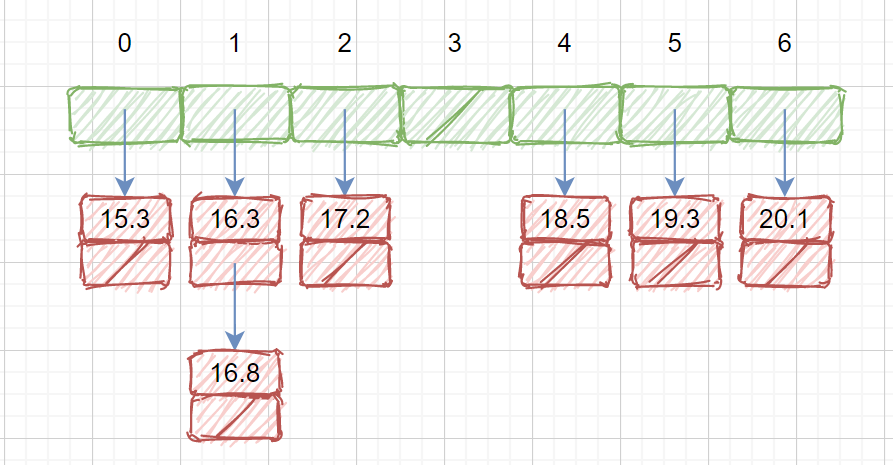
这里我们借用算法导论的方法。我们桶内元素使用链表进行保存,和我们之前说过的哈希表处理冲突时使用链地址法类似。
|
||
|
||
对桶内元素进行排序时,我们使用插入排序。(很多文章都写错了这里)
|
||
|
||
|
||
|
||
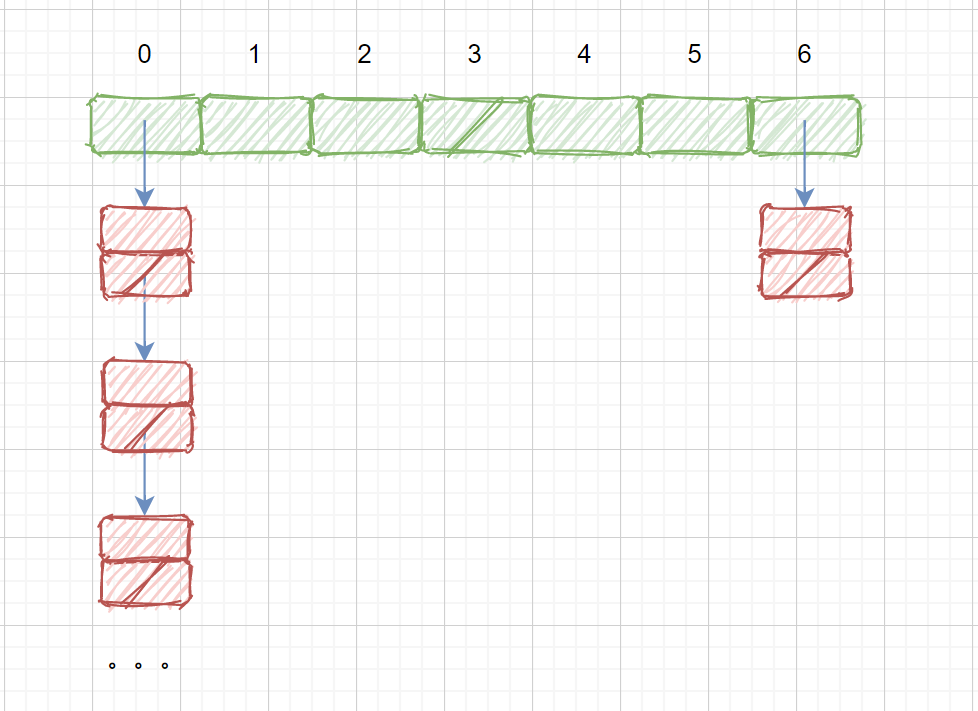
那么桶排序是完全适用于任何情况的吗?当然不是,我们思考下这种情况
|
||
|
||
|
||
|
||
此时我们元素值差距太大时,则会产生这种情况,此时效率几乎退化成了链表的插入排序,所以我们的桶排序也不是完全使用于所有情况的。所以遇到不同情况时选择合适的排序算法才是最重要的。
|
||
|
||
**桶排序的时间复杂度分析**
|
||
|
||
桶排序可以在线性时间内完成排序,即使桶内排序使用插入排序,具体证明过程可以看下算法导论 p202
|
||
|
||
**桶排序的空间复杂度分析**
|
||
|
||
桶排序使用了辅助空间所以空间复杂度为 O(n)
|
||
|
||
**桶排序的稳定性分析**
|
||
|
||
桶内使用的是链表的插入排序,所以桶排序是稳定的排序算法
|
||
|
||
好啦,是不是一下就搞懂了,今天的文章就到这里啦,大家如果觉得还不错的话就叫我一声彦祖吧。
|
||
|
||
因为这个算法面试时不会让我们手写,所以我们了解下具体含义即可,有需要代码的可以私信我,我发给你。
|
||
|
||
感谢各位老哥支持,我会继续加油的。
|
||
|
||
不过我们还有一个问题,那就是我们遍历到一个新元素时,如何知道他应该在哪个桶呢 ?
|
||
|
||
我们这样求得。
|
||
|
||
```java
|
||
(int) ((array[i] - min)/w * (bucketNum-1));
|
||
// w = max - min
|
||
```
|
||
|
||
好啦,大致含义我们就搞定啦,另外桶排序的原理很容易理解,但是代码不是特别容易实现,大家可以选择性阅读。
|