mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-01 17:53:39 +00:00
96 lines
3.8 KiB
Markdown
96 lines
3.8 KiB
Markdown
|
||
|
||
**题目描述**
|
||
|
||
今天,书店老板有一家店打算试营业 customers.length 分钟。每分钟都有一些顾客(customers[i])会进入书店,所有这些顾客都会在那一分钟结束后离开。
|
||
|
||
在某些时候,书店老板会生气。 如果书店老板在第 i 分钟生气,那么 grumpy[i] = 1,否则 grumpy[i] = 0。 当书店老板生气时,那一分钟的顾客就会不满意,不生气则他们是满意的。
|
||
|
||
书店老板知道一个秘密技巧,能抑制自己的情绪,可以让自己连续 X 分钟不生气,但却只能使用一次。
|
||
|
||
请你返回这一天营业下来,最多有多少客户能够感到满意的数量。
|
||
|
||
|
||
示例:
|
||
|
||
> 输入:customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], X = 3
|
||
> 输出:16
|
||
|
||
解释:
|
||
书店老板在最后 3 分钟保持冷静。
|
||
感到满意的最大客户数量 = 1 + 1 + 1 + 1 + 7 + 5 = 16.
|
||
|
||
|
||
|
||
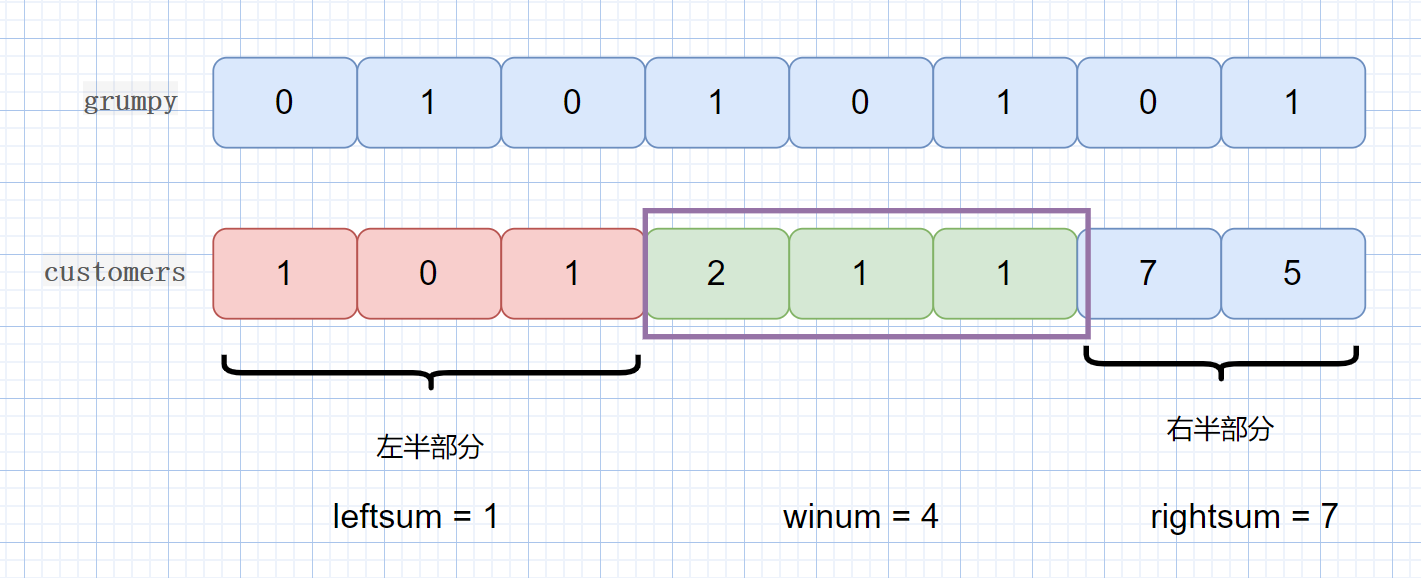
该题目思想就是,我们将 customer 数组的值分为三部分, leftsum, winsum, rightsum。我们题目的返回值则是三部分的最大和。
|
||
|
||
注意这里的最大和,我们是怎么计算的。
|
||
|
||
|
||
|
||
winsum 是窗口内的所有值,不管 grumpy[i] 的值是 0 还是 1,窗口的大小,就对应 K 的值,也就是老板的技能发动时间,该时间段内,老板不会生气,所以为所有的值。
|
||
|
||
leftsum 是窗口左边区间的值,此时我们不能为所有值,只能是 grumpy[i] == 0 时才可以加入,因为此时不是技能发动期,老板只有在 grumpy[i] == 0 时,才不会生气。
|
||
|
||
rightsum 是窗口右区间的值,和左区间加和方式一样。那么我们易懂一下窗口,我们的 win 值和 leftsum 值,rightsum 值是怎么变化的呢?
|
||
|
||
见下图
|
||
|
||
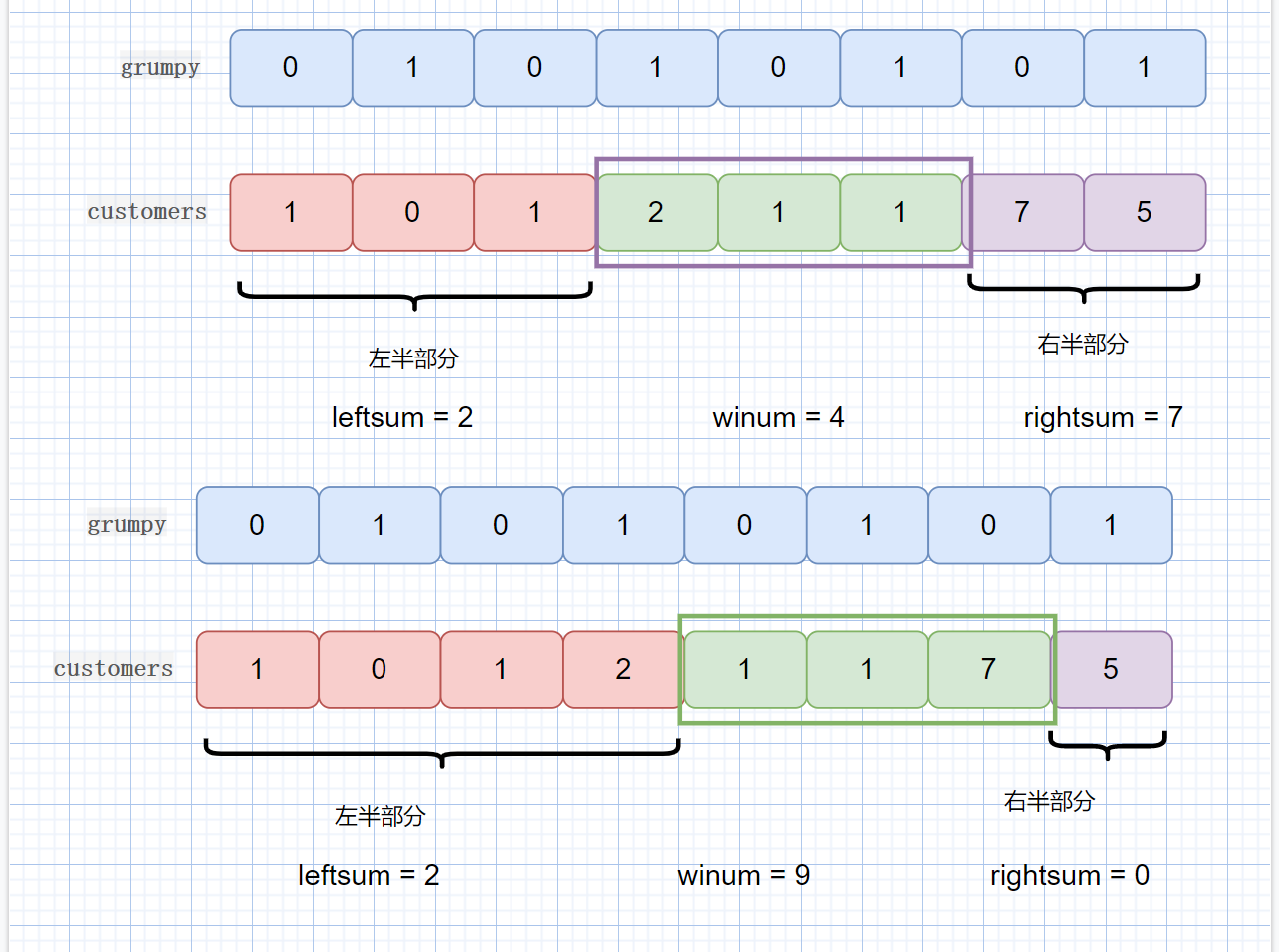
|
||
|
||
我们此时移动了窗口,
|
||
|
||
则左半区间范围扩大,但是 leftsum 的值没有变,这时因为新加入的值,所对应的 grumpy[i] == 1,所以其值不会发生改变,因为我们只统计 grumpy[i] == 0 的值,
|
||
|
||
右半区间范围减少,rightsum 值也减少,因为右半区间减小的值,其对应的 grumpy[i] == 0,所以 rightsum -= grumpy[i]。
|
||
|
||
winsum 也会发生变化, winsum 需要加上新加入窗口的值,减去刚离开窗口的值, 也就是 customer[left-1],left 代表窗口左边缘。
|
||
|
||
好啦,知道怎么做了,我们直接开整吧。
|
||
|
||
```java
|
||
class Solution {
|
||
public int maxSatisfied(int[] customers, int[] grumpy, int X) {
|
||
|
||
int winsum = 0;
|
||
int rightsum = 0;
|
||
int len = customers.length;
|
||
//右区间的值
|
||
for (int i = X; i < len; ++i) {
|
||
if (grumpy[i] == 0) {
|
||
rightsum += customers[i];
|
||
}
|
||
}
|
||
//窗口的值
|
||
for (int i = 0; i < X; ++i) {
|
||
winsum += customers[i];
|
||
}
|
||
int leftsum = 0;
|
||
//窗口左边缘
|
||
int left = 1;
|
||
//窗口右边缘
|
||
int right = X;
|
||
int maxcustomer = winsum + leftsum + rightsum;
|
||
while (right < customers.length) {
|
||
//重新计算左区间的值,也可以用 customer 值和 grumpy 值相乘获得
|
||
if (grumpy[left-1] == 0) {
|
||
leftsum += customers[left-1];
|
||
}
|
||
//重新计算右区间值
|
||
if (grumpy[right] == 0) {
|
||
rightsum -= customers[right];
|
||
}
|
||
//窗口值
|
||
winsum = winsum - customers[left-1] + customers[right];
|
||
//保留最大值
|
||
maxcustomer = Math.max(maxcustomer,winsum+leftsum+rightsum);
|
||
//移动窗口
|
||
left++;
|
||
right++;
|
||
}
|
||
return maxcustomer;
|
||
}
|
||
}
|
||
```
|
||
|
||
|