mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-20 02:53:39 +00:00
90 lines
3.1 KiB
Markdown
90 lines
3.1 KiB
Markdown
### leetcode1248. 统计「优美子数组」
|
||
|
||
**题目描述**
|
||
|
||
> 给你一个整数数组 nums 和一个整数 k。
|
||
>
|
||
> 如果某个 连续 子数组中恰好有 k 个奇数数字,我们就认为这个子数组是「优美子数组」。
|
||
>
|
||
> 请返回这个数组中「优美子数组」的数目。
|
||
|
||
**示例 1:**
|
||
|
||
> 输入:nums = [1,1,2,1,1], k = 3
|
||
> 输出:2
|
||
> 解释:包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。
|
||
|
||
**示例 2:**
|
||
|
||
> 输入:nums = [2,4,6], k = 1
|
||
> 输出:0
|
||
> 解释:数列中不包含任何奇数,所以不存在优美子数组。
|
||
|
||
**示例 3:**
|
||
|
||
> 输入:nums = [2,2,2,1,2,2,1,2,2,2], k = 2
|
||
> 输出:16
|
||
|
||
如果上面那个题目我们完成了,这个题目做起来,分分钟的事,不信你去写一哈,百分百就整出来了,我们继续按上面的思想来解决。
|
||
|
||
**HashMap**
|
||
|
||
**解析**
|
||
|
||
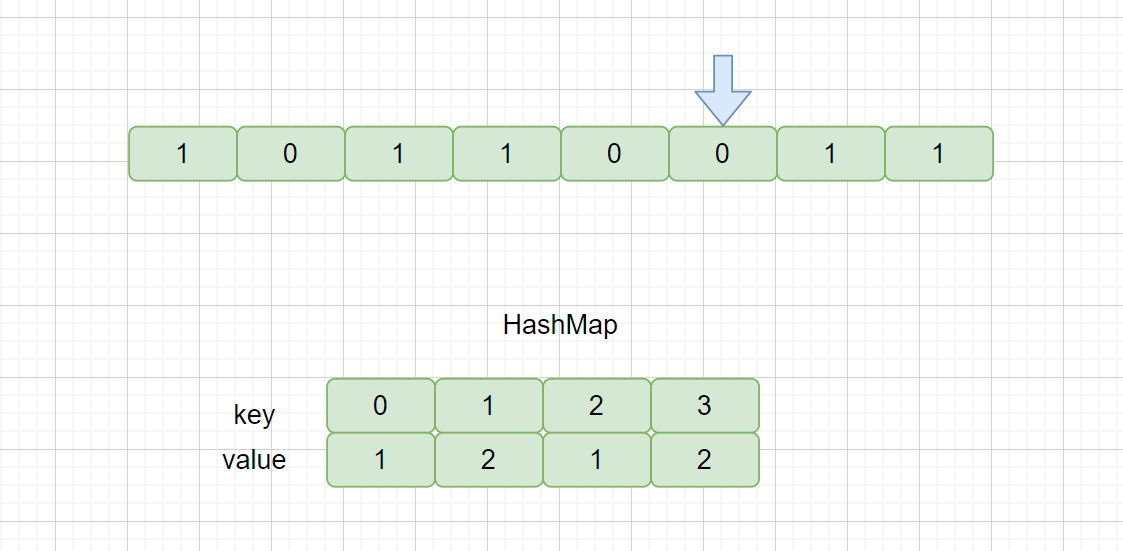
上个题目我们是求和为 K 的子数组,这个题目是让我们求 恰好有 k 个奇数数字的连续子数组,这两个题几乎是一样的,上个题中我们将前缀区间的和保存到哈希表中,这个题目我们只需将前缀区间的奇数个数保存到区间内即可,只不过将 sum += x 改成了判断奇偶的语句,见下图。
|
||
|
||
|
||
|
||
我们来解析一下哈希表,key 代表的是含有 1 个奇数的前缀区间,value 代表这种子区间的个数,含有两个,也就是nums[0],nums[0,1].后面含义相同,那我们下面直接看代码吧,一下就能读懂。
|
||
|
||
```java
|
||
class Solution {
|
||
public int numberOfSubarrays(int[] nums, int k) {
|
||
|
||
if (nums.length == 0) {
|
||
return 0;
|
||
}
|
||
HashMap<Integer,Integer> map = new HashMap<>();
|
||
//统计奇数个数,相当于我们的 presum
|
||
int oddnum = 0;
|
||
int count = 0;
|
||
map.put(0,1);
|
||
for (int x : nums) {
|
||
// 统计奇数个数
|
||
oddnum += x & 1;
|
||
// 发现存在,则 count增加
|
||
if (map.containsKey(oddnum - k)) {
|
||
count += map.get(oddnum - k);
|
||
}
|
||
//存入
|
||
map.put(oddnum,map.getOrDefault(oddnum,0)+1);
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
但是也有一点不同,就是我们是统计奇数的个数,数组中的奇数个数肯定不会超过原数组的长度,所以这个题目中我们可以用数组来模拟 HashMap ,用数组的索引来模拟 HashMap 的 key,用值来模拟哈希表的 value。下面我们直接看代码吧。
|
||
|
||
```java
|
||
class Solution {
|
||
public int numberOfSubarrays(int[] nums, int k) {
|
||
int len = nums.length;
|
||
int[] map = new int[len + 1];
|
||
map[0] = 1;
|
||
int oddnum = 0;
|
||
int count = 0;
|
||
for (int i = 0; i < len; ++i) {
|
||
//如果是奇数则加一,偶数加0,相当于没加
|
||
oddnum += nums[i] & 1;
|
||
if (oddnum - k >= 0) {
|
||
count += map[oddnum-k];
|
||
}
|
||
map[oddnum]++;
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
### |