mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-19 18:43:38 +00:00
107 lines
5.8 KiB
Markdown
107 lines
5.8 KiB
Markdown
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||
>
|
||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||
>
|
||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||
|
||
### **希尔排序 (Shell's Sort)**
|
||
|
||
我们在之前说过直接插入排序在记录基本有序的时候和元素较少时效率是很高的,基本有序时,只需执行少量的插入操作,就可以完成整个记录的排序工作。当元素较少时,效率也很高,就比如我们经常用的 Arrays.sort (),当元素个数少于47时,使用的排序算法就是直接插入排序。那么直接希尔排序和直接插入排序有什么关系呢?
|
||
|
||
希尔排序是**插入排序**的一种,又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序的高级变形,其思想简单点说就是有跨度的插入排序,这个跨度会逐渐变小,直到变为 1,变为 1 时记录也就基本有序,这时用到的也就是我们之前讲的直接插入排序了。
|
||
|
||
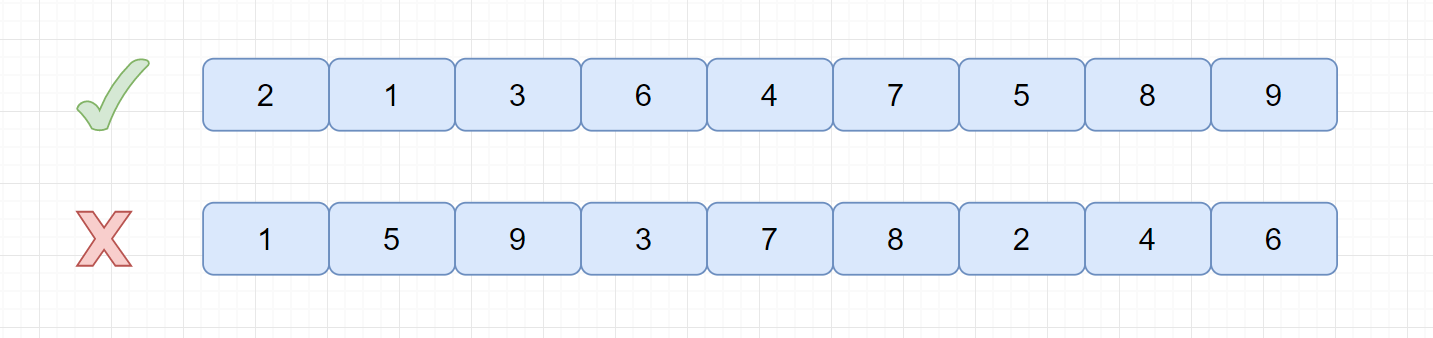
基本有序:就是小的关键字基本在前面,大的关键字基本在后面,不大不小的基本在中间。见下图。
|
||
|
||
|
||
|
||
我们已经了解了希尔排序的基本思想,下面我们通过一个绘图来描述下其执行步骤。
|
||
|
||

|
||
|
||
先逐步分组进行粗调,在进行直接插入排序的思想就是希尔排序。我们刚才的分组跨度(4,2,1)被称为希尔排序的增量,我们上面用到的是逐步折半的增量方法,这也是在发明希尔排序时提出的一种朴素方法,被称为希尔增量,
|
||
|
||
下面我们用动图模拟下使用希尔增量的希尔排序的执行过程
|
||
|
||

|
||
|
||
大家可能看了视频模拟,也不是特别容易写出算法代码,不过你们看到代码肯定会很熟悉滴。
|
||
|
||
**希尔排序代码**
|
||
|
||
```java
|
||
class Solution {
|
||
public int[] sortArray(int[] nums) {
|
||
int increment = nums.length;
|
||
//注意看结束条件
|
||
while (increment > 1) {
|
||
//这里可以自己设置
|
||
increment = increment / 2;
|
||
//根据增量分组
|
||
for (int i = 0; i < increment; ++i) {
|
||
//这快是不是有点面熟,回去看看咱们的插入排序
|
||
for (int j = i + increment; j < nums.length; ++j) {
|
||
int temp = nums[j];
|
||
int k;
|
||
for (k = j - increment; k >= 0; k -= increment) {
|
||
if (temp < nums[k]) {
|
||
nums[k+increment] = nums[k];
|
||
continue;
|
||
}
|
||
break;
|
||
}
|
||
nums[k+increment] = temp;
|
||
}
|
||
}
|
||
}
|
||
return nums;
|
||
}
|
||
}
|
||
```
|
||
|
||
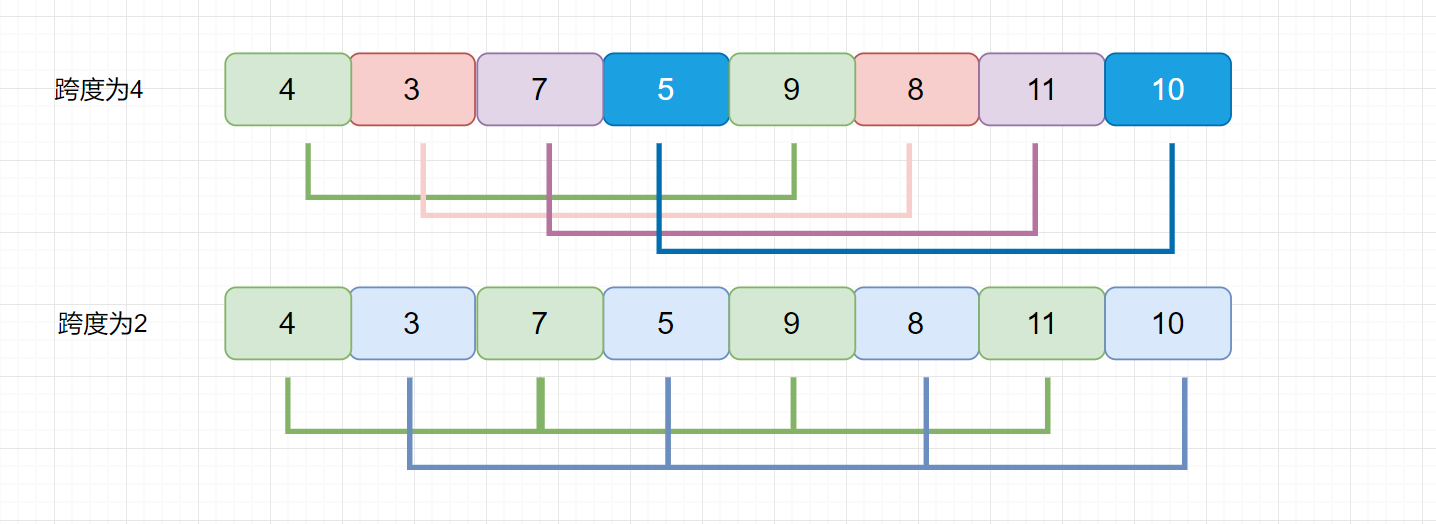
我们刚才说,我们的增量可以自己设置的,我们上面的例子是用的希尔增量,下面我们看这个例子,看看使用希尔增量会出现什么问题。
|
||
|
||
|
||
|
||
我们发现无论是以 4 为增量,还是以 2 为增量,每组内部的元素没有任何交换。直到增量为 1 时,数组才会按照直接插入排序进行调整。所以这种情况希尔排序的效率是低于直接插入排序呢?
|
||
|
||
我们的希尔增量因为每一轮之间是等比的,所以会有盲区,这里增量的选取就非常关键了。
|
||
|
||
下面给大家介绍两个比较有代表性的 Sedgewick 增量和 Hibbard 增量
|
||
|
||
Sedgewick 增量序列如下:
|
||
|
||
1,5,19,41,109.。。。
|
||
|
||
通项公式 9*4^k - 9*2^
|
||
|
||
利用此种增量方式的希尔排序,最坏时间复杂度是O(n^(4/3))
|
||
|
||
Hibbard增量序列如下:
|
||
|
||
1,3,7,15......
|
||
|
||
通项公式2 ^ k-1
|
||
|
||
利用此种增量方式的希尔排序,最坏时间复杂度为O(n^(3/2))
|
||
|
||
上面是两种比较具有代表性的增量方式,可究竟应该选取怎样的增量才是最好,目前还是一个数学难题。不过我们需要注意的一点,就是增量序列的最后一个增量值必须等于1才行。
|
||
|
||
**希尔排序时间复杂度分析**
|
||
|
||
希尔排序的时间复杂度跟增量序列的选择有关,范围为 O(n^(1.3-2)) 在此之前的排序算法时间复杂度基本都是O(n^2),希尔排序是突破这个时间复杂度的第一批算法之一。
|
||
|
||
**希尔排序空间复杂度分析**
|
||
|
||
根据我们的视频可知希尔排序的空间复杂度为 O(1),
|
||
|
||
**希尔排序的稳定性分析**
|
||
|
||
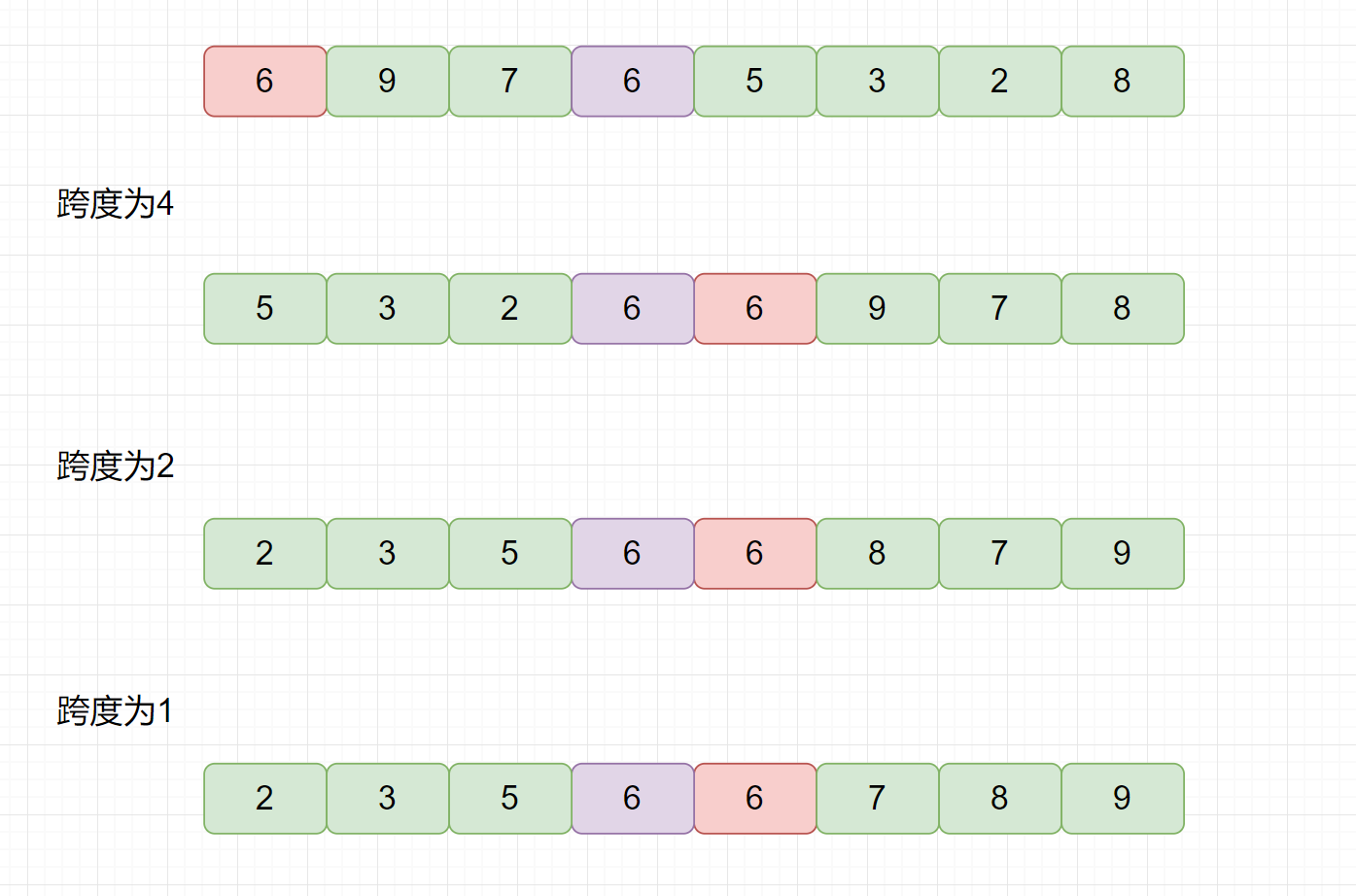
我们见下图,一起来分析下希尔排序的稳定性。
|
||
|
||
|
||
|
||
通过上图,可知,如果我们选用 4 为跨度的话,交换后,两个相同元素 2 的相对位置会发生改变,所以希尔排序是一个不稳定的排序
|
||
|
||

|
||
|