algorithm-base/animation-simulation/求和问题/四数之和.md

四数之和

题目描述

给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。

注意：

答案中不可以包含重复的四元组。

示例：

给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。

满足要求的四元组集合为： [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]

我们已经完成了两数之和和三数之和，这个题目应该就手到擒来了，因为我们已经知道这类题目的解题框架，两数之和呢，我们就先固定第一个数 ，然后移动指针去找第二个符合的，三数之和，固定一个数，双指针去找符合情况的其他两位数，那么我们四数之和，也可以先固定两个数，然后利用双指针去找另外两位数。所以我们来搞定他吧。

多指针：

解析：

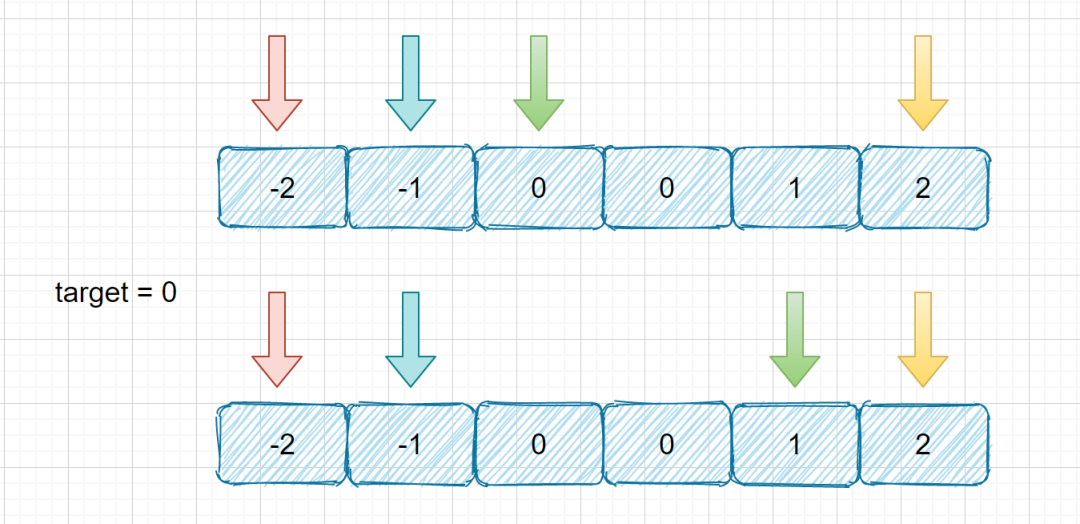
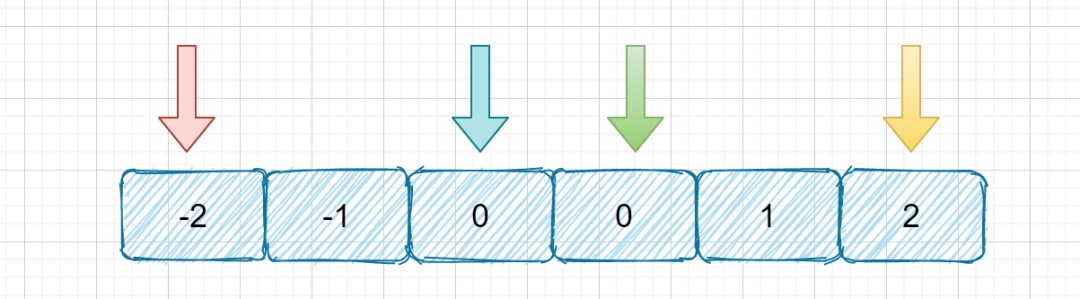
三数之和是，我们首先确定一个数，然后利用双指针去找另外的两个数，我们在这个题目里面的解题思路是需要首先确定两个数然后利用双指针去找另外两个数，和三数之和思路基本一致很容易理解。我们具体思路可以参考下图。

这里需要注意的是，我们的 target 不再和三数之和一样为 0 ，target 是不固定的，所以解题思路不可以完全照搬上面的题目。另外这里也需要考虑去重的情况，思路和上题一致。

上图则为我们查找到一个符合条件的四元组的情况，查找成功之后，下一步移动蓝色指针，重新定义绿蓝指针，继续执行上面步骤。

动图解析：

题目代码：

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
           if(nums.length < 4){
               return new ArrayList<>(); 
           }
           Arrays.sort(nums);
           List<List<Integer>> arr = new ArrayList<>();
           for (int i = 0; i < nums.length-3; ++i) {
               if (i > 0 && nums[i] == nums[i-1]) {
                   continue;
               }
               for (int j = i+1; j < nums.length-2; j++) {

                   if (j > i+1 && nums[j] == nums[j-1]) {
                       continue;
                   }
                   int l = j+1;
                   int r = nums.length-1;
                   while (l < r) {
                       int sum = nums[i] + nums[j] + nums[l] + nums[r];
                       if (sum == target) {
                           //存入
                           arr.add(new ArrayList<>
                           (Arrays.asList(nums[i], nums[j], nums[l], nums[r])));
                           //去重
                           while (l < r && nums[l] == nums[l+1]) {
                               l++;
                           }
                           while (l < r && nums[r] == nums[r-1]) {
                               r--;
                           }
                           l++;
                           r--;
                       }
                       else if (sum > target) {
                             r--;
                       }
                       else {
                             l++;
                       }
                   }
               }
           }
           return arr;
    }
}