7.7 KiB
如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 tan45du_one ,备注 github + 题目 + 问题 向我反馈
感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
另外希望手机阅读的同学可以来我的 公众号:袁厨的算法小屋 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击刷题小队进入。
15. 三数之和
题目描述:
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
这个题目算是对刚才题目的升级,刚才题目我们是只需返回一个例子即可,但是这个题目是让我们返回所有情况,这个题目我们需要返回三个数相加为 0 的所有情况,但是我们需要去掉重复的三元组(算是该题的核心),所以这个题目还是挺有趣的,大家记得打卡呀。
哈希表:
解析
我们这个题目的哈希表解法是很容易理解的,我们首先将数组排序,排序之后我们将排序过的元素存入哈希表中,我们首先通过两层遍历,确定好前两位数字,那么我们只需要哈希表是否存在符合情况的第三位数字即可,跟暴力解法的思路类似,很容易理解,
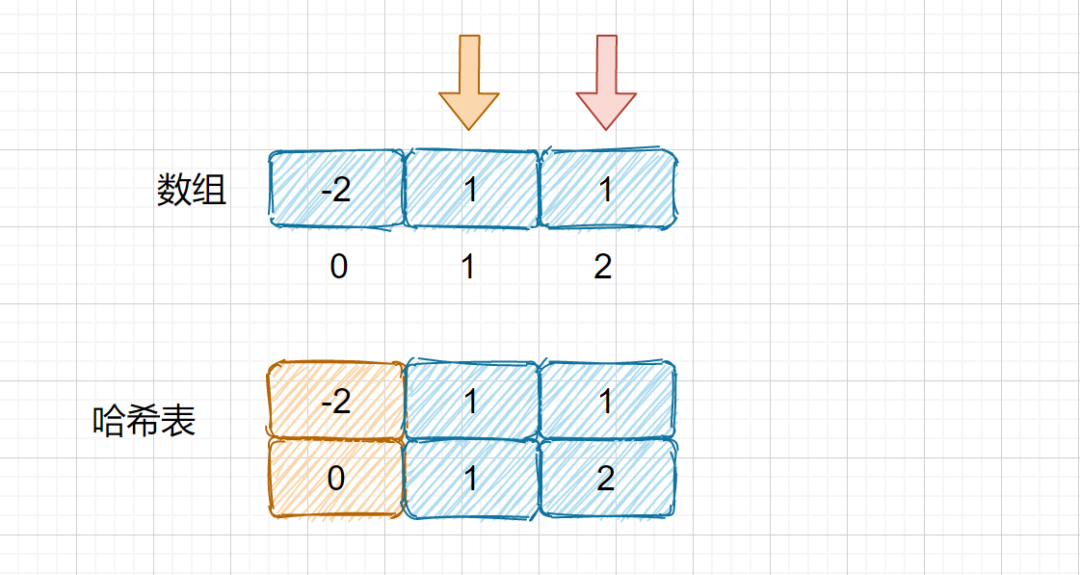
但是这里我们需要注意的情况就是,例如我们的例子为[-2 , 1 , 1],如果我们完全按照以上思路来的话,则会出现两个解,[-2 , 1 , 1]和[1 , 1, -2]。具体原因,确定 -2,1之后发现 1 在哈希表中,存入。确定 1 ,1 之后发现 -2 在哈希表中,存入。
所以我们需要加入一个约束避免这种情况,那就是我们第三个数的索引大于第二个数时才存入。
上面这种情况时是不可以存入的,因为我们虽然在哈希表中找到了符合要求的值,但是 -2 的索引为 0 小于 2 所以不可以存入。
题目代码
class Solution {
public List<List<Integer>> threeSum (int[] nums) {
if (nums.length < 3) {
return new ArrayList<>();
}
//排序
Arrays.sort(nums);
HashMap<Integer,Integer> map = new HashMap<>();
List<List<Integer>> resultarr = new ArrayList<>();
//存入哈希表
for (int i = 0; i < nums.length; i++) {
map.put(nums[i],i);
}
Integer t;
int target = 0;
for (int i = 0; i < nums.length; ++i) {
target = -nums[i];
//去重
if (i > 0 && nums[i] == nums[i-1]) {
continue;
}
for (int j = i + 1; j < nums.length; ++j) {
if (j > i+1 && nums[j] == nums[j-1]) {
continue;
}
if ((t = map.get(target - nums[j])) != null) {
//符合要求的情况,存入
if (t > j) {
resultarr.add(new ArrayList<>
(Arrays.asList(nums[i], nums[j], nums[t])));
}
else {
break;
}
}
}
}
return resultarr;
}
}
多指针
解析:
如果我们将上个题目得指针解法称做是双指针的话,那么这个题目用到的方法就是三指针,因为我们是三数之和嘛,一个指针对应一个数,下面我们看一下具体思路,其实原理很简单,我们先将数组排序,直接 Arrays.sort() 解决,排序之后处理起来就很容易了。
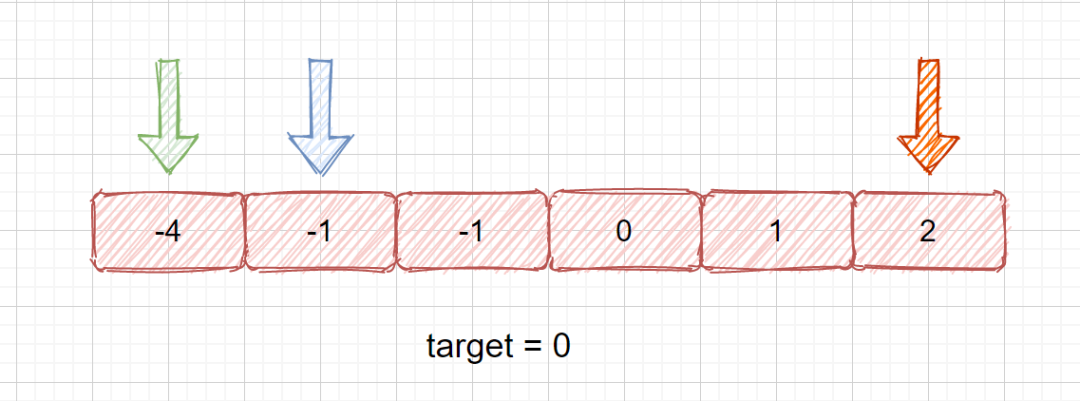
下面我们来看下三个指针的初始位置。
初始情况见上图,我们看当前情况,三数之和为 -3 ,很显然不是 0 ,那么我们应该怎么做呢?
我们设想一下,我们当前的三数之和为 -3 < 0 那么我们如果移动橙色指针的话则会让我们的三数之和变的更小,因为我们的数组是有序的,所以我们移动橙色指针(蓝色不动)时和会变小,如果移动蓝色指针(橙色不动)的话,三数之和则会变大,所以这种情况则需要向右移动我们的蓝色指针,
找到三数之和等于 0 的情况进行保存,如果三数之和大于 0 的话,则需要移动橙色指针,途中有三数之和为 0 的情况则保存。直至蓝橙两指针相遇跳出该次循环,然后我们的绿指针右移一步,继续执行上诉步骤。
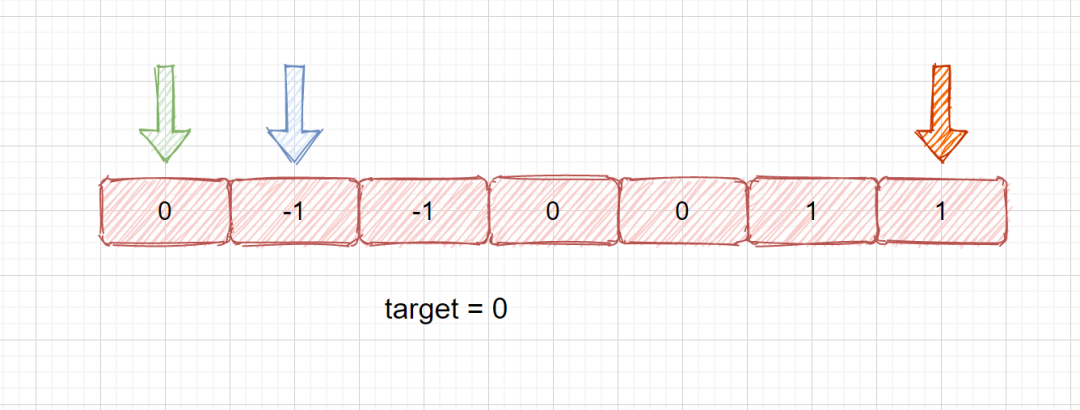
但是这里我们需要注意的一个细节就是,我们需要去除相同三元组的情况,我们看下面的例子。
这里我们发现 0 - 1 + 1 = 0,当前情况是符合的,所以我们需要存入该三元组,存入后,蓝色指针向后移动一步,橙色指针向前移动一步,我们发现仍为 0 -1 + 1 = 0 仍然符合,但是如果继续存入该三元组的话则不符合题意,所以我们需要去重。
这里可以借助HashSet但是效率太差,不推荐。
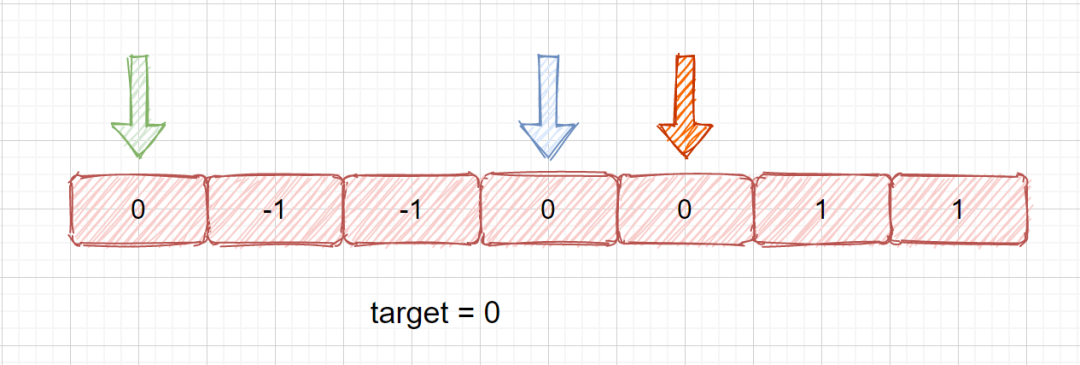
这里我们可以使用 while 循环将蓝色指针移动到不和刚才相同的位置,也就是直接移动到元素 0 上,橙色指针同样也是。则是下面这种情况,
这样我们就实现了去重,然后继续判断当前三数之和是否为 0 。
动图解析:
题目代码:
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> arr = new ArrayList<List<Integer>>();
if(nums.length < 3){
return arr;
}
//排序
Arrays.sort(nums);
if(nums[0] > 0){
return arr;
}
for(int i = 0; i < nums.length-2; i++){
int target = 0 - nums[i];
//去重
if(i > 0 && nums[i] == nums[i-1]){
continue;
}
int l = i+1;
int r = nums.length - 1;
while(l < r){
if(nums[l] + nums[r] == target){
//存入符合要求的值
arr.add(new ArrayList<>(Arrays.asList(nums[i], nums[l], nums[r])));
//这里需要注意顺序
while(l < r && nums[l] == nums[l+1]) l++;
while(l < r && nums[r] == nums[r-1]) r--;
l++;
r--;
}
else if(nums[l] + nums[r] > target){
r--;
}
else{
l++;
}
}
}
return arr;
}
}