8.3 KiB
如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 tan45du_one ,备注 github + 题目 + 问题 向我反馈
感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
另外希望手机阅读的同学可以来我的 公众号:袁厨的算法小屋 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击刷题小队进入。
什么是二分?
废话不多说,让导演帮我们把镜头切到袁记菜馆吧!
袁记菜馆内。。。。
店小二:掌柜的,您进货回来了呀,哟!今天您买这鱼挺大呀!
袁厨:那是,这是我今天从咱们江边买的,之前一直去菜市场买,那里的老贵了,你猜猜我今天买的多少钱一条。
店小二:之前的鱼,30 个铜板一条,今天的我猜 26 个铜板。
袁厨:贵了。
店小二:还贵呀!那我猜 20 个铜板!
袁厨:还是贵了。
店小二:15 个铜板。
袁厨:便宜了
店小二:18 个铜板
袁厨:恭喜你猜对了
上面的例子就用到了我们的二分查找思想,如果你玩过类似的游戏,那二分查找理解起来肯定很轻松啦,下面我们一起征服二分查找吧!
完全有序
二分查找
二分查找也称折半查找(Binary Search),是一种在有序数组中查找某一特定元素的搜索算法。我们可以从定义可知,运用二分搜索的前提是数组必须是有序的,这里需要注意的是,我们的输入不一定是数组,也可以是数组中某一区间的起始位置和终止位置
通过上面二分查找的定义,我们知道了二分查找算法的作用及要求,那么该算法的具体执行过程是怎样的呢?
下面我们通过一个例子来帮助我们理解。我们需要在 nums 数组中,查询元素 8 的索引
int[ ] nums = {1,3,4,5,6,8,12,14,16}; target = 8
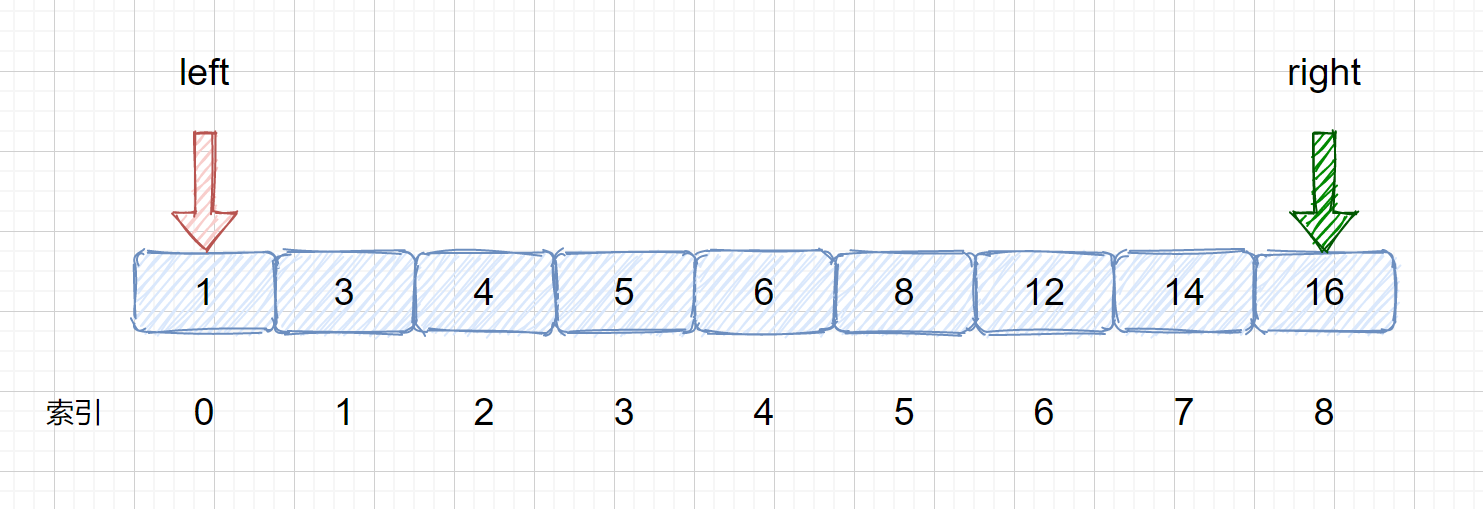
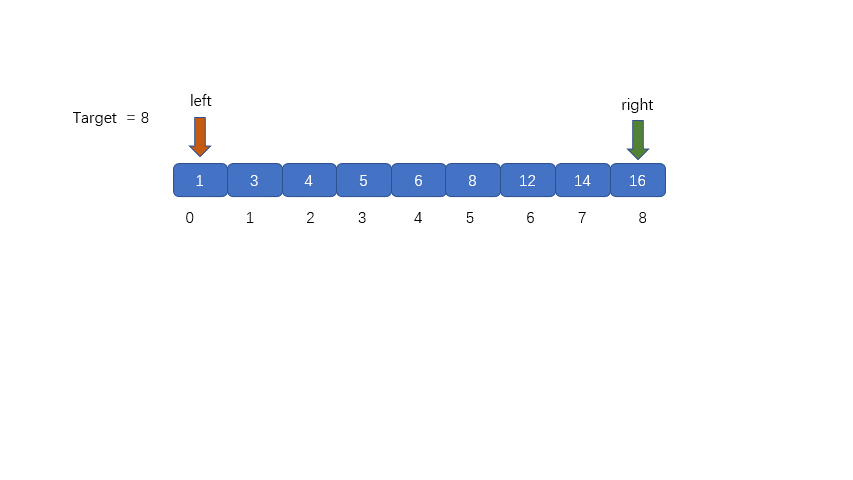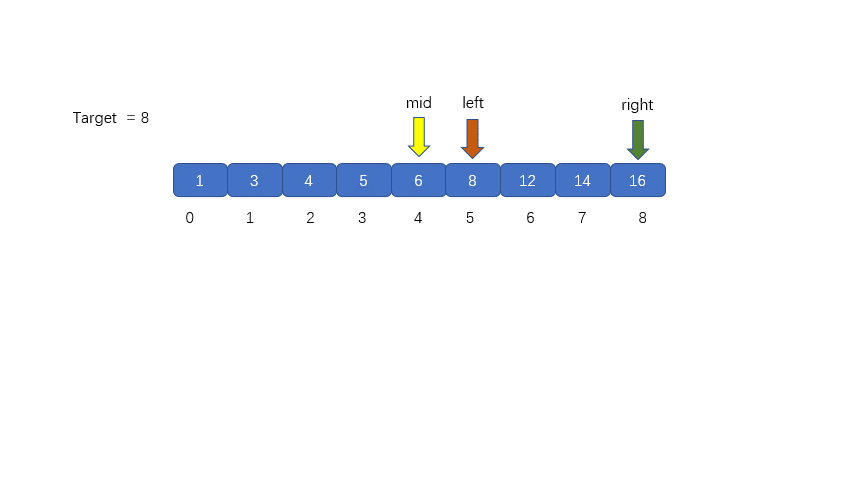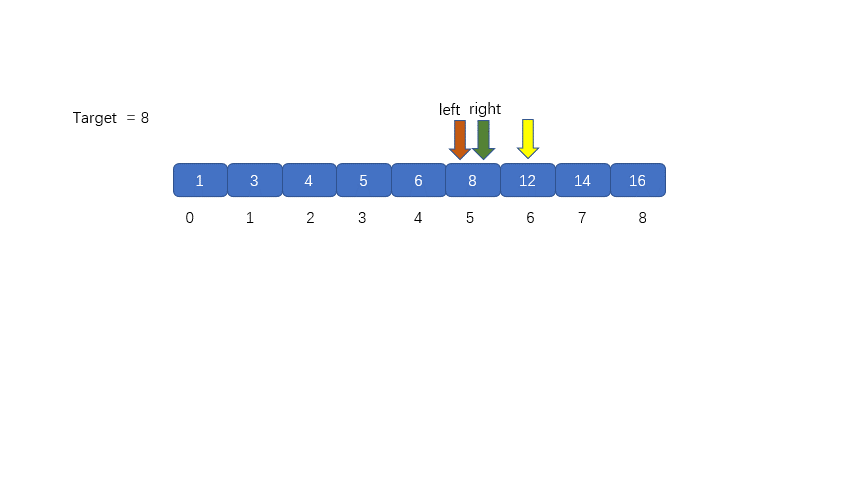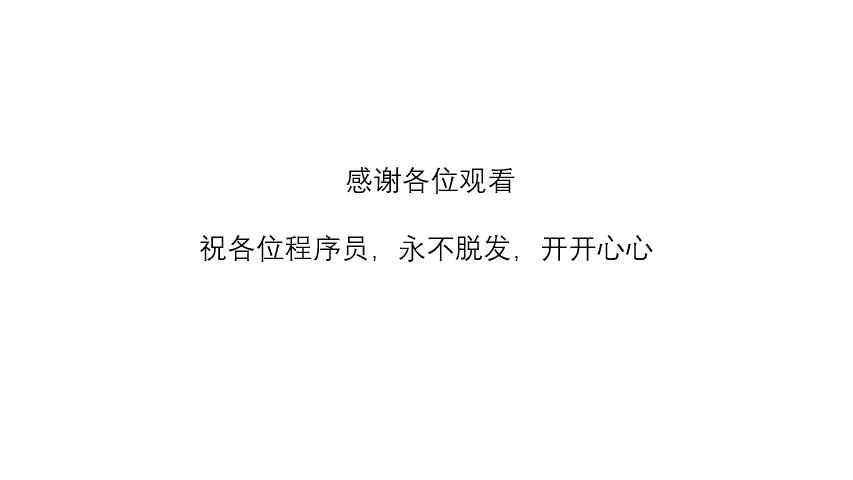
(1)我们需要定义两个指针分别指向数组的头部及尾部,这是我们在整个数组中查询的情况,当我们在数组
某一区间进行查询时,可以输入数组,起始位置,终止位置进行查询。
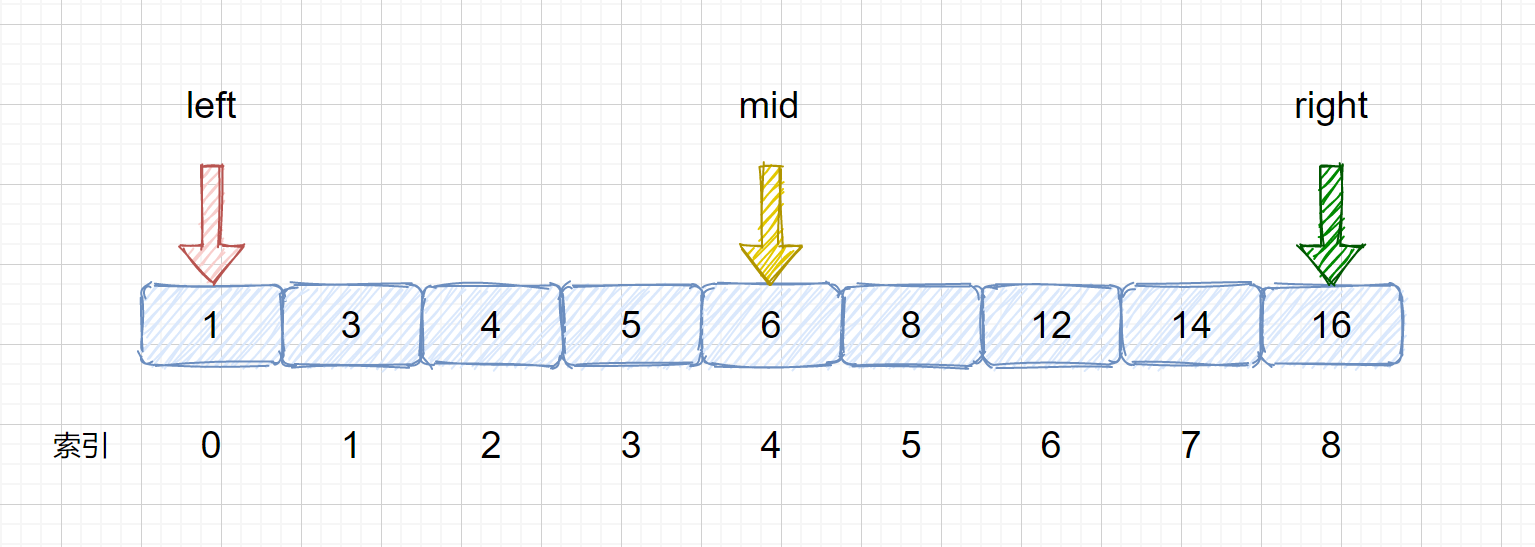
(2)找出 mid,该索引为 mid =(left + right)/ 2,但是这样写有可能溢出,所以我们需要改进一下写成
mid = left +(right - left)/ 2 或者 left + ((right - left ) >> 1) 两者作用是一样的,都是为了找到两指针的中
间索引,使用位运算的速度更快。那么此时的 mid = 0 + (8-0) / 2 = 4
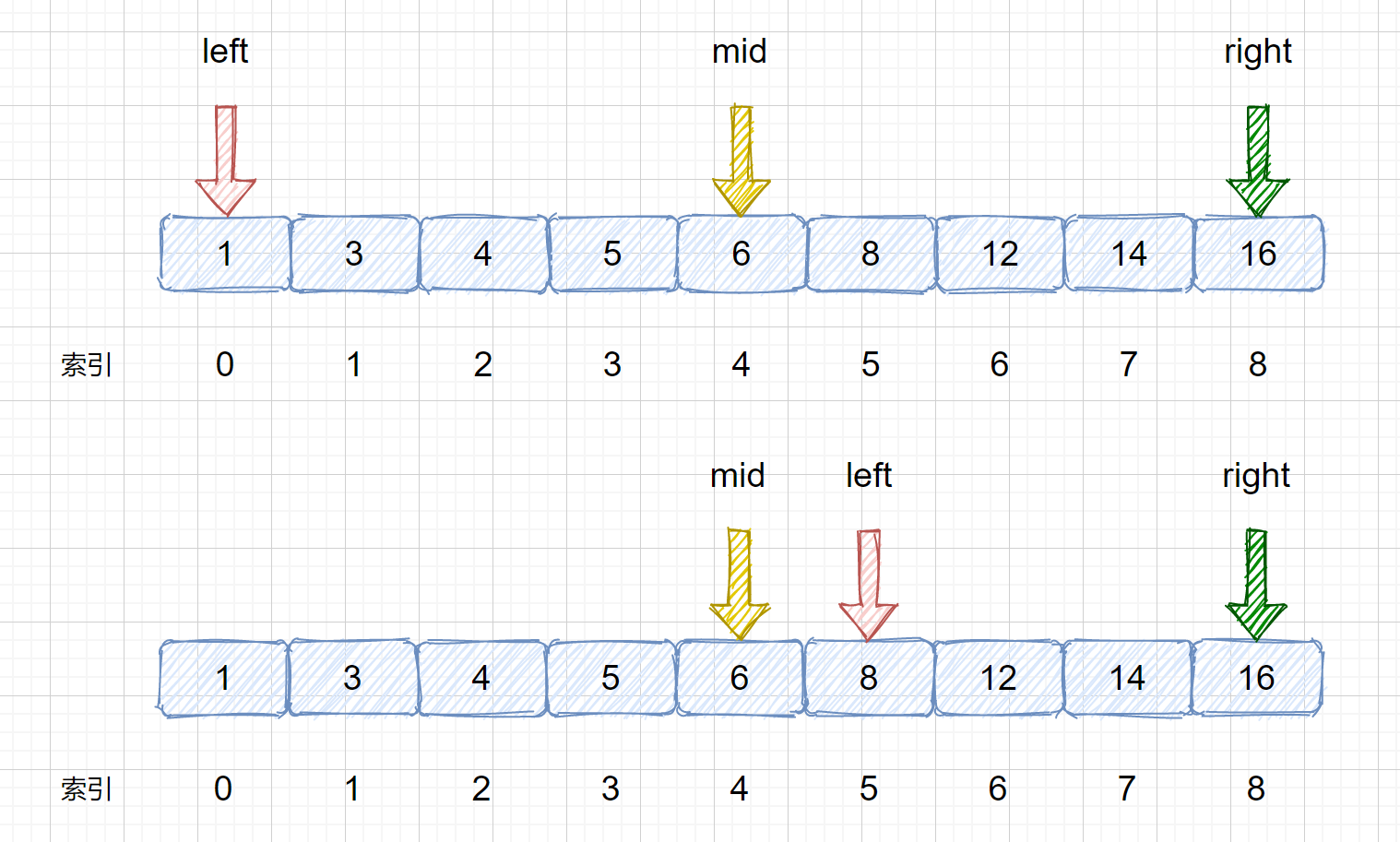
(3)此时我们的 mid = 4,nums[mid] = 6 < target,那么我们需要移动我们的 left 指针,让 left = mid + 1,下次则可以在新的 left 和 right 区间内搜索目标值,下图为移动前和移动后
(4)我们需要在 left 和 right 之间计算 mid 值,mid = 5 + (8 - 5)/ 2 = 6 然后将 nums[mid] 与 target 继续比较,进而决定下次移动 left 指针还是 right 指针,见下图
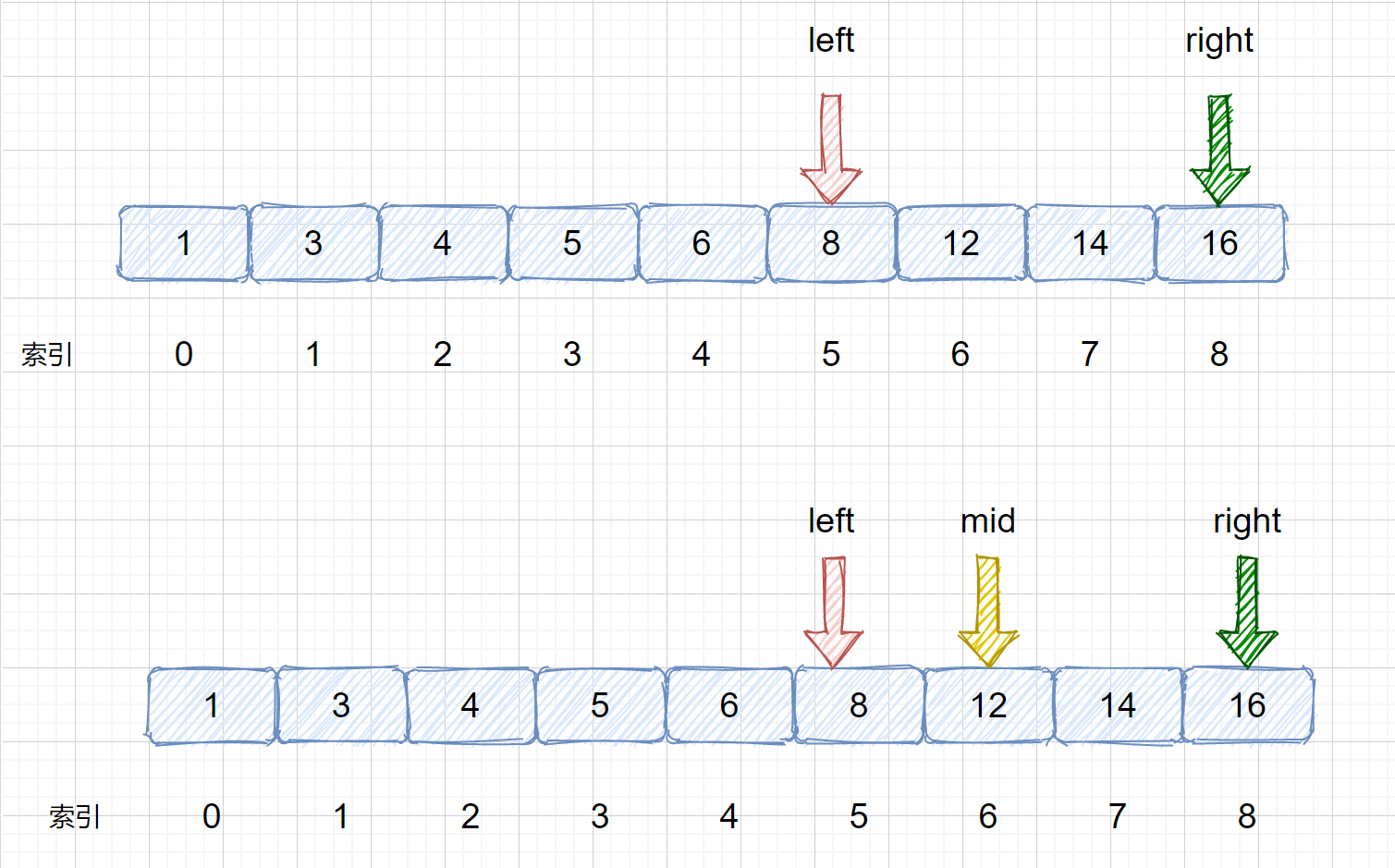
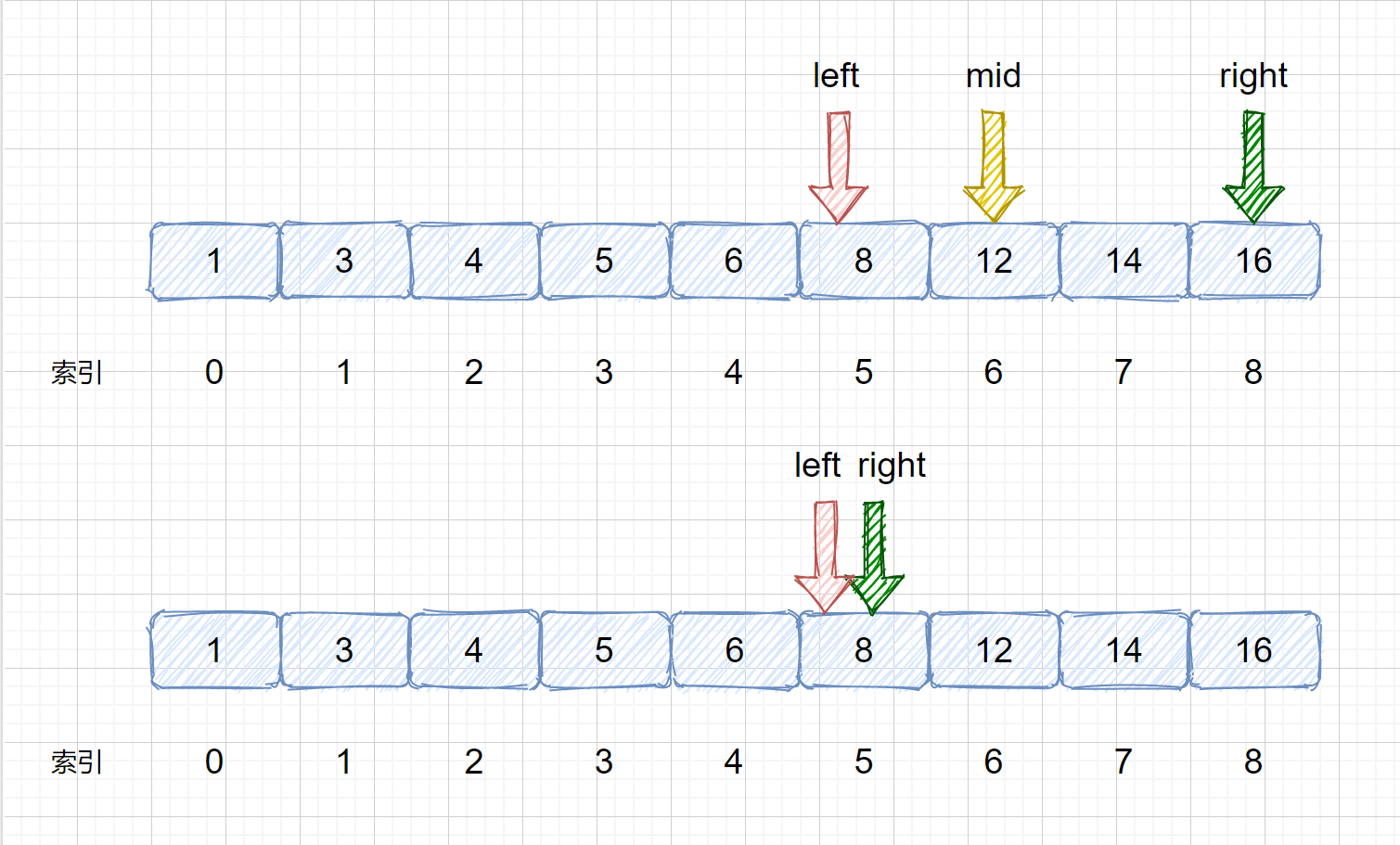
(5)我们发现 nums[mid] > target,则需要移动我们的 right 指针, 则 right = mid - 1;则移动过后我们的 left 和 right 会重合,这里是我们的一个重点大家需要注意一下,后面会对此做详细叙述。
(6)我们需要在 left 和 right 之间继续计算 mid 值,则 mid = 5 +(5 - 5)/ 2 = 5 ,见下图,此时我们将 nums[mid] 和 target 比较,则发现两值相等,返回 mid 即可 ,如果不相等则跳出循环,返回 -1。
二分查找的执行过程如下
1.从已经排好序的数组或区间中,取出中间位置的元素,将其与我们的目标值进行比较,判断是否相等,如果相等
则返回。
2.如果 nums[mid] 和 target 不相等,则对 nums[mid] 和 target 值进行比较大小,通过比较结果决定是从 mid
的左半部分还是右半部分继续搜索。如果 target > nums[mid] 则右半区间继续进行搜索,即 left = mid + 1; 若
target < nums[mid] 则在左半区间继续进行搜索,即 right = mid -1;
动图解析
下面我们来看一下二分查找的代码,可以认真思考一下 if 语句的条件,每个都没有简写。
Java Code:
public static int binarySearch(int[] nums,int target,int left, int right) {
//这里需要注意,循环条件
while (left <= right) {
//这里需要注意,计算mid
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}else if (nums[mid] < target) {
//这里需要注意,移动左指针
left = mid + 1;
}else if (nums[mid] > target) {
//这里需要注意,移动右指针
right = mid - 1;
}
}
//没有找到该元素,返回 -1
return -1;
}
Go Code:
func binarySearch(nums []int, target, left, right int) int {
//这里需要注意,循环条件
for left <= right {
//这里需要注意,计算mid
mid := left + ((right - left) >> 1)
if nums[mid] == target {
return mid
} else if nums[mid] < target {
//这里需要注意,移动左指针
left = mid + 1
} else if nums[mid] > target {
//这里需要注意,移动右指针
right = mid - 1
}
}
//没有找到该元素,返回 -1
return -1
}
二分查找的思路及代码已经理解了,那么我们来看一下实现时容易出错的地方
1.计算 mid 时 ,不能使用 (left + right )/ 2,否则有可能会导致溢出
2.while (left < = right) { } 注意括号内为 left <= right ,而不是 left < right ,我们继续回顾刚才的例子,如果我们设置条件为 left < right 则当我们执行到最后一步时,则我们的 left 和 right 重叠时,则会跳出循环,返回 -1,区间内不存在该元素,但是不是这样的,我们的 left 和 right 此时指向的就是我们的目标元素 ,但是此时 left = right 跳出循环
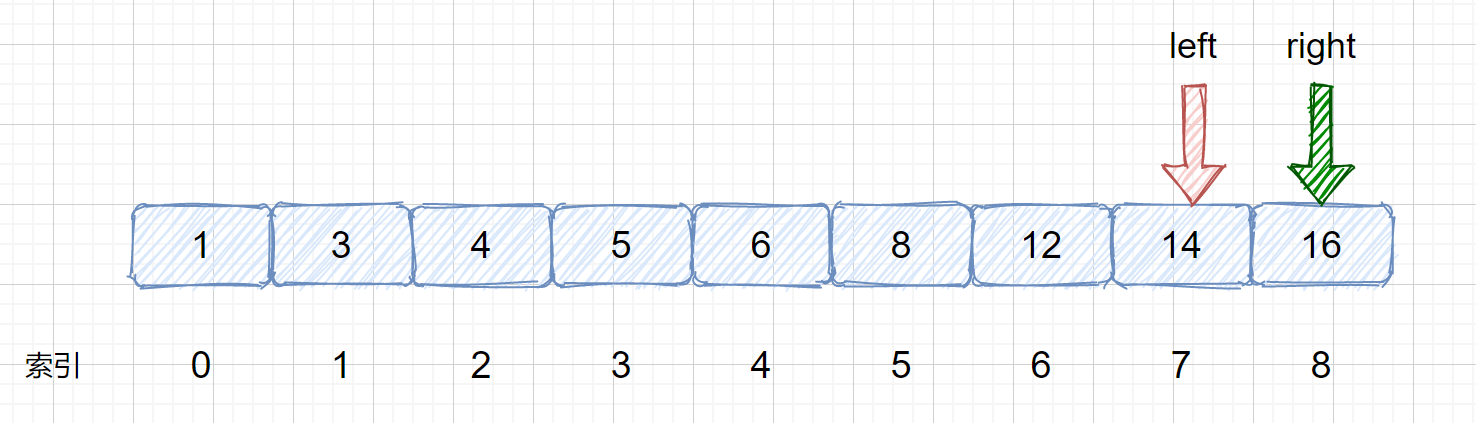
- left = mid + 1,right = mid - 1 而不是 left = mid 和 right = mid。我们思考一下这种情况,见下图,当我们的 target 元素为 16 时,然后我们此时 left = 7 ,right = 8,mid = left + (right - left) = 7 + (8-7) = 7,那如果设置 left = mid 的话,则会进入死循环,mid 值一直为 7 。
下面我们来看一下二分查找的递归写法
Java Code:
public static int binarySearch(int[] nums,int target,int left, int right) {
if (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
//查找成功
return mid;
}else if (nums[mid] > target) {
//新的区间,左半区间
return binarySearch(nums,target,left,mid-1);
}else if (nums[mid] < target) {
//新的区间,右半区间
return binarySearch(nums,target,mid+1,right);
}
}
//不存在返回-1
return -1;
}
Go Code:
func binarySearch(nums []int, target, left, right int) int {
if left <= right {
mid := left + ((right - left) >> 1)
if nums[mid] == target {
//查找成功
return mid
} else if nums[mid] > target {
//新的区间,左半区间
return binarySearch(nums, target, left, mid-1)
} else if nums[mid] < target {
//新的区间,右半区间
return binarySearch(nums, target, mid+1, right)
}
}
//不存在返回-1
return -1
}