mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-14 16:13:39 +00:00
3.5 KiB
3.5 KiB
我们之前说了二叉树基础及二叉的几种遍历方式及练习题,今天我们来看一下二叉树的前序遍历非递归实现。
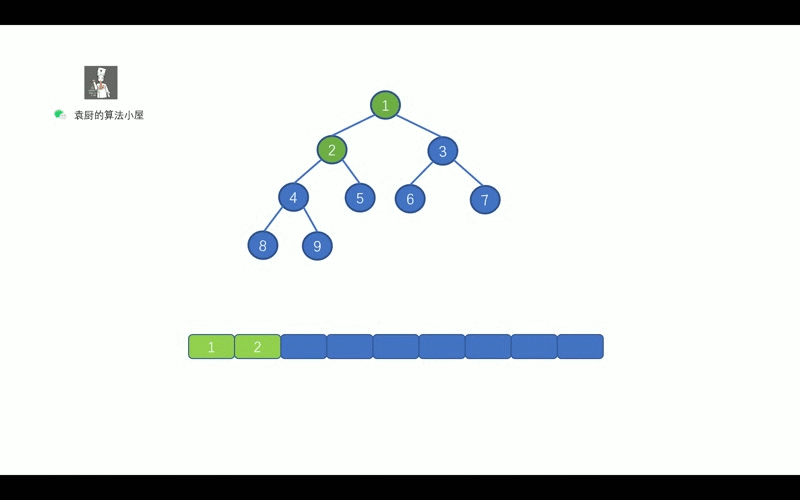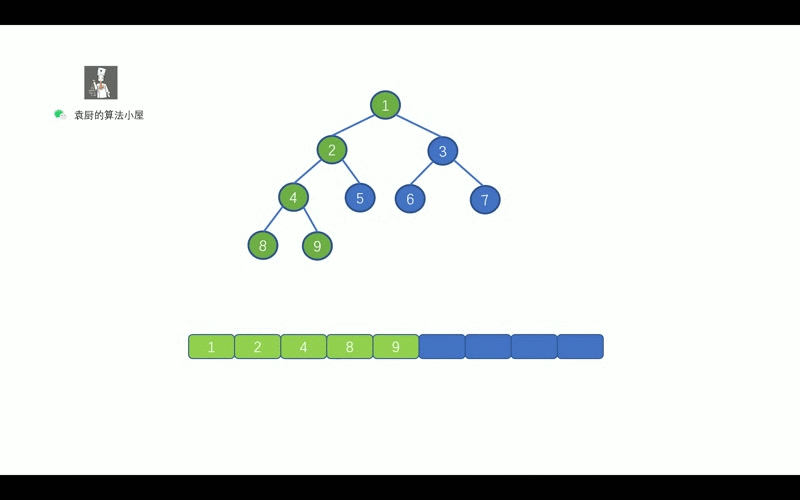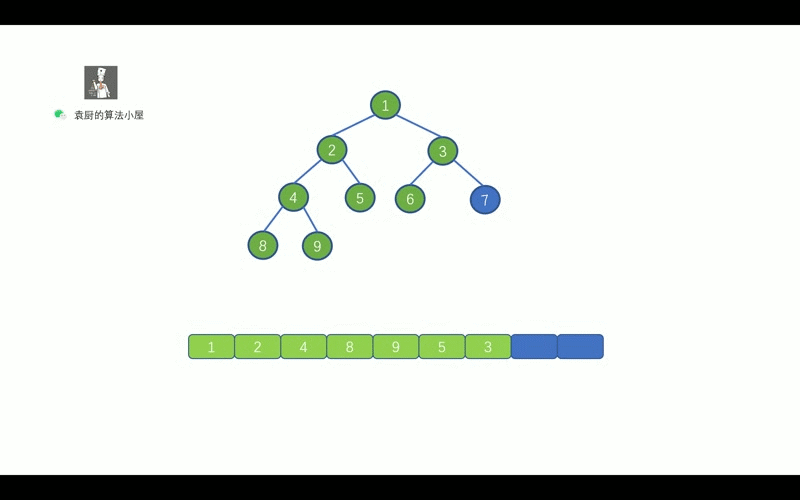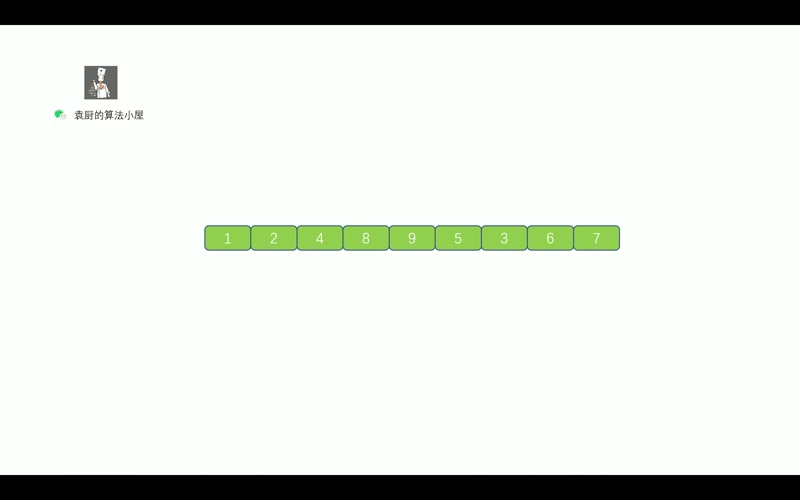
前序遍历的顺序是, 对于树中的某节点,先遍历该节点,然后再遍历其左子树,最后遍历其右子树.
我们先来通过下面这个动画复习一下二叉树的前序遍历。
迭代
我们试想一下,之前我们借助队列帮我们实现二叉树的层序遍历,
那么可不可以,也借助数据结构,帮助我们实现二叉树的前序遍历。
见下图
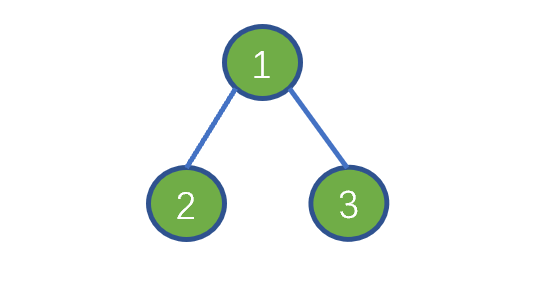
假设我们的二叉树为 [1,2,3]。我们需要对其进行前序遍历。其遍历顺序为
当前节点 1,左孩子 2,右孩子 3。
这里可不可以用栈,帮我们完成前序遍历呢?
栈和队列的那些事
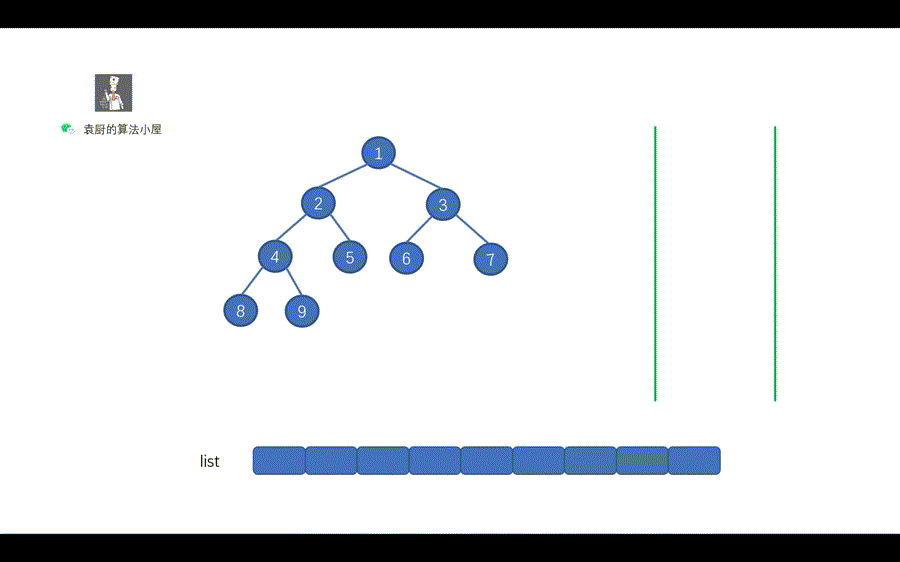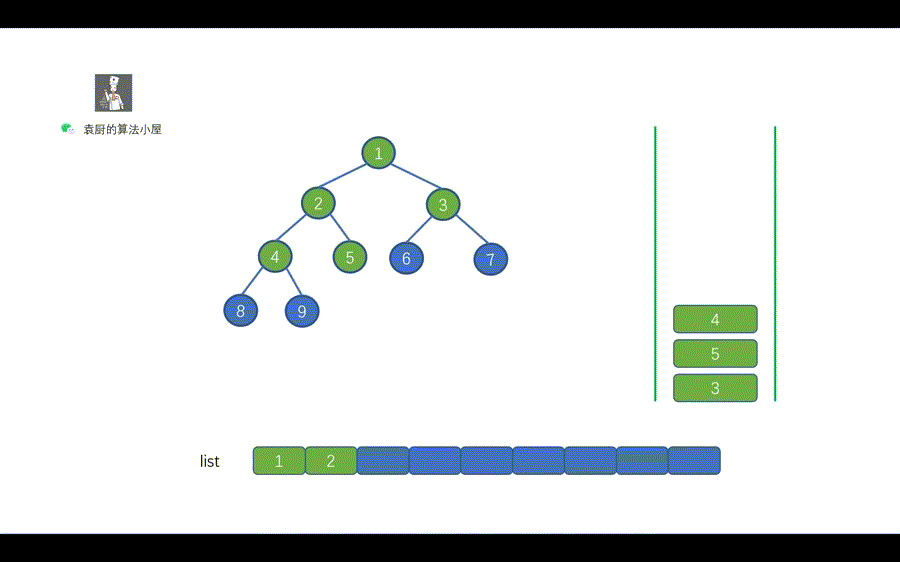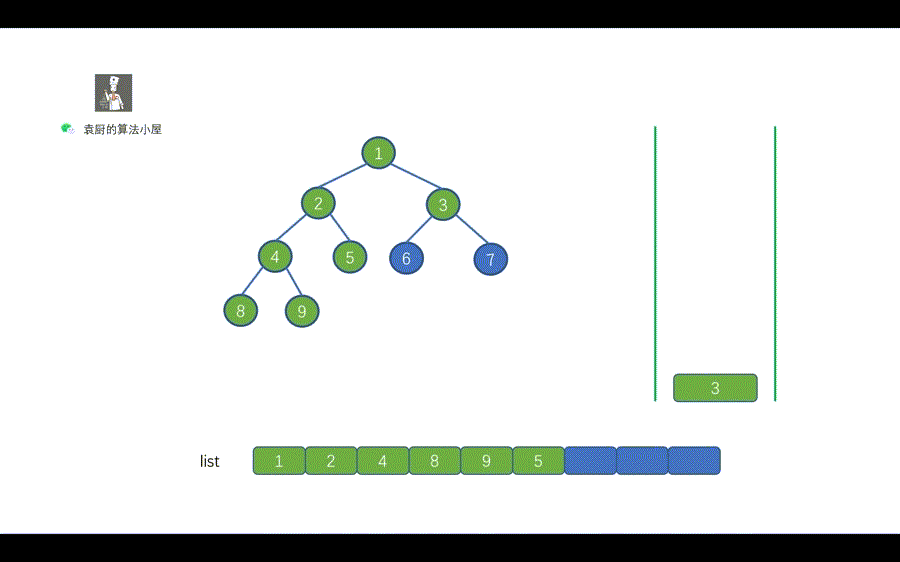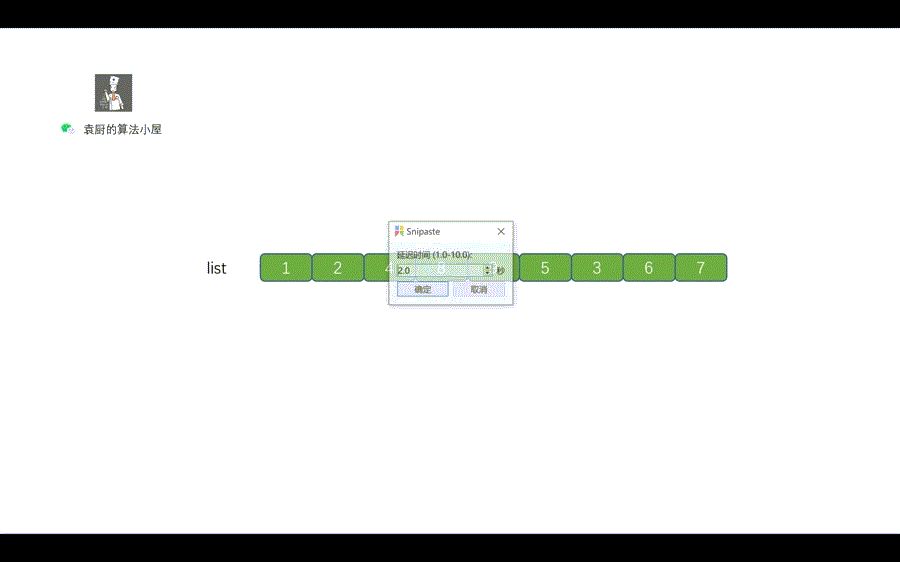
我们都知道栈的特性是先进后出,我们借助栈来帮助我们完成前序遍历的时候。
则需要注意的一点是,我们应该先将右子节点入栈,再将左子节点入栈。
这样出栈时,则会先出左节点,再出右子节点,则能够完成树的前序遍历。
见下图。
我们用一句话对上图进行总结,当栈不为空时,栈顶元素出栈,如果其右孩子不为空,则右孩子入栈,其左孩子不为空,则左孩子入栈。还有一点需要注意的是,我们和层序遍历一样,需要先将 root 节点进行入栈,然后再执行 while 循环。
看到这里你已经能够自己编写出代码了,不信你去试试。
时间复杂度:O(n) 需要对所有节点遍历一次
空间复杂度:O(n) 栈的开销,平均为 O(logn) 最快情况,即斜二叉树时为 O(n)
参考代码
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if (root == null) return list;
stack.push(root);
while (!stack.isEmpty()) {
TreeNode temp = stack.pop();
if (temp.right != null) {
stack.push(temp.right);
}
if (temp.left != null) {
stack.push(temp.left);
}
//这里也可以放到前面
list.add(temp.val);
}
return list;
}
}
Swift Code:
class Solution {
func preorderTraversal(_ root: TreeNode?) -> [Int] {
var list:[Int] = []
var stack:[TreeNode] = []
guard root != nil else {
return list
}
stack.append(root!)
while !stack.isEmpty {
let temp = stack.popLast()
if let right = temp?.right {
stack.append(right)
}
if let left = temp?.left {
stack.append(left)
}
//这里也可以放到前面
list.append((temp?.val)!)
}
return list
}
}
Go Code:
func preorderTraversal(root *TreeNode) []int {
res := []int{}
if root == nil {
return res
}
stk := []*TreeNode{root}
for len(stk) != 0 {
temp := stk[len(stk) - 1]
stk = stk[: len(stk) - 1]
if temp.Right != nil {
stk = append(stk, temp.Right)
}
if temp.Left != nil {
stk = append(stk, temp.Left)
}
res = append(res, temp.Val)
}
return res
}