algorithm-base/animation-simulation/数组篇/leetcode41缺失的第一个正数.md

如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友 tan45du_one ，备注 github + 题目 + 问题 向我反馈

感谢支持，该仓库会一直维护，希望对各位有一丢丢帮助。

另外希望手机阅读的同学可以来我的 公众号：袁厨的算法小屋 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击刷题小队进入。

41. 缺失的第一个正数

给你一个未排序的整数数组，请你找出其中没有出现的最小的正整数。

示例 1:

输入: [1,2,0] 输出: 3

示例 2:

输入: [3,4,-1,1] 输出: 2

示例 3:

输入: [7,8,9,11,12] 输出: 1

重复遍历

让我们找出缺失的最小正整数，而且这是一个未排序的数组，我们可以利用暴力求解，挨个遍历发现那个不存在直接返回即可。我们这里使用两种方法解决这个问题，大家也可以提出自己的做法。

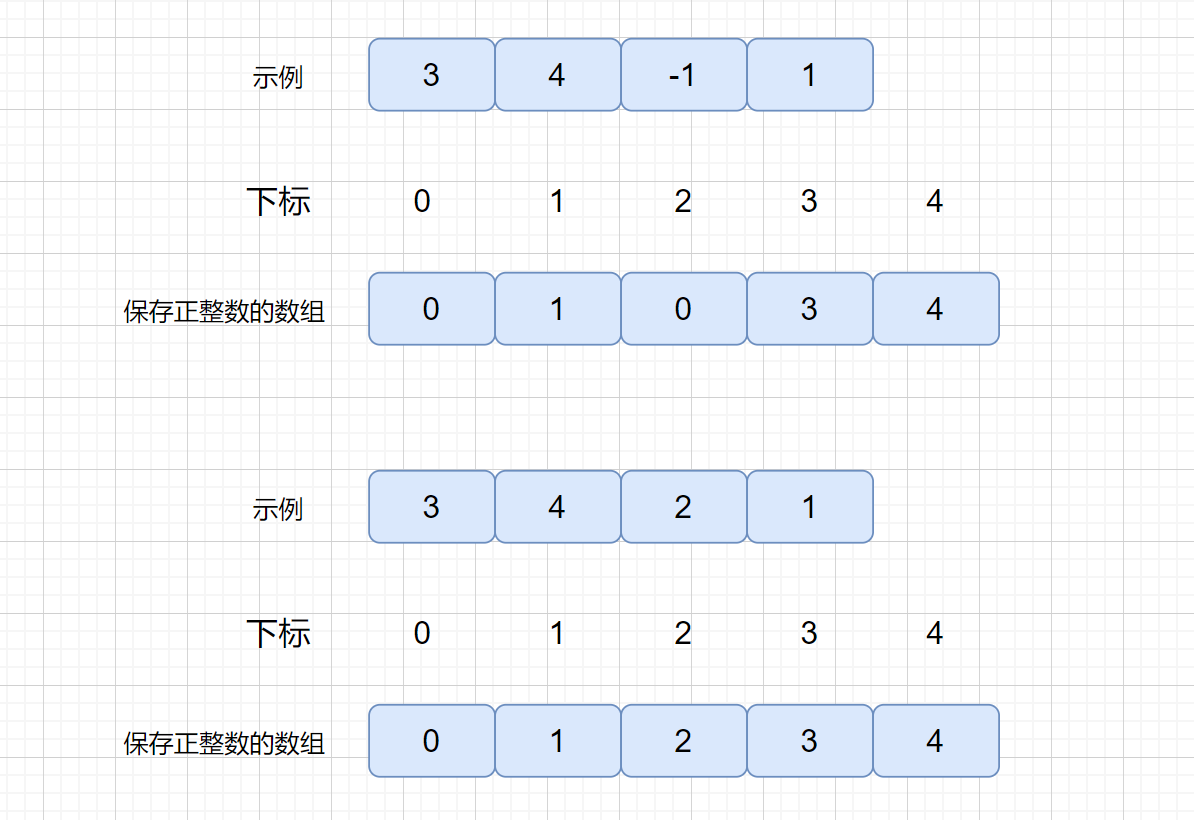
我们既然是返回缺失的正整数，那么我们则可以将这个数组中的所有正整数保存到相应的位置，见下图。

上图中，我们遍历一遍原数组，将正整数保存到新数组中，然后遍历新数组，第一次发现 newnum[i] != i 时，则说明该值是缺失的，返回即可，例如我上图中的第一个示例中的 2，如果遍历完新数组，发现说所有值都对应，说明缺失的是 新数组的长度对应的那个数，比如第二个示例中 ，新数组的长度为 5，此时缺失的为 5，返回长度即可，很容易理解。

注：我们发现我们新的数组长度比原数组大 1，是因为我们遍历新数组从 1，开始遍历。

动图解析

Java Code:

class Solution {
    public int firstMissingPositive(int[] nums) {
        if (nums.length == 0) {
            return 1;
        }
        //因为是返回第一个正整数，不包括 0，所以需要长度加1，细节1
        int[] res = new int[nums.length + 1];
        //将数组元素添加到辅助数组中
        for (int x : nums) {
            if (x > 0 && x < res.length) {
               res[x] = x;
            }
        }
        //遍历查找,发现不一样时直接返回
        for (int i = 1; i < res.length; i++) {
            if (res[i] != i) {
                return i;
            }
        }
        //缺少最后一个，例如 1，2，3此时缺少 4 ，细节2
        return res.length;
    }
}

Python3 Code:

from typing import List
class Solution:
    def firstMissingPositive(self, nums: List[int])->int:
        if len(nums) == 0:
            return 1
        # 因为是返回第一个正整数，不包括 0，所以需要长度加1，细节1
        res = [0] * (len(nums) + 1)
        # 将数组元素添加到辅助数组中
        for x in nums:
            if x > 0 and x < len(res):
                res[x] = x
        # 遍历查找,发现不一样时直接返回
        for i in range(1, len(res)):
            if res[i] != i:
                return i
        # 缺少最后一个，例如 1，2，3此时缺少 4 ，细节2
        return len(res)

Swift Code

class Solution {
    func firstMissingPositive(_ nums: [Int]) -> Int {
        if nums.count == 0 {
            return 1
        }
        // 因为是返回第一个正整数，不包括 0，所以需要长度加1，细节1
        var res:[Int] = Array.init(repeating: 0, count: nums.count + 1)
        // 将数组元素添加到辅助数组中
        for x in nums {
            if x > 0 && x < res.count {
                res[x] = x
            }
        }
        // 遍历查找,发现不一样时直接返回
        for i in 1..<res.count {
            if res[i] != i {
                return i
            }
        }
        // 缺少最后一个，例如 1，2，3此时缺少 4 ，细节2
        return res.count
    }
}

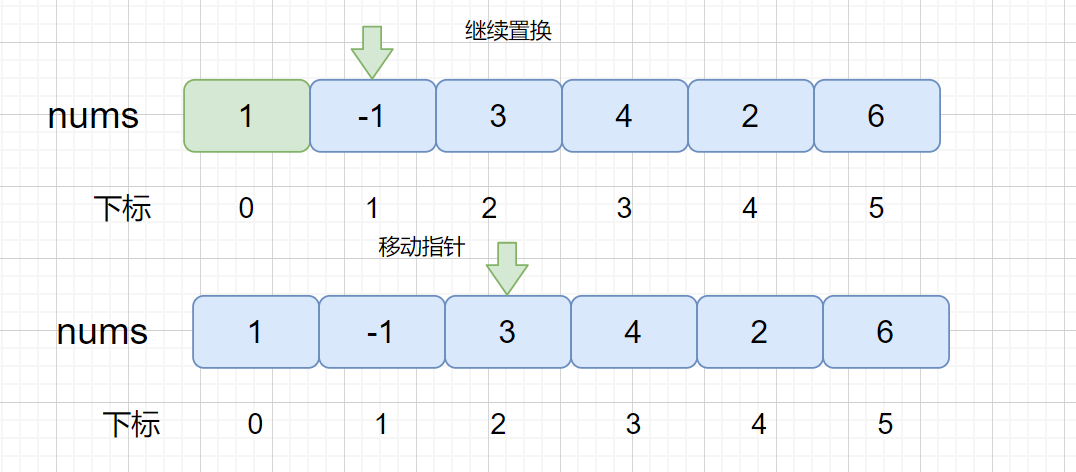
我们通过上面的例子了解这个解题思想，我们有没有办法不使用辅助数组完成呢？我们可以使用原地置换，直接在 nums 数组内，将值换到对应的索引处，与上个方法思路一致，只不过没有使用辅助数组，理解起来也稍微难理解一些。

下面我们看一下原地置换的一些情况。

注：红色代表待置换，绿色代表置换完毕

动图解析：

题目代码：

Java Code:

class Solution {
    public int firstMissingPositive(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 1;
        }
        for (int i = 0; i < len; ++i) {
            //需要考虑指针移动情况，大于0，小于len+1，不等与i+1，两个交换的数相等时，防止死循环
            while (nums[i] > 0 && nums[i] < len + 1 && nums[i] != i+1 && nums[i] != nums[nums[i]-1]) {
                swap(nums,i,nums[i] - 1);
            }
        }
        //遍历寻找缺失的正整数
        for (int i = 0; i < len; ++i) {
            if(nums[i] != i+1) {
                return i+1;
            }
        }
        return len + 1;
    }
    //交换
   public void swap(int[] nums, int i, int j) {
        if (i != j) {
            nums[i] ^= nums[j];
            nums[j] ^= nums[i];
            nums[i] ^= nums[j];
        }
    }
}

Python3 Code:

class Solution:
    def firstMissingPositive(self, nums: List[int]) -> int:
        n = len(nums)

        def swap(nums, a, b):
            temp = nums[a]
            nums[a] = nums[b]
            nums[b] = temp
        i = 0
        while i < n:
            num = nums[i]
            # 已经就位
            if num <= 0 or num >= n or num == i + 1 or nums[num - 1] == num:
                i += 1
            # 可以交换
            else:
                swap(nums, i, num - 1)
        for i in range(n):
            if nums[i] != i + 1:
                return i + 1
        return n + 1

Swift Code

class Solution {
    func firstMissingPositive(_ nums: [Int]) -> Int {
        var nums = nums
        let len = nums.count
        if len == 0 {
            return 1
        }
        // 遍历数组
        for i in 0..<len {
            // 需要考虑指针移动情况，大于0，小于len+1，不等与i+1，
            // 两个交换的数相等时，防止死循环
            while nums[i] > 0
                  && nums[i] < len + 1
                  && nums[i] != i + 1
                  && nums[i] != nums[nums[i] - 1]
            {
                //nums.swapAt(i, (nums[i] - 1)) // 系统方法
                self.swap(&nums, i, (nums[i] - 1)) // 自定义方法
            }
        }
        // 遍历寻找缺失的正整数
        for i in 0..<len {
            if nums[i] != i + 1 {
                return i + 1
            }
        }

        return len + 1
    }
    func swap(_ nums: inout [Int], _ i: Int, _ j: Int) {
        let temp = nums[i]
        nums[i] = nums[j]
        nums[j] = temp
    }
}

C++ Code

class Solution
{
public:
    int firstMissingPositive(vector<int> &nums)
    {
        int size = nums.size();
        //判断范围是否符合要求
        auto inRange = [](auto s, auto e)
        {
            return [s, e](auto &n)
            {
                return e >= n && n >= s;
            };
        };
        auto cusInRange = inRange(1, size);
        //增加数组长度, 便于计算, 不需要再转换
        nums.push_back(0);

        for (int i = 0; i < size; i++)
        {
            //将不在正确位置的元素放到正确位置上
            while (cusInRange(nums[i]) && nums[i] != i && nums[nums[i]] != nums[i])
            {
                swap(nums[i], nums[nums[i]]);
            }
        }

        //找出缺失的元素
        for (int i = 1; i <= size; i++)
        {
            if (nums[i] != i)
                return i;
        }
        return size + 1;
    }
};

Go Code:

func firstMissingPositive(nums []int) int {
    length := len(nums)
    if length == 0 { return 1 }
    for i := 0; i < length; i++ {
        // 将不在正确位置的元素放在正确的位置上。
        for nums[i] > 0 && nums[i] < length + 1 && nums[i] != i + 1 && nums[i] != nums[nums[i] - 1] {
            j := nums[i] - 1
            nums[i], nums[j] = nums[j], nums[i]
        }
    }
	// 第一个不在正确位置上的元素就是结果。
    for i := 0; i < length; i++ {
        if nums[i] != i + 1 {
            return i + 1
        }
    }
    return length + 1
}