mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-20 02:53:39 +00:00
150 lines
4.7 KiB
Markdown
150 lines
4.7 KiB
Markdown
|
||
|
||
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||
>
|
||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||
>
|
||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||
|
||
### [59.螺旋矩阵 II](https://leetcode-cn.com/problems/spiral-matrix-ii)
|
||
|
||
给你一个正整数 `n` ,生成一个包含 `1` 到 `n2` 所有元素,且元素按顺时针顺序螺旋排列的 `n x n` 正方形矩阵 `matrix` 。
|
||
|
||
**示例 1:**
|
||
|
||
> 输入:n = 3
|
||
> 输出:[[1,2,3],[8,9,4],[7,6,5]]
|
||
|
||
**示例 2:**
|
||
|
||
> 输入:n = 1
|
||
> 输出:[[1]]
|
||
|
||
其实我们只要做过了螺旋矩阵 第一题,这个题目我们完全可以一下搞定,几乎没有进行更改,我们先来看下 **leetcode 54** 题的解析。
|
||
|
||
|
||
|
||
### leetcode 54 螺旋矩阵
|
||
|
||
题目描述
|
||
|
||
*给定一个包含 m* x n个元素的矩阵(m 行, n 列),请按照顺时针螺旋顺序,返回矩阵中的所有元素。
|
||
|
||
|
||
|
||
示例一
|
||
|
||
> 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
|
||
> 输出:[1,2,3,6,9,8,7,4,5]
|
||
|
||
示例二
|
||
|
||
> 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
|
||
> 输出:[1,2,3,4,8,12,11,10,9,5,6,7]
|
||
|
||
|
||
|
||
这个题目很细非常细,思路很容易想到,但是要是完全实现也不是特别容易,我们一起分析下这个题目,我们可以这样理解,我们像剥洋葱似的一步步的剥掉外皮,直到遍历结束,见下图。
|
||
|
||
|
||
|
||
*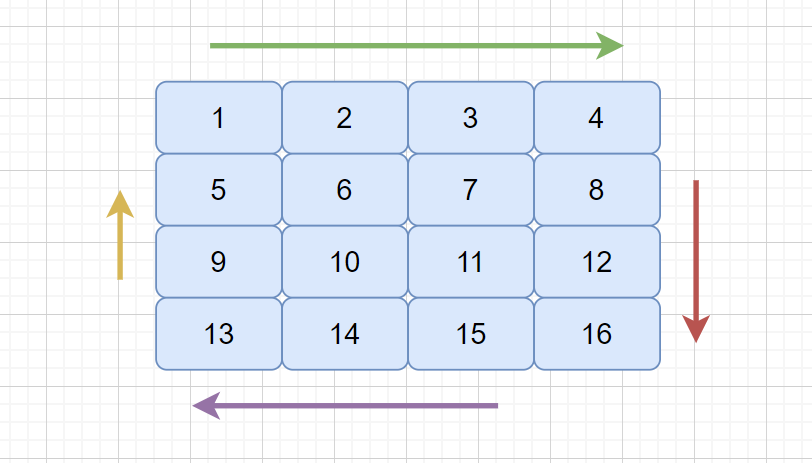*
|
||
|
||
|
||
|
||
题目很容易理解,但是要想完全执行出来,也是不容易的,因为这里面的细节太多了,我们需要认真仔细的考虑边界。
|
||
|
||
|
||
|
||
我们也要考虑重复遍历的情况即什么时候跳出循环。刚才我们通过箭头知道了我们元素的遍历顺序,这个题目也就完成了一大半了,下面我们来讨论一下什么时候跳出循环,见下图。
|
||
|
||
|
||
|
||
注:这里需要注意的是,框框代表的是每个边界。
|
||
|
||

|
||
|
||
题目代码:
|
||
|
||
```java
|
||
class Solution {
|
||
public List<Integer> spiralOrder(int[][] matrix) {
|
||
|
||
List<Integer> arr = new ArrayList<>();
|
||
int left = 0, right = matrix[0].length-1;
|
||
int top = 0, down = matrix.length-1;
|
||
|
||
while (true) {
|
||
for (int i = left; i <= right; ++i) {
|
||
arr.add(matrix[top][i]);
|
||
}
|
||
top++;
|
||
if (top > down) break;
|
||
for (int i = top; i <= down; ++i) {
|
||
arr.add(matrix[i][right]);
|
||
}
|
||
right--;
|
||
if (left > right) break;
|
||
for (int i = right; i >= left; --i) {
|
||
arr.add(matrix[down][i]);
|
||
}
|
||
down--;
|
||
if (top > down) break;
|
||
for (int i = down; i >= top; --i) {
|
||
arr.add(matrix[i][left]);
|
||
}
|
||
left++;
|
||
if (left > right) break;
|
||
|
||
}
|
||
return arr;
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
|
||
|
||
我们仅仅是将 54 反过来了,往螺旋矩阵里面插值,下面我们直接看代码吧,大家可以也可以对其改进,大家可以思考一下,如果修改能够让代码更简洁!
|
||
|
||
```java
|
||
class Solution {
|
||
public int[][] generateMatrix(int n) {
|
||
|
||
int[][] arr = new int[n][n];
|
||
int left = 0;
|
||
int right = n-1;
|
||
int top = 0;
|
||
int buttom = n-1;
|
||
int num = 1;
|
||
int numsize = n*n;
|
||
while (true) {
|
||
for (int i = left; i <= right; ++i) {
|
||
arr[top][i] = num++;
|
||
}
|
||
top++;
|
||
if (num > numsize) break;
|
||
for (int i = top; i <= buttom; ++i) {
|
||
arr[i][right] = num++;
|
||
|
||
}
|
||
right--;
|
||
if (num > numsize) break;
|
||
for (int i = right; i >= left; --i) {
|
||
arr[buttom][i] = num++;
|
||
}
|
||
buttom--;
|
||
if (num > numsize) break;
|
||
for (int i = buttom; i >= top; --i) {
|
||
arr[i][left] = num++;
|
||
}
|
||
left++;
|
||
if (num > numsize) break;
|
||
|
||
}
|
||
return arr;
|
||
}
|
||
}
|
||
```
|
||
|