mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-01 09:43:38 +00:00
70 lines
3.5 KiB
Markdown
70 lines
3.5 KiB
Markdown
### **leetcode 523 连续的子数组和**
|
||
|
||
**题目描述**
|
||
|
||
> 给定一个包含 非负数 的数组和一个目标 整数 k,编写一个函数来判断该数组是否含有连续的子数组,其大小至少为 2,且总和为 k 的倍数,即总和为 n*k,其中 n 也是一个整数。
|
||
|
||
**示例 1:**
|
||
|
||
> 输入:[23,2,4,6,7], k = 6
|
||
> 输出:True
|
||
|
||
解释:[2,4] 是一个大小为 2 的子数组,并且和为 6。
|
||
|
||
**示例 2:**
|
||
|
||
> 输入:[23,2,6,4,7], k = 6
|
||
> 输出:True
|
||
|
||
解释:[23,2,6,4,7]是大小为 5 的子数组,并且和为 42。
|
||
|
||
**前缀和 + HashMap**
|
||
|
||
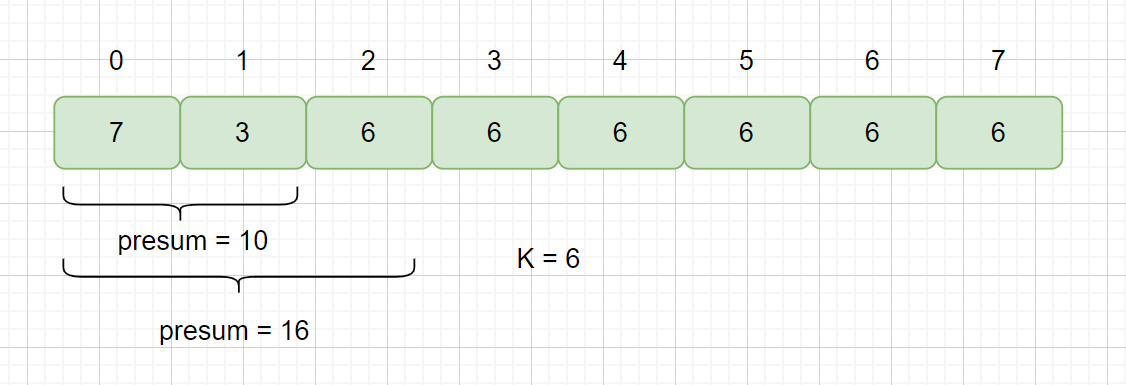
这个题目算是对刚才那个题目的升级,前半部分是一样的,都是为了让你找到能被 K 整除的子数组,但是这里加了一个限制,那就是子数组的大小至少为 2,那么我们应该怎么判断子数组的长度呢?我们可以根据索引来进行判断,见下图。
|
||
|
||
|
||
|
||
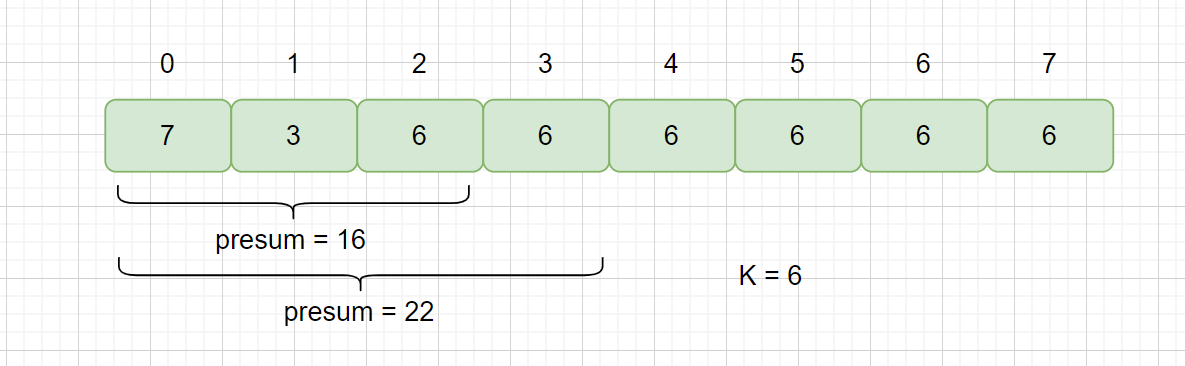
此时我们 K = 6, presum % 6 = 4 也找到了相同余数的前缀子数组 [0,1] 但是我们此时指针指向为 2,我们的前缀子区间 [0,1]的下界为1,所以 2 - 1 = 1,但我们的中间区间的长度小于2,所以不能返回 true,需要继续遍历,那我们有两个区间[0,1],[0,2]都满足 presum % 6 = 4,那我们哈希表中保存的下标应该是 1 还是 2 呢?我们保存的是1,如果我们保存的是较大的那个索引,则会出现下列情况,见下图。
|
||
|
||
|
||
|
||
此时,仍会显示不满足子区间长度至少为 2 的情况,仍会继续遍历,但是我们此时的 [2,3]区间已经满足该情况,返回 true,所以我们往哈希表存值时,只存一次,即最小的索引即可。下面我们看一下该题的两个细节
|
||
|
||
细节1:我们的 k 如果为 0 时怎么办,因为 0 不可以做除数。所以当我们 k 为 0 时可以直接存到数组里,例如输入为 [0,0] , K = 0 的情况
|
||
|
||
细节2:另外一个就是之前我们都是统计个数,value 里保存的是次数,但是此时我们加了一个条件就是长度至少为 2,保存的是索引,所以我们不能继续 map.put(0,1),应该赋初值为 map.put(0,-1)。这样才不会漏掉一些情况,例如我们的数组为[2,3,4],k = 1,当我们 map.put(0,-1) 时,当我们遍历到 nums[1] 即 3 时,则可以返回 true,因为 1-(-1)= 2,5 % 1=0 , 同时满足。
|
||
|
||
**视频解析**
|
||
|
||

|
||
|
||
**题目代码**
|
||
|
||
```java
|
||
class Solution {
|
||
public boolean checkSubarraySum(int[] nums, int k) {
|
||
HashMap<Integer,Integer> map = new HashMap<>();
|
||
//细节2
|
||
map.put(0,-1);
|
||
int presum = 0;
|
||
for (int i = 0; i < nums.length; ++i) {
|
||
presum += nums[i];
|
||
//细节1,防止 k 为 0 的情况
|
||
int key = k == 0 ? presum : presum % k;
|
||
if (map.containsKey(key)) {
|
||
if (i - map.get(key) >= 2) {
|
||
return true;
|
||
}
|
||
//因为我们需要保存最小索引,当已经存在时则不用再次存入,不然会更新索引值
|
||
continue;
|
||
}
|
||
map.put(key,i);
|
||
}
|
||
return false;
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|