algorithm-base/animation-simulation/数据结构和算法/堆排序.md

堆排序

如果阅读时，发现错误，或者动画不可以显示的问题可以添加我微信好友 tan45du_one ，备注 github + 题目 + 问题 向我反馈

感谢支持，该仓库会一直维护，希望对各位有一丢丢帮助。

另外希望手机阅读的同学可以来我的 公众号：袁厨的算法小屋 两个平台同步，想要和题友一起刷题，互相监督的同学，可以在我的小屋点击刷题小队进入。

说堆排序之前，我们先简单了解一些什么是堆？堆这种数据结构应用场景非常多，所以我们需要熟练掌握呀！

那我们了解堆之前，先来简单了解下，什么是完全二叉树？

我们来看下百度百科的定义，完全二叉树：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。

哦！我们可以这样理解，除了最后一层，其他层的节点个数都是满的，而且最后一层的叶子节点必须靠左。

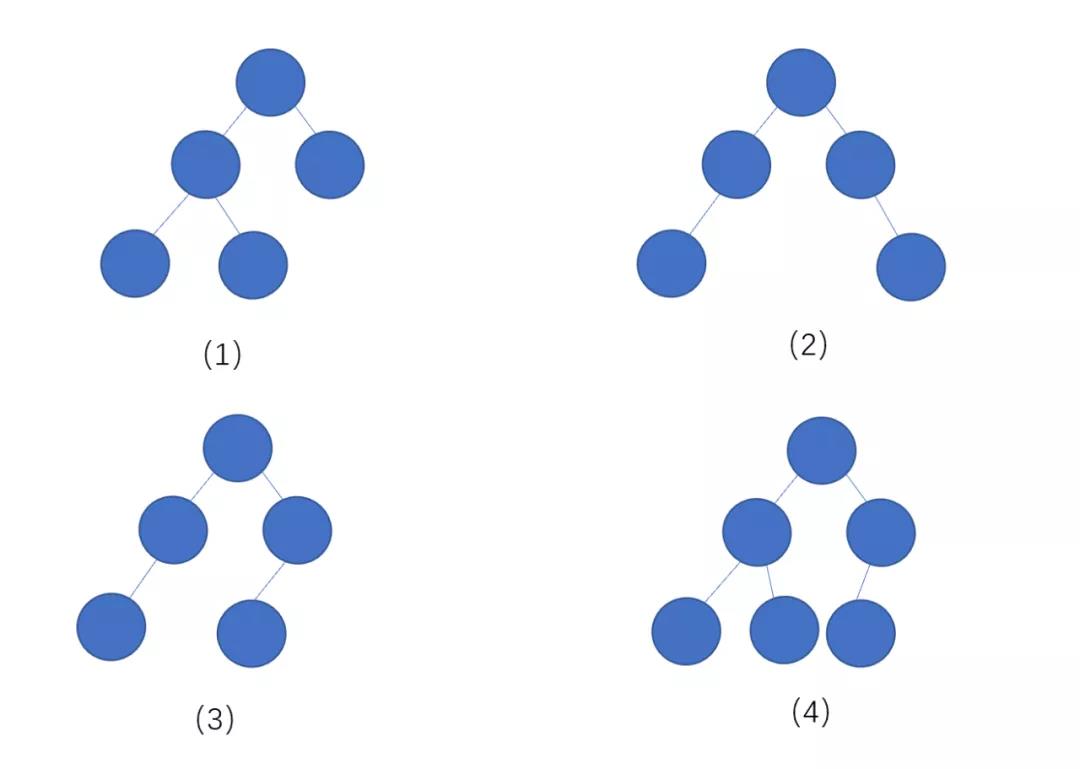
下面我们来看一下这几个例子

上面的几个例子中，（1）（4）为完全二叉树，（2）（3）不是完全二叉树，通过上面的几个例子，我们了解了什么是完全二叉树，

那么堆到底是什么呢？

下面我们来看一下二叉堆的要求

（1）必须是完全二叉树

（2）二叉堆中的每一个节点，都必须大于等于（或小于等于）其子树中每个节点的值。

若是每个节点大于等于子树中的每个节点，我们称之为大顶堆，小于等于子树中的每个节点，我们则称之为小顶堆。见下图

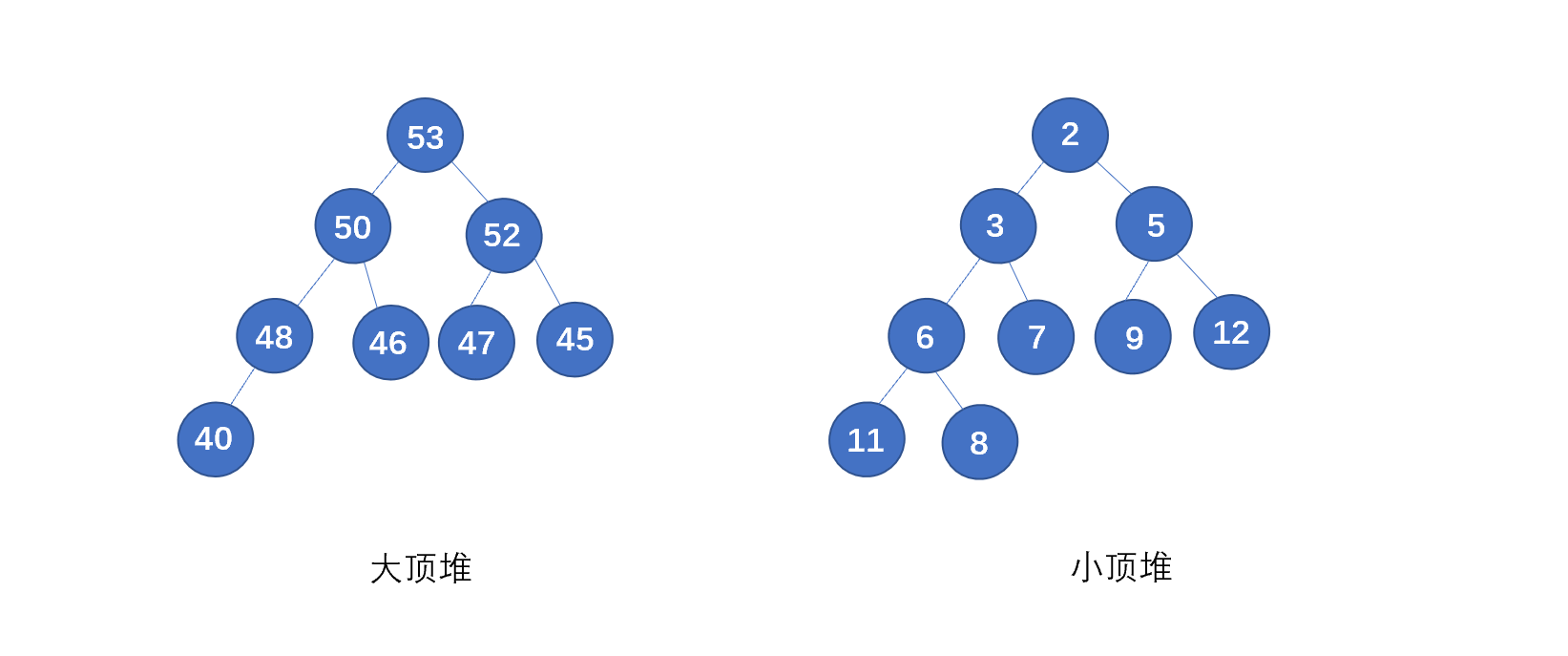
下面我们再来看一下二叉堆的具体例子。

上图则为大顶堆和小顶堆，我们再来回顾一下堆的要求，看下是否符合

（1）必须是完全二叉树

（2）堆中的每一个节点，都必须大于等于（或小于等于）其子树中每个节点的值。

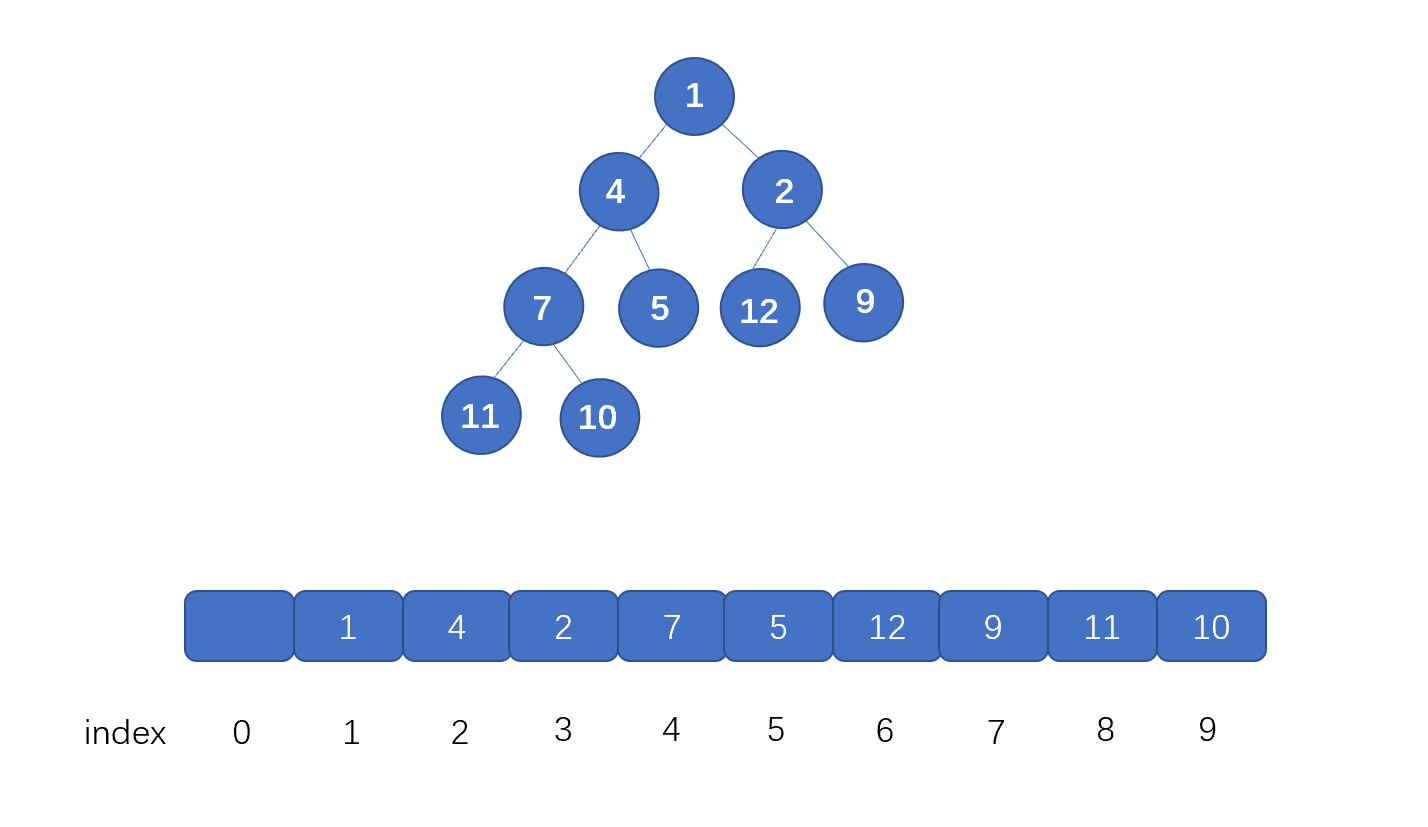
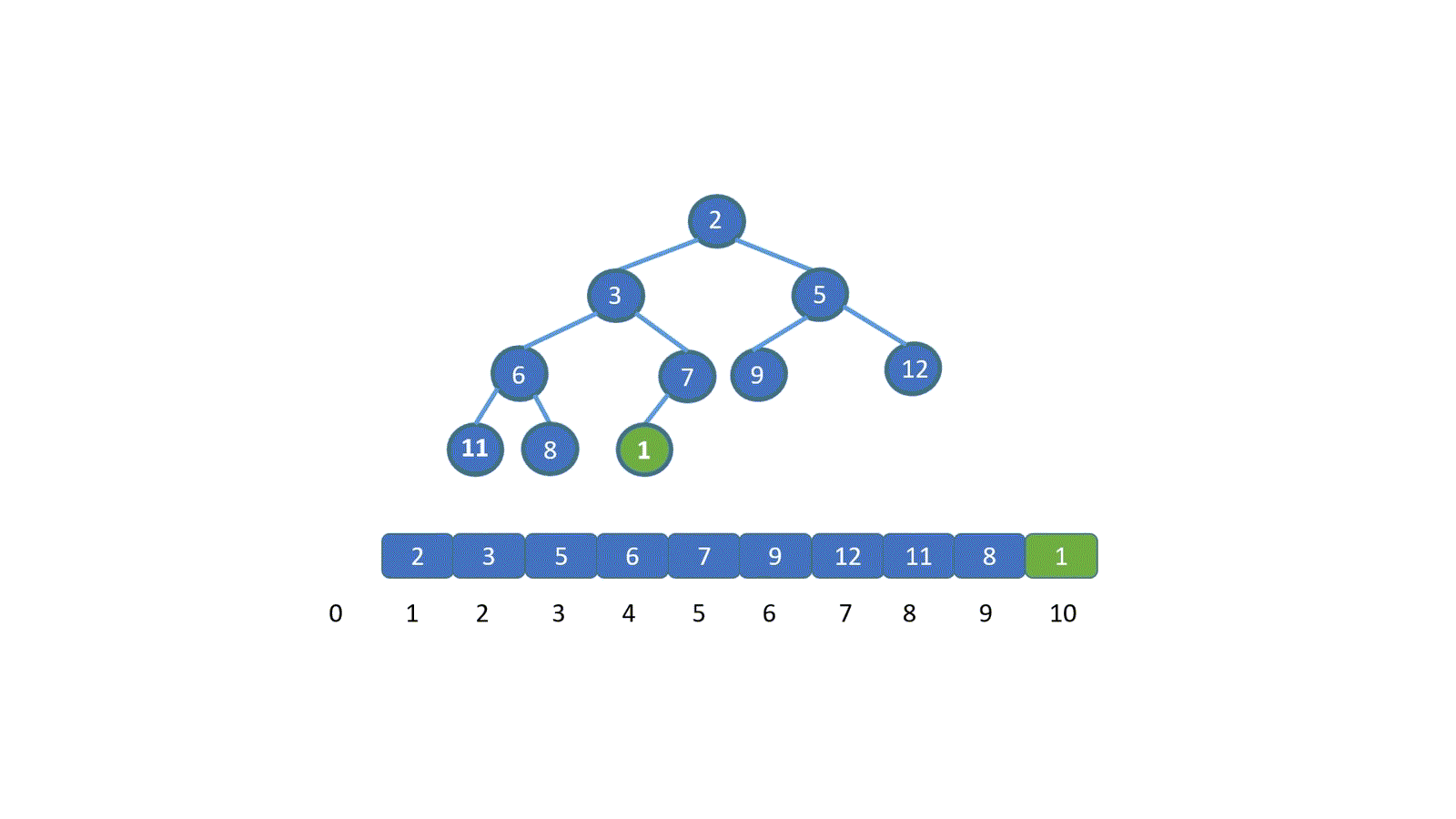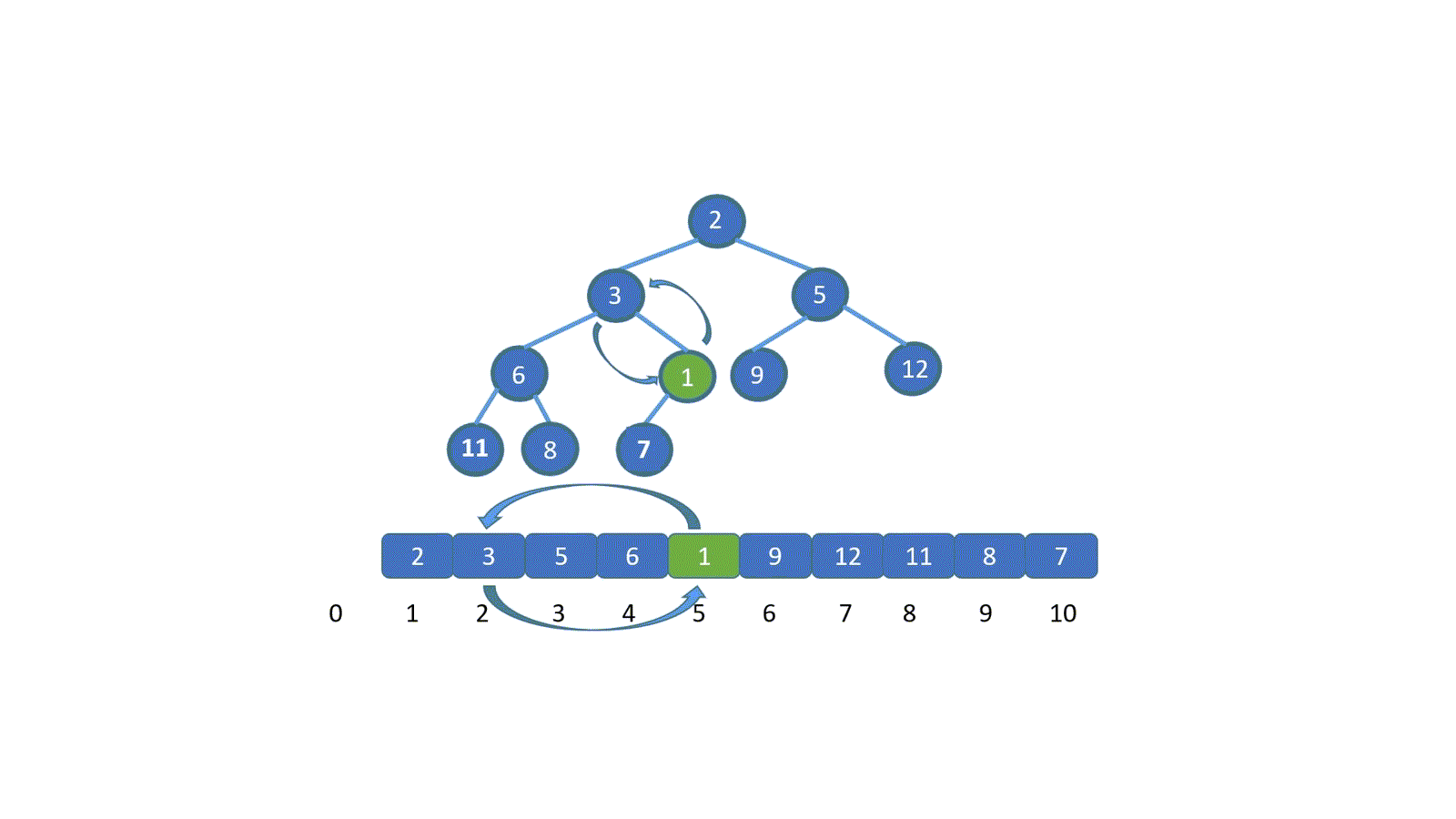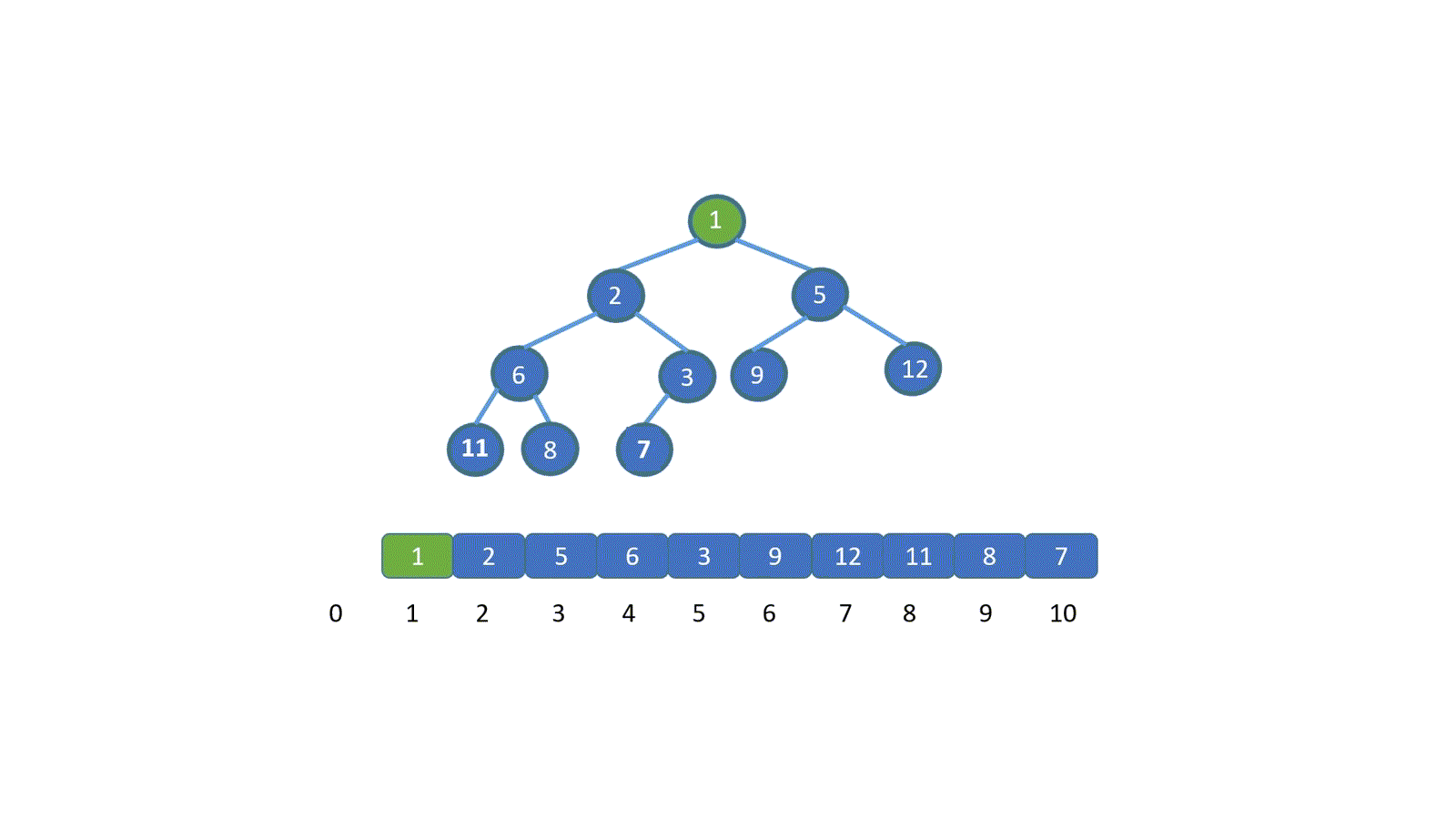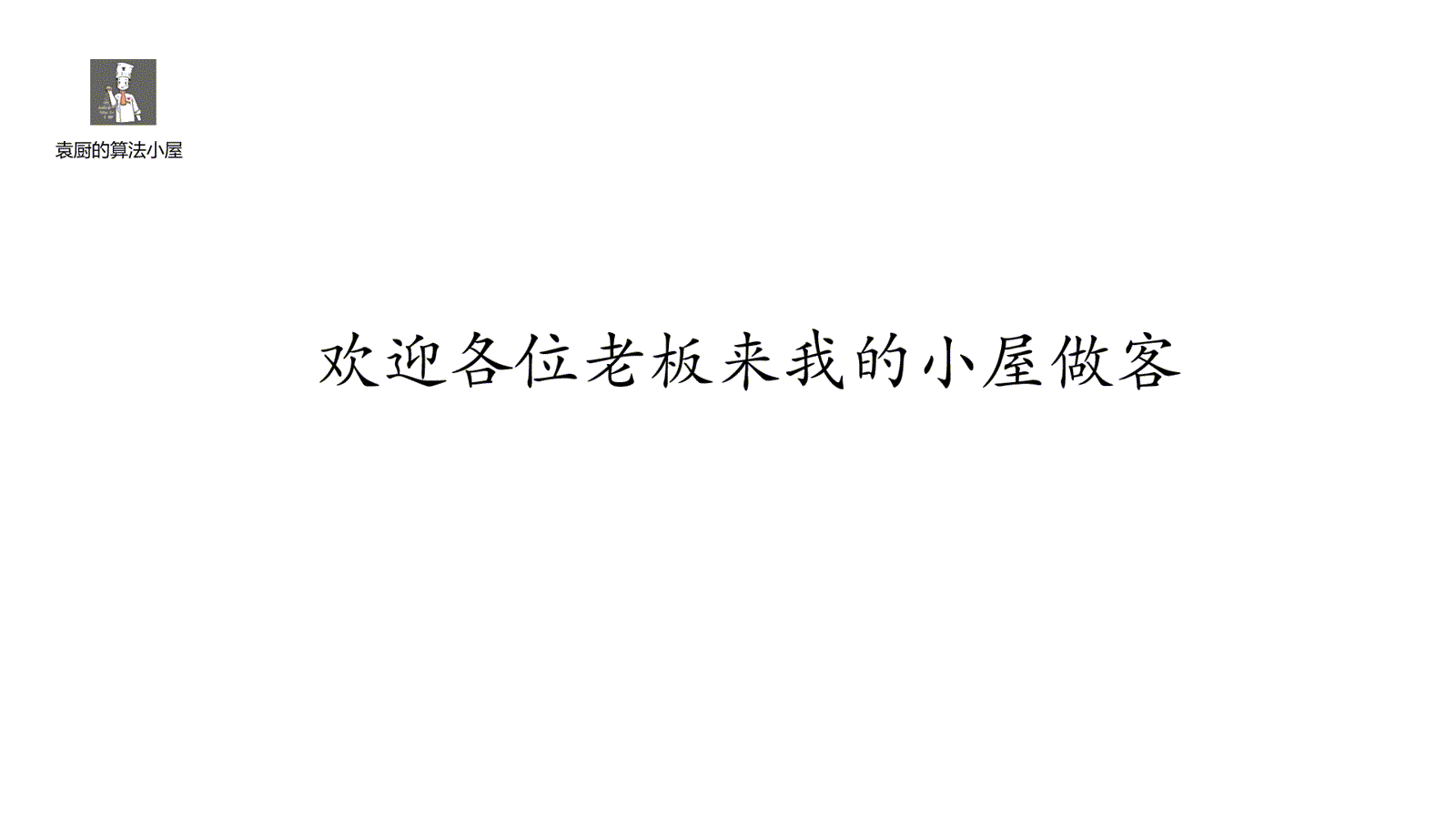
好啦，到这里我们已经完全掌握二叉堆了，那么二叉堆又是怎么存储的呢？因为堆是完全二叉树，所以我们完全可以用数组存储。具体思想见下图，我们仅仅按照顺序将节点存入数组即可，我们通过小顶堆进行演示。

注：我们是从下标 1 开始存储的，这样能省略一些计算，下文中我们将二叉堆简称为堆

我们来看一下为什么我们可以用数组来存储堆呢？

我们首先看根节点，也就是值为 1 的节点，它在数组中的下标为 1 ,它的左子节点，也就是值为 4 的节点，此时索引为 2，右子节点也就是值为 2 的节点，它的索引为 3。

我们发现其中的关系了吗？

数组中，某节点（非叶子节点）的下标为 i , 那么其左子节点下标为 2*i （这里可以直接通过相乘得到左孩子，如果从0 开始存，需要 2i+1 才行）, 右子节点为 2i+1**，**其父节点为 i/2 。既然我们完全可以根据索引找到某节点的 左子节点 和 右子节点，那么我们用数组存储是完全没有问题的。

好啦，我们知道了什么是堆和如何用数组存储堆，那我们如何完成堆排序呢？

堆排序其实主要有两个步骤

• 建堆
• 排序

下面我们先来了解下建堆

我们刚才说了用数组来存储大顶（小顶）堆，此时的元素已经满足某节点大于等于（或小于等于）子树节点，但是随机给我们一个数组，此时并不一定满足上诉要求，所以我们需要调整数组，使其满足大顶堆或小顶堆的要求。这个就是堆化，也可以称其为建堆。

建堆我们这里提出两种方法，利用上浮操作，也就是不断插入元素进行建堆，另一种是利用下沉操作，遍历父节点，不断将其下沉，进行建堆，我们一起来看吧。

我们先来说下第一种建堆方式

利用上浮操作建堆

说之前我们先来了解下，如何往已经建好的堆里，插入新的元素，我们直接看例子吧，一下就懂啦。

假设让我们插入新的元素 1 （绿色节点），我们发现此时 1 小于其父节点 的值 7 ，并不遵守小顶堆的规则，那我们则需要移动元素 1 。让 1 与 7 交换，（如果新插入元素大于父节点的值，则说明插入新节点后仍满足小顶堆规则，无需交换）。

之前我们说过，我们可以用数组保存堆，并且可以通过 i/2 得到其父节点的值，那么此时我们就明白怎么做啦。

将插入节点与其父节点，交换。

交换之后，我们继续将新插入元素，也就是 1 与其父节点比较，如果大于其父节点，则无需交换，循环结束。若小于则需要继续交换，直到 1 到达适合他的地方。大家是不是已经直到该怎么做啦！下面我们直接看动图吧。

看完动图是不是就妥了，其实很简单，我们只需将新加入元素与其父节点比较，判断是否小于堆顶元素（小顶堆），如果小于则进行交换，（让更小的节点为父节点）直到符合堆的规则位置，大顶堆则相反。

我们发现，我们新插入的元素是不是一层层的上浮，直到找到属于自己的位置，我们将这个操作称之为上浮操作。

那我们知道了上浮，岂不是就可以实现建堆了？是的，我们则可以依次遍历数组，就好比不断往堆中插入新元素，直至遍历结束，这样我们就完成了建堆，这种方法当然是可以的。

我们一起来看一下上浮操作代码。

public void swim (int index) {
    while (index > 1 && nums[index/2] > nums[index]) {
        swap(index/2,index);//交换
        index = index/2;
    }
}

既然利用上浮操作建堆已经搞懂啦，那么我们再来了解一下，利用下沉操作建堆吧，也很容易理解。

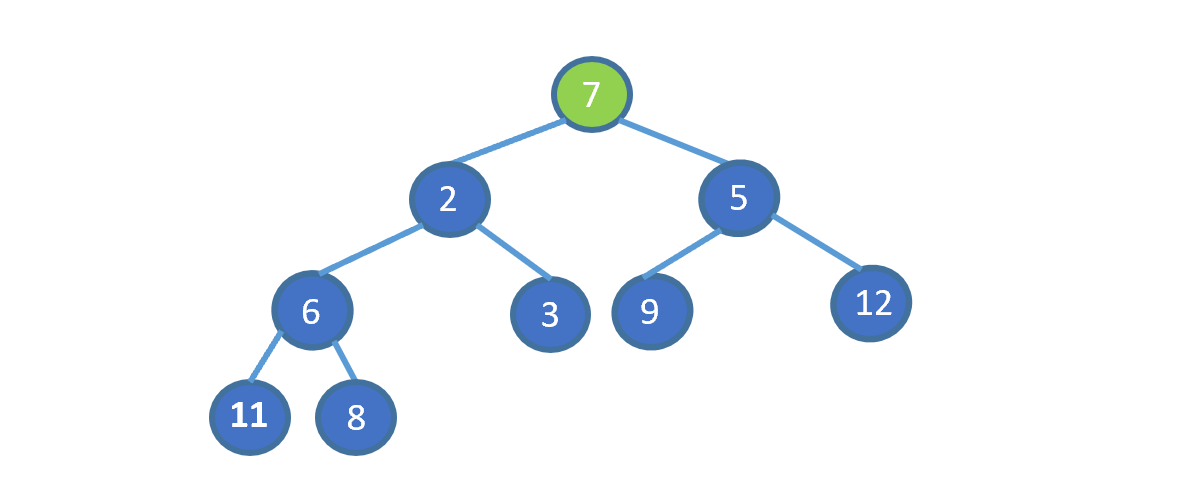
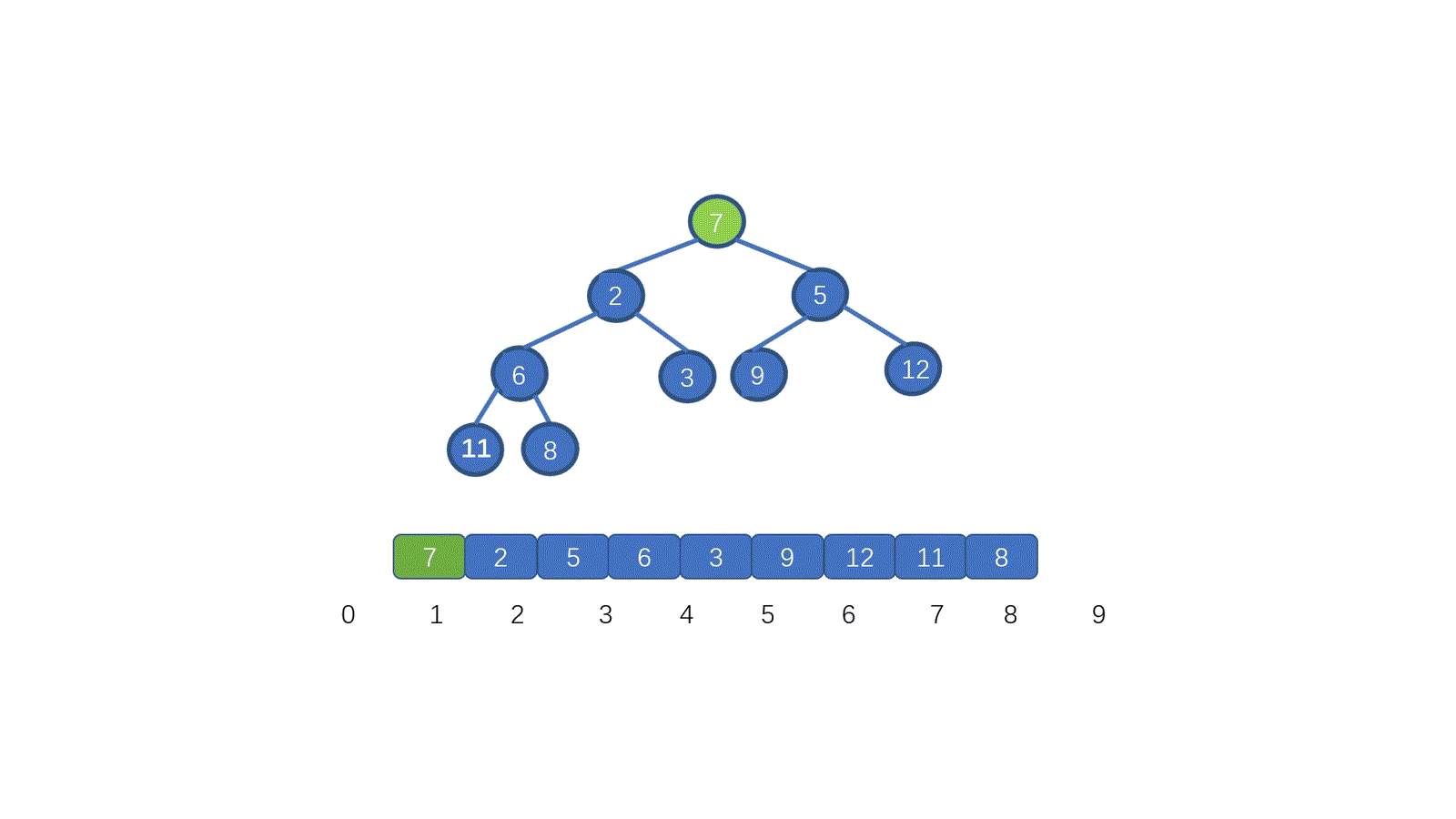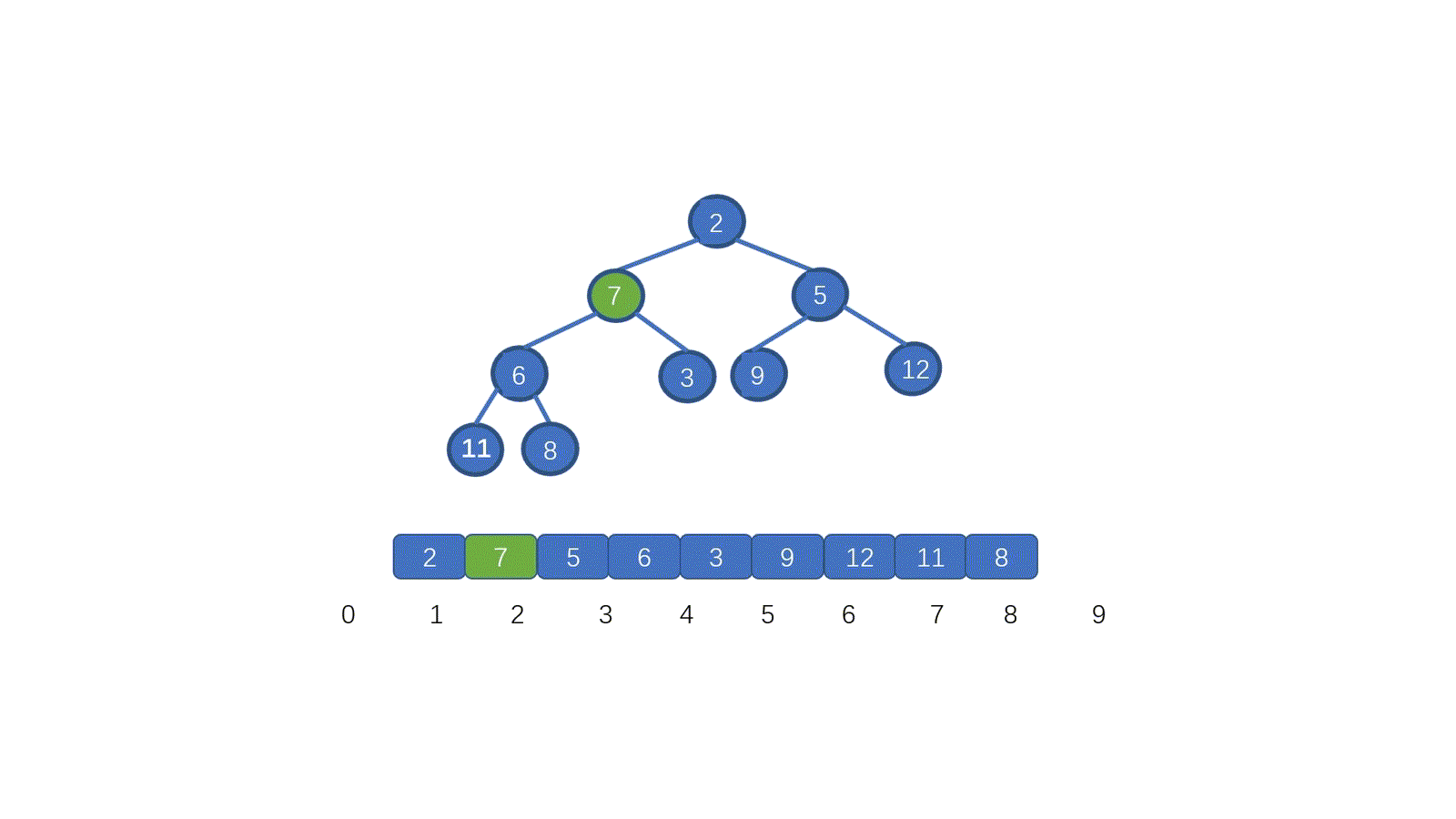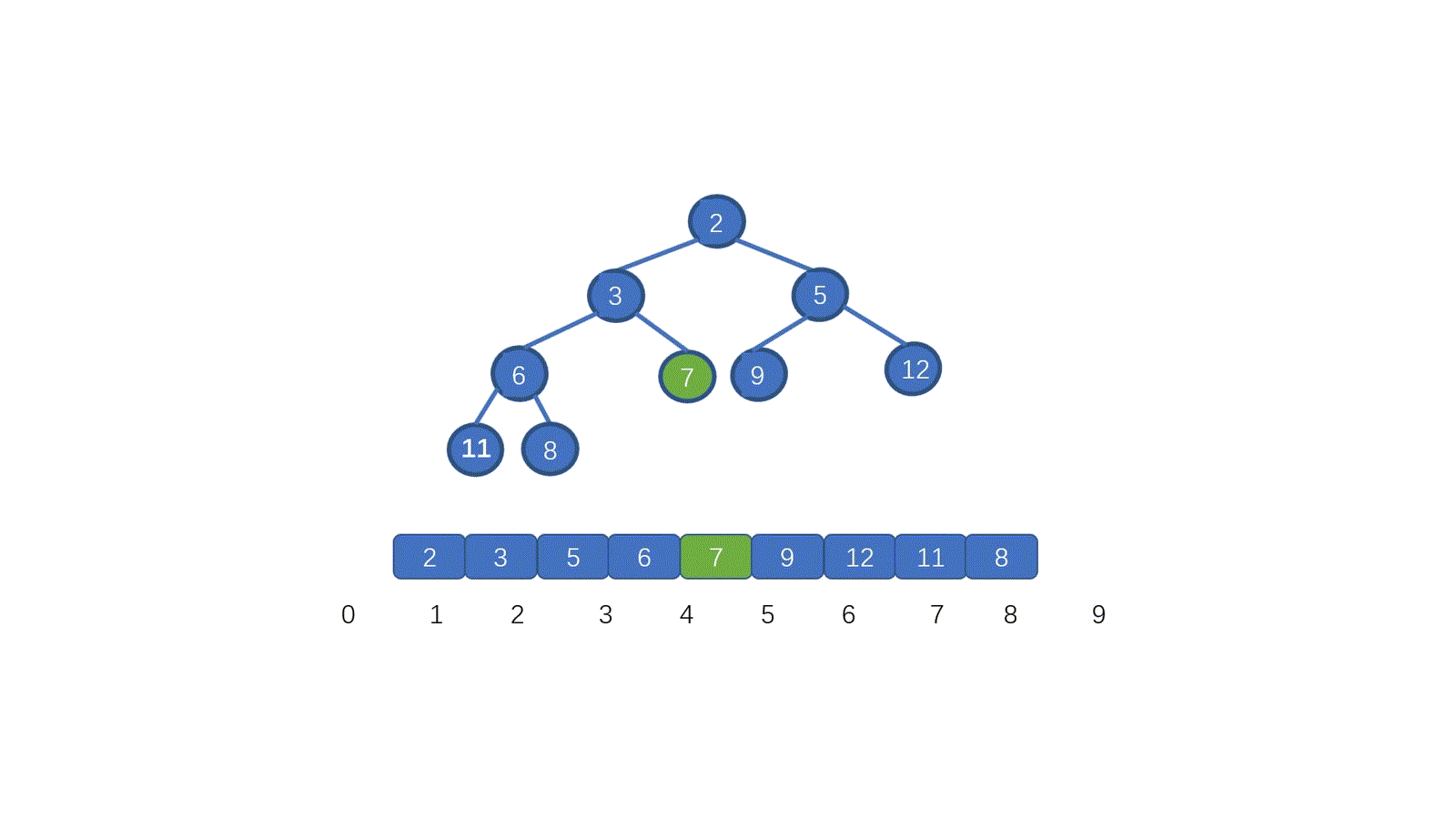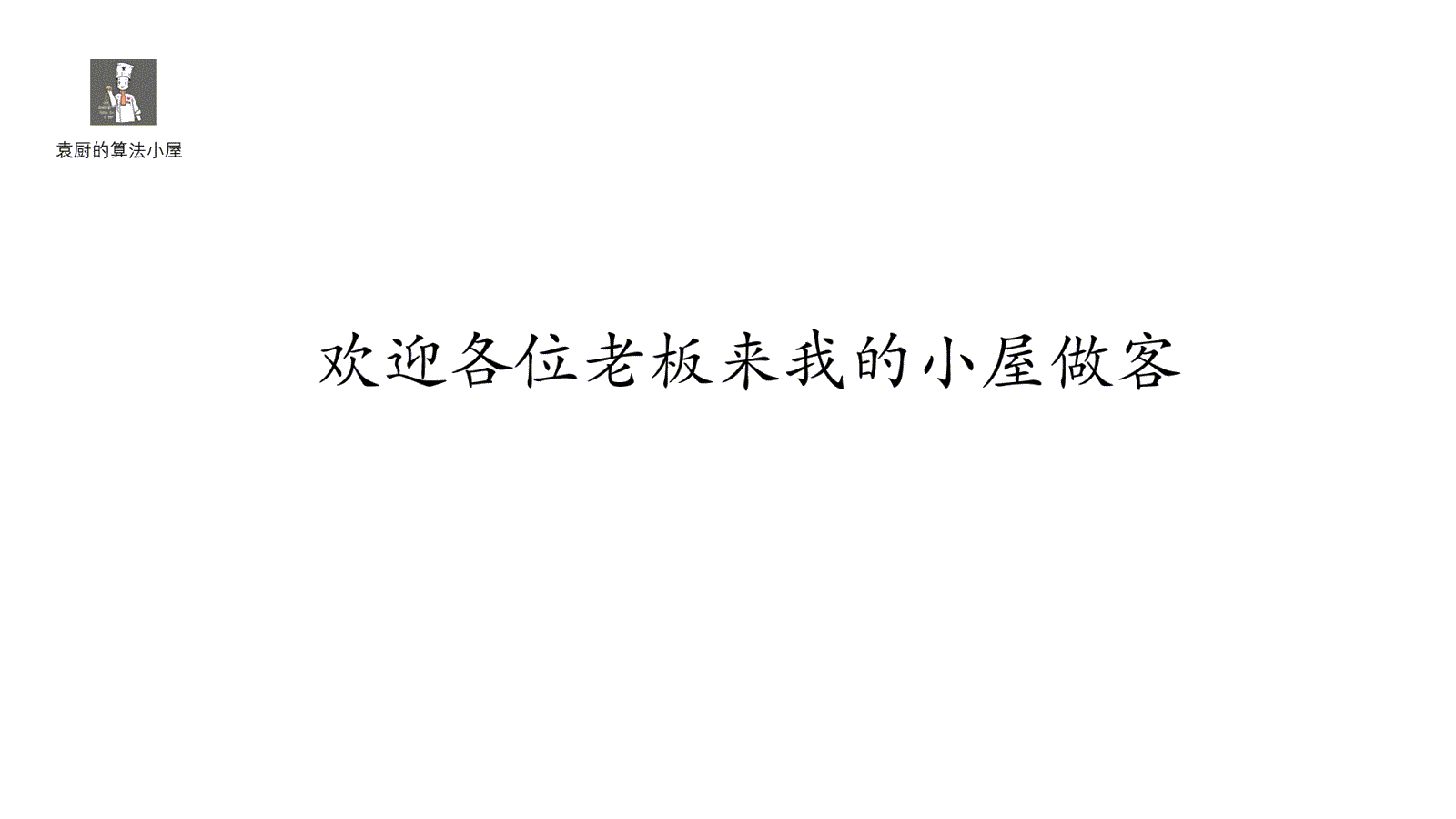
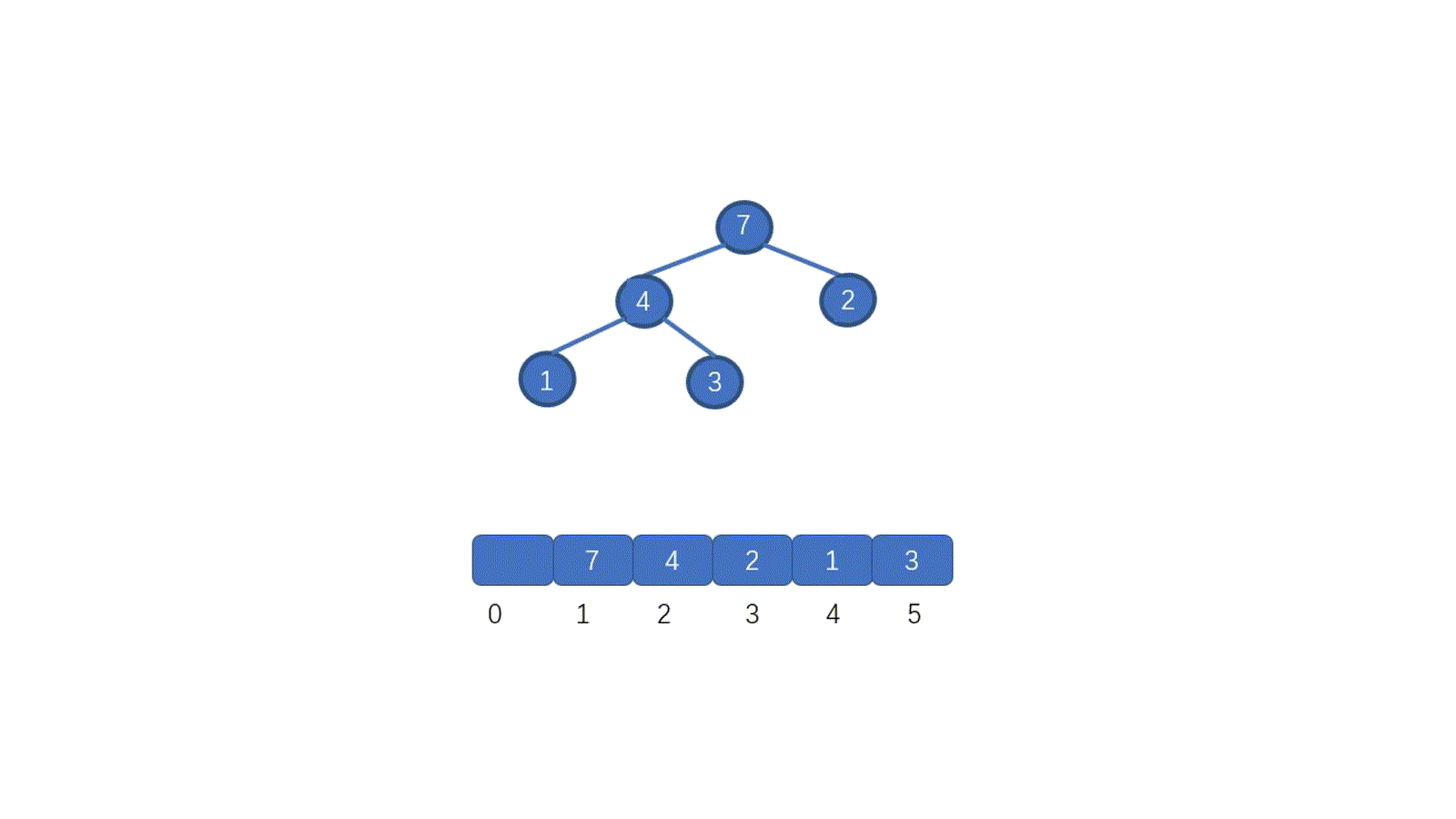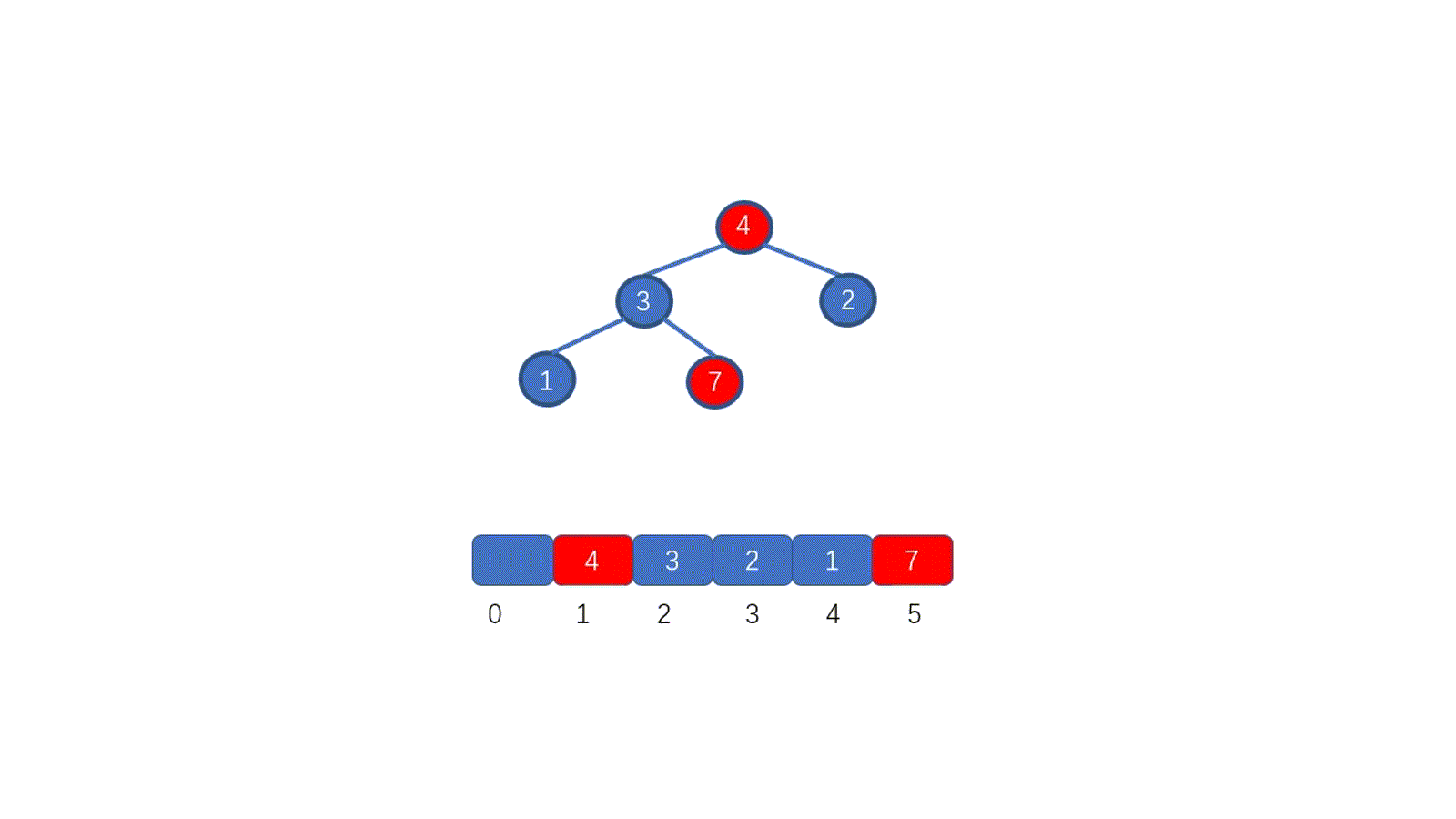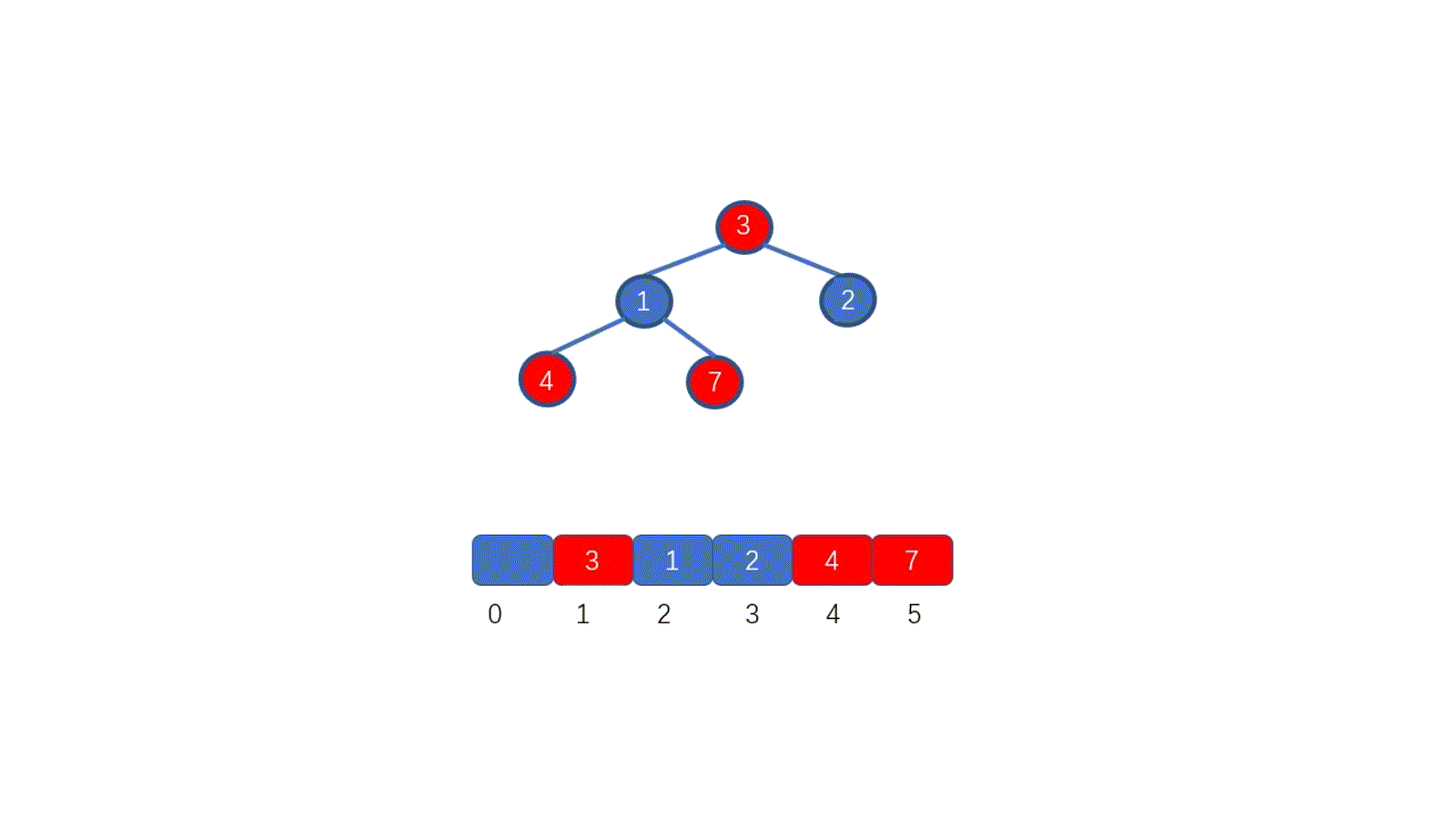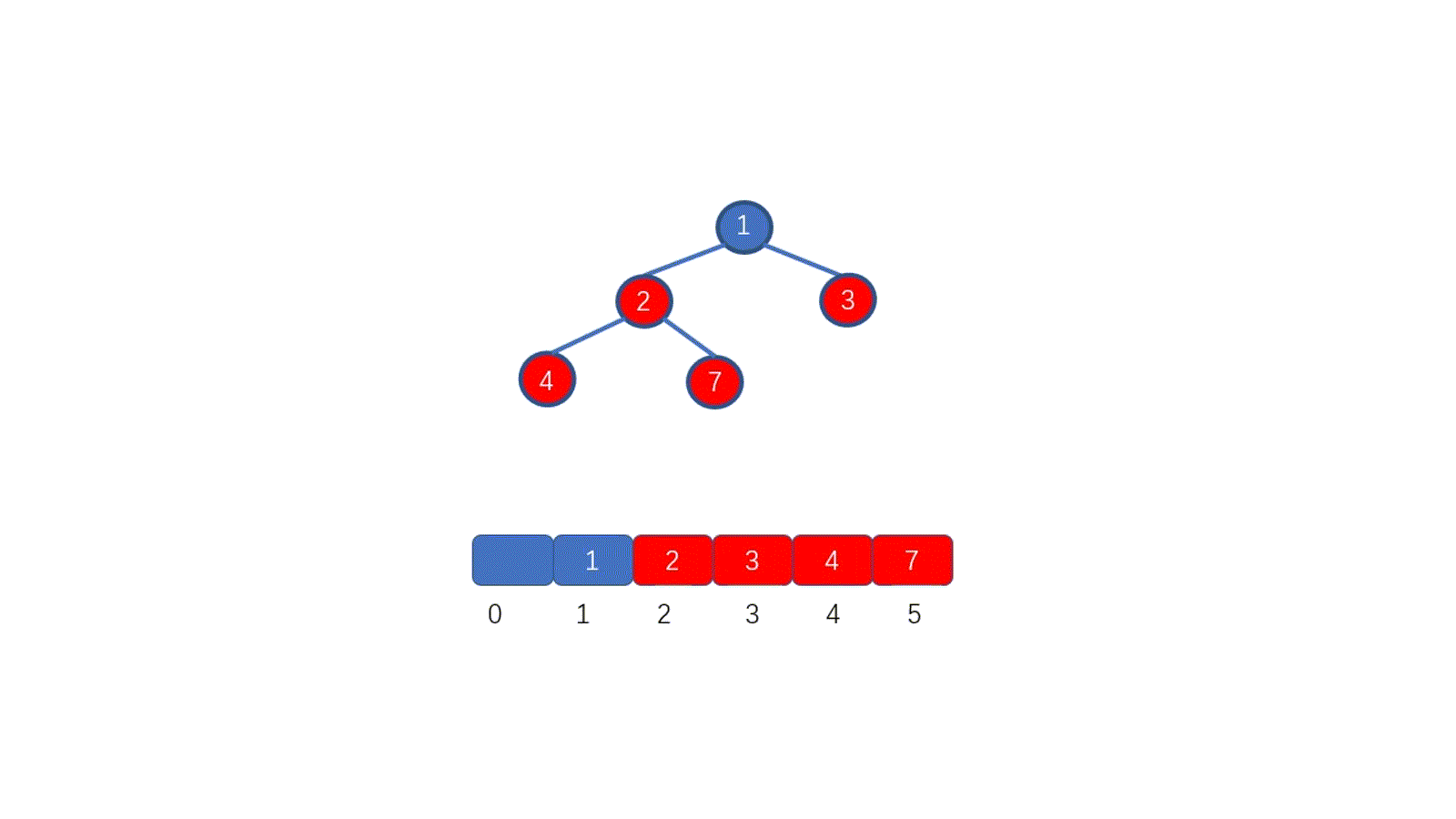
给我们一个无序数组（不满足堆的要求），见下图

我们发现，7 位于堆顶，但是此时并不满足小顶堆的要求，我们需要把 7 放到属于它的位置，我们应该怎么做呢？

废话不多说，我们先来看视频模拟，看完保准可以懂

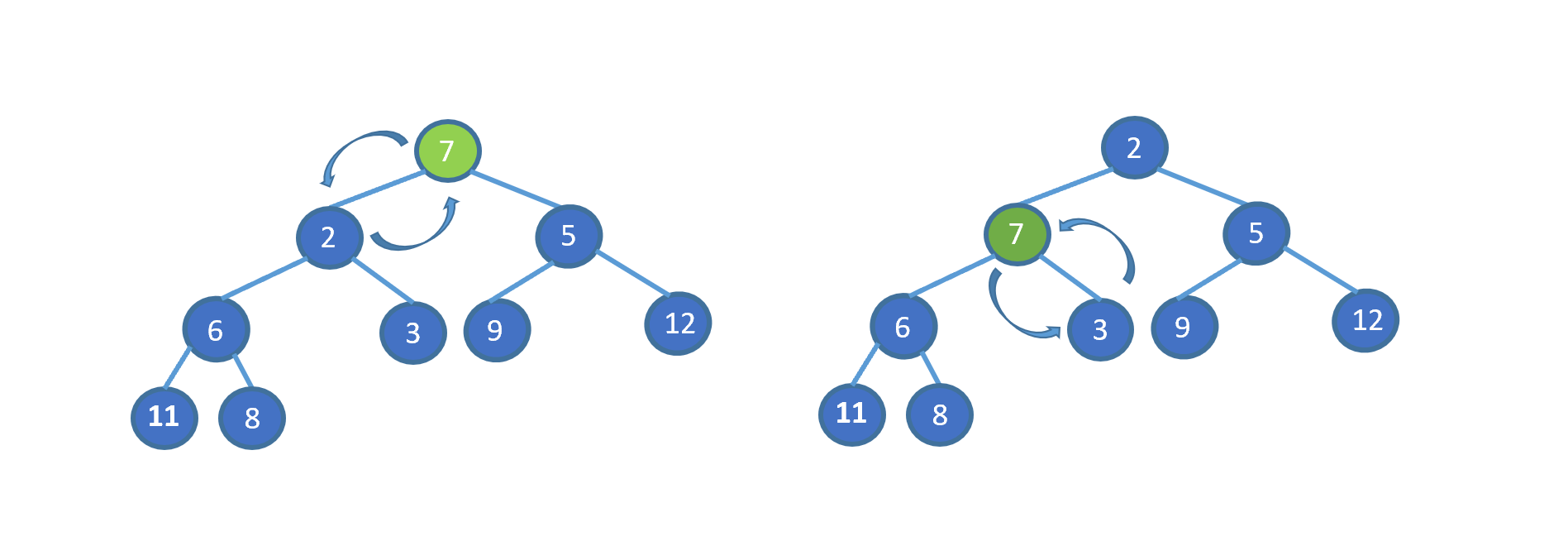
看完视频是不是懂个大概了，但是不知道大家有没有注意到这个地方。为什么 7 第一次与其左孩子节点 2 交换，第二次与右孩子节点 3 交换。见下图

其实很容易理解，我们需要与孩子节点中最小的那个交换，因为我们需要交换后，父节点小于两个孩子节点，如果我们第一步，7 与 5 进行交换的话，则同样不能满足小顶堆。

那我们怎么判断节点找到属于它的位置了呢？主要有两个情况

• 待下沉元素小于（大于）两个子节点，此时符合堆的规则，无序下沉，例如上图中的 6
• 下沉为叶子节点，此时没有子节点，例如 7 下沉到最后变成了叶子节点。

我们将上面的操作称之为下沉操作。

这时我们又有疑问了，下沉操作我懂了，但是这跟建堆有个锤子关系啊！

不要急，我们继续来看视频，这次我们通过下沉操作建个大顶堆。

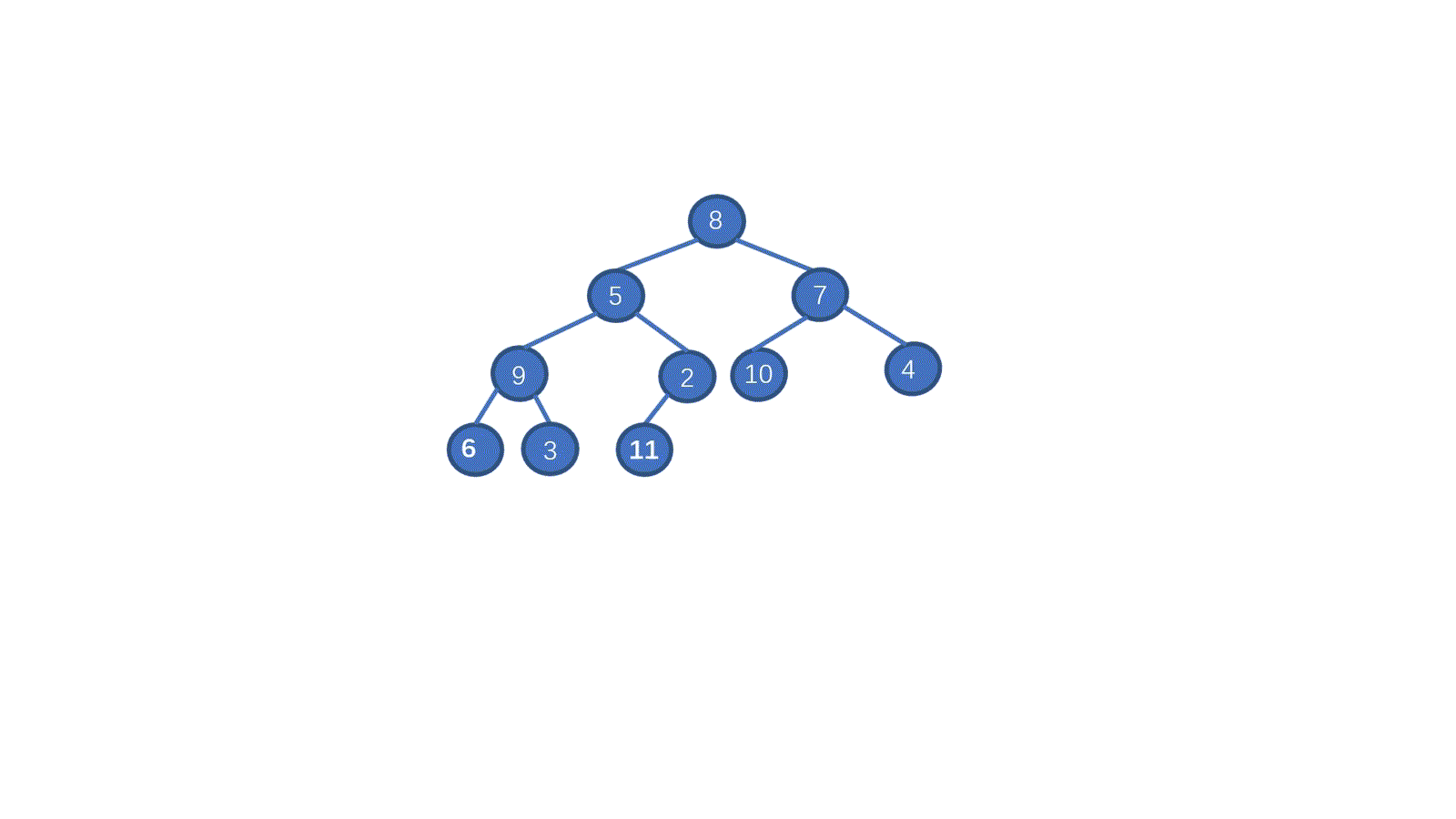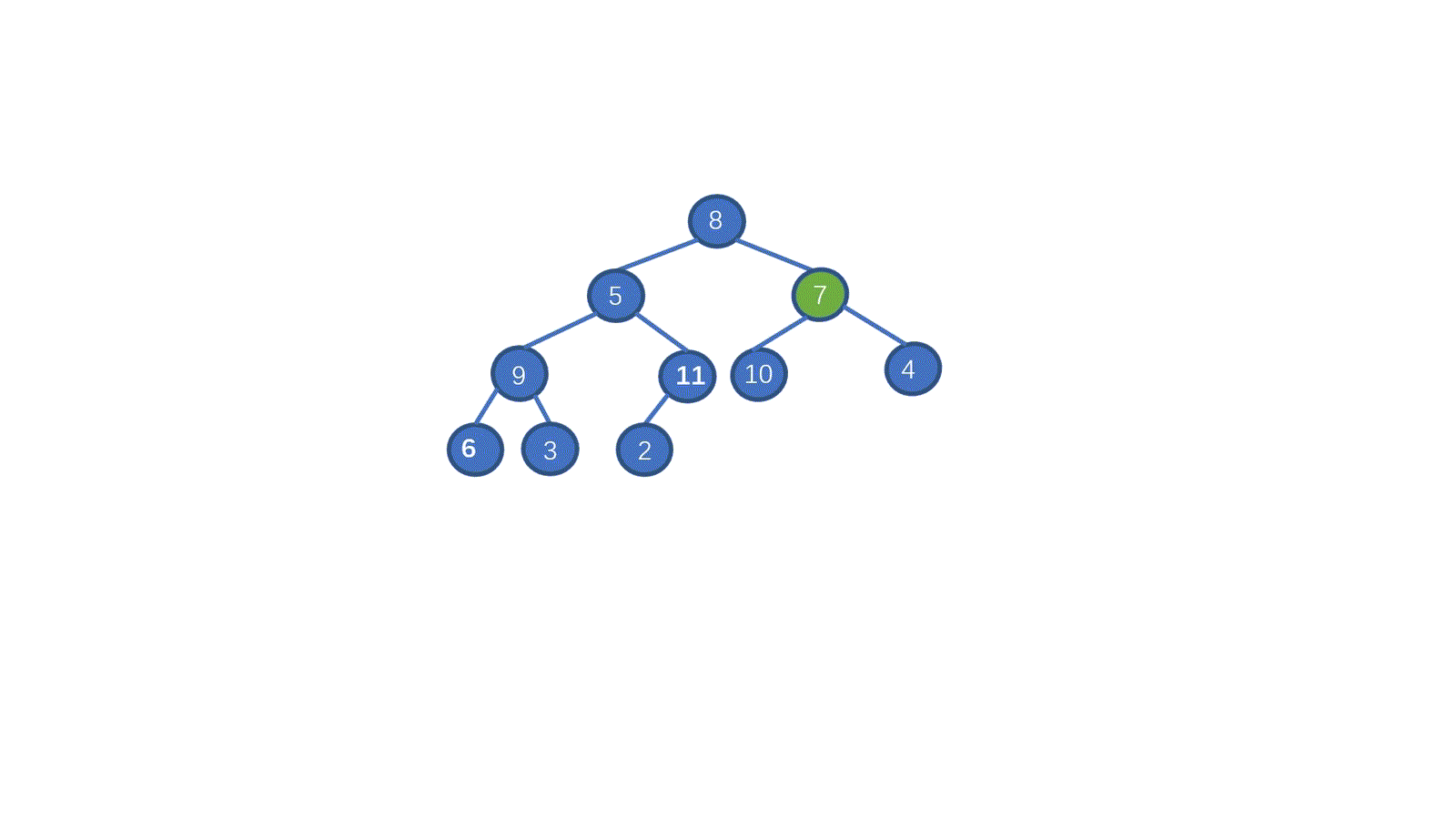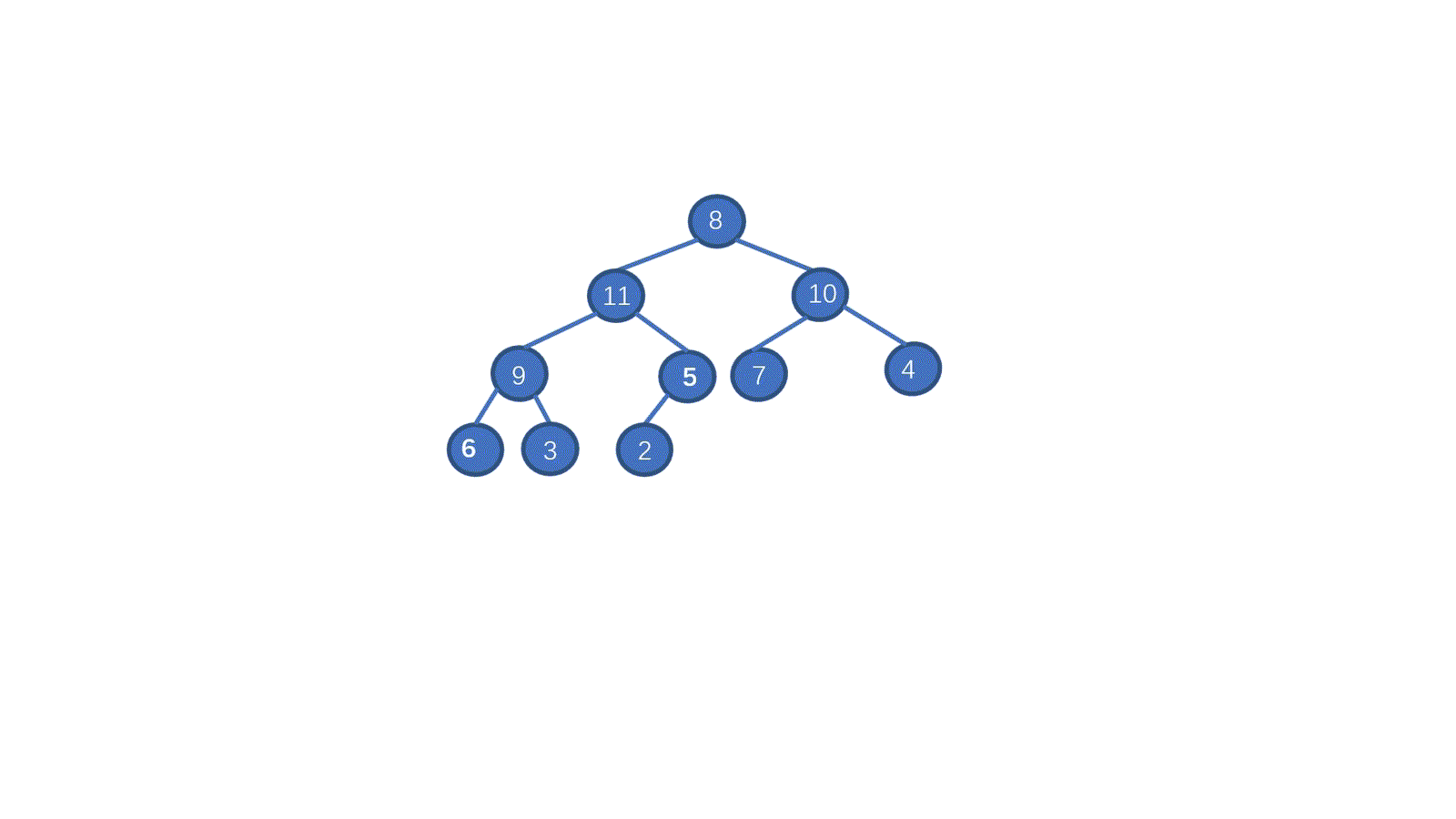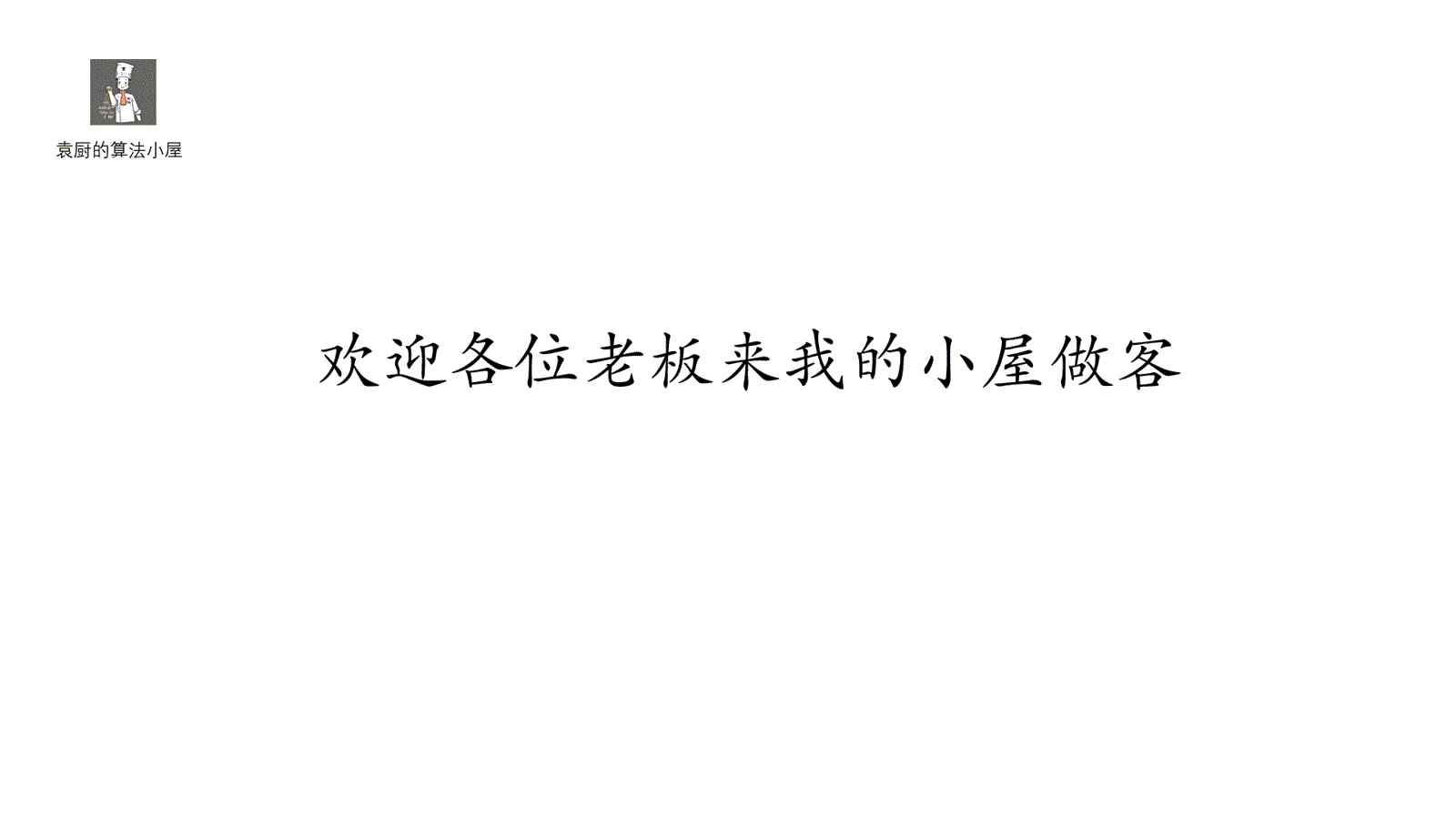
初始数组 [8,5,7,9,2,10,1,4,6,3]

我们一起来拆解一下视频，我们只需要从最后一个非叶子节点开始，依次执行下沉操作。执行完毕后我们就能够完成堆化。是不是一下就懂了呀。

好啦我们一起看哈下沉操作的代码吧。

public void sink (int[] nums, int index,int len) {
        while (true) {
            //获取子节点
            int j = 2 * index;
            if (j < len-1 && nums[j] < nums[j+1]) {
                j++;
            }
            //交换操作，父节点下沉，与最大的孩子节点交换
            if (j < len && nums[index] < nums[j]) {
                swap(nums,index,j);
            } else {
                break;
            } 
            //继续下沉
            index = j;
        }
    }

好啦，两种建堆方式我们都已经了解啦，那么我们如何进行排序呢？

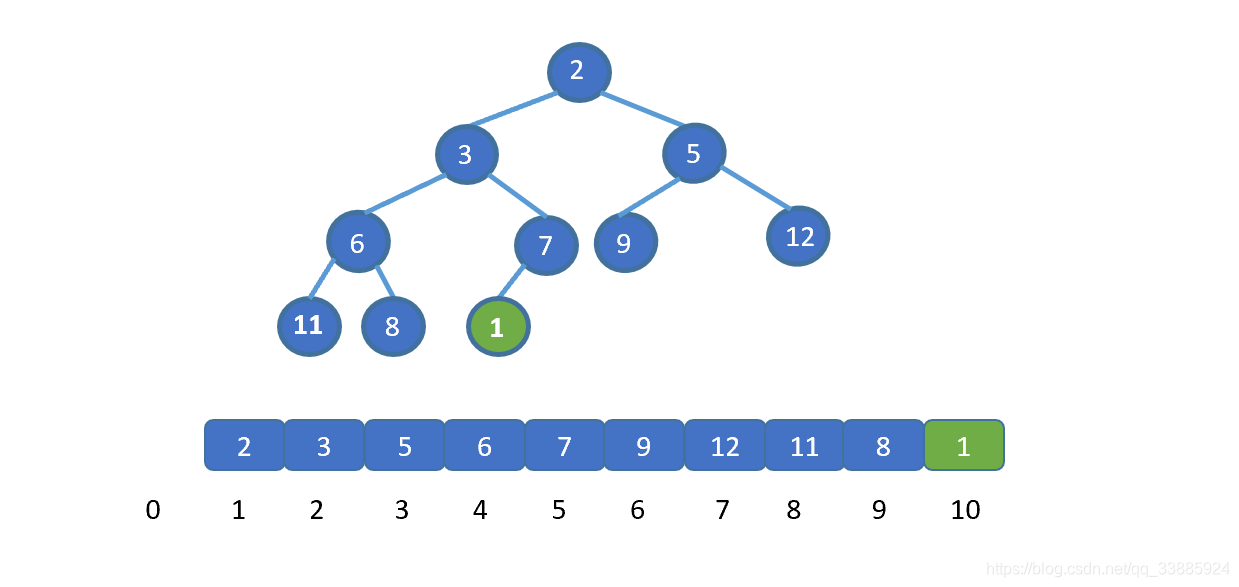
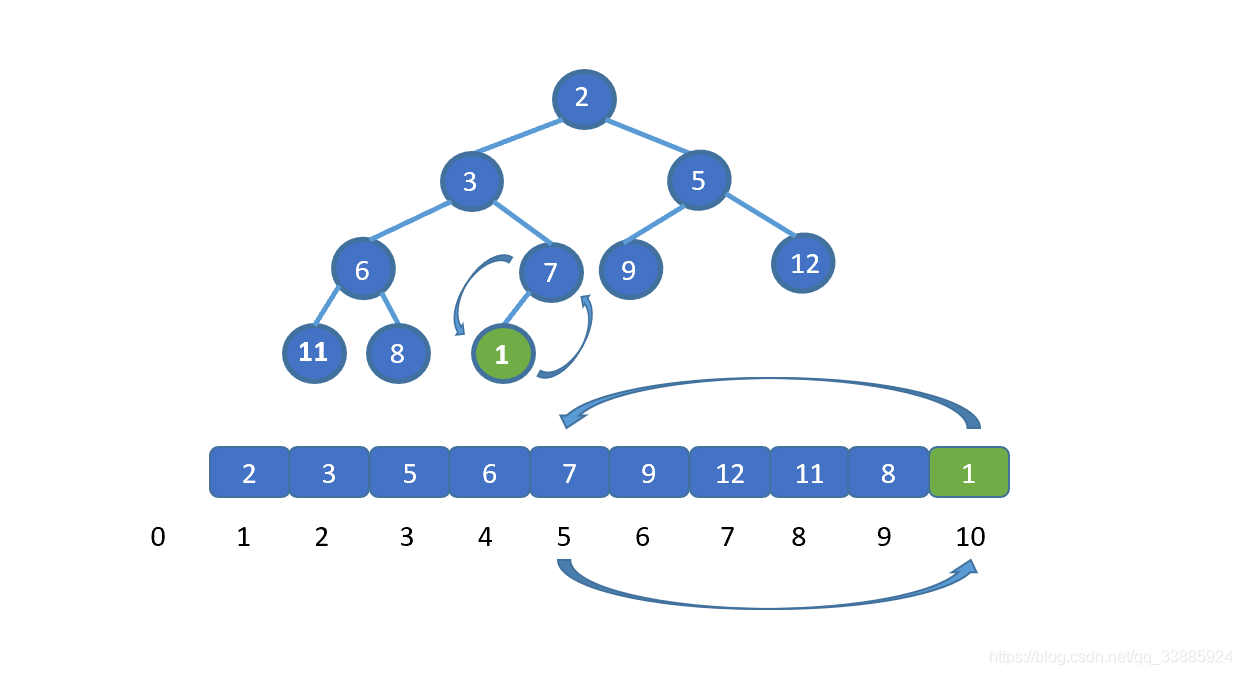
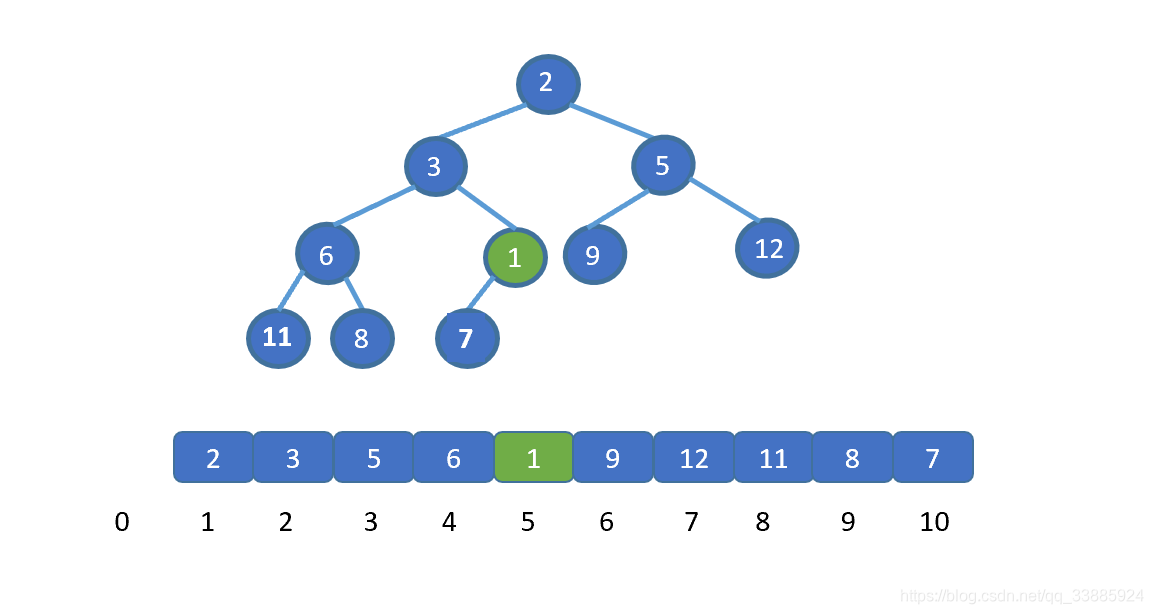
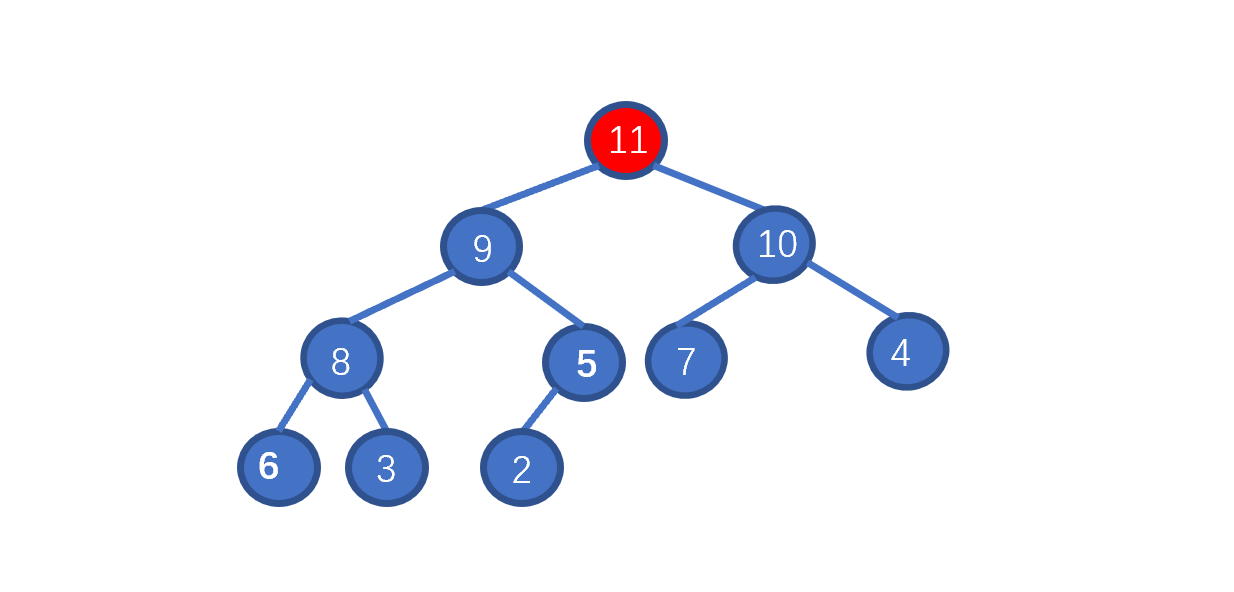
了解排序之前我们先来，看一下如何删除堆顶元素，我们需要保证的是，删除堆顶元素后，其他元素仍能满足堆的要求，我们思考一下如何实现呢？见下图

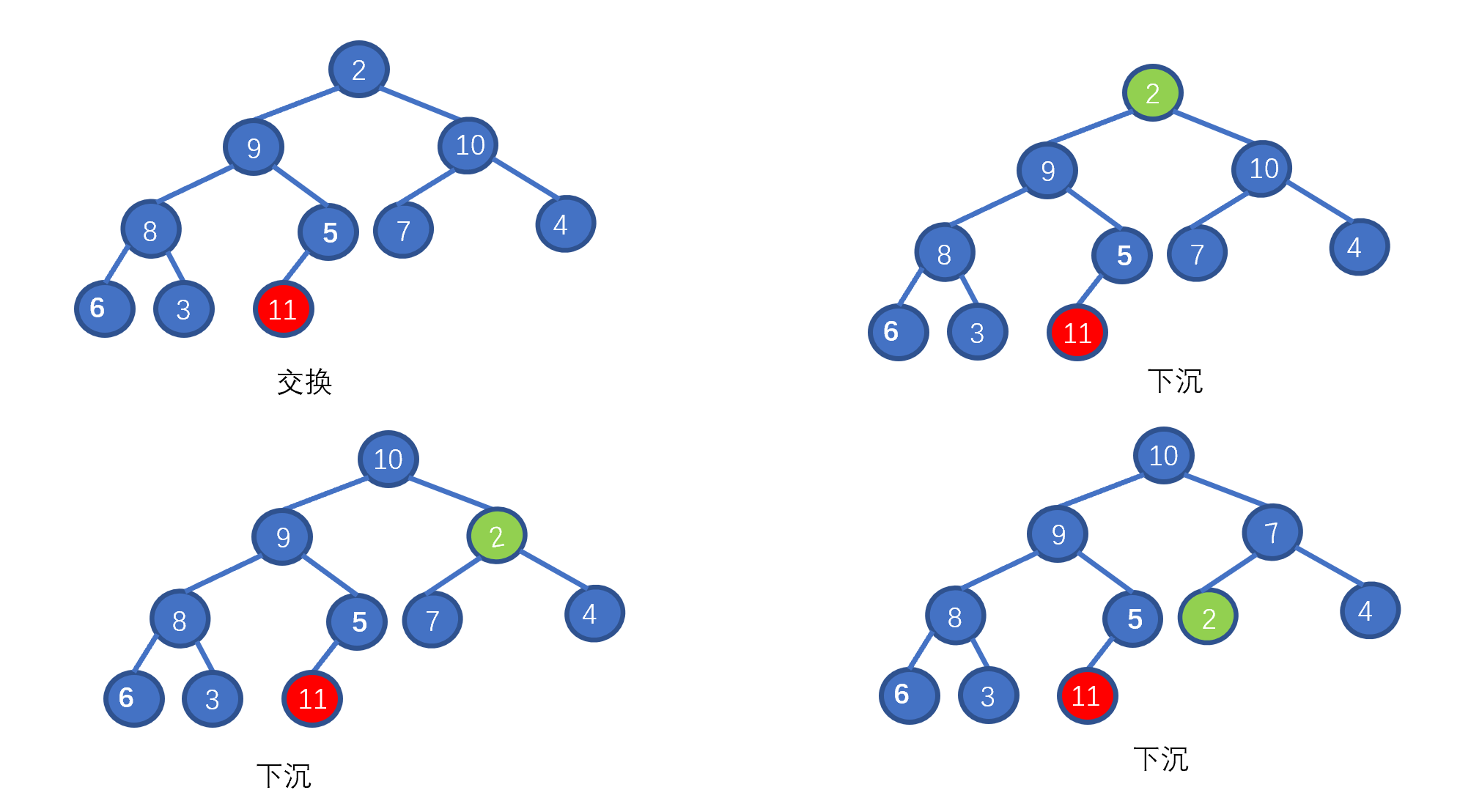
假设我们想要去除堆顶的 11 ，那我们则需要将其与堆的最后一个节点交换也就是 2 ，2然后再执行下沉操作，执行完毕后仍能满足堆的要求，见下图

好啦，其实你已经学会如何排序啦！你不信？那我给你放视频

好啦，大家是不是已经搞懂啦，下面我们总结一下堆排序的具体执行过程

1.建堆，通过下沉操作建堆效率更高，具体过程是，找到最后一个非叶子节点，然后从后往前遍历执行下沉操作。

2.排序，将堆顶元素（代表最大元素）与最后一个元素交换，然后新的堆顶元素进行下沉操作，遍历执行上诉操作，则可以完成排序。

好啦，下面我们一起看代码吧

class Solution {
    public int[] sortArray(int[] nums) {

        int len = nums.length;
        int[] a = new int[len + 1];

        for (int i = 0; i < nums.length; ++i) {
            a[i+1] = nums[i];
        }          
        //下沉建堆
        for (int i = len/2; i >= 1; --i) {
            sink(a,i,len);
        }

        int k = len;
        //排序
        while (k > 1) {
            swap(a,1,k--);
            sink(a,1,k);
        }
        for (int i = 1; i < len+1; ++i) {
            nums[i-1] = a[i];
        }
        return nums;
    }
    public void sink (int[] nums, int k,int end) {
        //下沉
        while (2 * k <= end) {
            int j = 2 * k;
            //找出子节点中最大或最小的那个
            if (j + 1 <= end && nums[j + 1] > nums[j]) {
                j++;
            }
            if (nums[j] > nums[k]) {
                swap(nums, j, k);
            } else {
                break;
            }
            k = j;
        }
    }
    public void swap (int nums[], int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    
}

好啦，堆排序我们就到这里啦，是不是搞定啦，总的来说堆排序比其他排序算法稍微难理解一些，重点就是建堆，而且应用比较广泛，大家记得打卡呀。

好啦，我们再来分析一下堆排序的时间复杂度、空间复杂度以及稳定性。

堆排序时间复杂度分析

因为我们建堆的时间复杂度为 O(n），排序过程的时间复杂度为 O(nlogn),所以总的空间复杂度为 O(nlogn)

堆排序空间复杂度分析

这里需要注意，我们上面的描述过程中，为了更直观的描述，空出数组的第一位，这样我们就可以通过 i * 2 和 i * 2+1 来求得左孩子节点和右孩子节点 。我们也可以根据 i * 2 + 1 和 i * 2 + 2 来获取孩子节点，这样则不需要临时数组来处理原数组，将所有元素后移一位，所以堆排序的空间复杂度为 O(1),是原地排序算法。

堆排序稳定性分析

堆排序不是稳定的排序算法，在排序的过程，我们会将堆的最后一个节点跟堆顶节点交换，改变相同元素的原始相对位置。

最后我们来比较一下我们快速排序和堆排序

1.对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的。这样对 CPU 缓存是不友好的

2.相同的的数据，排序过程中，堆排序的数据交换次数要多于快速排序。

所以上面两条也就说明了在实际开发中，堆排序的性能不如快速排序性能好。

好啦，今天的内容就到这里啦，咱们下期见。