mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-20 02:53:39 +00:00
135 lines
5.2 KiB
Java
135 lines
5.2 KiB
Java
> 如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 **[tan45du_one](https://raw.githubusercontent.com/tan45du/tan45du.github.io/master/个人微信.15egrcgqd94w.jpg)** ,备注 github + 题目 + 问题 向我反馈
|
||
>
|
||
> 感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
|
||
>
|
||
> 另外希望手机阅读的同学可以来我的 <u>[**公众号:袁厨的算法小屋**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u> 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击<u>[**刷题小队**](https://raw.githubusercontent.com/tan45du/test/master/微信图片_20210320152235.2pthdebvh1c0.png)</u>进入。
|
||
|
||
#### [974. 和可被 K 整除的子数组](https://leetcode-cn.com/problems/subarray-sums-divisible-by-k/)
|
||
|
||
**题目描述**
|
||
|
||
> 给定一个整数数组 A,返回其中元素之和可被 K 整除的(连续、非空)子数组的数目。
|
||
|
||
**示例:**
|
||
|
||
> 输入:A = [4,5,0,-2,-3,1], K = 5
|
||
> 输出:7
|
||
|
||
**解释:**
|
||
|
||
> 有 7 个子数组满足其元素之和可被 K = 5 整除:
|
||
> [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
|
||
|
||
**前缀和+HashMap**
|
||
|
||
**解析**
|
||
|
||
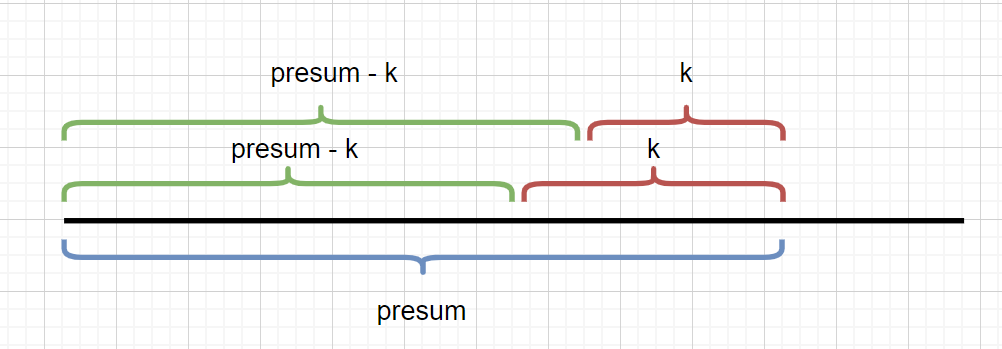
我们在该文的第一题 **和为K的子数组 **中,我们需要求出满足条件的区间,见下图
|
||
|
||
|
||
|
||
我们需要找到满足,和为 K 的区间。我们此时 presum 是已知的,k 也是已知的,我们只需要找到 presum - k区间的个数,就能得到 k 的区间个数。但是我们在当前题目中应该怎么做呢?见下图。
|
||
|
||

|
||
|
||
我们在之前的例子中说到,presum[j+1] - presum[i] 可以得到 nums[i] + nums[i+1]+.... nums[j],也就是[i,j]区间的和。
|
||
|
||
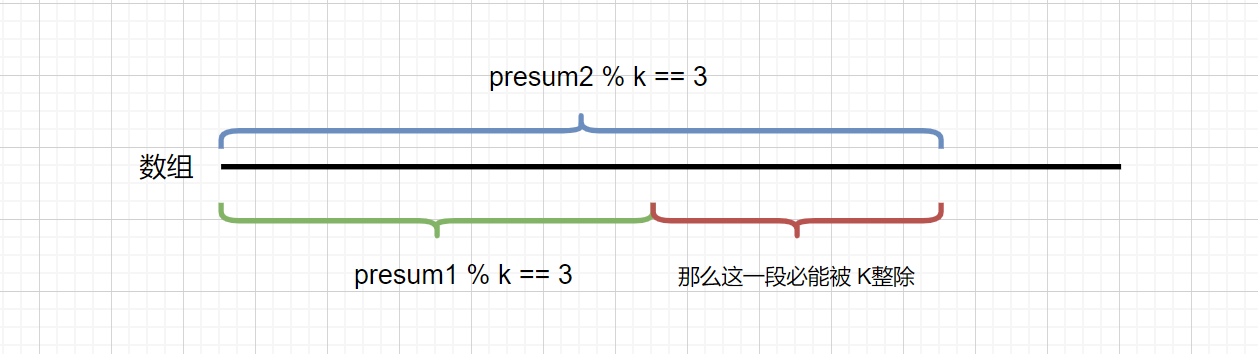
那么我们想要判断区间 [i,j] 的和是否能整除 K,也就是上图中紫色那一段是否能整除 K,那么我们只需判断
|
||
|
||
(presum[j+1] - presum[i] ) % k 是否等于 0 即可,
|
||
|
||
我们假设 (presum[j+1] - presum[i] ) % k == 0;则
|
||
|
||
presum[j+1] % k - presum[i] % k == 0;
|
||
|
||
presum[j +1] % k = presum[i] % k ;
|
||
|
||
我们 presum[j +1] % k 的值 key 是已知的,则是当前的 presum 和 k 的关系,我们只需要知道之前的前缀区间里含有相同余数 (key)的个数。则能够知道当前能够整除 K 的区间个数。见下图
|
||
|
||
|
||
|
||
|
||
|
||
**题目代码**
|
||
|
||
```java
|
||
class Solution {
|
||
public int subarraysDivByK(int[] A, int K) {
|
||
HashMap<Integer,Integer> map = new HashMap<>();
|
||
map.put(0,1);
|
||
int presum = 0;
|
||
int count = 0;
|
||
for (int x : A) {
|
||
presum += x;
|
||
//当前 presum 与 K的关系,余数是几,当被除数为负数时取模结果为负数,需要纠正
|
||
int key = (presum % K + K) % K;
|
||
//查询哈希表获取之前key也就是余数的次数
|
||
if (map.containsKey(key)) {
|
||
count += map.get(key);
|
||
}
|
||
//存入哈希表当前key,也就是余数
|
||
map.put(key,map.getOrDefault(key,0)+1);
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
我们看到上面代码中有一段代码是这样的
|
||
|
||
```java
|
||
int key = (presum % K + K) % K;
|
||
```
|
||
|
||
这是为什么呢?不能直接用 presum % k 吗?
|
||
|
||
这是因为当我们 presum 为负数时,需要对其纠正。纠正前(-1) %2 = (-1),纠正之后 ( (-1) % 2 + 2) % 2=1 保存在哈希表中的则为 1.则不会漏掉部分情况,例如输入为 [-1,2,9],K = 2如果不对其纠正则会漏掉区间 [2] 此时 2 % 2 = 0,符合条件,但是不会被计数。
|
||
|
||
那么这个题目我们可不可以用数组,代替 map 呢?当然也是可以的,因为此时我们的哈希表存的是余数,余数最大也只不过是 K-1所以我们可以用固定长度 K 的数组来模拟哈希表。
|
||
|
||
Java Code:
|
||
|
||
```java
|
||
class Solution {
|
||
public int subarraysDivByK(int[] A, int K) {
|
||
int[] map = new int[K];
|
||
map[0] = 1;
|
||
int len = A.length;
|
||
int presum = 0;
|
||
int count = 0;
|
||
for (int i = 0; i < len; ++i) {
|
||
presum += A[i];
|
||
//求key
|
||
int key = (presum % K + K) % K;
|
||
//count添加次数,并将当前的map[key]++;
|
||
count += map[key]++;
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
C++ Code:
|
||
|
||
```cpp
|
||
class Solution {
|
||
public:
|
||
int subarraysDivByK(vector<int>& A, int K) {
|
||
vector <int> map (K, 0);
|
||
int len = A.size();
|
||
int count = 0;
|
||
int presum = 0;
|
||
map[0] = 1;
|
||
for (int i = 0; i < len; ++i) {
|
||
presum += A[i];
|
||
//求key
|
||
int key = (presum % K + K) % K;
|
||
//count添加次数,并将当前的map[key]++;
|
||
count += (map[key]++);
|
||
}
|
||
return count;
|
||
}
|
||
};
|
||
```
|
||
|