gopl-zh.github.com

4.9 KiB

Raw Blame History

3.2. 浮點數

Go语言提供了两种精度的浮点数, float32 和 float64. 它们的算术规范由 IEEE754 国际标准定义, 该浮点数规范被所有现代的CPU支持.

这些数值类型的范围可以从很微小到很巨大. 浮点数的范围极限值可以在 matn 包找到. 常量 math.MaxFloat32 表示 float32 能表示的最大数值, 大约是 3.4e38, 对应的 math.MaxFloat64 常量大约是 1.8e308. 它们能表示的最小值近似分别是1.4e-45 和 4.9e-324.

一个 float32 类型的浮点数可以提供大约6个十进制数的精度, 而 float64 则可以提供约 15个十进制数精度; 通常应该优先使用 float64 类型, 因为 float32 类型的累计计算误差很容易扩散, 并且 float32 能精度表示的正整数并不是很大:

var f float32 = 16777216 // 1 << 24
fmt.Println(f == f+1)    // "true"!

浮点数的字面值可以直接写小数部分, 想这样:

const e = 2.71828 // (approximately)

小数点前面或后面的数字都可能被省略(例如 .707 或 1.). 很小或很大的数最好用科学计数法书写, 通过e或E来指定指数部分:

const Avogadro = 6.02214129e23 
const Planck   = 6.62606957e-34

用 Printf 函数的 %g 参数打印浮点数, 将采用紧凑的表示形式打印, 并提供足够的精度, 但是对应表格的数据, 使用 %e (带指数) 或 %f 的形式打印可能更合适. 所有的这三个打印形式都可以指定打印的宽度和控制打印精度.

for x := 0; x < 8; x++ {
	fmt.Printf("x = %d e^x = %8.3f\n", x, math.Exp(float64(x)))
}

上面代码打印e的幂, 打印精度是小数点后三个小数精度和8个字符宽度:

x = 0       e^x =    1.000
x = 1       e^x =    2.718
x = 2       e^x =    7.389
x = 3       e^x =   20.086
x = 4       e^x =   54.598
x = 5       e^x =  148.413
x = 6       e^x =  403.429
x = 7       e^x = 1096.633

math 包中除了提供大量常用的数学函数外, 还提供了IEEE754标准中特殊数值的创建和测试: 正无穷大和负无穷大, 分别用于表示太大溢出的数字和除零的结果; 还有 NaN 非数, 一般用于表示无效的除法操作结果 0/0 或 Sqrt(-1).

var z float64
fmt.Println(z, -z, 1/z, -1/z, z/z) // "0 -0 +Inf -Inf NaN"

函数 math.IsNaN 用于测试一个数是否是非数 NaN, math.NaN 则返回非数对应的值. 虽然可以用 math.NaN 来表示一个非法的结果, 但是测试一个结果是否是非数 NaN 则是充满风险, 因为 NaN 和任何数都是不相等的:

nan := math.NaN()
fmt.Println(nan == nan, nan < nan, nan > nan) // "false false false"

如果一个函数返回的浮点数结果可能失败, 最好的做法是用单独的标志报告失败, 像这样:

func compute() (value float64, ok bool) {
	// ...
	if failed {
		return 0, false
	}
	return result, true
}

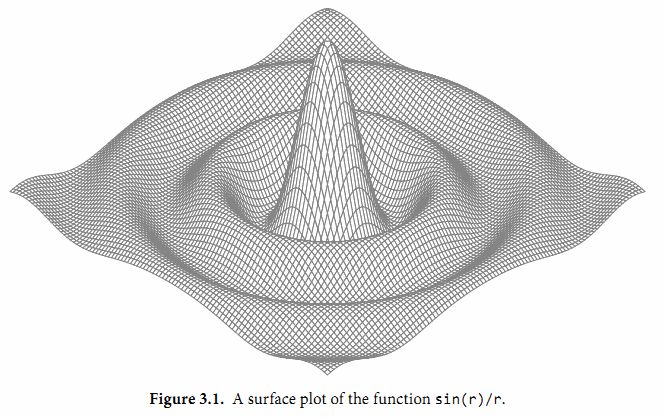
接下来的程序演示了浮点计算图形. 它是带有两个参数的 z = f(x, y) 函数的三维形式, 使用了可缩放矢量图形(SVG)格式输出, 一个用于矢量线绘制的XML标准. 图3.1显示了 sin(r)/r 函数的输出图形, 其中 r 是 sqrt(xx+yy).

gopl.io/ch3/surface
// Surface computes an SVG rendering of a 3-D surface function.
package main

import (
	"fmt"
	"math"
)

const (
	width, height = 600, 320            // canvas size in pixels
	cells         = 100                 // number of grid cells
	xyrange       = 30.0                // axis ranges (-xyrange..+xyrange)
	xyscale       = width / 2 / xyrange // pixels per x or y unit
	zscale        = height * 0.4        // pixels per z unit
	angle         = math.Pi / 6         // angle of x, y axes (=30°)
)

var sin30, cos30 = math.Sin(angle), math.Cos(angle) // sin(30°), cos(30°)

func main() {
	fmt.Printf("<svg xmlns='http://www.w3.org/2000/svg' "+
		"style='stroke: grey; fill: white; stroke-width: 0.7' "+
		"width='%d' height='%d'>", width, height)
	for i := 0; i < cells; i++ {
		for j := 0; j < cells; j++ {
			ax, ay := corner(i+1, j)
			bx, by := corner(i, j)
			cx, cy := corner(i, j+1)
			dx, dy := corner(i+1, j+1)
			fmt.Printf("<polygon points='%g,%g %g,%g %g,%g %g,%g'/>\n",
				ax, ay, bx, by, cx, cy, dx, dy)
		}
	}
	fmt.Println("</svg>")
}

func corner(i, j int) (float64, float64) {
	// Find point (x,y) at corner of cell (i,j).
	x := xyrange * (float64(i)/cells - 0.5)
	y := xyrange * (float64(j)/cells - 0.5)

	// Compute surface height z.
	z := f(x, y)

	// Project (x,y,z) isometrically onto 2-D SVG canvas (sx,sy).
	sx := width/2 + (x-y)*cos30*xyscale
	sy := height/2 + (x+y)*sin30*xyscale - z*zscale
	return sx, sy
}

func f(x, y float64) float64 {
	r := math.Hypot(x, y) // distance from (0,0)
	return math.Sin(r) / r
}

要注意的是 corner 返回了两个结果, 对应 corner 的坐标参数.

TODO

4.9 KiB Raw Blame History

3.2. 浮點數

4.9 KiB

Raw Blame History