7.1 KiB
3.2. 浮點數
Go语言提供了两种精度的浮点数, float32 和 float64. 它们的算术规范由 IEEE754 国际标准定义, 该浮点数规范被所有现代的CPU支持.
这些数值类型的范围可以从很微小到很巨大. 浮点数的范围极限值可以在 matn 包找到. 常量 math.MaxFloat32 表示 float32 能表示的最大数值, 大约是 3.4e38, 对应的 math.MaxFloat64 常量大约是 1.8e308. 它们能表示的最小值近似分别是1.4e-45 和 4.9e-324.
一个 float32 类型的浮点数可以提供大约6个十进制数的精度, 而 float64 则可以提供约 15个十进制数精度; 通常应该优先使用 float64 类型, 因为 float32 类型的累计计算误差很容易扩散, 并且 float32 能精度表示的正整数并不是很大:
var f float32 = 16777216 // 1 << 24
fmt.Println(f == f+1) // "true"!
浮点数的字面值可以直接写小数部分, 想这样:
const e = 2.71828 // (approximately)
小数点前面或后面的数字都可能被省略(例如 .707 或 1.). 很小或很大的数最好用科学计数法书写, 通过e或E来指定指数部分:
const Avogadro = 6.02214129e23
const Planck = 6.62606957e-34
用 Printf 函数的 %g 参数打印浮点数, 将采用紧凑的表示形式打印, 并提供足够的精度, 但是对应表格的数据, 使用 %e (带指数) 或 %f 的形式打印可能更合适. 所有的这三个打印形式都可以指定打印的宽度和控制打印精度.
for x := 0; x < 8; x++ {
fmt.Printf("x = %d e^x = %8.3f\n", x, math.Exp(float64(x)))
}
上面代码打印e的幂, 打印精度是小数点后三个小数精度和8个字符宽度:
x = 0 e^x = 1.000
x = 1 e^x = 2.718
x = 2 e^x = 7.389
x = 3 e^x = 20.086
x = 4 e^x = 54.598
x = 5 e^x = 148.413
x = 6 e^x = 403.429
x = 7 e^x = 1096.633
math 包中除了提供大量常用的数学函数外, 还提供了IEEE754标准中特殊数值的创建和测试: 正无穷大和负无穷大, 分别用于表示太大溢出的数字和除零的结果; 还有 NaN 非数, 一般用于表示无效的除法操作结果 0/0 或 Sqrt(-1).
var z float64
fmt.Println(z, -z, 1/z, -1/z, z/z) // "0 -0 +Inf -Inf NaN"
函数 math.IsNaN 用于测试一个数是否是非数 NaN, math.NaN 则返回非数对应的值. 虽然可以用 math.NaN 来表示一个非法的结果, 但是测试一个结果是否是非数 NaN 则是充满风险, 因为 NaN 和任何数都是不相等的:
nan := math.NaN()
fmt.Println(nan == nan, nan < nan, nan > nan) // "false false false"
如果一个函数返回的浮点数结果可能失败, 最好的做法是用单独的标志报告失败, 像这样:
func compute() (value float64, ok bool) {
// ...
if failed {
return 0, false
}
return result, true
}
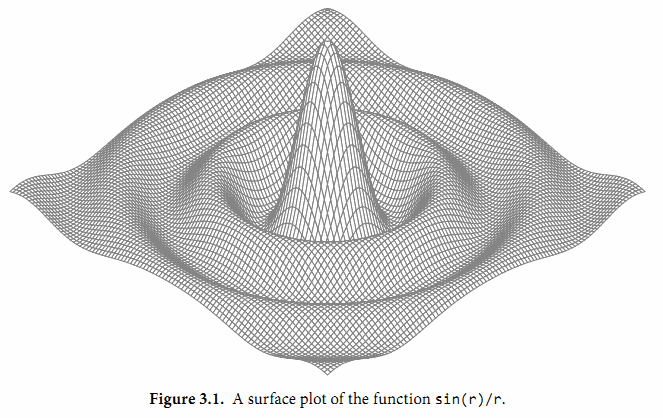
接下来的程序演示了浮点计算图形. 它是带有两个参数的 z = f(x, y) 函数的三维形式, 使用了可缩放矢量图形(SVG)格式输出, 一个用于矢量线绘制的XML标准. 图3.1显示了 sin(r)/r 函数的输出图形, 其中 r 是 sqrt(xx+yy).
gopl.io/ch3/surface
// Surface computes an SVG rendering of a 3-D surface function.
package main
import (
"fmt"
"math"
)
const (
width, height = 600, 320 // canvas size in pixels
cells = 100 // number of grid cells
xyrange = 30.0 // axis ranges (-xyrange..+xyrange)
xyscale = width / 2 / xyrange // pixels per x or y unit
zscale = height * 0.4 // pixels per z unit
angle = math.Pi / 6 // angle of x, y axes (=30°)
)
var sin30, cos30 = math.Sin(angle), math.Cos(angle) // sin(30°), cos(30°)
func main() {
fmt.Printf("<svg xmlns='http://www.w3.org/2000/svg' "+
"style='stroke: grey; fill: white; stroke-width: 0.7' "+
"width='%d' height='%d'>", width, height)
for i := 0; i < cells; i++ {
for j := 0; j < cells; j++ {
ax, ay := corner(i+1, j)
bx, by := corner(i, j)
cx, cy := corner(i, j+1)
dx, dy := corner(i+1, j+1)
fmt.Printf("<polygon points='%g,%g %g,%g %g,%g %g,%g'/>\n",
ax, ay, bx, by, cx, cy, dx, dy)
}
}
fmt.Println("</svg>")
}
func corner(i, j int) (float64, float64) {
// Find point (x,y) at corner of cell (i,j).
x := xyrange * (float64(i)/cells - 0.5)
y := xyrange * (float64(j)/cells - 0.5)
// Compute surface height z.
z := f(x, y)
// Project (x,y,z) isometrically onto 2-D SVG canvas (sx,sy).
sx := width/2 + (x-y)*cos30*xyscale
sy := height/2 + (x+y)*sin30*xyscale - z*zscale
return sx, sy
}
func f(x, y float64) float64 {
r := math.Hypot(x, y) // distance from (0,0)
return math.Sin(r) / r
}
要注意的是 corner 返回了两个结果, 对应 corner 的坐标参数.
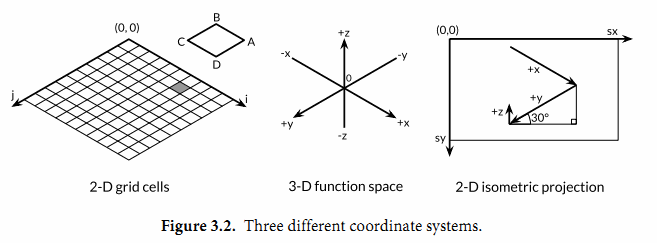
要解释程序是如何工作的需要了解基本的几何知识, 但是我们可以跳过几何原理, 因为程序的重点是演示浮点运算. 程序的本质是三个不同的坐标系中映射关系, 如图3.2所示. 第一个是 100x100 的二维网格, 对应整数整数坐标(i,j), 从远处的 (0, 0) 位置开始. 我们从远处像前面绘制, 因此远处先绘制的多边形有可能被前面后绘制的多边形覆盖.
第二个坐标系是一个三维的网格浮点坐标(x,y,z), 其中x和y是i和j的线性函数, 通过平移转换位center的中心, 然后用xyrange系数缩放. 高度z是函数f(x,y)的值.
第三个坐标系是一个二维的画布, 起点(0,0)在左上角. 画布中点的坐标用(sx, sy)表示. 我们使用等角投影将三维点
(x,y,z) 投影到二维的画布中. 画布中从远处到右边的点对应较大的x值和较大的y值. 并且画布中x和y值越大, 则对应的z值越小. x和y的垂直和水平缩放系数来自30度角的正弦和余弦值. z的缩放系数0.4, 是一个任意选择的参数.
对于二维网格中的每一个单位, main函数计算单元的四个顶点在画布中对应多边形ABCD的顶点, 其中B对应(i,j)顶点位置, A, C, 和 D是相邻的顶点, 然后输出SVG的绘制指令.
练习3.1: 如果 f 函数返回的是无限制的 float64 值, 那么SVG文件可能输出无效的多边形元素(虽然许多SVG渲染器会妥善处理这类问题). 修改程序跳过无效的多边形.
练习3.2: 试验math包中其他函数的渲染图形. 你是否能输出一个egg box, moguls, 或 a saddle 图案?
**练习3.3:**根据高度给每个多边形上色, 那样峰值部将是红色(#ff0000), 谷部将是蓝色(#0000ff).
3.4: 参考1.7节Lissajous例子的函数, 构造一个web服务器, 用于计算函数曲面然后返回SVG数据给客户端. 服务器必须设置 Content-Type 头部:
w.Header().Set("Content-Type", "image/svg+xml")
(这一步在Lissajous例子中不是必须的, 因为服务器使用标准的PNG图像格式, 可以根据前面的512个字节自动输出对应的头部.) 允许客户端通过HTTP请求参数设置高度, 宽度, 和颜色等参数.