9.7 KiB
| comments |
|---|
| true |
空间复杂度
「空间复杂度 Space Complexity」统计 算法使用内存空间随着数据量变大时的增长趋势 。这个概念与时间复杂度很类似。
算法相关空间
算法运行中,使用的内存空间主要有以下几种:
- 「输入空间」用于存储算法的输入数据;
- 「暂存空间」用于存储算法运行中的变量、对象、函数上下文等数据;
- 「输出空间」用于存储算法的输出数据;
!!! tip
通常情况下,空间复杂度统计范围是「暂存空间」+「输出空间」。
暂存空间可分为三个部分:
- 「暂存数据」用于保存算法运行中的各种 常量、变量、对象 等。
- 「栈帧空间」用于保存调用函数的上下文数据。系统每次调用函数都会在栈的顶部创建一个栈帧,函数返回时,栈帧空间会被释放。
- 「指令空间」用于保存编译后的程序指令,在实际统计中一般忽略不计。
Fig. 算法使用的相关空间
=== "Java"
```java title=""
/* 类 */
class Node {
int val;
Node next;
Node(int x) { val = x; }
}
/* 函数(或称方法) */
int function() {
// do something...
return 0;
}
int algorithm(int n) { // 输入数据
final int a = 0; // 暂存数据(常量)
int b = 0; // 暂存数据(变量)
Node node = new Node(0); // 暂存数据(对象)
int c = function(); // 栈帧空间(调用函数)
return a + b + c; // 输出数据
}
```
=== "C++"
```cpp title=""
```
=== "Python"
```python title=""
```
推算方法
空间复杂度的推算方法和时间复杂度总体类似,只是从统计 “计算操作数量” 变为统计 “使用空间大小” 。与时间复杂度不同的是,我们一般只关注「最差空间复杂度」。这是因为内存空间是一个硬性要求,我们必须保证在所有输入数据下都有足够的内存空间预留。
最差空间复杂度中的 “最差” 有两层含义,分别为输入数据的最差分布、算法运行中的最差时间点。
- 以最差输入数据为准。 当
n < 10时,空间复杂度为O(1);但是当n > 10时,初始化的数组nums使用O(n)空间;因此最差空间复杂度为O(n); - 以算法运行过程中的峰值内存为准。 程序在执行最后一行之前,使用
O(1)空间;当初始化数组nums时,程序使用O(n)空间;因此最差空间复杂度为O(n);
=== "Java"
```java title=""
void algorithm(int n) {
int a = 0; // O(1)
int[] b = new int[10000]; // O(1)
if (n > 10)
int[] nums = new int[n]; // O(n)
}
```
=== "C++"
```cpp title=""
```
=== "Python"
```python title=""
```
在递归函数中,需要注意统计栈帧空间。 例如函数 loop(),在循环中调用了 n 次 function() ,每轮中的 function() 都返回并释放了栈帧空间,因此空间复杂度仍为 O(1) 。而递归函数 recur() 在运行中会同时存在 n 个未返回的 recur() ,从而使用 O(n) 的栈帧空间。
=== "Java"
```java title=""
int function() {
// do something
return 0;
}
/* 循环 */
void loop(int n) {
for (int i = 0; i < n; i++) {
function();
}
}
/* 递归 */
void recur(int n) {
if (n == 1) return;
return recur(n - 1);
}
```
=== "C++"
```cpp title=""
```
=== "Python"
```python title=""
```
常见类型
设输入数据大小为 n ,常见的空间复杂度类型有(从低到高排列)
\begin{aligned}
O(1) < O(\log n) < O(n) < O(n^2) < O(2^n) \newline
\text{常数阶} < \text{对数阶} < \text{线性阶} < \text{平方阶} < \text{指数阶}
\end{aligned}
Fig. 空间复杂度的常见类型
!!! tip
部分示例代码需要一些前置知识,包括数组、链表、二叉树、递归算法等。如果遇到看不懂的地方无需担心,可以在学习完后面章节后再来复习,现阶段先聚焦在理解时间复杂度含义和推算方法上。
常数阶 O(1)
常数阶常见于数量与输入数据大小 n 无关的常量、变量、对象。
需要注意的是,在循环中初始化变量或调用函数而占用的内存,在进入下一循环后就会被释放,即不会累积占用空间,空间复杂度仍为 O(1) 。
=== "Java"
```java title="space_complexity_types.java"
/* 常数阶 */
void constant(int n) {
// 常量、变量、对象占用 O(1) 空间
final int a = 0;
int b = 0;
int[] nums = new int[10000];
ListNode node = new ListNode(0);
// 循环中的变量占用 O(1) 空间
for (int i = 0; i < n; i++) {
int c = 0;
}
// 循环中的函数占用 O(1) 空间
for (int i = 0; i < n; i++) {
function();
}
}
```
=== "C++"
```cpp title="space_complexity_types.cpp"
```
=== "Python"
```python title="space_complexity_types.py"
```
线性阶 O(n)
线性阶常见于元素数量与 n 成正比的数组、链表、栈、队列等。
=== "Java"
```java title="space_complexity_types.java"
/* 线性阶 */
void linear(int n) {
// 长度为 n 的数组占用 O(n) 空间
int[] nums = new int[n];
// 长度为 n 的列表占用 O(n) 空间
List<ListNode> nodes = new ArrayList<>();
for (int i = 0; i < n; i++) {
nodes.add(new ListNode(i));
}
// 长度为 n 的哈希表占用 O(n) 空间
Map<Integer, String> map = new HashMap<>();
for (int i = 0; i < n; i++) {
map.put(i, String.valueOf(i));
}
}
```
=== "C++"
```cpp title="space_complexity_types.cpp"
```
=== "Python"
```python title="space_complexity_types.py"
```
以下递归函数会同时存在 n 个未返回的 algorithm() 函数,使用 O(n) 大小的栈帧空间。
=== "Java"
```java title="space_complexity_types.java"
/* 线性阶(递归实现) */
void linearRecur(int n) {
System.out.println("递归 n = " + n);
if (n == 1) return;
linearRecur(n - 1);
}
```
=== "C++"
```cpp title="space_complexity_types.cpp"
```
=== "Python"
```python title="space_complexity_types.py"
```
Fig. 递归函数产生的线性阶空间复杂度
平方阶 O(n^2)
平方阶常见于元素数量与 n 成平方关系的矩阵、图。
=== "Java"
```java title="space_complexity_types.java"
/* 平方阶 */
void quadratic(int n) {
// 矩阵占用 O(n^2) 空间
int numMatrix[][] = new int[n][n];
// 二维列表占用 O(n^2) 空间
List<List<Integer>> numList = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<Integer> tmp = new ArrayList<>();
for (int j = 0; j < n; j++) {
tmp.add(0);
}
numList.add(tmp);
}
}
```
=== "C++"
```cpp title="space_complexity_types.cpp"
```
=== "Python"
```python title="space_complexity_types.py"
```
在以下递归函数中,同时存在 n 个未返回的 algorihtm() ,并且每个函数中都初始化了一个数组,长度分别为 n, n-1, n-2, ..., 2, 1 ,平均长度为 \frac{n}{2} ,因此总体使用 O(n^2) 空间。
=== "Java"
```java title="space_complexity_types.java"
/* 平方阶(递归实现) */
int quadraticRecur(int n) {
if (n <= 0) return 0;
int[] nums = new int[n];
System.out.println("递归 n = " + n + " 中的 nums 长度 = " + nums.length);
return quadraticRecur(n - 1);
}
```
=== "C++"
```cpp title="space_complexity_types.cpp"
```
=== "Python"
```python title="space_complexity_types.py"
```
Fig. 递归函数产生的平方阶空间复杂度
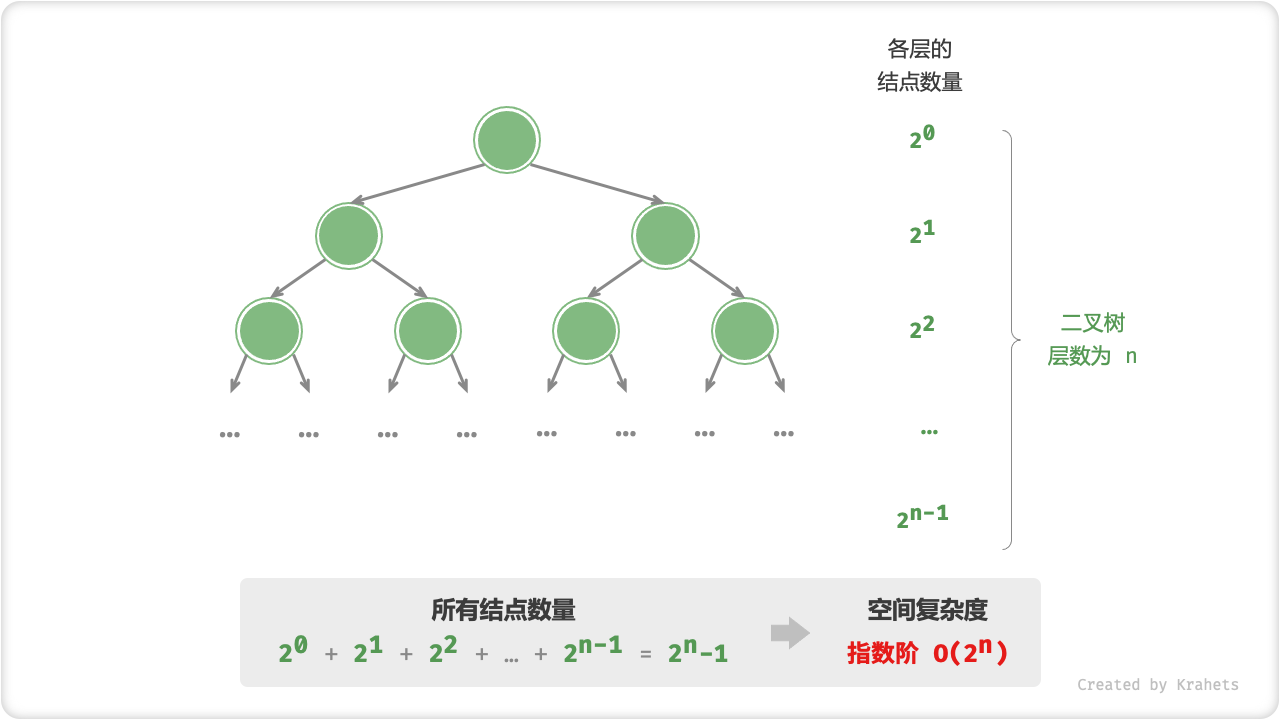
指数阶 O(2^n)
指数阶常见于二叉树。高度为 n 的「满二叉树」的结点数量为 2^n - 1 ,使用 O(2^n) 空间。
=== "Java"
```java title="space_complexity_types.java"
/* 指数阶(建立满二叉树) */
TreeNode buildTree(int n) {
if (n == 0) return null;
TreeNode root = new TreeNode(0);
root.left = buildTree(n - 1);
root.right = buildTree(n - 1);
return root;
}
```
=== "C++"
```cpp title="space_complexity_types.cpp"
```
=== "Python"
```python title="space_complexity_types.py"
```
Fig. 满二叉树下的指数阶空间复杂度
对数阶 O(\log n)
对数阶常见于分治算法、数据类型转换等。
例如「归并排序」,长度为 n 的数组可以形成高度为 \log n 的递归树,因此空间复杂度为 O(\log n) 。
再例如「数字转化为字符串」,输入任意正整数 n ,它的位数为 \log_{10} n ,即对应字符串长度为 \log_{10} n ,因此空间复杂度为 O(\log_{10} n) = O(\log n) 。