链接

README.md

@@ -50,7 +50,7 @@
 
 我把我之前学习算法时，**对我帮助很大的算法书籍，谷歌大神的刷题笔记，面经等整理在了云盘**，需要进阶的同学，可以自己下载，比较适合有一定基础的同学。
 
->  **[下载地址](https://wwr.lanzous.com/iSGhjox0yne)**
+>  **[下载地址](https://wwr.lanzoux.com/iSGhjox0yne)**
 
 想要手机阅读的大佬，可以来我的[公众号：袁厨的算法小屋](https://cdn.jsdelivr.net/gh/tan45du/test@master/微信图片_20210320152235.wp1ysdbibsw.png)进行阅读，两个平台同步更新，另外想要和题友们一起刷题**的同学可以来我的小屋，**点击**刷题小队**进入，另外群里老哥还会不定期发布内推消息，面经等，需要的可以进一下,不过来的时候**记得备注**，希望这个群能对你们有一丢丢帮助吧，一起加油。
 

animation-simulation/二叉树/二叉树的前序遍历(栈).md

@@ -0,0 +1,75 @@
+我们之前说了二叉树基础及二叉的几种遍历方式及练习题，今天我们来看一下二叉树的前序遍历非递归实现。
+
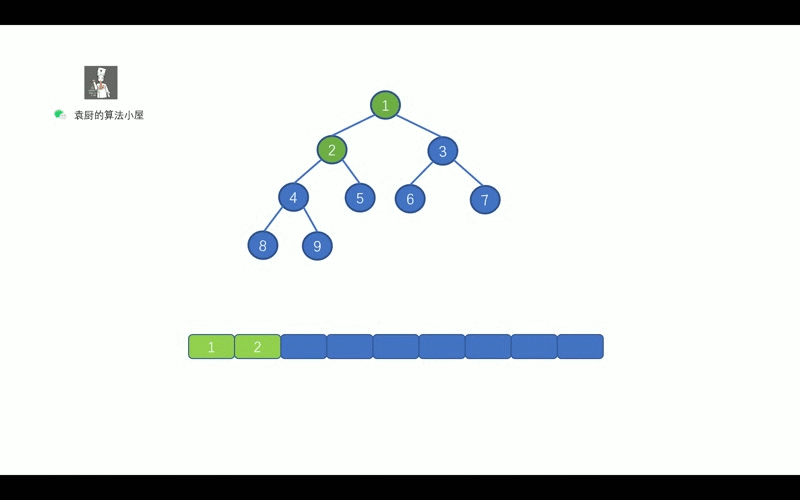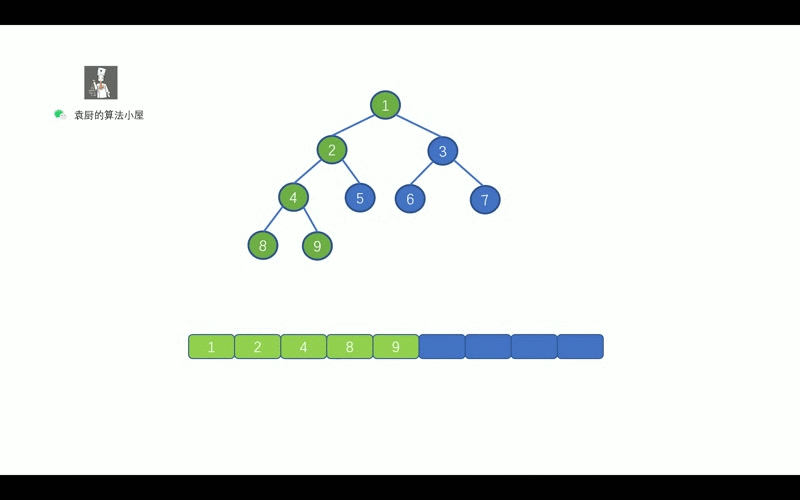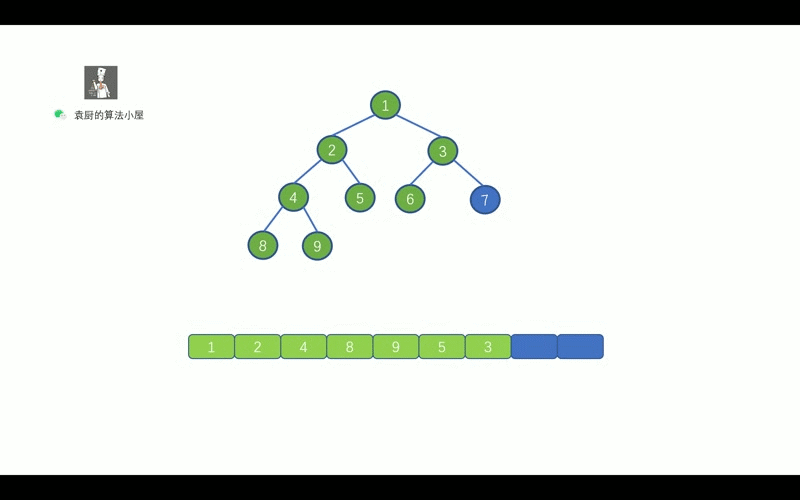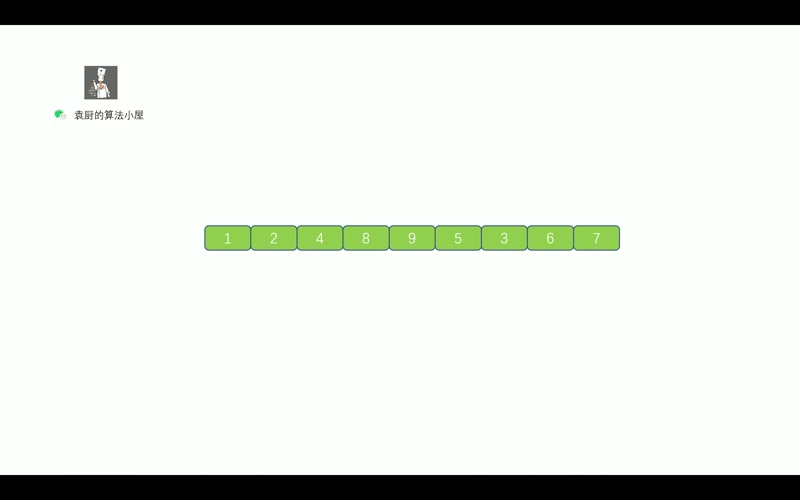
+前序遍历的顺序是, 对于树中的某节点,`先遍历该节点,然后再遍历其左子树,最后遍历其右子树`.
+
+我们先来通过下面这个动画复习一下二叉树的前序遍历。
+
+![前序遍历](https://img-blog.csdnimg.cn/20210504155755565.gif)
+
+### 迭代
+
+我们试想一下，之前我们借助队列帮我们实现二叉树的层序遍历，
+
+那么可不可以，也借助数据结构，帮助我们实现二叉树的前序遍历。
+
+见下图
+
+![image](https://cdn.jsdelivr.net/gh/tan45du/test@master/image.622242fm7dc0.png)
+
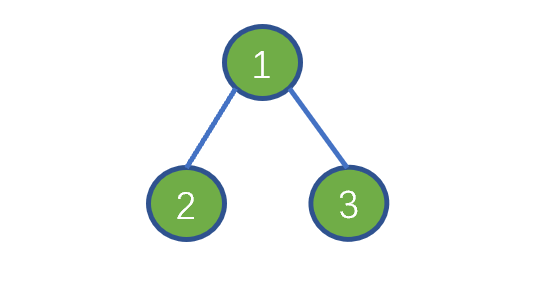
+假设我们的二叉树为 [1,2,3]。我们需要对其进行前序遍历。其遍历顺序为
+
+当前节点 1，左孩子 2，右孩子 3。
+
+这里可不可以用栈，帮我们完成前序遍历呢？
+
+> 栈和队列的那些事
+
+我们都知道栈的特性是先进后出，我们借助栈来帮助我们完成前序遍历的时候。
+
+则需要注意的一点是，我们应该先将右子节点入栈，再将左子节点入栈。
+
+这样出栈时，则会先出左节点，再出右子节点，则能够完成树的前序遍历。
+
+见下图。
+
+![](https://img-blog.csdnimg.cn/20210512205822221.gif)
+
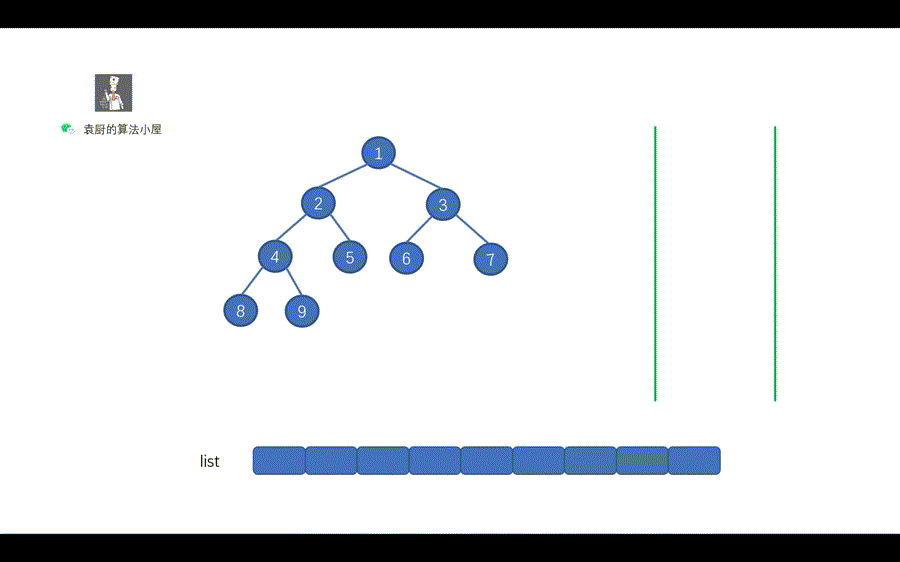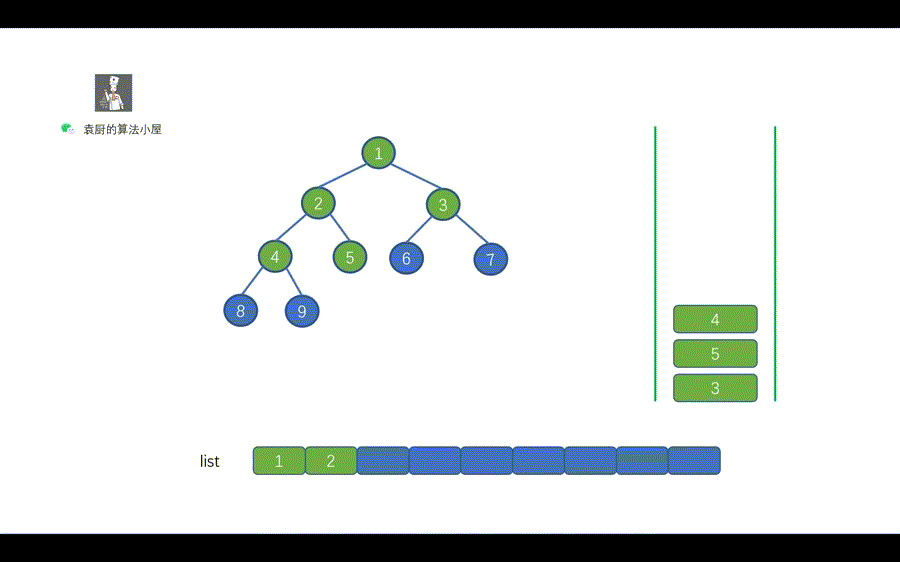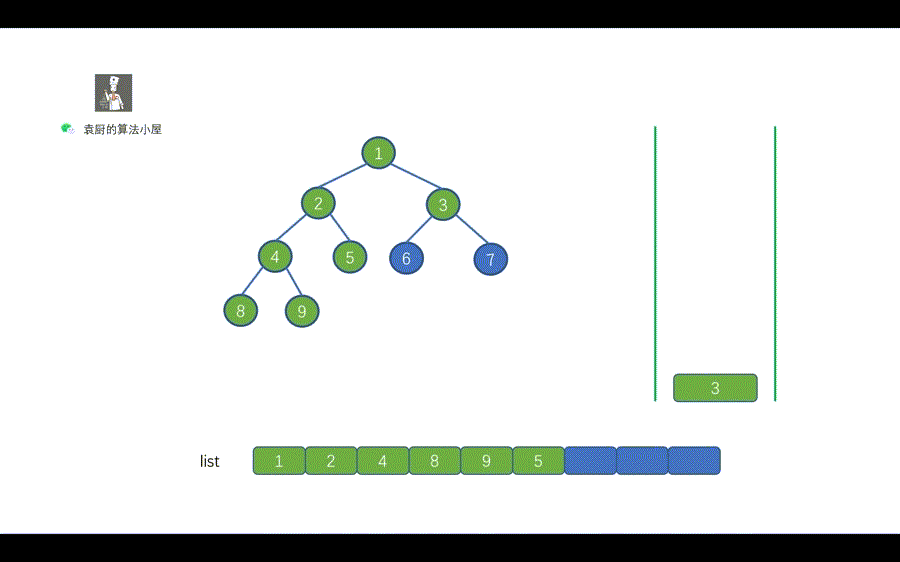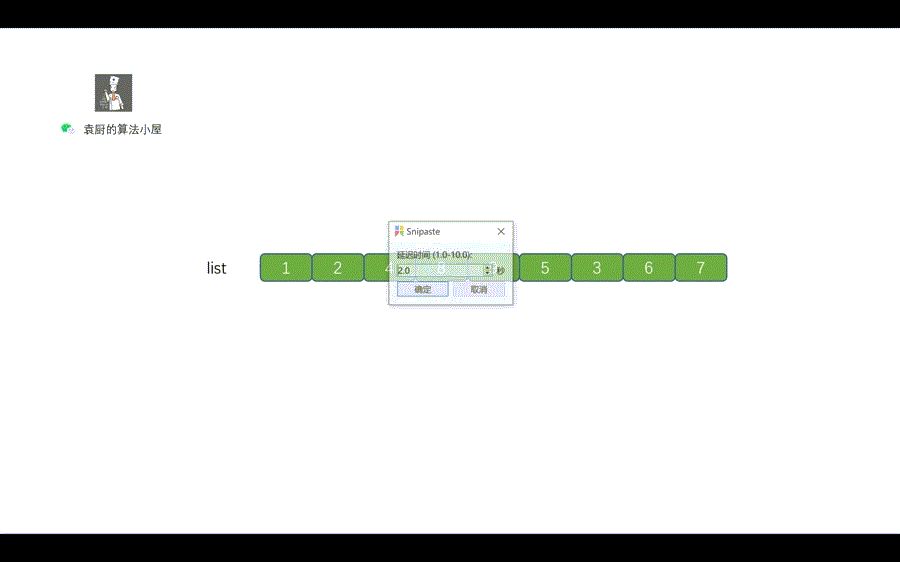
+我们用一句话对上图进行总结，当栈不为空时，栈顶元素出栈，如果其右孩子不为空，则右孩子入栈，其左孩子不为空，则左孩子入栈。还有一点需要注意的是，我们和层序遍历一样，需要先将 root 节点进行入栈，然后再执行 while 循环。
+
+看到这里你已经能够自己编写出代码了，不信你去试试。
+
+时间复杂度：O(n)  需要对所有节点遍历一次
+
+空间复杂度：O(n)  栈的开销，平均为 O(logn)  最快情况，即斜二叉树时为  O(n)
+
+**参考代码**
+
+```java
+class Solution {
+    public List<Integer> preorderTraversal(TreeNode root) {
+        List<Integer> list = new ArrayList<>();
+        Stack<TreeNode> stack = new Stack<>();
+        if (root == null)  return list;   
+        stack.push(root);
+        while (!stack.isEmpty()) {
+            TreeNode temp = stack.pop();        
+            if (temp.right != null) {
+                stack.push(temp.right);
+            }
+            if (temp.left != null) {
+                stack.push(temp.left);
+            }
+            //这里也可以放到前面
+            list.add(temp.val);
+        }
+        return list;
+    }
+}
+```
+
+### Morris
+
+Morris 遍历利用树的左右孩子为空（大量空闲指针），实现空间开销的极限缩减。这个遍历方法，稍微难理解一些，不过结合动图，也就一目了然啦，各位系好安全带，我们要发车啦。
+
+
+